جواب فصل 2 عددهای حقیقی ریاضی نهم
تعداد بازدید : 3.13Mپاسخ به تمامی سوالات فصل عددهای حقیقی - حل المسائل فصل 2 عددهای حقیقی - گام به گام 1401 کتاب ریاضی نهم - گام به گام کتاب ریاضی نهم مطابق با آخرین تغییرات کتب درسی
فعّالیت صفحه 19 درس عددهای حقیقی ریاضی نهم
پاسخ فعّالیت صفحه 19 درس 2
جواب فعّالیت صفحه 19 درس 2 ریاضی نهم
1 در فصل گذشته با نمایش های مختلفِ مجموعه های اعداد آشنا شدید. عبارت های زیر را مانند نمونه کامل کنید:
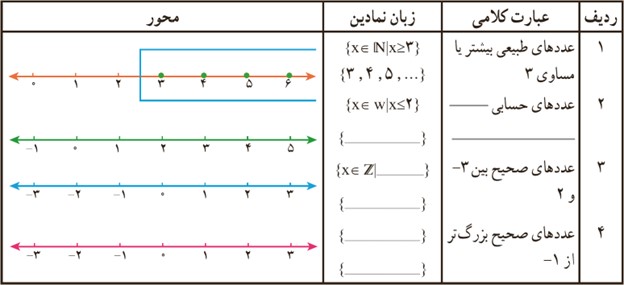
نامساوی \(x \ge 3\) برای کدام یک از عددهای زیر درست است؟
1 , 2 , 3 , 4 , 5
در مورد محدودیت ها و مزایا و معایب هرکدام از روش های نمایش مجموعه در کلاس گفت و گو کنید.
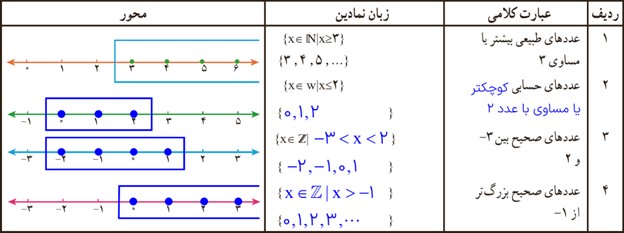
اعداد 3 ، 4 و 5 بزرگتر مساوی 3 هستند.
2 می خواهیم بین \(\frac{1}{2}\) و \(\frac{1}{3}\) چند کسر بنویسیم. روش های مختلفی را که چهار دانش آموز نوشته اند، بررسی و کامل کنید؛ راه حل هر کدام را توضیح دهید.

الف با یکی از روش ها توضیح دهید که چرا بین دو کسر می توان به هر تعداد، کسر پیدا کرد.
ب آیا مجموعهٔ عددهای گویا را می توان با نوشتن عضوها نشان داد؟ چرا؟
ج آیا می توان مجموعهٔ عددهای گویا را با محور اعداد نمایش داد؟
د عددهای گویا را به زبان نمادین معرفی کنید.
\(\left\{ {\frac{a}{b}|\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \right\}\)
روش مریم
1 ابتدا هر دو کسر را هم مخرج کرده و سپس اعداد \(\frac{1}{2} = \frac{3}{6}\) و \(\frac{1}{3} = \frac{2}{6}\) را روی محور مشخص کرده است.
2 برای بدست آوردن یک عدد بین این دو عدد هر قسمت را به دو قسمت مساوی تقسیم کرده، لذا یک واحد به دوازده قسمت مساوی تقسیم می شود بنابراین \(\frac{1}{2} = \frac{3}{6} = \frac{6}{{12}}\) و \(\frac{1}{3} = \frac{2}{6} = \frac{4}{{12}}\) می باشد و کسر \(\frac{5}{{12}}\) طبق شکل بین این دو عدد قرار می گیرد.
3 در این مرحله به جای تقسیم هر کدام از قسمت های کوچک به دو قسمت مساوی، هر کدام از آن ها را به 3 قسمت مساوی تقسیم می کند، لذا واحد به 18 قسمت مساوی تقسیم می شود بنابراین \(\frac{1}{2} = \frac{9}{{18}}\) و \(\frac{1}{3} = \frac{6}{{18}}\) می باشد و دو کسر \(\frac{7}{{18}}\) و \(\frac{8}{{18}}\) بین این دو عدد قرار می گیرد.
روش بهار
بهار دقیقا کار مریم را انجام داده است ولی محور رسم نکرده است. روش مریم مفهومی تر ولی روش بهار سریع تر می باشد، می توانیم بگوییم روش بهار نتیجه روش مریم می باشد.
روش مهناز
مهناز پس از مشخص کردن جای دو عدد روی محور از خاصیت میانگین دو عدد کمک گرفته است:
\(a < \frac{{a + b}}{2} < b\)
میانگین دو عدد \(\frac{1}{2}\) و \(\frac{1}{3}\) برابر \(\frac{5}{{12}}\) پس داریم:
\(\frac{1}{3} < \frac{5}{{12}} < \frac{1}{2}\)
در مرحله ی دوم ابتدا میانگین \(\frac{1}{3}\) و \(\frac{5}{{12}}\) و سپس میانگین \(\frac{1}{2}\) و \(\frac{5}{{12}}\) را بدست اورده است.
روش عطیه
عطیه هم دقیقا از روش مهناز استفاده کرده است، فقط محور رسم نکرده است.
الف
روش مریم
مریم می تواند یک واحد را به تعداد زیادی قسمت مساوی تقسیم کند و تعداد زیادی کسر بین این دو عدد بنویسد، اگر هر قسمت را به 100 قسمت مساوی تقسیم کند 99 عدد گویا بین این دو کسر می تواند بنویسد:
\(\begin{array}{l}\frac{1}{2} = \frac{3}{6} = \frac{{300}}{{600}}\quad ,\quad \frac{1}{3} = \frac{2}{6} = \frac{{200}}{{600}}\\\\\frac{1}{3} < \frac{{201}}{{600}}\,,\,\frac{{202}}{{600}}\,,\,\frac{{203}}{{600}}\,,\, \cdots \,,\,\frac{{299}}{{600}} < \frac{1}{2}\end{array}\)
اگر هر قسمت را به 1000 قسمت مساوی تقسیم کند 999 عدد گویا بین این دو کسر می تواند بنویسد:
\(\begin{array}{l}\frac{1}{2} = \frac{3}{6} = \frac{{3000}}{{6000}}\quad ,\quad \frac{1}{3} = \frac{2}{6} = \frac{{2000}}{{6000}}\\\\\frac{1}{3} < \frac{{2001}}{{6000}}\,,\,\frac{{2002}}{{6000}}\,,\,\frac{{2003}}{{6000}}\,,\, \cdots \,,\,\frac{{2999}}{{6000}} < \frac{1}{2}\end{array}\)
در روش مهناز نیز می توانیم به دفعات زیادی میانگین دو عدد را محاسبه کنیم
نتیجه: بین دو عدد گویا بی شمار عدد گویا وجود دارد
ب
خیر؛ چون بین دو عدد گویا بی شمار عدد گویا وجود دارد.
ج
خیر؛ بی شمار عدد گویا وجود دارد.
د
\(\left\{ {\frac{a}{b}|a\,,\,b \in \mathbb{Z}\,,\,b \ne 0\,} \right\}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
کار در کلاس صفحه 20 درس عددهای حقیقی ریاضی نهم
پاسخ کار در کلاس صفحه 20 درس 2
جواب کار در کلاس صفحه 20 درس 2 ریاضی نهم
1 بین \(\frac{2}{5}\) و \(\frac{3}{4}\) سه کسر پیدا کنید؛ روش خود را توضیح دهید.
\(\begin{array}{l}\frac{2}{5} = \frac{8}{{20}}\,\,\,,\,\,\,\frac{3}{4}\, = \frac{{15}}{{20}}\\\\ \Rightarrow \frac{2}{5} = \frac{8}{{20}} < \frac{9}{{20}}\,,\,\frac{{10}}{{20}}\,,\, \cdots \,,\,\frac{{14}}{{20}} < \frac{{15}}{{20}} = \frac{3}{4}\end{array}\)
دو کسر را هم مخرج می کنیم و بین \(\frac{8}{{20}}\) و \(\frac{{15}}{{20}}\) کسرهای \(\frac{{14}}{{20}}\,,\, \cdots \,,\,\frac{{10}}{{20}}\,,\,\frac{9}{{20}}\) را می نویسیم.
2 بین \( - \frac{1}{2}\) و 1- دو کسر پیدا کنید؛ روش خود را توضیح دهید.
\(\begin{array}{l} - 1 = - \frac{2}{2} = - \frac{{2 \times 3}}{{2 \times 3}} = - \frac{6}{6}\\\\ - \frac{1}{2} = - \frac{{1 \times 3}}{{2 \times 3}} = - \frac{3}{6}\\\\ \Rightarrow - 1 = - \frac{6}{6} < - \frac{5}{6}\,,\, - \frac{4}{6} < - \frac{3}{6} = - \frac{1}{2}\end{array}\)
گام به گام کتاب های پایه نهم
گام به گام جامع کتاب ریاضی نهم
گام به گام جامع کتاب علوم تجربی نهم
گام به گام جامع کتاب مطالعات اجتماعی نهم
گام به گام جامع کتاب عربی نهم
گام به گام جامع کتاب فارسی نهم
گام به گام جامع کتاب نگارش نهم
گام به گام جامع کتاب زبان انگلیسی نهم
گام به گام جامع کتاب کتاب کار انگلیسی نهم
گام به گام جامع کتاب آمادگی دفاعی نهم
گام به گام جامع کتاب پیام های آسمانی نهم
گام به گام جامع کتاب آموزش قرآن نهم
گام به گام جامع کتاب کار و فناوری نهم
گام به گام جامع کتاب تربیت دینی نهم
فعّالیت صفحه 20 درس عددهای حقیقی ریاضی نهم
پاسخ فعّالیت صفحه 20 درس 2
جواب فعّالیت صفحه 20 درس 2 ریاضی نهم
1 می خواهیم کسرهای \(\frac{3}{5}\) و \(\frac{5}{6}\) و \(\frac{7}{8}\) و \(\frac{5}{9}\) را به ترتیب از کوچک به بزرگ بنویسیم. روش های مختلفی را که دانش آموزان به کار برده اند، با هم مقایسه کنید؛ هر کدام را توضیح دهید و در صورت لزوم کامل کنید.
روش شاهد: شاهد به صورت تقریبی کسرهای \(\frac{3}{5}\) و \(\frac{5}{6}\) را روی محور مشخص کرده است. آیا به نظر شما استفاده از این روش برای نمایش دو کسر دیگر مناسب است؟
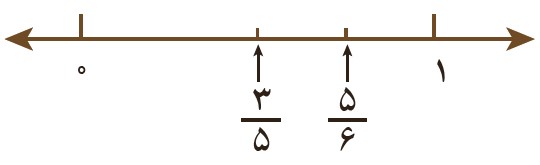
روش مرتضی: مرتضی مخرج مشترک کسرها را پیدا کرد و با هم مخرج کردن کسرها، آنها را مقایسه می کند. توضیح دهید که عدد 360 چگونه به دست می آید. کار مرتضی را کامل کنید:
\(\begin{array}{l}\frac{5}{9} = \frac{{}}{{360}}\\\\\frac{7}{8} = \frac{{\,\,\,\,\,\,\,\,\,}}{{}}\\\\\frac{5}{6} = \frac{{\,\,\,\,\,\,\,\,\,}}{{}}\\\\\frac{3}{5} = \frac{{\,\,\,\,\,\,\,\,\,}}{{}}\end{array}\)
روش مجید: مجید به کمک ماشین حساب، نمایش اعشاری هر کسر را تا دو رقم اعشار نوشت. شما کار او را کامل، و کسرها را مقایسه کنید:
\(\begin{array}{l}\frac{5}{9} \simeq 0/55\\\\\frac{7}{8} \simeq \\\\\frac{5}{6} \simeq \\\\\frac{3}{5} = \end{array}\)
در مورد روش های مختلف و ویژگی های هر کدام در کلاس گفت و گو کنید.
روش شاهد:
خیر
روش مرتضی:
\(\begin{array}{l}\frac{5}{9} = \frac{{200}}{{360}}\\\\\frac{7}{8} = \frac{{315}}{{360}}\\\\\frac{5}{6} = \frac{{300}}{{360}}\\\\\frac{3}{5} = \frac{{216}}{{360}}\end{array}\)
روش مجید:
\(\begin{array}{l}\frac{5}{9} \simeq 0/55\\\\\frac{7}{8} \simeq 0/87\\\\\frac{5}{6} \simeq 0/82\\\\\frac{3}{5} = 0/6\end{array}\)
برای مقایسه ی اعداد گویا با مخرج های مساوی و کوچک استفاده از محور روش مناسبی است. در صورتی که مخرج ها بزرگ باشد تقسیم یک واحد به قسمت های مساوی کار دشوار و حتی در خیلی موارد غیر ممکن است. لذا برای این سوال روش شاهد روش مناسبی نیست.
یکی از روش های مناسب برای مقایسه کسر ها هم مخرج کردن آن ها می باشد ولی این روش نیز به نوبه ی خود محدودیت هایی دارد و در صورتی که مخرج کسرها بزرگ باشد بدست آوردن «ک.م.م» آن ها بسیار وقت گیر است
مجید از ابزار استفاده کرده است و ابتدا صورت را بر مخرج تقسیم کرده و نماد اعشاری آن ها را بدست آورده و سپس آن ها را با هم مقایسه کرده، استفاده از ماشین حساب در زندگی روزمره و کسر های واقعی بسیار مناسب تر از دو روش بالا می باشد
این روش هم محدودیت هایی دارد؛ چون ممکن است ماشین حساب نداشته باشیم.
نتیجه: برای شروع کار روش شاهد مناسب ترین روش است و در انتها روش مجید در صورت داشتن ماشین حساب بسیار مناسب تر است.
2 با استفاده از تقسیم، نمایش اعشاری کسرهای زیر را بنویسید:
\(\begin{array}{l}\frac{3}{8} \simeq \\\\\frac{1}{3} \simeq \\\\\frac{7}{6} \simeq \end{array}\)
الف بین نمایش اعشاری این کسرها چه تفاوتی هست؟

\(\begin{array}{l}\frac{3}{8} \simeq 0/38\\\\\frac{1}{3} \simeq 0/33\\\\\frac{7}{6} \simeq 1/17\end{array}\)
الف
تفاوت اصلی این است که برخی از این کسرها نمایشی مختوم (پایانپذیر) دارند و برخی دیگر نمایشی متناوب (تکرارشونده).
اعشار مختوم: نمایش اعشاری کسر \(\frac{3}{8}\) یک عدد اعشاری مختوم است. یعنی تقسیم صورت بر مخرج پایان میپذیرد و تعداد ارقام اعشاری آن محدود است.
اعشار متناوب: نمایش اعشاری کسرهای \(\frac{1}{3}\) و \(\frac{7}{6}\) متناوب است. یعنی در تقسیم، یک یا چند رقم به طور نامحدود تکرار میشوند.
\(0/\bar 3\) یک اعشار متناوب ساده است، زیرا بخش تکرارشونده بلافاصله بعد از ممیز شروع میشود.
\(1/1\bar 6\) یک اعشار متناوب مرکب است، زیرا بین ممیز و بخش تکرارشونده (۶)، یک بخش غیرتکراری (۱) وجود دارد.
کار در کلاس صفحه 22 درس عددهای حقیقی ریاضی نهم
پاسخ کار در کلاس صفحه 22 درس 2
جواب کار در کلاس صفحه 22 درس 2 ریاضی نهم
نمایش اعشاری هر یک از کسرهای زیر را بنویسید:
\(\begin{array}{l}\frac{5}{{11}} = \\\\\frac{7}{9} = \\\\\frac{5}{6} = \\\\\frac{7}{{22}} = \\\\\frac{3}{{20}} = \\\\\frac{5}{{16}} = \end{array}\)
اگر به نمایش اعشاری کسرهای بالا دقت کنید، خواهید دید که فقط کسرهایی نمایش اعشاری مختوم دارند که )پس از ساده شدن( مخرج آنها شمارنده اوّلی به جز 2 و 5 ندارد.
\(\begin{array}{l}\frac{5}{{11}} = 0/4\bar 5\\\\\frac{7}{9} = 0/\bar 7\\\\\frac{5}{6} = 0/8\bar 3\\\\\frac{7}{{22}} = 0/3\overline {18} \\\\\frac{3}{{20}} = 0/15\\\\\frac{5}{{16}} = 0/3125\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
تمرین صفحه 22 درس عددهای حقیقی ریاضی نهم
پاسخ تمرین صفحه 22 درس 2
جواب تمرین صفحه 22 درس 2 ریاضی نهم
1 حاصل عبارت های زیر را به دست آورید و تا حد امکان ساده کنید:
\(\begin{array}{l}( - 2\frac{5}{6} + 3\frac{1}{2}) \div ( - 1 - \frac{1}{9})\\\\\frac{{1 - \frac{1}{2} + \frac{3}{4}}}{{\frac{5}{{10}} - \frac{3}{4} - \frac{1}{2}}} \div 5\frac{1}{3}\\\\ - \frac{1}{2} + \frac{{ - 5}}{6} \div \frac{7}{3} \times \frac{7}{5} + \frac{2}{3}\\\\\frac{1}{{ - 1 - \frac{1}{{ - 1 - \frac{1}{3}}}}}\end{array}\)
\(\begin{array}{l}( - 2\frac{5}{6} + 3\frac{1}{2}) \div ( - 1 - \frac{1}{9}):\\\\\left\{ \begin{array}{l} - 2\frac{5}{6} + 3\frac{1}{2} = - \frac{{17}}{6} + \frac{7}{2} = \\\\ - \frac{{17}}{6} + \frac{{21}}{6} = \frac{{ - 17 + 21}}{6} = \frac{4}{6} = \frac{2}{3}\end{array} \right.\\\\\left\{ { - 1 - \frac{1}{9} = - \frac{9}{9} - \frac{1}{9} = - \frac{{10}}{9}} \right.\\\\ \Rightarrow ( - 2\frac{5}{6} + 3\frac{1}{2}) \div ( - 1 - \frac{1}{9}) = \\\\\frac{2}{3} \div ( - \frac{{10}}{9}) = \frac{2}{3} \times ( - \frac{9}{{10}}) = - \frac{3}{5} = - 0/6\end{array}\)
\(\begin{array}{l}\frac{{1 - \frac{1}{2} + \frac{3}{4}}}{{\frac{5}{{10}} - \frac{3}{4} - \frac{1}{2}}} \div 5\frac{1}{3}:\\\\\left\{ {1 - \frac{1}{2} + \frac{3}{4} = \frac{4}{4} - \frac{2}{4} + \frac{3}{4} = \frac{5}{4}} \right.\\\\\left\{ {\frac{5}{{10}} - \frac{3}{4} - \frac{1}{2} = \frac{1}{2} - \frac{3}{4} - \frac{1}{2} = - \frac{3}{4}} \right.\\\\\left\{ {\frac{{1 - \frac{1}{2} + \frac{3}{4}}}{{\frac{5}{{10}} - \frac{3}{4} - \frac{1}{2}}} = \frac{{\frac{5}{4}}}{{ - \frac{3}{4}}} = - \frac{{5 \times 4}}{{4 \times 3}} = - \frac{5}{3}} \right.\\\\ \Rightarrow \frac{{1 - \frac{1}{2} + \frac{3}{4}}}{{\frac{5}{{10}} - \frac{3}{4} - \frac{1}{2}}} \div 5\frac{1}{3} = - \frac{5}{3} \div 5\frac{1}{3} = \\\\ - \frac{5}{3} \div \frac{{16}}{3} = - \frac{5}{3} \times \frac{3}{{16}} = - \frac{5}{{16}} = - 0/3125\end{array}\)
\(\begin{array}{l} - \frac{1}{2} + \frac{{ - 5}}{6} \div \frac{7}{3} \times \frac{7}{5} + \frac{2}{3}:\\\\\left\{ {\frac{{ - 5}}{6} \div \frac{7}{3} = \frac{{ - 5}}{6} \times \frac{3}{7} = - \frac{5}{{14}}} \right.\\\\\left\{ {\frac{{ - 5}}{6} \div \frac{7}{3} \times \frac{7}{5} = - \frac{5}{{14}} \times \frac{7}{5} = - \frac{1}{2}} \right.\\\\ \Rightarrow - \frac{1}{2} + \frac{{ - 5}}{6} \div \frac{7}{3} \times \frac{7}{5} + \frac{2}{3} = \\\\ - \frac{1}{2} - \frac{1}{2} + \frac{2}{3} = - 1 + \frac{2}{3} = \\\\ - \frac{3}{3} + \frac{2}{3} = - \frac{1}{3}\end{array}\)
\(\begin{array}{l}\frac{1}{{ - 1 - \frac{1}{{ - 1 - \frac{1}{3}}}}}:\\\\\left\{ { - 1 - \frac{1}{3} = - \frac{3}{3} - \frac{1}{3} = - \frac{4}{3}} \right.\\\\\left\{ \begin{array}{l} - 1 - \frac{1}{{ - 1 - \frac{1}{3}}} = - 1 - \frac{1}{{ - \frac{4}{3}}} = \\\\ - 1 + \frac{3}{4} = - \frac{4}{4} + \frac{3}{4} = - \frac{1}{4}\end{array} \right.\\\\ \Rightarrow \frac{1}{{ - 1 - \frac{1}{{ - 1 - \frac{1}{3}}}}} = \frac{1}{{ - \frac{1}{4}}} = - 4\end{array}\)
ضرب و تقسیم بر جمع و تفریق اولویت دارد ولی چون تقسیم ابتدا آمده مرحله اول تقسیم و سپس ضرب و در مرحله ی سوم جمع و تفریق را باید انجام دهیم.
2 عددهای زیر را از کوچک به بزرگ مرتب کنید:
\(\frac{7}{8}\;,\; - \frac{2}{3}\;,\;\frac{3}{4}\;,\;2\;,\; - 3\frac{5}{6}\) الف
\(\frac{{16}}{7}\;,\; - \frac{3}{4}\;,\;2/75\;,\; - \frac{5}{6}\;,\;4\frac{3}{5}\;,\;\frac{{56}}{{13}}\) ب
الف
\(\begin{array}{l}\frac{7}{8}\;,\; - \frac{2}{3}\;,\;\frac{3}{4}\;,\;2\;,\; - 3\frac{5}{6}\\\\ \Rightarrow \left[ {8\,,\,6\,,\,4\,,\,3\,,\,1} \right] = 24\\\\\left\{ \begin{array}{l}\frac{7}{8} = \frac{{21}}{{24}}\\\\ - \frac{2}{3} = - \frac{{16}}{{24}}\\\\\frac{3}{4} = \frac{{18}}{{24}}\\\\2 = \frac{{48}}{{24}}\\\\ - 3\frac{5}{6} = - \frac{{23}}{6} = - \frac{{92}}{{24}}\end{array} \right.\\\\ \Rightarrow - \frac{{92}}{{24}} < - \frac{{16}}{{24}} < \frac{{18}}{{24}} < \frac{{21}}{{24}} < \frac{{48}}{{24}}\\\\ \Rightarrow - 3\frac{5}{6} < - \frac{2}{3} < \frac{3}{4} < \frac{7}{8} < 2\\\\ \Rightarrow - 3\frac{5}{6}\,,\, - \frac{2}{3}\,,\,\frac{3}{4}\,,\,\frac{7}{8}\,,\,2\end{array}\)
ب
\(\begin{array}{l}\frac{{16}}{7}\;,\; - \frac{3}{4}\;,\;2/75\;,\; - \frac{5}{6}\;,\;4\frac{3}{5}\;,\;\frac{{56}}{{13}}\\\\\left\{ \begin{array}{l}\frac{{16}}{7} = 2\frac{2}{7} \simeq 2/28\\\\ - \frac{3}{4} = - 0/75\\\\ - \frac{5}{6} \simeq - 0/83\\\\4\frac{3}{5} = 4/6\\\\\frac{{56}}{{13}} = 4\frac{4}{{13}} \simeq 4/3\end{array} \right.\\\\ \Rightarrow - 0/83 < - 0/75 < 2/75 < 2/28 < 4/3 < 4/6\\\\ \Rightarrow - \frac{5}{6} < - \frac{3}{4} < 2/75 < \frac{{16}}{7} < \frac{{56}}{{13}} < 4\frac{3}{5}\\\\ \Rightarrow - \frac{5}{6}\,,\, - \frac{3}{4}\,,\,2/75\,,\,\frac{{16}}{7}\,,\,\frac{{56}}{{13}}\,,\,4\frac{3}{5}\end{array}\)
3 بین هر دو کسر، سه کسر بنویسید.
\(\frac{{10}}{{11}}\;,\;\frac{{12}}{{13}}\) الف
\(0\;,\; - \frac{1}{3}\) ب
الف
\(\begin{array}{l}\frac{{10}}{{11}} = \frac{{10 \times 13}}{{11 \times 13}} = \frac{{130}}{{143}} = \frac{{130 \times 10}}{{143 \times 10}} = \frac{{1300}}{{1430}}\\\\\frac{{12}}{{13}} = \frac{{12 \times 11}}{{13 \times 11}} = \frac{{132}}{{143}}\frac{{132 \times 10}}{{143 \times 10}} = \frac{{1320}}{{1430}}\\\\\frac{{10}}{{11}} = \frac{{1300}}{{1430}} < \frac{{1301}}{{1430}}\,,\,\frac{{1302}}{{1430}}\,,\,\frac{{1303}}{{1430}} < \frac{{1320}}{{1430}} = \frac{{12}}{{13}}\\\\ \Rightarrow \frac{{1301}}{{1430}}\,,\,\frac{{1302}}{{1430}}\,,\,\frac{{1303}}{{1430}}\end{array}\)
ب
\(\begin{array}{l} - \frac{1}{3} = - \frac{{1 \times 10}}{{3 \times 10}} = - \frac{{10}}{{30}}\\\\0 = \frac{{0 \times 10}}{{1 \times 10}} = \frac{0}{{10}} = 0\\\\ - \frac{1}{3} = - \frac{{10}}{{30}} < - \frac{9}{{30}}\,,\, - \frac{8}{{30}}\,,\, - \frac{7}{{30}} < 0\\\\ \Rightarrow - \frac{9}{{30}} = - \frac{3}{{10}}\,,\, - \frac{8}{{30}} = - \frac{4}{{15}}\,,\, - \frac{7}{{30}}\\\\ \Rightarrow - \frac{3}{{10}}\,,\, - \frac{4}{{15}}\,,\, - \frac{7}{{30}}\end{array}\)
گام به گام کتاب های پایه نهم
گام به گام جامع کتاب ریاضی نهم
گام به گام جامع کتاب علوم تجربی نهم
گام به گام جامع کتاب مطالعات اجتماعی نهم
گام به گام جامع کتاب عربی نهم
گام به گام جامع کتاب فارسی نهم
گام به گام جامع کتاب نگارش نهم
گام به گام جامع کتاب زبان انگلیسی نهم
گام به گام جامع کتاب کتاب کار انگلیسی نهم
گام به گام جامع کتاب آمادگی دفاعی نهم
گام به گام جامع کتاب پیام های آسمانی نهم
گام به گام جامع کتاب آموزش قرآن نهم
گام به گام جامع کتاب کار و فناوری نهم
گام به گام جامع کتاب تربیت دینی نهم
فعّالیت صفحه 23 درس عددهای حقیقی ریاضی نهم
پاسخ فعّالیت صفحه 23 درس 2
جواب فعّالیت صفحه 23 درس 2 ریاضی نهم
1 پنج عدد بین 1 و 2 معرفی کنید و آنها را روی محور نمایش دهید.


2 با توجه به اینکه مقدار تقریبی \(\sqrt 2 \) مساوی 1/4 است، آن را روی محور نشان دهید.
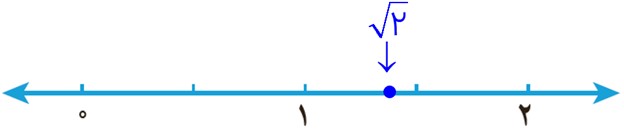
3 معلّم از دانش آموزان خواست با ماشین حساب، مقدار تقریبی عدد \(\sqrt 2 \) را بنویسند. با توجه به اینکه دانش آموزان از ماشین حساب های مختلف استفاده می کردند، تعداد رقم هایی که نوشته بودند، متفاوت بود. سه نمونه از صفحهٔ نمایش ماشین حساب ها را در زیر می بینید. با توجه به آنها به سؤال های زیر پاسخ دهید:

الف چرا در ماشین حساب 8 رقمی، رقم آخر با رقم مشابه در ماشین حساب 12 رقمی تفاوت دارد؟
ب چرا این تفاوت در ماشین حساب های 10 رقمی و 12 رقمی دیده نمی شود؟
پ با توجه به عددی که ماشین حساب 12 رقمی نشان می دهد، آیا تناوب )تکرار منظم( در رقم های اعشاری دیده می شود؟
ت مقدار تقریبی \(\sqrt 2 \)، تا 15 رقم اعشار محاسبه، و در زیر نوشته شده است:
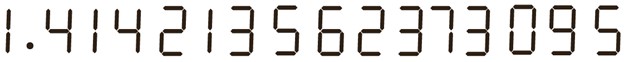
آیا در 15 رقم نشان داده شده برای \(\sqrt 2 \)، تناوبی می بینید؟
الف
دلیل این تفاوت، عملیات گرد کردن در ماشین حساب ۸ رقمی است. مقدار دقیق رادیکال ۲ با ارقام بیشتر برابر 1/41421356… است. ماشین حساب ۸ رقمی برای نمایش عدد تا ۷ رقم اعشار، به رقم هشتم (که ۶ است) نگاه میکند. چون این رقم بزرگتر از ۵ است، رقم هفتم (۵) را به ۶ گرد میکند و نتیجه را 1/4142136 نشان میدهد.
ب
این تفاوت بین ماشین حسابهای ۱۰ و ۱۲ رقمی دیده نمیشود، زیرا در آنجا رقم مسئول گرد کردن کمتر از ۵ است. برای مثال، ماشین حساب ۱۰ رقمی (که ۸ رقم اعشار نشان میدهد) به نهمین رقم اعشار (که ۲ است) نگاه میکند و چون ۲ کمتر از ۵ است، رقم قبلی را تغییر نمیدهد.
پ
خیر، با توجه به ارقام نمایش داده شده در ماشین حساب ۱۲ رقمی (1/414213562…)، هیچ تناوب یا تکرار منظمی در ارقام اعشاری دیده نمیشود.
ت
خیر، در ۱۵ رقم اعشاری نمایش داده شده برای رادیکال ۲ نیز هیچ تناوبی وجود ندارد. این ویژگی اصلی اعداد گنگ (اصم) مانند رادیکال ۲ است که نمایش اعشاری آنها نه تنها پایان ندارد، بلکه هیچگاه به یک الگوی تکرارشونده نیز نمیرسد.
کار در کلاس صفحه 24 درس عددهای حقیقی ریاضی نهم
پاسخ کار در کلاس صفحه 24 درس 2
جواب کار در کلاس صفحه 24 درس 2 ریاضی نهم
کدام عبارت، درست و کدام عبارت، نادرست است؟
\(\begin{array}{l}Q \cap Q' \in \emptyset \\\\N \subseteq Q'\\\\Z \subseteq Q\\\\Z \subseteq Q'\end{array}\)
عبارت های \(Q \cap Q' \in \emptyset \) و \(Z \subseteq Q\) درست هستند و عبارت های \(N \subseteq Q'\) و \(Z \subseteq Q'\) درست نیستند.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
فعّالیت صفحه 24 درس عددهای حقیقی ریاضی نهم
پاسخ فعّالیت صفحه 24 درس 2
جواب فعّالیت صفحه 24 درس 2 ریاضی نهم
الف بین دو عدد 1 و 2 چند عدد گویا می توان نوشت؟
ب اگر این عددها را روی محور نمایش دهیم، متناظر با این عددها، چند نقطه روی محورپ می توان پیدا کرد؟
ج روی محور نقطهٔ نمایش \(\sqrt 2 \) را پیدا کنید.

د اگر نقاطی را رنگ کنیم که عددی گویا را نمایش می دهد، آیا همهٔ نقاط پاره خط AB رنگ می شود؟ آیا \(\sqrt 2 \) نیز رنگ می شود؟ آیا این نقاط، که هر کدام نمایش یک عددگویا است، یک پاره خط به وجود می آورد؟ چرا؟
الف
بین هر دو عدد گویا بیشمار عدد گویا وجود دارد
\(\begin{array}{l}1 < \cdots \,,\,1\frac{1}{6}\,,\,1\frac{1}{5}\,,\,1\frac{1}{4}\,,\,1\frac{1}{3}\,,\,1\frac{1}{2} < 2\\\\ \Rightarrow 1 < \cdots \,,\,\frac{7}{6}\,,\,\frac{6}{5}\,,\,\frac{5}{4}\,,\,\frac{4}{3}\,,\,\frac{3}{2} < 2\end{array}\)
ب
متناظر با هر عدد فقط یک نقطه وجود دارد در کل بی شمار نقطه داریم.
ج
\(\begin{array}{l}O{C^2} = O{A^2} + A{C^2}\\\\ \Rightarrow O{C^2} = {1^2} + {1^2} = 1 + 1 = 2\\\\ \Rightarrow OC = \sqrt 2 \\\\1 < \sqrt 2 < 1/5\end{array}\)
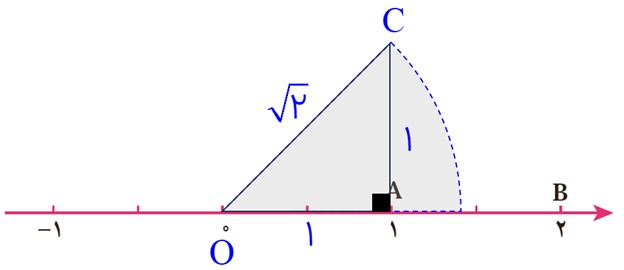
د
بین دو عدد 1 و 2 بیشمار عدد گنگ و بی شمار عدد گویا وجود دارد. و بین هر دو عدد گویا بی شمار عدد گنگ وجود دارد. وقتی نقاط متناظر با اعداد گویا بین 1 و2 را رنگ می کنیم، نقاط متناظر با اعداد گنگ رنگ نشده باقی می ماند، در نتیجه این نقاط نمی توانند پاره خط بوجود آورند.
بین هر دو عدد گویا بی شمار عدد گویا وجود دارد
بین هر دو عدد گویا بی شمار عدد گنگ وجود دارد
بین دو عدد گنگ بی شمار عدد گنگ وجود دارد
بین هذ دو عدد گنگ بی شمار عدد گویا وجود دارد
گام به گام کتاب های پایه نهم
گام به گام جامع کتاب ریاضی نهم
گام به گام جامع کتاب علوم تجربی نهم
گام به گام جامع کتاب مطالعات اجتماعی نهم
گام به گام جامع کتاب عربی نهم
گام به گام جامع کتاب فارسی نهم
گام به گام جامع کتاب نگارش نهم
گام به گام جامع کتاب زبان انگلیسی نهم
گام به گام جامع کتاب کتاب کار انگلیسی نهم
گام به گام جامع کتاب آمادگی دفاعی نهم
گام به گام جامع کتاب پیام های آسمانی نهم
گام به گام جامع کتاب آموزش قرآن نهم
گام به گام جامع کتاب کار و فناوری نهم
گام به گام جامع کتاب تربیت دینی نهم
کار در کلاس صفحه 25 درس عددهای حقیقی ریاضی نهم
پاسخ کار در کلاس صفحه 25 درس 2
جواب کار در کلاس صفحه 25 درس 2 ریاضی نهم
1 بین \(\sqrt 5 \) و \(\sqrt {10} \) ، چهار عدد گنگ بنویسید.
برای پیدا کردن اعداد گنگ بین \(\sqrt 5 \) و \(\sqrt {10} \) ، کافی است اعدادی بین ۵ و ۱۰ انتخاب کنیم که جذر کامل نداشته باشند و سپس جذر آنها را بنویسیم. چهار نمونه عبارتند از:
\(\sqrt 6 \,,\,\sqrt 7 \,,\,\sqrt 8 \,,\,\sqrt {9/1} \)
2 بین دو عدد 2 و 3، چهار عدد گنگ بنویسید.
ابتدا اعداد ۲ و ۳ را به صورت رادیکالی مینویسیم: \(2 = \sqrt 4 \) و \(3 = \sqrt 9 \) حالا باید چهار عدد گنگ بین \(\sqrt 4 \) و \(\sqrt 9 \) پیدا کنیم. چهار نمونه عبارتند از:
\(\sqrt 5 \,,\,\sqrt 6 \,,\,\sqrt 7 \,,\,\sqrt 8 \)
3 الف مجموعۀ A به صورت \(A = \left\{ {x \subseteq Q|2 \le x \le 3} \right\}\) را در نظر بگیرید. آیا نمایش A به صورت زیر درست است؟

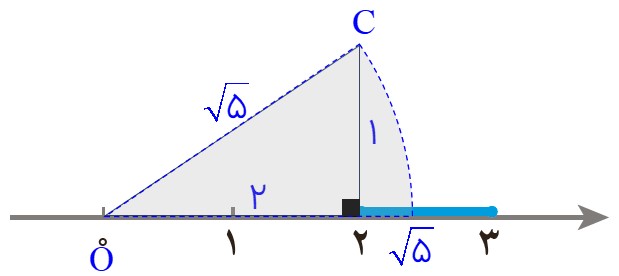
ب نقطهٔ نمایش \(\sqrt 5 \) را روی محور مشخص کنید.
الف
خیر، نمایش داده شده درست نیست.
دلیل: مجموعهٔ \(A = \left\{ {x \subseteq Q|2 \le x \le 3} \right\}\) شامل تمام اعداد گویا بین ۲ و ۳ است. اما خط ممتد و توپر روی محور، نمایشدهندهٔ تمام اعداد حقیقی (شامل گویا و گنگ) بین ۲ و ۳ است. از آنجایی که بین ۲ و ۳ اعداد گنگ بیشماری مانند \( \cdots \,,\,\sqrt 6 \,,\,\sqrt 5 \) وجود دارند که در مجموعه A نیستند، این نمایش صحیح نمیباشد.
ب
برای مشخص کردن \(\sqrt 5 \) روی محور، از قضیه فیثاغورس استفاده میکنیم:
1 یک مثلث قائمالزاویه روی محور اعداد رسم میکنیم که یک ضلع آن به طول ۲ واحد (از ۰ تا ۲) و ضلع دیگر آن به طول ۱ واحد (عمود بر محور) باشد.
2 طول وتر این مثلث برابر با \(\sqrt {{2^2} + {1^2}} = \sqrt {4 + 1} = \sqrt 5 \) خواهد بود.
3 با استفاده از پرگار، دهانه را به اندازه طول وتر باز کرده، سوزن آن را روی مبدأ (نقطه ۰) قرار میدهیم و یک کمان میزنیم تا محور اعداد را قطع کند. نقطهٔ برخورد، نمایش عدد \(\sqrt 5 \) است.
کار در کلاس صفحه 25 درس عددهای حقیقی ریاضی نهم
پاسخ کار در کلاس صفحه 25 درس 2
جواب کار در کلاس صفحه 25 درس 2 ریاضی نهم
1 داخل \(\bigcirc \) علامت \( \in \) یا \( \notin \) بگذارید:
\(\begin{array}{l}4\;\bigcirc \;Z\;\;\;\;\;\;\;\;\;\;\;0/2\;\bigcirc \;Q\\\\\sqrt {18} \;\bigcirc \;R\;\;\;\;\;\;\;\;\frac{{\sqrt 7 }}{{\sqrt 2 }}\;\bigcirc \;R\\\\ - 5\;\bigcirc \;R\;\;\;\;\;\;\;\;\; - \frac{7}{3}\;\bigcirc \;Z\\\\\sqrt {25} \;\bigcirc \;Q'\;\;\;\;\;\;\;\;\frac{0}{6}\;\bigcirc \;R\\\\\sqrt {3/5} \;\bigcirc \;Q'\;\;\;\;\;\sqrt {0/9} \;\bigcirc \;Q'\\\\\sqrt {0/09} \;\bigcirc \;Q\;\;\;\;\;\;\frac{9}{{ - 1}}\;\bigcirc \;Z\end{array}\)
\(\begin{array}{l}4\; \in \;Z\;\;\;\;\;\;\;\;\;\;\;0/2\; \in \;Q\\\\\sqrt {18} \; \in \;R\;\;\;\;\;\;\;\;\frac{{\sqrt 7 }}{{\sqrt 2 }}\; \in \;R\\\\ - 5\; \in \;R\;\;\;\;\;\;\;\;\; - \frac{7}{3}\;\not \in \;Z\\\\\sqrt {25} \;\not \in \;Q'\;\;\;\;\;\;\;\;\frac{0}{6}\; \in \;R\\\\\sqrt {3/5} \; \in \;Q'\;\;\;\;\;\sqrt {0/9} \; \in \;Q'\\\\\sqrt {0/09} \; \in \;Q\;\;\;\;\;\;\frac{9}{{ - 1}}\; \in \;Z\end{array}\)
2 مجموعه های سطراوّل را به مجموعهٔ مناسب در سطر دوم وصل کنید. هر مجموعه در سطر اوّل با یک مجموعه در سطر دوم مساوی است.
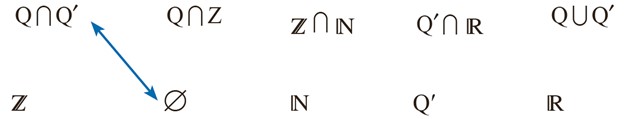

مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
فعّالیت صفحه 26 درس عددهای حقیقی ریاضی نهم
پاسخ فعّالیت صفحه 26 درس 2
جواب فعّالیت صفحه 26 درس 2 ریاضی نهم
با توجه به اینکه مجموعهٔ عددهای حقیقی تمام عددها را شامل می شود، مجموعه های زیر را مانند نمونه روی محور نشان دهید:

با توجه به مجموعهٔ A چرا نقطهٔ ٢ روی محور توپر و نقطهٔ ٣ روی محور توخالی است؟
\(\begin{array}{l}A = \left\{ {x \in R|2 \le x < 3} \right\}\\\\B = \left\{ {x \in R|x < - 2} \right\}\\\\C = \left\{ {x \in R| - 1 \le x \le 5} \right\}\\\\D = \left\{ {x \in R|x \ge 6} \right\}\end{array}\)
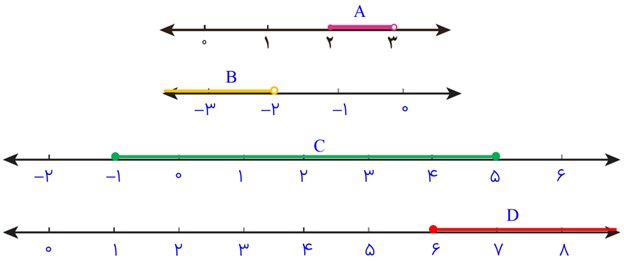
نامساوی x<3 به این معنی است که x باید از 3 کمتر باشد و مجموعه شامل عدد 3 می باشد و نامساوی \(2 \le x\) یعنی مجموعه شامل 2 و اعداد بزرگتر از آن می باشد.
گام به گام کتاب های پایه نهم
گام به گام جامع کتاب ریاضی نهم
گام به گام جامع کتاب علوم تجربی نهم
گام به گام جامع کتاب مطالعات اجتماعی نهم
گام به گام جامع کتاب عربی نهم
گام به گام جامع کتاب فارسی نهم
گام به گام جامع کتاب نگارش نهم
گام به گام جامع کتاب زبان انگلیسی نهم
گام به گام جامع کتاب کتاب کار انگلیسی نهم
گام به گام جامع کتاب آمادگی دفاعی نهم
گام به گام جامع کتاب پیام های آسمانی نهم
گام به گام جامع کتاب آموزش قرآن نهم
گام به گام جامع کتاب کار و فناوری نهم
گام به گام جامع کتاب تربیت دینی نهم
کار در کلاس صفحه 26 درس عددهای حقیقی ریاضی نهم
پاسخ کار در کلاس صفحه 26 درس 2
جواب کار در کلاس صفحه 26 درس 2 ریاضی نهم
1 مجموعه های زیر را روی محور نشان دهید و یا با توجه به محور، مجموعهٔ متناظر آن را بنویسید:

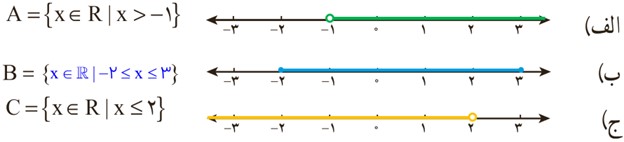
2 توجه به سه مجموعه A و B و C در سؤال ١ عبارات درست را با علامت P مشخص کنید:
\(\begin{array}{l}0/75 \in A\\\\0/252552555... \in B\\\\\sqrt {13} \in A\\\\\sqrt 7 \in C\\\\\sqrt 1 \in A\\\\ - 1000 \in C\end{array}\)
\(0/75 \in A\)
درست
\(0/252552555... \in B\)
درست
\(\sqrt {13} \in A\)
درست
\(\sqrt 7 \in C\)
نادرست
\(\sqrt 1 \in A\)
درست
\( - 1000 \in C\)
درست
3 کدام یک از مجموعه های زیر با مجموعهٔ نقاط روی شکل زیر، برابر است؟

الف \(\left\{ { - 1\,,\,0\,,\,1\,,\,2\,,\,3} \right\}\)
ب \(\left\{ {x \in R|x > - 2} \right\}\)
ج \(\left\{ {x \in R| - 2 < x < 3} \right\}\)
ج \(\left\{ {x \in R| - 2 < x < 3} \right\}\) ؛ یعنی تمام اعداد حقیقی بزرگتر از 2- و کوچکتر از 3.
تمرین صفحه 27 درس عددهای حقیقی ریاضی نهم
پاسخ تمرین صفحه 27 درس 2
جواب تمرین صفحه 27 درس 2 ریاضی نهم
1 با توجه به مجموعه های داده شده، سایر سطرها را مانند سطر اوّل کامل کنید:
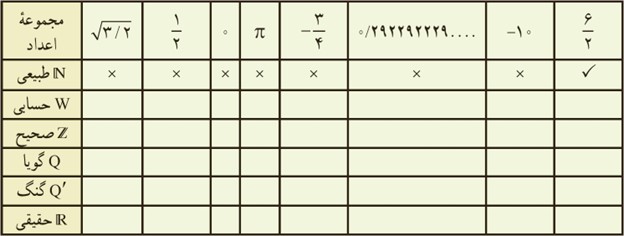
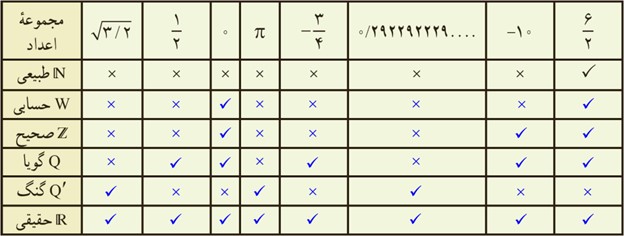
2 در هر یک از حالت های الف و ب تفاوت دو مجموعه را با ذکر دلیل بنویسید:
\(A = \left\{ {x \in R|1/5 < x < 5} \right\}\;\;\;,\;\;\;B = \left\{ {x \in Q|1/5 < x < 5} \right\}\) الف
\(C = \left\{ {4,5,6,7,8} \right\}\;\;,\;\;D = \left\{ {x \in R|3 < x < 9} \right\}\) ب
الف
مجموعه ی A شامل همه ی اعداد بین 1/5 و 5 است (اعداد گویا و گنگ) ولی مجموعه B فقط شامل اعداد گویای بین این دو عدد می باشد
ب
مجموعه ی D شامل تمام اعداد گویا و گنگ بین 3 و 9 می باشد ولی مجموعه ی C فقط شامل اعداد طبیعی بین 3 و 9 می باشد
3 طرف دوم تساوی های زیر را کامل کنید:
1 \(N \cup Z = \)
2 \(R - Q' = \)
3 \(Z \cap N = \)
4 \(R \cap Q' = \)
1 \(N \cup Z = Z\)
2 \(R - Q' = Q\)
3 \(Z \cap N = N\)
4 \(R \cap Q' = Q'\)
4 عدد \(1 + \sqrt 5 \) بین کدام دو عدد صحیح متوالی قرار دارد؟
\(\begin{array}{l}1 + \sqrt 5 :\\\\4 < 5 < 9 \Rightarrow \sqrt 4 < \sqrt 5 < \sqrt 9 \\\\ \Rightarrow 2 < \sqrt 5 < 3\\\\ \Rightarrow 1 + 2 < 1 + \sqrt 5 < 1 + 3\\\\ \Rightarrow 3 < 1 + \sqrt 5 < 4\end{array}\)
5 بین هر دو عدد، چهار عدد گنگ بنویسید:
الف-2 , 5
ب6 , 7
\(\sqrt 3 \;,\;6\) ج
\(\sqrt 2 \;,\;\sqrt {4/1} \) د
الف
\(\begin{array}{l}\left\{ \begin{array}{l} - 2 = - \sqrt 4 \\\\5 = \sqrt {25} \end{array} \right.\\\\ \Rightarrow - \sqrt 3 \,,\, - \sqrt 2 \,,\,\sqrt 2 \,,\,\sqrt 3 \end{array}\)
ب
\(\begin{array}{l}\left\{ \begin{array}{l}6 = \sqrt {36} \\\\7 = \sqrt {49} \end{array} \right.\\\\ \Rightarrow \sqrt {40} \,,\,\sqrt {42} \,,\,\sqrt {44} \,,\,\sqrt {46} \end{array}\)
ج
\(\begin{array}{l}\left\{ \begin{array}{l}\sqrt 3 \\\\6 = \sqrt {36} \end{array} \right.\\\\ \Rightarrow \sqrt 5 \,,\,\sqrt 6 \,,\,\sqrt 7 \,,\,\sqrt 8 \end{array}\)
د
\(\begin{array}{l}\left\{ \begin{array}{l}\sqrt 2 \\\\\sqrt {4/1} \end{array} \right.\\\\ \Rightarrow \sqrt {2/5} \,,\,\sqrt 3 \,,\,\sqrt {3/6} \,,\,\sqrt {3/9} \end{array}\)
6 عبارات درست را با P و عبارات نادرست را با × مشخص کنید. برای عبارات درست مثال بزنید.
١ عددی وجود دارد که صحیح و گویا باشد.
٢ عددی وجود دارد که گویا و گنگ باشد.
٣ عددی وجود دارد که حقیقی و گنگ باشد.
٤ عددی وجود دارد که حقیقی و طبیعی باشد.
عبارات صحیح از قرار زیر می باشند:
1 ، 3 و 4
مثال برای 1 : تمام اعداد صحیح گویا هستند.
مثال برای 3 : \(\sqrt 2 \) هم گنگ است و هم حقیقی.
مثال برای 4 : تمام اعداد طبیعی، حقیقی می باشند.
7 در نمایش اعشاری عدد \(\sqrt {10} \) و عدد \(\frac{3}{{11}}\) چه تفاوتی هست؟
در نمایش اعشاری \(\frac{3}{{11}}\) دوره تناوب وجود دارد و 27 تکرار می شود ولی در نمایش اعشاری \(\sqrt {10} \) دوره تناوب وجود ندارد.
\(\begin{array}{l}\frac{3}{{11}} = 0/27272727 \cdots = 0/\overline {27} \\\\\sqrt {10} = 3/1622776601683 \cdots \end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
فعّالیت صفحه 28 درس عددهای حقیقی ریاضی نهم
پاسخ فعّالیت صفحه 28 درس 2
جواب فعّالیت صفحه 28 درس 2 ریاضی نهم
1 با توجه به شکل، به سؤالات زیر پاسخ دهید:

الف نقاط A و B چه عددی را نمایش می دهد؟
ب فاصلهٔ نقطه A از O با طول پاره خط OA چقدر است؟
پ فاصلهٔ نقطه B از O با طول پاره خط OB چقدر است؟
می خواهیم نقاطی را روی محور بیابیم که فاصله آن از O برابر 2 باشد.
الف

ب
OA = 2
پ
OB = 2
2 نقطه C را روی محور نمایش دهید به طوری که طول OC برابر ٢ باشد؛ چند نقطه می توان یافت؟
دو نقطه:

گام به گام کتاب های پایه نهم
گام به گام جامع کتاب ریاضی نهم
گام به گام جامع کتاب علوم تجربی نهم
گام به گام جامع کتاب مطالعات اجتماعی نهم
گام به گام جامع کتاب عربی نهم
گام به گام جامع کتاب فارسی نهم
گام به گام جامع کتاب نگارش نهم
گام به گام جامع کتاب زبان انگلیسی نهم
گام به گام جامع کتاب کتاب کار انگلیسی نهم
گام به گام جامع کتاب آمادگی دفاعی نهم
گام به گام جامع کتاب پیام های آسمانی نهم
گام به گام جامع کتاب آموزش قرآن نهم
گام به گام جامع کتاب کار و فناوری نهم
گام به گام جامع کتاب تربیت دینی نهم
کار در کلاس صفحه 29 درس عددهای حقیقی ریاضی نهم
پاسخ کار در کلاس صفحه 29 درس 2
جواب کار در کلاس صفحه 29 درس 2 ریاضی نهم
1 جملات سمت راست را به عبارات مناسب در سمت چپ وصل کنید:
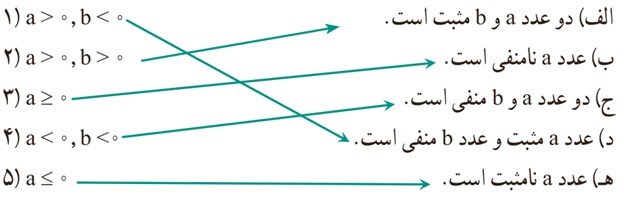
2 هر عبارت سمت راست، نتیجهٔ منطقی یک عبارت در سمت چپ است. عبارات مناسب را به هم وصل کنید:


3 هر عبارت سمت راست، نتیجهٔ منطقی یک عبارت در سمت چپ است. عبارات مناسب را به هم وصل کنید:


4 عبارات زیر را به زبان ریاضی بنویسید و برای هر کدام مثال بنویسید:
١ قدر مطلقِ حاصل ضربِ دو عدد، مساوی با حاصل ضرب قدر مطلقِ آنهاست.
٢ قدر مطلقِ مجموع دو عدد، از مجموع قدرمطلق های آن دو عدد، کوچک تر یا مساوی با آن است.
1
\(\begin{array}{l}\left| {ab} \right| = \left| a \right|\left| b \right|\\\\ \Rightarrow \left\{ \begin{array}{l}a = - 3\\\\b = - 2\end{array} \right.\\\\ \Rightarrow \left| {( - 3) \times ( - 2)} \right| = \left| { - 3} \right|\left| { - 2} \right|\\\\ \Rightarrow 6 = 6\end{array}\)
2
\(\begin{array}{l}\left| {a + b} \right| \le \left| a \right| + \left| b \right|\\\\ \Rightarrow \left\{ \begin{array}{l}a = - 15\\\\b = 20\end{array} \right.\\\\ \Rightarrow \left| { - 15 + 20} \right| \le \left| { - 15} \right| + \left| {20} \right|\\\\ \Rightarrow 5 \le 35\end{array}\)
فعّالیت صفحه 29 درس عددهای حقیقی ریاضی نهم
پاسخ فعّالیت صفحه 29 درس 2
جواب فعّالیت صفحه 29 درس 2 ریاضی نهم
مقدار تقریبی عددهای زیر تا یک رقم اعشار نوشته شده است:
\(\begin{array}{l}\sqrt 2 \simeq 1/4\;\;\;\;\;\;\;\sqrt 3 \simeq 1/7\\\\\sqrt 5 \simeq 2/2\;\;\;\;\;\;\;\sqrt 6 \simeq 2/4\\\\\sqrt 7 \simeq 2/6\;\;\;\;\;\;\;\sqrt 8 \simeq 2/8\end{array}\)
با توجه به مقادیر تقریبی صفحهٔ قبل، تساوی های زیر را مانند نمونه کامل کنید و دلیل خود را توضیح دهید:
\(\left| {1 - \sqrt 2 } \right| = - \left( {1 - \sqrt 2 } \right) = - 1 + \sqrt 2 = \sqrt 2 - 1\)
دلیل: \(\sqrt 2 \simeq 1/4\) پس \(1 - \sqrt 2 \) عددی منفی می شود:
1 \(\left| {2 - \sqrt 3 } \right| = \)
دلیل:
2 \(\left| {\sqrt 7 - \sqrt 8 } \right|\)
دلیل:
3 \(\left| {2\sqrt 5 - \sqrt 5 } \right| = \)
دلیل:
4 \(\left| { - 4 - \sqrt 3 } \right| = \)
دلیل:
1 \(\left| {2 - \sqrt 3 } \right| = 2 - \sqrt 3 \)
دلیل: \(\sqrt 3 \simeq 1/7\) ، پس \(2 - \sqrt 3 \) مثبت می شود.
2 \(\left| {\sqrt 7 - \sqrt 8 } \right| = \sqrt 8 - \sqrt 7 \)
دلیل: \(\sqrt 7 \simeq 2/6\) و \(\sqrt 8 \simeq 2/8\) ، پس \(\sqrt 7 - \sqrt 8 \) منفی می شود.
3 \(\left| {2\sqrt 5 - \sqrt 5 } \right| = \sqrt 5 \)
دلیل: \(\sqrt 5 \simeq 2/2\) و \(2\sqrt 5 \simeq 4/5\) ، پس \(2\sqrt 5 - \sqrt 5 \) مثبت می شود.
4 \(\left| { - 4 - \sqrt 3 } \right| = 4 + \sqrt 3 \)
دلیل: هر دو عدد 4- و \( - \sqrt 3 \) منفی هستند، پس \( - 4 - \sqrt 3 \) منفی می شود.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم
فعّالیت صفحه 30 درس عددهای حقیقی ریاضی نهم
پاسخ فعّالیت صفحه 30 درس 2
جواب فعّالیت صفحه 30 درس 2 ریاضی نهم
جدول زیر را کامل کنید:
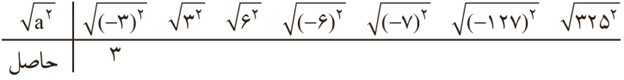
از فعالیت بالا چه نتیجه ای می گیرید؟
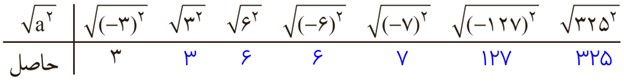
حاصل \(\sqrt {{a^2}} \) همیشه مثبت است.
گام به گام کتاب های پایه نهم
گام به گام جامع کتاب ریاضی نهم
گام به گام جامع کتاب علوم تجربی نهم
گام به گام جامع کتاب مطالعات اجتماعی نهم
گام به گام جامع کتاب عربی نهم
گام به گام جامع کتاب فارسی نهم
گام به گام جامع کتاب نگارش نهم
گام به گام جامع کتاب زبان انگلیسی نهم
گام به گام جامع کتاب کتاب کار انگلیسی نهم
گام به گام جامع کتاب آمادگی دفاعی نهم
گام به گام جامع کتاب پیام های آسمانی نهم
گام به گام جامع کتاب آموزش قرآن نهم
گام به گام جامع کتاب کار و فناوری نهم
گام به گام جامع کتاب تربیت دینی نهم
کار در کلاس صفحه 31 درس عددهای حقیقی ریاضی نهم
پاسخ کار در کلاس صفحه 31 درس 2
جواب کار در کلاس صفحه 31 درس 2 ریاضی نهم
1 عبارت های زیر را با هم مقایسه کنید:
\(\left| {{{\left( { - 7} \right)}^2}} \right|\;\bigcirc \;{\left| { - 7} \right|^2}\) الف
\(\left| { - 8 + 5} \right|\;\bigcirc \;\left| { - 8} \right| + \left| 5 \right|\) ب
\(\left| {3 - 9} \right|\;\bigcirc \;\left| 3 \right| - \left| 9 \right|\) ج
الف
\(\begin{array}{l}\left| {{{\left( { - 7} \right)}^2}} \right|\; = \left| {49} \right|\; = 49\\\\{\left| { - 7} \right|^2} = {(7)^2}\; = 49\\\\ \Rightarrow \left| {{{\left( { - 7} \right)}^2}} \right|\; = \;{\left| { - 7} \right|^2}\end{array}\)
ب
\(\begin{array}{l}\left| { - 8 + 5} \right| = \left| { - 3} \right| = 3\\\\\left| { - 8} \right| + \left| 5 \right| = 8 + 5 = 13\\\\ \Rightarrow \left| { - 8 + 5} \right|\; < \;\left| { - 8} \right| + \left| 5 \right|\end{array}\)
ج
\(\begin{array}{l}\left| {3 - 9} \right| = \left| { - 6} \right| = 6\\\\\left| 3 \right| - \left| 9 \right| = 3 - 9 = - 6\\\\ \Rightarrow \left| {3 - 9} \right|\; > \;\left| 3 \right| - \left| 9 \right|\end{array}\)
2 عبارات زیر را بدون استفاده از قدرمطلق بنویسید:
\(\begin{array}{l}\left| {\;0\;} \right| = \;\\\\\left| { - \frac{4}{3}} \right| = \\\\\left| {{7^3} - {7^4}} \right| = \\\\\left| {0/{2^5} - 0/{2^6}} \right| = \end{array}\)
\(\begin{array}{l}\left| {\;0\;} \right| = \;0\\\\\left| { - \frac{4}{3}} \right| = \frac{4}{3}\\\\\left| {{7^3} - {7^4}} \right| = - ({7^3} - {7^4}) = {7^4} - {7^3}\\\\\left| {0/{2^5} - 0/{2^6}} \right| = 0/{2^5} - 0/{2^6}\end{array}\)
3 حاصل عبارات زیر رابه دست آورید:
\(\sqrt {{{\left( { - 2595} \right)}^2}} = \) الف
ب \(\sqrt {{{\left( {1394} \right)}^2}} = \)
ج \(\sqrt {{{\left( { - 3 + \sqrt {10} } \right)}^2}} = \)
د \(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} = \)
الف
\(\sqrt {{{\left( { - 2595} \right)}^2}} = \left| { - 2595} \right| = 2595\)
ب
\(\sqrt {{{\left( {1394} \right)}^2}} = \left| {1394} \right| = 1394\)
ج
\(\sqrt {{{\left( { - 3 + \sqrt {10} } \right)}^2}} = \left| { - 3 + \sqrt {10} } \right| = \sqrt {10} - 3\)
د
\(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} = \left| {2 - \sqrt 5 } \right| = \sqrt 5 - 2\)
تمرین صفحه 31 درس عددهای حقیقی ریاضی نهم
پاسخ تمرین صفحه 31 درس 2
جواب تمرین صفحه 31 درس 2 ریاضی نهم
1 اگر \(c = 2\frac{1}{2}\;\;,\;\;b = - \frac{1}{4}\;\;,\,\;a = 0/25\) باشد، حاصل عبارت زیر را به دست آورید:
\(\left| {a + b} \right| + 2\left| {a - b - c} \right|\)
\(\begin{array}{l}\left| {a + b} \right| + 2\left| {a - b - c} \right| = \\\\\left| {0/25 - \frac{1}{4}} \right| + 2\left| {0/25 + \frac{1}{4} - 2\frac{1}{2}} \right| = \\\\\left| {\frac{1}{4} - \frac{1}{4}} \right| + 2\left| {\frac{1}{4} + \frac{1}{4} - 2\frac{1}{2}} \right| = \\\\0 + 2\left| {\frac{1}{2} - 2\frac{1}{2}} \right| = 2\left| { - 2} \right| = 2(2) = 4\end{array}\)
2 عبارات زیر را بدون استفاده از قدرمطلق بنویسید:
\(\left| { - 3\sqrt 5 } \right|\) الف
ب \(\left| {7 - 5\sqrt 3 } \right|\)
ج \(\left| {0 + \sqrt 5 } \right|\)
الف
\(\left| { - 3\sqrt 5 } \right| = - ( - 3\sqrt 5 ) = 3\sqrt 5 \)
ب
\(\begin{array}{l}\left| {7 - 5\sqrt 3 } \right| = \left| {\sqrt {49} - \sqrt {25 \times 3} } \right| = \\\\\left| {\sqrt {49} - \sqrt {75} } \right| = - (\sqrt {49} - \sqrt {75} ) = \\\\\sqrt {75} - \sqrt {49} = 5\sqrt 3 - 7\end{array}\)
ج
\(\left| {0 + \sqrt 5 } \right| = \left| {\sqrt 5 } \right| = \sqrt 5 \)
3 جای خالی را با عدد مناسب پر، و جواب هایتان را در کلاس با سایر دوستانتان مقایسه کنید:
\(\left| {5 - 12} \right| > 1 + \;\bigcirc \)
\(\begin{array}{l}\left| {5 - 12} \right| > 1 + \;\bigcirc \\\\ \Rightarrow \left| { - 7} \right| > 1 + \;\bigcirc \\\\ \Rightarrow 7 > 1 + \;\bigcirc \\\\ \Rightarrow 7 - 1 > 1 + \;\bigcirc - 1\\\\ \Rightarrow 6 > \;\bigcirc \end{array}\)
پس \(\bigcirc \) ، هر عدد کوچکتر از 6 می تواند باشد؛ مثل 5، 4، 2- و ...
4 مقدار عددی عبارت |a|+a را به ازای a=-2 ، a=0 و a=2 به دست آورید. آیا می توانید عددی حقیقی به جای a قرار دهید که حاصل |a|+a منفی باشد؟
\(\begin{array}{l}\left\{ \begin{array}{l}a = - 2\\\\\left| a \right| = \left| { - 2} \right| = 2\end{array} \right. \Rightarrow a + \left| a \right| = - 2 + 2 = 0\\\\\left\{ \begin{array}{l}a = 0\\\\\left| a \right| = \left| 0 \right| = 0\end{array} \right. \Rightarrow a + \left| a \right| = 0 + 0 = 0\\\\\left\{ \begin{array}{l}a = 2\\\\\left| a \right| = \left| 2 \right| = 2\end{array} \right. \Rightarrow a + \left| a \right| = 2 + 2 = 4\end{array}\)
خیر؛ به ازای هیچ یک از اعداد حقیقی، عبارت a+|a| منفی نخواهد شد.
5 با ارائهٔ یک مثال، نادرست بودن تساوی \(\sqrt {{a^2}} = a\) را نشان دهید.
\(\begin{array}{l}a = - 7\\\\\sqrt {{{( - 7)}^2}} = \sqrt {49} = 7 \ne - 7\end{array}\)
مثال فوق، یک مثال نقض برای تساوی \(\sqrt {{a^2}} = a\) می باشد.
6 حاصل عبارات روبه رو را به دست آورید:
\(\begin{array}{l}\sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} \\\\\sqrt {{{\left( {1 - \sqrt {10} } \right)}^2}} \end{array}\)
\(\begin{array}{l}\sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} = \left| {\sqrt 2 - 1} \right| = \sqrt 2 - 1\\\\\sqrt {{{\left( {1 - \sqrt {10} } \right)}^2}} = \left| {1 - \sqrt {10} } \right| = - (1 - \sqrt {10} ) = \sqrt {10} - 1\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه نهم- آزمون آنلاین تمامی دروس پایه نهم
- گام به گام تمامی دروس پایه نهم
- ویدئو های آموزشی تمامی دروس پایه نهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه نهم
- فلش کارت های آماده دروس پایه نهم
- گنجینه ای جامع از انشاء های آماده پایه نهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه نهم



1736019749.png)















