جواب تمرین صفحه 76 درس 4 ریاضی دهم (معادله ها و نامعادله ها)

1

\(\begin{array}{l}{x^2} - 11x = - 10\\\\ \Rightarrow {x^2} - 11\,x + 10 = 0\\\\ \Rightarrow \left( {x - 10} \right)\left( {x - 1} \right) = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x - 10 = 0 \Rightarrow x = 10\\\end{array}\\{x - 1 = 0 \Rightarrow x = 1}\end{array}} \right.\end{array}\)

2

\(\begin{array}{l}5{t^2} = 20\\\\ \Rightarrow {t^2} = 4 \Rightarrow {t^2} - 4 = 0\\\\ \Rightarrow \left( {t - 2} \right)\left( {t + 2} \right) = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}t - 2 = 0 \Rightarrow t = 2\\\end{array}\\{t + 2 = 0 \Rightarrow t = - 2}\end{array}} \right.\end{array}\)

3

\(\begin{array}{l}5{a^2} - 7a = 2a(a - 3)\\\\ \Rightarrow 5{a^2} - 7a = 2{a^2} - 6a\\\\ \Rightarrow 3{a^2} - a = 0\\\\ \Rightarrow a\left( {3a - 1} \right) = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a = 0\\\end{array}\\{3a - 1 = 0 \Rightarrow a = \frac{1}{3}}\end{array}} \right.\end{array}\)

4

\(\begin{array}{l}4{k^2} - 12k + 8 = 0\\\\ \Rightarrow {k^2} - 3k + 2 = 0\\\\ \Rightarrow \left( {k - 2} \right)\left( {k - 1} \right) = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}k - 2 = 0 \Rightarrow k = 2\\\end{array}\\{k - 1 = 0 \Rightarrow k = 1}\end{array}} \right.\end{array}\)

1

\(\begin{array}{l}{n^2} - 2 = 26\\\\ \Rightarrow {n^2} = 28 \Rightarrow n = \pm \sqrt {28} = \pm 2\sqrt 7 \end{array}\)

2

\(\begin{array}{l}{x^2} + 12 = 3\\\\ \Rightarrow {x^2} = - 9 \Rightarrow x = \pm \sqrt { - 9} \otimes \end{array}\)

3

\(\begin{array}{l}{(3t - 2)^2} = 4\\\\\begin{array}{*{20}{l}}\begin{array}{l} \Rightarrow 3t - 2 = \pm \sqrt 4 = \pm 2\\\\ \Rightarrow 3t = 2 \pm 2 \Rightarrow t = \frac{{2 \pm 2}}{3}\\\end{array}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}t = \frac{{2 + 2}}{3} = \frac{4}{3}\\\end{array}\\{t = \frac{{2 - 2}}{3} = 0}\end{array}} \right.}\end{array}\end{array}\)

4

\(\begin{array}{l}3 - 3k = 3k(2k - 1)\\\\\begin{array}{*{20}{l}}\begin{array}{l} \Rightarrow 3 - 3k = 6{k^2} - 3k\\\\ \Rightarrow 3 = 6{k^2}\\\\ \Rightarrow \frac{3}{6} = {k^2} = \frac{1}{2}\\\end{array}\\{ \Rightarrow k = \pm \frac{{\sqrt 2 }}{2}}\end{array}\end{array}\)

1

\(\begin{array}{*{20}{l}}\begin{array}{l}{x^2} - 6x = 7\\\\ \Rightarrow {x^2} - 6x + {\left( {\frac{{ - 6}}{2}} \right)^2} = 7 + {\left( {\frac{{ - 6}}{2}} \right)^2}\\\\ \Rightarrow {\left( {x - 3} \right)^2} = 7 + 9 = 16\\\end{array}\\\begin{array}{l} \Rightarrow x - 3 = \pm 4\\\\ \Rightarrow x = 3 \pm 4 \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x = 7\\\end{array}\\{x = - 1}\end{array}} \right.\end{array}\end{array}\)

2

\(\begin{array}{*{20}{l}}\begin{array}{l}{s^2} - 3x + 3 = 0\\\\ \Rightarrow {s^2} - 3s = - 3\\\\ \Rightarrow {s^2} - 3s + {\left( {\frac{{ - 3}}{2}} \right)^2} = - 3 + {\left( {\frac{{ - 3}}{2}} \right)^2} = - 0/75\\\end{array}\\\begin{array}{l} \Rightarrow {\left( {s - 2/25} \right)^2} = - 0/75\\\\ \Rightarrow s - 2/25 = \pm \sqrt { - 0/75} \otimes \end{array}\end{array}\)

3

\(\begin{array}{l}{r^2} + 4r + 4 = 0\\\\ \Rightarrow {\left( {r + 2} \right)^2} = 0 \Rightarrow r + 2 = 0 \Rightarrow r = - 2\end{array}\)

4

\(\begin{array}{*{20}{l}}\begin{array}{l}2{a^2} + 5a - 3 = 0\\\\ \Rightarrow 2{a^2} + 5a = 3\\\\ \Rightarrow {a^2} + \frac{5}{2}a = \frac{3}{2}\\\\ \Rightarrow {a^2} + \frac{5}{2}a + {\left( {\frac{5}{4}} \right)^2} = \frac{3}{2} + {\left( {\frac{5}{4}} \right)^2}\end{array}\\\begin{array}{l}\\ \Rightarrow {\left( {a + \frac{5}{4}} \right)^2} = \frac{{49}}{{16}}\\\\ \Rightarrow a + \frac{5}{4} = \pm \frac{7}{4}\\\\ \Rightarrow a = - \frac{5}{4} \pm \frac{7}{4}\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a = - 3\\\end{array}\\{a = \frac{1}{2}}\end{array}} \right.\end{array}\end{array}\)

1

\(\begin{array}{*{20}{l}}\begin{array}{l}4{x^2} - 13x + 3 = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 4}\\{b = - 13}\\{c = 3}\end{array}} \right.\\\\ \Rightarrow \Delta = {b^2} - 4ac = {\left( { - 13} \right)^2} - 4\left( 4 \right)\left( 3 \right) = 121\\\end{array}\\\begin{array}{l} \Rightarrow x = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{13 \pm 11}}{{12}}\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{x_1} = \frac{{13 + 11}}{8} = 3\\\end{array}\\{{x_2} = \frac{{13 - 11}}{8} = \frac{1}{4}}\end{array}} \right.\end{array}\end{array}\)

2

\(\begin{array}{*{20}{l}}\begin{array}{l}r - {r^2} = 3\\\\ \Rightarrow - {r^2} + r - 3 = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 1}\\{b = 1}\\{c = - 3}\end{array}} \right.\\\\ \Rightarrow \Delta = {b^2} - 4ac = {\left( 1 \right)^2} - 4\left( { - 1} \right)\left( { - 3} \right) = 1 - 12\\\end{array}\\{ \Rightarrow \Delta = - 11 < 0}\end{array}\)

جواب ندارد

3

\(\begin{array}{l}{a^2} + 2\sqrt 3 a = 9\\\\\begin{array}{*{20}{l}}\begin{array}{l} \Rightarrow {a^2} + 2\sqrt 3 a - 9 = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 2\sqrt 3 }\\{c = - 9}\end{array}} \right.\\\end{array}\\\begin{array}{l} \Rightarrow \Delta = {b^2} - 4ac = {\left( {2\sqrt 3 } \right)^2} - 4\left( 1 \right)\left( { - 9} \right)\\\end{array}\\\begin{array}{l} \Rightarrow \Delta = 48\\\\ \Rightarrow x = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{ - 2\sqrt 3 \pm 4\sqrt 3 }}{2} = - \sqrt 3 \pm 2\sqrt 3 \\\end{array}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{x_1} = - \,3\sqrt 3 \\\end{array}\\{{x_2} = \sqrt 3 }\end{array}} \right.}\end{array}\end{array}\)

4

\(\begin{array}{*{20}{l}}\begin{array}{l}\frac{{{t^2}}}{3} - \frac{t}{2} - \frac{3}{2} = 0\\\\\mathop \Rightarrow \limits^{ \times 6} \,2{t^2} - 3t - 4 = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = - 3}\\{c = - 4}\end{array}} \right.\\\\ \Rightarrow \Delta = {b^2} - 4ac = {\left( { - 3} \right)^2} - 4\left( 2 \right)\left( { - 4} \right) = 41\\\end{array}\\\begin{array}{l} \Rightarrow x = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{3 \pm \sqrt {41} }}{4}\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{x_1} = \frac{{3 + \sqrt {41} }}{4}\\\end{array}\\{{x_2} = \frac{{3 - \sqrt {41} }}{4}}\end{array}} \right.\end{array}\end{array}\)

1

با روش ریشه گیری:

\({x^2} = 125 \Rightarrow x = \pm 5\sqrt 5 \)

2

با روش مربع کامل:

\({\left( {z - 3} \right)^2} = 0 \Rightarrow z - 3 = 0 \Rightarrow z = 3\)

3

با روش فرمول کلی:

\(\begin{array}{*{20}{l}}\begin{array}{l}4{a^2} + 3a - 1 = 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{A = 4}\\{B = 3}\\{C = - 1}\end{array}} \right.\\\\ \Rightarrow \Delta = {B^2} - 4AC = {\left( 3 \right)^2} - 4\left( 4 \right)\left( { - 1} \right) = 25\\\end{array}\\\begin{array}{l} \Rightarrow a = \frac{{ - B \pm \sqrt \Delta }}{{2A}} = \frac{{ - 3 \pm \sqrt {25} }}{8}\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{a_1} = \frac{{ - 3 + 5}}{8} = \frac{1}{4}\\\end{array}\\{{a_2} = \frac{{ - 3 - 5}}{8} = - 1}\end{array}} \right.\end{array}\end{array}\)

4

با روش فرمول کلی:

\(\begin{array}{*{20}{l}}\begin{array}{l} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{A = 1}\\{B = \sqrt 2 }\\{C = - 4}\end{array}} \right.\\\\ \Rightarrow \Delta = {B^2} - 4AC = {\left( {\sqrt 2 } \right)^2} - 4\left( 1 \right)\left( { - 4} \right) = 18\\\end{array}\\\begin{array}{l} \Rightarrow b = \frac{{ - B \pm \sqrt \Delta }}{{2A}} = \frac{{ - \sqrt 2 \pm 3\sqrt 2 }}{2}\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{b_1} = \frac{{ - \sqrt 2 + 3\sqrt 2 }}{2} = \sqrt 2 \\\end{array}\\{{b_2} = \frac{{ - \sqrt 2 - 3\sqrt 2 }}{2} = - 2\sqrt 2 }\end{array}} \right.\end{array}\end{array}\)

فرض کنیم که n یک عدد فرد باشد؛ بنابراین 2n+ یک عدد فرد است. در نتیجه داریم :

\(\begin{array}{*{20}{l}}\begin{array}{l}{n^2} + {\left( {n + 2} \right)^2} = 290\\\\ \Rightarrow {n^2} + {n^2} + 4n + 4 = 2{n^2} + 4n + 4 = 290\\\end{array}\\\begin{array}{l} \Rightarrow {n^2} + 2n + 2 = 145\\\\ \Rightarrow {n^2} + 2n = 143\\\\ \Rightarrow {n^2} + 2n + {\left( {\frac{2}{2}} \right)^2} = 143 + {\left( {\frac{2}{2}} \right)^2}\\\end{array}\\\begin{array}{l} \Rightarrow {\left( {n + 1} \right)^2} = 144\\\\ \Rightarrow n + 1 = \pm 12\\\\ \Rightarrow n = - 1 \pm 12\\\end{array}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}n = - 1 + 12 \Rightarrow n = 11 \Rightarrow \begin{array}{*{20}{c}}{}&{}\end{array}11\,,\,13\\\end{array}\\{n = - 1 - 12 \Rightarrow n = - 13 \Rightarrow \begin{array}{*{20}{c}}{}&{}\end{array} - 13\,,\, - 11}\end{array}} \right.}\end{array}\)

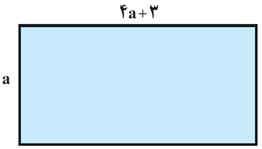
\(\begin{array}{*{20}{l}}\begin{array}{l}a\,,\,4a + 3\\\\ \Rightarrow a\left( {4a + 3} \right) = 45\\\\ \Rightarrow 4{a^2} + 3a - 45 = 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{A = 4}\\{B = 3}\\{C = - 45}\end{array}} \right.\\\end{array}\\\begin{array}{l} \Rightarrow \Delta = {B^2} - 4AC = {\left( 3 \right)^2} - 4\left( 4 \right)\left( { - 45} \right) = 729\\\end{array}\\\begin{array}{l} \Rightarrow a = \frac{{ - B \pm \sqrt \Delta }}{{2A}} = \frac{{ - 3 \pm \sqrt {729} }}{8} = \frac{{ - 3 \pm 27}}{8}\\\end{array}\\\begin{array}{l} \Rightarrow {a_1} = \frac{{ - 3 - 27}}{8} = - \frac{{15}}{4}\, \otimes \\\end{array}\\{ \Rightarrow {a_2} = \frac{{ - 3 + 27}}{8} = 3}\\\begin{array}{l}\\ \Rightarrow a = 3\end{array}\end{array}\)

بنابراین:

عرض = 3  و  طول = 15

\(\begin{array}{*{20}{l}}\begin{array}{l}n\;\;{\mkern 1mu} {\kern 1pt} ,\;\;{\mkern 1mu} {\kern 1pt} n + 4\,\,\,\\\\ \Rightarrow \left( {n + 4} \right)\left( {n + 4 + 4} \right) = 60\\\\ \Rightarrow \left( {n + 4} \right)\left( {n + 8} \right) = 60\\\end{array}\\\begin{array}{l} \Rightarrow {n^2} + 12n + 32 = 60\\\\ \Rightarrow {n^2} + 12n = 28\\\\ \Rightarrow {n^2} + 12n + {\left( {\frac{{12}}{2}} \right)^2} = 28 + {\left( {\frac{{12}}{2}} \right)^2}\\\end{array}\\\begin{array}{l} \Rightarrow {\left( {n + 6} \right)^2} = 64 \Rightarrow n + 6 = \pm \sqrt {64} \\\\ \Rightarrow n = - 6 \pm 8\\\end{array}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{n = 2}\\{n = - 14 \otimes }\end{array}} \right.\,\,\,\, \Rightarrow n = 2}\end{array}\)

2 سال و 6 سال سن دارند.

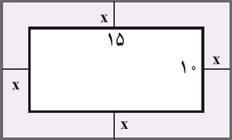
\(\begin{array}{*{20}{l}}\begin{array}{l}\left( {10 + 2x} \right)\left( {15 + 2x} \right) = 300\\\\ \Rightarrow 4{x^2} + 50x + 150 = 300\\\\ \Rightarrow 4{x^2} + 50x - 150 = 0\\\end{array}\\\begin{array}{l} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 4}\\{b = 50}\\{c = - 150}\end{array}} \right.\\\\ \Rightarrow \Delta = {b^2} - 4ac = {\left( {50} \right)^2} - 4\left( 4 \right)\left( { - 150} \right) = 4900\\\end{array}\\\begin{array}{l} \Rightarrow x = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{ - 50 \pm \sqrt {4900} }}{8} = \frac{{ - 50 \pm 70}}{8}\\\end{array}\\\begin{array}{l}{x_1} = \frac{{ - 50 - 70}}{8} = - 15\\\end{array}\\{{x_2} = \frac{{ - 50 + 70}}{8} = 2/5 \Rightarrow x = 2/5}\end{array}\)

بنابراین:

عرض = 15  و  طول = 20

اگر تعداد تیم ها را n  و هر تیم 1-n بازی دارد. پس با توجه به اینکه بین هر دو تیم تنها یک بازی صورت می گیرد و اصطلاحاً رفت و برگشتی نیست. در نتیجه کل بازی ها برابر \(\frac{{n\left( {n - 1} \right)}}{2}\)  است. بنابراین:

: الگو برای تعداد بازی ها \(\frac{{n\left( {n - 1} \right)}}{2}\) 

\(\begin{array}{*{20}{l}}\begin{array}{l}\frac{{n\left( {n - 1} \right)}}{2} = 45 \Rightarrow n\left( {n - 1} \right) = 90\\\\ \Rightarrow {n^2} - n - 90 = 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = - 1}\\{c = - 90}\end{array}} \right.\\\end{array}\\\begin{array}{l} \Rightarrow \Delta = {b^2} - 4ac = {\left( { - 1} \right)^2} - 4\left( 1 \right)\left( { - 90} \right) = 361\\\end{array}\\\begin{array}{l}n = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{1 \pm 19}}{2} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{n_1} = \frac{{1 - 19}}{2} = - 9 \otimes }\\{{n_2} = \frac{{1 + 19}}{2} = 10}\end{array}} \right.\,\,\,\,\\\\ \Rightarrow n = 10\;\;\;\;N = n - 1\end{array}\end{array}\)

10 تیم

\(\begin{array}{*{20}{l}}\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}P = 0/006{s^2} - 0/02s + 120\\\end{array}\\{{P_1} = 125}\end{array}} \right.\\\\ \Rightarrow 125 = 0/006{s^2} - 0/02s + 120\\\\ \Rightarrow 0/006{s^2} - 0/02s - 5 = 0\\\end{array}\\\begin{array}{l} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 0/006}\\{b = - 0/02}\\{c = - 5}\end{array}} \right.\\\\ \Rightarrow \Delta = {b^2} - 4ac = {\left( { - 0/02} \right)^2} - 4\left( {0/006} \right)\left( { - 5} \right) = 0/1204\\\end{array}\\\begin{array}{l} \Rightarrow s = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{0/02 \pm \sqrt {0/1204} }}{{0/012}}\\\\ \Rightarrow s = \frac{{0/02 + \sqrt {0/1204} }}{{0/012}} \simeq 31\end{array}\end{array}\)

31 سال