جواب تمرین صفحه 81 درس 4 ریاضی دهم (معادله ها و نامعادله ها)
تعداد بازدید : 84.75Mپاسخ تمرین صفحه 81 ریاضی دهم
-گام به گام تمرین صفحه 81 درس معادله ها و نامعادله ها
-تمرین صفحه 81 درس 4
-شما در حال مشاهده جواب تمرین صفحه 81 ریاضی دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 نمودار هر یک از سهمی های زیر را رسم کنید.
الف \(y = - {\left( {x + 1} \right)^2} - 3\)
ب \(y = 3{x^2} - 2\)
پ \(y = x - {x^2}\)
ت \(y = \frac{{{x^2}}}{2} + x - 4\)
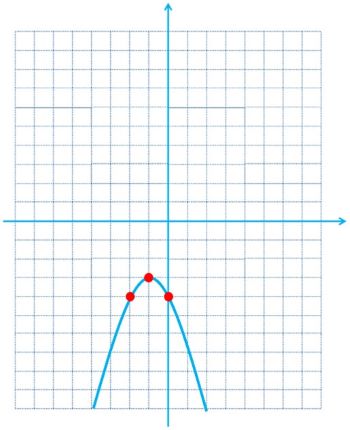
الف
\(\begin{array}{*{20}{l}}{y = - {{\left( {x + 1} \right)}^2} - 3}\\{x + 1 = 0 \Rightarrow {x_0} = - 1 \Rightarrow {y_0} = - {{\left( { - 1 + 1} \right)}^2} - 3 = 0 - 3 = - 3}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = - 1}\\{{y_0} = - 3}\end{array}} \right.}\\{ \Rightarrow {x_1} = - 2 \Rightarrow {y_1} = - {{\left( { - 2 + 1} \right)}^2} - 3 = - 1 - 3 = - 4}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = - 2}\\{{y_1} = - 4}\end{array}} \right.}\\{ \Rightarrow {x_2} = 0 \Rightarrow {y_2} = - {{\left( {0 + 1} \right)}^2} - 3 = - 1 - 3 = - 4}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_2} = 0}\\{{y_2} = - 4}\end{array}} \right.}\end{array}\)
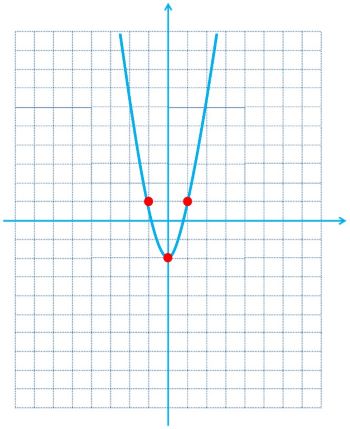
ب
\(\begin{array}{*{20}{l}}{y = 3{x^2} - 2}\\{{x_0} = 0 \Rightarrow {y_0} = 3{{\left( 0 \right)}^2} - 2 = 0 - 2 = - 2}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = 0}\\{{y_0} = - 2}\end{array}} \right.}\\{{x_1} = - 1 \Rightarrow {y_1} = 3{{\left( { - 1} \right)}^2} - 2 = 3 - 2 = 1}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = - 1}\\{{y_1} = 1}\end{array}} \right.}\\{{x_2} = 1 \Rightarrow {y_2} = 3{{\left( 1 \right)}^2} - 2 = 3 - 2 = 1}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_2} = 1}\\{{y_2} = 1}\end{array}} \right.}\end{array}\)
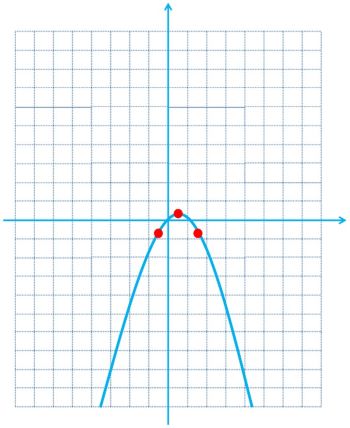
پ
\(\begin{array}{*{20}{l}}{y = x - {x^2} = - {{\left( {x - \frac{1}{2}} \right)}^2} + \frac{1}{4}}\\{x - \frac{1}{2} = 0 \Rightarrow {x_0} = \frac{1}{2} \Rightarrow {y_0} = - {{\left( {\frac{1}{2} - \frac{1}{2}} \right)}^2} + \frac{1}{4} = 0 + \frac{1}{4} = \frac{1}{4}}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = \frac{1}{2}}\\{{y_0} = \frac{1}{4}}\end{array}} \right.}\\{{x_1} = - \frac{1}{2} \Rightarrow {y_1} = - {{\left( { - \frac{1}{2} - \frac{1}{2}} \right)}^2} + \frac{1}{4} = - 1 + \frac{1}{4} = - \frac{3}{4}}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = - \frac{1}{2}}\\{{y_1} = - \frac{3}{4}}\end{array}} \right.}\\{{x_2} = \frac{3}{2} \Rightarrow {y_2} = - {{\left( {\frac{3}{2} - \frac{1}{2}} \right)}^2} + \frac{1}{4} = - 1 + \frac{1}{4} = - \frac{3}{4}}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_2} = \frac{3}{2}}\\{{y_2} = - \frac{3}{4}}\end{array}} \right.}\end{array}\)
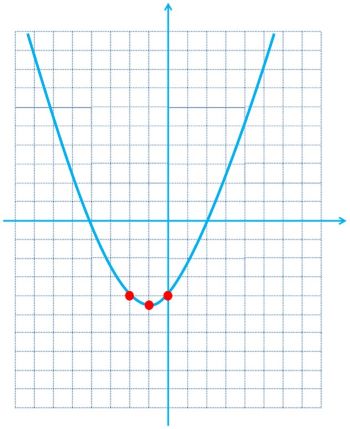
ت
\(\begin{array}{*{20}{l}}{y = \frac{{{x^2}}}{2} + x - 4 = \frac{1}{2}{{\left( {x + 1} \right)}^2} - \frac{9}{2}}\\{x + 1 = 0 \Rightarrow {x_0} = - 1 \Rightarrow {y_0} = \frac{1}{2}{{\left( { - 1 + 1} \right)}^2} - \frac{9}{2} = 0 - \frac{9}{2} = - \frac{9}{2}}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = - 1}\\{{y_0} = - \frac{9}{2}}\end{array}} \right.}\\{{x_1} = - 2 \Rightarrow {y_1} = \frac{1}{2}{{\left( { - 2 + 1} \right)}^2} - \frac{9}{2} = \frac{1}{2} - \frac{9}{2} = - 4}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = - 2}\\{{y_1} = - 4}\end{array}} \right.}\\{{x_2} = 0 \Rightarrow {y_2} = \frac{1}{2}{{\left( {0 + 1} \right)}^2} - \frac{9}{2} = \frac{1}{2} - \frac{9}{2} = - 4}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_2} = 0}\\{{y_2} = - 4}\end{array}} \right.}\end{array}\)
2 اگر (-2,5) و (0,5) دو نقطه از یک سهمی باشند، خط تقارن این سهمی را به دست آورید.
با توجه به اینکه عرض نقاط یکسان است، این دو نقطه نسبت به محور تقارن قرینه یکدیگرند؛ به عبارت دیگر محور تقارن از وسط طول های این دو نقطه می گذرد ؛ یعنی:
\({x_0} = \frac{{0 + ( - 2)}}{2} = - 1\)
در نتیجه خط 1-=x محور تقارن سهمی می باشد.
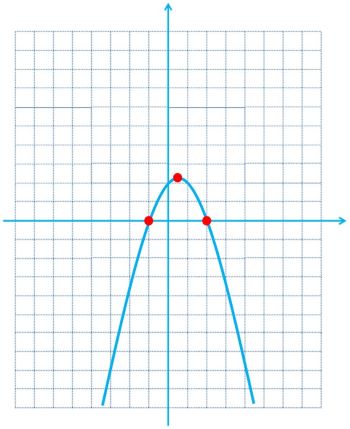
3 نمودار سهمی \(y = a{x^2} + bx + c\) ، محور yها را در نقطه ای به عرض 2 و محور xها را در نقاط به طول 1- و 2 قطع کرده است. معادلهٔ این سهمی را بنویسید و آن را رسم کنید.
\(\begin{array}{l}\begin{array}{*{20}{l}}\begin{array}{l}\left( {0{\kern 1pt} ,{\kern 1pt} 2} \right) \Rightarrow 2 = a{\left( 0 \right)^2} + b\left( 0 \right) + c \Rightarrow c = 2\\\end{array}\\\begin{array}{l}\left( { - 1{\kern 1pt} ,{\kern 1pt} 0} \right) \Rightarrow 0 = a{\left( { - 1} \right)^2} + b\left( { - 1} \right) + 2 \Rightarrow a - b = - 2\\\end{array}\\\begin{array}{l}\left( {2{\kern 1pt} ,{\kern 1pt} 0} \right) \Rightarrow 0 = a{\left( 2 \right)^2} + b\left( 2 \right) + 2 \Rightarrow 4a + 2b = - 2\\\end{array}\\{\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a - b = - 2\\\end{array}\\{4a + 2b = - 2}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a = - 1\\\end{array}\\{b = - 1}\end{array}} \right. \Rightarrow y = - {x^2} + x + 2}\end{array}\\\\\begin{array}{*{20}{l}}{y = - {x^2} + x + 2 = - {{\left( {x - \frac{1}{2}} \right)}^2} + \frac{9}{4}}\\\begin{array}{l}\\x - \frac{1}{2} = 0 \Rightarrow {x_0} = \frac{1}{2} \Rightarrow {y_0} = - {\left( {\frac{1}{2} - \frac{1}{2}} \right)^2} + \frac{9}{4} = \frac{9}{4}\end{array}\\\begin{array}{l}\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = \frac{1}{2}}\\{{y_0} = \frac{9}{4}}\end{array}} \right.\;\;{\mkern 1mu} {\kern 1pt} ,\;\;{\mkern 1mu} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}}{{x_1} = - 1}\\{{y_1} = 0}\end{array}} \right.\;\;{\mkern 1mu} {\kern 1pt} ,\;\;{\mkern 1mu} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}}{{x_2} = 2}\\{{y_2} = 0}\end{array}} \right.\end{array}\end{array}\end{array}\)
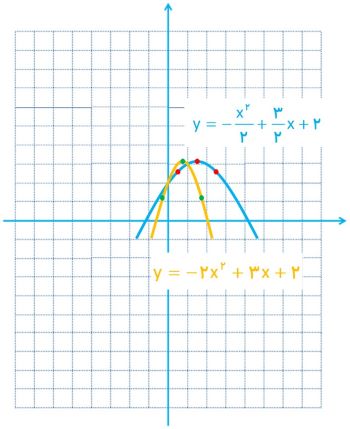
4 دو پرتابگر وزنه در یک مسابقهٔ ورزشی، وزنه های خود را با زاویه های متفاوت α و b که α<b است، پرتاب کرده اند. پرتابگر A، زاویه α را انتخاب می کند و مسیر طی شده از رابطۀ \(y = - \frac{{{x^2}}}{2} + \frac{3}{2}x + 2\) به دست می آید. پرتابگر B نیز زاویۀ b را انتخاب می کند و مسیر طی شده از رابطهٔ \(y = - 2{x^2} + 3x + 2\) به دست می آید. در هر دو معادله، y ارتفاع وزنه از سطح زمین و x مسافت افقی طی شده، بر حسب متر است.
الف مسیر حرکت هر کدام از وزنه ها را رسم کنید.
ب محل برخورد وزنه ها با زمین یا محور xها درچه نقاطی است؟ کدام یک از وزنه ها مسافت افقی بیشتری را طی کرده است؟
پ کدام یک از وزنه ها ارتفاع بیشتری از سطح زمین پیدا کرده است؟ اندازهٔ آنها را مشخص کنید.
الف
مسیر پرتابه A:
\(\begin{array}{*{20}{l}}{y = - \frac{{{x^2}}}{2} + \frac{3}{2}x + 2 = - \frac{1}{2}{{\left( {x - \frac{3}{2}} \right)}^2} + \frac{{25}}{8}}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = \frac{3}{2}}\\{{y_0} = \frac{{25}}{8}}\end{array}} \right.\;\;{\mkern 1mu} {\kern 1pt} ,\;\;{\mkern 1mu} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}}{{x_1} = \frac{1}{2}}\\{{y_1} = \frac{{21}}{8}}\end{array}} \right.\;\;{\mkern 1mu} {\kern 1pt} ,\;\;{\mkern 1mu} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}}{{x_2} = \frac{3}{2}}\\{{y_2} = \frac{{21}}{8}}\end{array}} \right.}\end{array}\)
مسیر پرتابه B:
\(\begin{array}{*{20}{l}}{y = - 2{x^2} + 3x + 2 = - 2{{\left( {x - \frac{3}{4}} \right)}^2} + \frac{{25}}{8}}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = \frac{3}{4}}\\{{y_0} = \frac{{25}}{8}}\end{array}} \right.\;\;{\mkern 1mu} {\kern 1pt} ,\;\;{\mkern 1mu} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}}{{x_1} = - \frac{1}{4}}\\{{y_1} = \frac{9}{8}}\end{array}} \right.\;\;{\mkern 1mu} {\kern 1pt} ,\;\;{\mkern 1mu} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}}{{x_2} = \frac{7}{4}}\\{{y_2} = \frac{9}{8}}\end{array}} \right.}\end{array}\)
ب
طول های برخورد پرتابه A با زمین:
\(\begin{array}{*{20}{l}}{ - \frac{{{x^2}}}{2} + \frac{3}{2}x + 2 = - \frac{1}{2}{{\left( {x - \frac{3}{2}} \right)}^2} + \frac{{25}}{8} = 0}\\{ \Rightarrow \frac{1}{2}{{\left( {x - \frac{3}{2}} \right)}^2} = \frac{{25}}{8} \Rightarrow {{\left( {x - \frac{3}{2}} \right)}^2} = \frac{{25}}{4}}\\{ \Rightarrow x - \frac{3}{2} = \pm \frac{5}{2} \Rightarrow x = \frac{3}{2} \pm \frac{5}{2} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = - 1}\\{{x_2} = 4}\end{array}} \right.}\\{}\\{ \Rightarrow \Delta {x_A} = {x_2} - {x_1} = 4 + 1 = 5}\end{array}\)
طول های برخورد پرتابه B با زمین:
\(\begin{array}{*{20}{l}}{ - 2{x^2} + 3x + 2 = - 2{{\left( {x - \frac{3}{4}} \right)}^2} + \frac{{25}}{8} = 0}\\{ \Rightarrow 2{{\left( {x - \frac{3}{4}} \right)}^2} = \frac{{25}}{8} \Rightarrow {{\left( {x - \frac{3}{4}} \right)}^2} = \frac{{25}}{{16}}}\\{ \Rightarrow x - \frac{3}{4} = \pm \frac{5}{4} \Rightarrow x = \frac{3}{4} \pm \frac{5}{4} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = - \frac{1}{4}}\\{{x_2} = 2}\end{array}} \right.}\\{ \Rightarrow \Delta {x_B} = {x_2} - {x_1} = 2 + \frac{1}{4} = \frac{9}{4}}\end{array}\)
پرتابه A مسیر افقی بیشتری رفته است:
\(\Delta {x_B} < \Delta {x_A}\)
پ
میزان ارتفاع همان عرض نقطه سهمی است که در این مورد هر دو عرض یکسان است، پس ارتفاع یکسانی پیموده اند؛ یعنی ارتفاع پیموده شده آنها \(\frac{{25}}{8}\) است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















