1736019749.png)
جواب تمرین صفحه 150 درس 7 ریاضی دهم (آمار و احتمال)
تعداد بازدید : 78.77Mپاسخ تمرین صفحه 150 ریاضی دهم
-گام به گام تمرین صفحه 150 درس آمار و احتمال
-تمرین صفحه 150 درس 7
-شما در حال مشاهده جواب تمرین صفحه 150 ریاضی دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
1 هر یک از اعداد طبیعی و زوجِ کوچک تر از 11 را روی یک کارت می نویسیم و یکی از این کارت ها را به تصادف برمی داریم:
الف فضای نمونه ای این آزمایش یا پدیدهٔ تصادفی را مشخص کنید.
ب چه تعداد پیشامد تصادفی را روی این فضای نمونه ای می توان تعریف کرد؟
پ پیشامد A را که در آن «عدد روی کارت انتخاب شده بر 4 بخش پذیر باشد» مشخص کنید.
الف S = {2 , 4 , 6 , 8 , 10}
ب n = 25 = 32
پ A = {4 , 8}
2 فرض کنید A و B و C سه پیشامد از فضای نمونه ای S باشند. هر یک از عبارت های توصیفی زیر را با نمودار ون نمایش دهید و هاشور بزنید.
الف پیشامدهای A و C رخ بدهند؛ ولی B رخ ندهد.
ب فقط پیشامد B رخ بدهد.
پ پیشامد B رخ بدهد و C رخ ندهد.
3 هر یک از ارقام 1 تا 8 را روی یک کارت می نویسیم و آنها را در یک کیسه قرار می دهیم؛ سپس یک کارت به تصادف از کیسه خارج می کنیم. هر یک از پیشامدهای زیر را تعیین کنید:
الف فضای نمونه ای و پیشامد A که در آن «عدد روی کارت زوج باشد»
ب پیشامد B که در آن «عدد روی کارت اول باشد»
پ پیشامد C که در آن «عدد رو شده بزرگ تر از 2 باشد».
الف S = {1 , 2 , 3 , 4 , 5 , 6 , 7 , 8}
A = {2 , 4 , 6 , 8}
ب B = {2 , 3 , 5 , 7}
پ C = {3 , 4 , 5 , 6 , 7 , 8}
4 خانواده ای دارای 3 فرزند است. فضای نمونه ای مربوط به فرزندان این خانواده را و پیشامد آنکه حداقل یکی از فرزندان دختر باشد را مشخص کنید.
p = پسر
d = دختر
S = {ppp , ppd , pdp , pdd , dpp , dpd , ddp , ddd}
A = {ppd , pdp , pdd , dpp , dpd , ddp , ddd}
5 سکه ای را به هوا می اندازیم. اگر پشت بیاید، یک تاس می اندازیم و اگر رو بیاید دو سکّهٔ دیگر را می اندازیم:
الف فضای نمونه ای این آزمایش تصادفی را مشخص کنید.
ب پیشامد آنکه «تاس زوج بیاید» را مشخص کنید.
پ پیشامد آنکه «حداقل 2 سکه رو بیاید» را مشخص کنید.
الف
p = پشت
r = رو
S = {(p,1) , (p,2) , (p,3) , (p,4) , (p,5) , (p,6) ,
(r,r,r) , (r,r,p) , (r,p,r) , (r,p,p)}
ب
A = {(p,2) , (p,4) , (p,6)}
پ
B = {(r,r,r) , (r,r,p) , (r,p,r)}
6 می خواهیم از بین 3 دانش آموز کلاس دهم رشتهٔ ریاضی و 2 دانش آموز دهم رشتهٔ تجربی یک تیم دو نفرهٔ تنیس روی میز انتخاب کنیم. اگر این عمل به تصادف صورت پذیرد، چقدر احتمال دارد:
الف هر دو نفر، از دانش آموزان کلاس دهم ریاضی باشند؟
ب هر دو نفر، هم رشته باشند؟
پ 1 نفر از رشتهٔ ریاضی و 1 نفر از رشتهٔ تجربی باشد؟
الف
\(P\left( A \right) = \frac{{\left( \begin{array}{l}3\\2\end{array} \right) \times \left( \begin{array}{l}2\\0\end{array} \right)}}{{\left( \begin{array}{l}5\\2\end{array} \right)}} = \frac{{3 \times 1}}{{10}} = \frac{3}{{10}}\)
ب
\(P\left( B \right) = \frac{{\left( {\begin{array}{*{20}{c}}3\\2\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}2\\0\end{array}} \right) + \left( {\begin{array}{*{20}{c}}3\\0\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}2\\2\end{array}} \right)}}{{\left( {\begin{array}{*{20}{c}}5\\2\end{array}} \right)}} = \frac{{3 \times 1 + 1 \times 1}}{{10}} = \frac{4}{{10}} = \frac{2}{5}\)
پ
\(P\left( C \right) = \frac{{\left( {\begin{array}{*{20}{c}}3\\1\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}2\\1\end{array}} \right)}}{{\left( {\begin{array}{*{20}{c}}5\\2\end{array}} \right)}} = \frac{{3 \times 2}}{{10}} = \frac{6}{{10}} = \frac{3}{5}\)
7 یک فروشگاه دو نوع کارت اعتباری A و B را می پذیرد. اگر 34 درصد از مشتریان کارت نوع A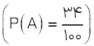 
و 62 درصد کارت نوع B و 15 درصد هر دو کارت را همراه داشته باشند، چقدر احتمال دارد مشتریان با در اختیار داشتن حداقل یکی از این دو کارت از این فروشگاه خرید کنند؟
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cap B} \right) = \frac{{34}}{{100}} + \frac{{62}}{{100}} - \frac{{15}}{{100}} = \frac{{81}}{{100}}\)
8 اگر 7 نفر که دو نفر آنها با هم برادرند، به تصادف در یک ردیف قرار بگیرند ، چقدر احتمال دارد:
الف دو برادر کنار یکدیگر نباشند؟
ب یکی از آنها در ابتدای ردیف و دیگری در انتهای ردیف قرار بگیرند؟
الف
A = دو برادر در کنار یکدیگر باشند
A’ = دو برادر در کنار یکدیگر نباشند
\(P\left( A \right) = \frac{{6!\: \times \:2!}}{{7!}} = \frac{2}{7}\;\;\: \Rightarrow \;\;\:P\left( {A'} \right) = 1 - P\left( A \right) = 1 - \frac{2}{7} = \frac{5}{7}\)
ب
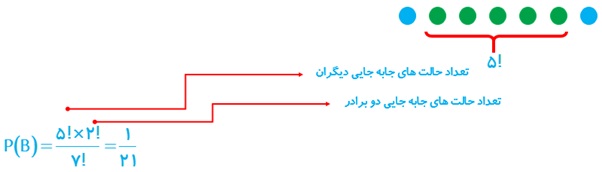
9 اگر A و B دو پیشامد از فضای نمونه ای S باشند و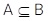
، ثابت کنید: \(P\left( A \right) \le P\left( B \right)\)
\(\begin{array}{l}A \subseteq B \Rightarrow n\left( A \right) \le n\left( B \right)\:\;\mathop \Rightarrow \limits^{ \div n\:\left( S \right)} \:\;\\\\\frac{{n\left( A \right)}}{{n\left( S \right)}} \le \frac{{n\left( B \right)}}{{n\left( S \right)}} \Rightarrow P\left( A \right) \le P\left( B \right)\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
