جواب تمرین صفحه 76 درس 4 ریاضی یازدهم تجربی (مثلثات)
تعداد بازدید : 84.82Mپاسخ تمرین صفحه 76 ریاضی یازدهم تجربی
-گام به گام تمرین صفحه 76 درس مثلثات
-تمرین صفحه 76 درس 4
-شما در حال مشاهده جواب تمرین صفحه 76 ریاضی یازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
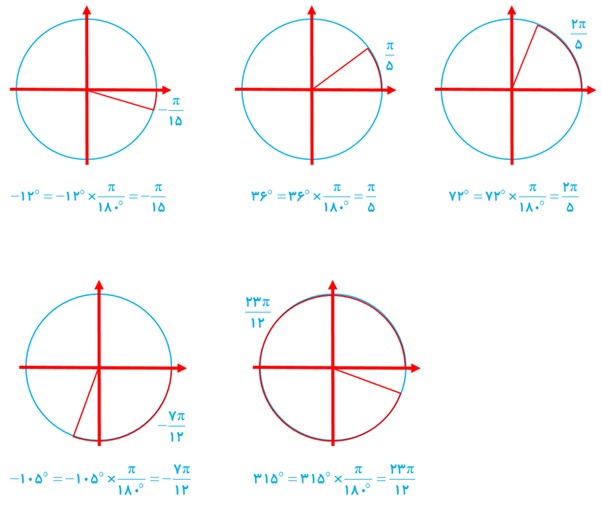
1 هریک از زاویه های °12- ، °36 ، °72 ، °105- و °315 را به رادیان تبدیل کنید و روی دایرهٔ مثلثاتی نشان دهید.
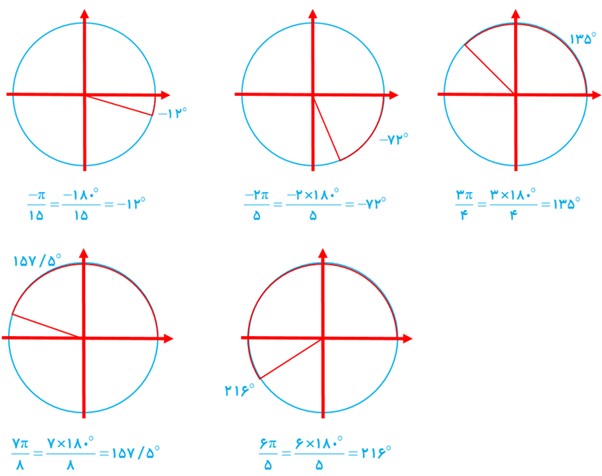
2 هریک از زاویه های \(\frac{{ - \pi }}{{18}}\) رادیان، \(\frac{{ - 2\pi }}{5}\) رادیان، \(\frac{{3\pi }}{4}\) رادیان، \(\frac{{7\pi }}{8}\) رادیان، \(\frac{{6\pi }}{5}\) رادیان، را به درجه تبدیل کنید و به طور تقریبی روی دایرهٔ مثلثاتی نشان دهید.
3 زاویۀ D برابر با \(\frac{\pi }{{20}}\) رادیان است. اندازهٔ این زاویه چند درجه است؟
\(D = \frac{\pi }{{20}} = \frac{{180^\circ }}{{20}} = 9^\circ \)
4 دایره ای به شعاع 10 سانتی متر مفروض است. اندازه زاویهٔ مرکزی مقابل به کمانی به طول 8 سانتی متر از این دایره چند رادیان است؟
\(\left\{ \begin{array}{l}r = 10\\l = 8\\\alpha = ?\end{array} \right. \Rightarrow \alpha = \frac{l}{r} = \frac{8}{{10}} = 0/{8^{rad}}\)
5 درستی یا نادرستی هر یک از جملات زیر را با ذکر دلیل بررسی کنید.
الف اگر زاویه بین دو ساق مثلث متساوی الساقینی 1 رادیان باشد، آنگاه اندازه قاعدهٔ این مثلث کوچک تر از اندازهٔ هر یک از ساق های آن است.
ب در دایره ای به شعاع 1 سانتی متر طول کمان روبه روی زاویه π رادیان تقریباً برابر با 3/14 سانتی متر است.
پ انتهای کمان زاویه \(\frac{{6\pi }}{5}\) رادیان در ربع دوم دایرۀ مثلثاتی قرار دارد.
ت زاویه های \(\frac{{2\pi }}{3}\) رادیان، \(\frac{\pi }{9}\) رادیان، \(\frac{{7\pi }}{{36}}\) رادیان، زوایای یک مثلث را تشکیل می دهند.
الف
می دانیم که 1 رادیان تقریبا برابر 57/3 درجه است.بنابراین با توجه به اینکه مثلث متساوی الساقین است، بنابراین اندازه دو زاویه مجاور ساق را می توان بدست آورد که برابر 61/35 درجه می باشد. همچنین می دانیم که در هر ضلع مثلث، ضلع مقابل به زاویه بزرگتر، بزرگتر از ضلع مقابل به زاویه کوچکتر است.پس طول قاعده کوچکتر از طول ساق ها خواهد بود. در نتیجه عبارت فوق درست می باشد.
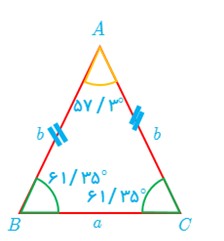
\(\hat A < \hat B = \hat C \Rightarrow a < b\)
ب
درست می باشد؛ زیرا:
\(\left\{ \begin{array}{l}r = {1^{cm}}\\l \simeq 3/{14^{cm}}\\\alpha = {\pi ^{rad}}\end{array} \right. \Rightarrow \alpha = \frac{l}{r} \Rightarrow l = r \cdot \alpha = {1^{cm}} \times {\pi ^{rad}} = {\pi ^{cm}} \simeq 3/{14^{cm}}\)
پ
درست نمی باشد؛ زیرا:
\(\left. \begin{array}{l}\frac{{6\pi }}{5} = \frac{{6 \times {{180}^ \circ }}}{5} = {216^ \circ }\\{90^ \circ } < \begin{array}{*{20}{c}}{}&{}&{}\end{array} < {180^ \circ }\end{array} \right\} \Rightarrow {180^ \circ } < {216^ \circ }\)
ربع سوم
ت
مجموع زاویای یک مثلث برابر با 180 درجه یا π رادیان خواهد بود. بنابراین داریم:
\(\frac{{2\pi }}{3} + \frac{\pi }{9} + \frac{{7\pi }}{{36}} = \frac{{24\pi }}{{36}} + \frac{{4\pi }}{{36}} + \frac{{7\pi }}{{36}} = \frac{{35\pi }}{{36}}\)
در نتیجه، زوایای داده شده، زوایای داخلی یک مثلث نیستند. پس عبارت نوشته شده، نادرست می باشد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















