گام به گام مرور فصل 7 صفحه 96 درس 7 ریاضی هفتم (توان و جذر)

1 توان:

توان به معنی ضرب مکرر یک عدد است. به عنوان مثال:

\(\begin{array}{l}{2^3} = 2 \times 2 \times 2 = 8\\\\{3^4} = 3 \times 3 \times 3 \times 3 = 81\\\\{5^3} = 5 \times 5 \times 5 = 125\end{array}\)

2 پایه:

عددی که باید ضرب شود. در عبارت \({3^4}\) ، عدد 3 پایه و عدد 4 توان می باشد. همچنین در عبارت \({5^2}\) ، عدد 5 پایه و عدد 2 توان می باشد.

3 مجذور:

توان دوم یک عدد به عنوان «مجذور» شناخته می‌شود؛ مثلاً:

\( = {6^2} = 6 \times 6 = 36\) مجذور عدد 6

4 مکعب:

توان سوم یک عدد به عنوان «مکعب» شناخته می‌شود؛ مثلاً:

 مکعب عدد 7\( = {7^2} = 7 \times 7 \times 7 = 343\)

5 جذر:

جذر یک عدد، عددی است که با ضرب شدن در خودش، آن عدد را بدهد و آن را با نماد \(\sqrt {} \) نشان می دهند؛ برای مثال، جذر ۹ برابر 3 است؛ زیرا:

\(\sqrt 9 = 3 \Rightarrow 3 \times 3 = 9\)

یا مثلاً جذر 64 برابر 8 است؛ زیرا:

\(\sqrt {64} = 8 \Rightarrow 8 \times 8 = 64\)

6 جذر تقریبی:

جذر تقریبی یک عدد عددی است که نزدیک به جذر دقیق آن عدد باشد. به عنوان مثال:

\(\begin{array}{l}\sqrt {10} \simeq 3/16\\\\\sqrt 8 \simeq 2/82\\\\\sqrt {27} \simeq 5/20\end{array}\)

1 محاسبهٔ عدد توان دار:

برای محاسبه عددی که توان دارد، عدد پایه را به تعداد توان در خودش ضرب می‌کنیم؛ به عنوان مثال:

\(\begin{array}{l}{4^3} = 4 \times 4 \times 4 = 64\\\\{5^4} = 5 \times 5 \times 5 \times 5 = 625\\\\{3^6} = 3 \times 3 \times 3 \times 3 \times 3 \times 3 = 729\end{array}\)

2 محاسبهٔ یک عبارت توان دار با رعایت ترتیب:

در محاسبه عبارات ریاضی باید ترتیب عملیات ریاضی را رعایت کنیم (پرانتز، توان، ضرب و تقسیم، جمع و تفریق)؛ به عنوان مثال:

\(3 + {2^3} \times 2 = 3 + 8 \times 2 = 3 + 16 = 19\)

یا اینکه:

\(\begin{array}{l}4 - {5^2}({2^3} - 9) = 4 - 25(8 - 9) = \\\\4 - 25( - 1) = 4 + 25 = 29\end{array}\)

3 تأثیر پرانتز در محاسبهٔ عبارت توان دار:

پرانتز‌ها ترتیب عملیات را تغییر می‌دهند؛ به عنوان مثال:

\({(2 + 3)^3} = {5^3} = 5 \times 5 \times 5 = 625\)

حال اگر پرانتز نداشته باشیم، مقدار عبارت به این صورت می شود:

\(\begin{array}{l}2 + {3^3} = 2 + {3^3} = 2 + 3 \times 3 \times 3 = \\\\2 + 27 = 29\end{array}\)

و اینکه:

\(\begin{array}{l}{(2 + 3)^3} = 625\\\\{2^3} + {3^3} = 8 + 27 = 35\\\\ \Rightarrow {(2 + 3)^3} \ne {2^3} + {3^3}\end{array}\)

همانطور که می بینیم دو مقدار دو عبارت \({(2 + 3)^3}\) و \({2^3} + {3^3}\) با یکدیگر برابر نیستند.

4 محاسبهٔ عبارت توان دار با پایه های منفی:

اگر پایه منفی باشد، توان زوج، مثبت و توان فرد، منفی می‌شود؛ به عنوان مثال:

\(\begin{array}{l}{( - 2)^1} = - 2\\\\{( - 2)^2} = ( - 2) \times ( - 2) = 4\\\\{( - 2)^3} = ( - 2) \times ( - 2) \times ( - 2) = - 8\\\\{( - 2)^4} = ( - 2) \times ( - 2) \times ( - 2) \times ( - 2) = 16\end{array}\)

5 توان صفر:

هر عددی (به غیر از صفر) به توان صفر برابر با ۱ است؛ به عبارتی دیگر:

\({a^0} = 1\,\,\,\,\,(a \ne 0)\)

به عنوان مثال:

\(\begin{array}{l}{7^0} = 1\\\\2/{5^0} = 1\\\\{\left( { - \frac{{25}}{{36}}} \right)^0} = 1\\\\{1^0} = 1\end{array}\)

6 قانون ضرب با پایه های مساوی:

قانون ضرب با پایه‌های مساوی یعنی زمانی که دو عدد با پایه‌های یکسان ولی توان‌های متفاوت را ضرب می‌کنیم. برای محاسبه این نوع ضرب ها، یکی از پایه ها را نوشته و توان‌ها را با هم جمع می‌کنیم؛ به عبارتی دیگر:

\({a^n} \times {a^m} = {a^{n + m}}\)

به عنوان مثال:

\(\begin{array}{l}{2^5} \times {2^4} = {2^{5 + 4}} = {2^9}\\\\{( - 3)^7} \times {( - 3)^2} = {( - 3)^{7 + 2}} = {( - 3)^9}\\\\1/{1^4} \times 1/{1^2} = 1/{1^{4 + 2}} = 1/{1^6}\end{array}\)

7 استفاده از قانون ضرب با پایه های مساوی در محاسبه:

قانون ضرب با پایه‌های مساوی به ما کمک می‌کند تا محاسباتی که شامل توان‌ها هستند را به راحتی و سریع‌تر انجام دهیم. این قانون بیان می‌کند که اگر دو عدد با پایه‌های یکسان و توان‌های متفاوت را ضرب کنیم، می‌توانیم توان‌ها را با هم جمع کرده و نتیجه را به دست آوریم. این روش در محاسبات علمی و مهندسی بسیار کاربردی است. به عنوان مثال می خواهیم حاصل عبارت زیر را بدست آوریم:

\(2/{5^2} \times {3^3} \times {4^6} \times {3^5} \times 16 \times {\left( {\frac{5}{2}} \right)^6} = \)

ابتدا پایه های مساوی را مشخص می کنیم و کنار یکدیگر می نویسیم:

\(\begin{array}{l}2/{5^2} \times {3^3} \times {4^6} \times {3^5} \times 16 \times 2/{5^6} = \\\\2/{5^2} \times 2/{5^6} \times {3^3} \times {3^5} \times {4^6} \times 16 = \end{array}\)

می توانیم به جای عدد 16، معادل آن یعنی \({4^2}\) را جایگزین آن کنیم:

\(\begin{array}{l}2/{5^2} \times {3^3} \times {4^6} \times {3^5} \times 16 \times 2/{5^6} = \\\\2/{5^2} \times 2/{5^6} \times {3^3} \times {3^5} \times {4^6} \times {4^2} = \end{array}\)

حال با استفاده از قانون «ضرب با پایه های مساوی» می توانیم بنویسیم:

\(\begin{array}{l}2/{5^2} \times {3^3} \times {4^6} \times {3^5} \times 16 \times 2/{5^6} = \\\\2/{5^{2 + 6}} \times {3^{3 + 5}} \times {4^{6 + 2}} = \\\\2/{5^8} \times {3^8} \times {4^8} = \end{array}\)

حال با استفاده از قانون «ضرب با توان های مساوی» که در شماره بعدی آن را توضیح می دهیم، پایه ها را در هم ضرب کرده و یکی از توان ها را می نویسیم:

\(\begin{array}{l}2/{5^8} \times {3^8} \times {4^8} = {(2/5 \times 3 \times 4)^8} = \\\\{30^8}\end{array}\)

بنابراین حاصل عبارت اصلی به این صورت می شود:

\(\begin{array}{l}2/{5^2} \times {3^3} \times {4^6} \times {3^5} \times 16 \times {\left( {\frac{5}{2}} \right)^6} = \\\\{30^8}\end{array}\)

8 قانون ضرب با توان های مساوی:

قانون ضرب با توان‌های مساوی یعنی زمانی که دو عدد با توان‌های یکسان ولی پایه‌های متفاوت را ضرب می‌کنیم، پایه‌ها را با هم ضرب می‌کنیم و توان ثابت می‌ماند؛ به عبارتی دیگر:

\({a^n} \times {b^n} = {(a \times b)^n}\)

به عنوان مثال:

\(\begin{array}{l}{2^5} \times {3^5} = {(2 \times 3)^5} = {6^5}\\\\{( - 3)^2} \times {5^2} = {( - 3 \times 5)^2} = {( - 15)^2}\\\\1/{1^4} \times {10^4} = {(1/1 \times 10)^4} = {11^4}\end{array}\)

9 استفاده از قانون ضرب با پایه های مساوی در تجزیهٔ عددها:

قانون ضرب با پایه‌های مساوی به ما کمک می‌کند تا اعداد بزرگ را به عوامل کوچکتر با پایه‌های یکسان تجزیه کنیم. این قانون بسیار کاربردی است زیرا می‌تواند محاسبات ریاضی را آسان‌تر کند و ما را از انجام محاسبات طولانی و پیچیده نجات دهد. تجزیه های اعداد را با کمک «درخت تجزیه» بدست می آوریم و سپس ضرب ها را به صورت ضرب اعداد توان دار می نویسیم؛ به عنوان مثال می خواهیم عدد 10,500 را با عامل های اول تجزیه کنیم و به صورت ضرب اعداد توان دار بنویسیم. برای این کار ابتدا درخت تجزیه آن را تشکیل می دهیم و به عامل های اول تجزیه می کنیم:

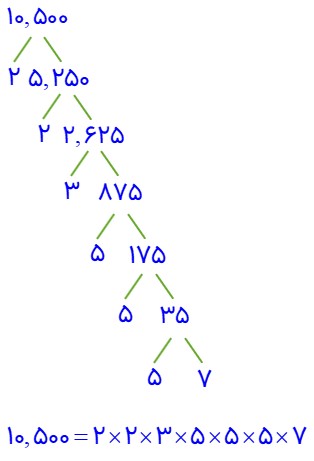
حال کافی است که تساوی به دست آمده را به صورت اعداد توان دار بنویسیم:

\(10,500 = {2^2} \times 3 \times {5^3} \times 7\)

10 ساده کردن یک عبارت توان دار:

ساده کردن عبارات توان‌دار یکی از روش‌های مهم در ریاضیات است که به ما کمک می‌کند تا معادلات پیچیده را به صورتی ساده‌تر و قابل فهم‌تر تبدیل کنیم. این فرآیند به ما امکان می‌دهد تا به سرعت و دقت بیشتری به نتایج نهایی برسیم. اصول ساده کردن عبارات توان‌دار را که در این فصل آن ها را یاد گرفتیم، در زیر آمده است:

الف قانون ضرب با پایه‌های مساوی:

\({a^n} \times {a^m} = {a^{n + m}}\)

ب قانون ضرب با توان‌های مساوی:

\({a^n} \times {b^n} = {(a \times b)^n}\)

برای مثال می خواهیم با استفاده از این دو قانون، عبارت ریاضی زیر را ساده کنیم:

\({9^3} \times {12^5} \times {8^2} \times {2^3} \times {6^5} = \)

ابتدا سعی می کنیم که بر اساس قانون «ضرب با توان های مساوی»، این عبارت را ساده کنیم:

\(\begin{array}{l}{9^3} \times {8^2} \times {2^3} \times {12^5} \times {6^5} = \\\\{9^3} \times {8^2} \times {2^3} \times {(12 \times 6)^5} = \\\\{9^3} \times {8^2} \times {2^3} \times {72^5} = \end{array}\)

همچنین می دانیم که عبارت \({2^3}\) برابر با 8 می باشد؛ بنابراین این عبارت را با جایگزینی این تساوی ساده تر می کنیم:

\(\begin{array}{l}{9^3} \times {8^2} \times 8 \times {72^5} = \\\\{9^3} \times {8^2} \times {8^1} \times {72^5} = \\\\{9^3} \times {8^{2 + 1}} \times {72^5} = \\\\{9^3} \times {8^3} \times {72^5} = \\\\{(9 \times 8)^3} \times {72^5} = \\\\{72^3} \times {72^5} = \end{array}\)

حال به کمک قانون «ضرب با پایه‌های مساوی» عبارت بدست آمده را ساده می کنیم:

\({72^{3 + 5}} = {72^8}\)

پس عبارت بالا به صورت زیر می شود:

\({9^3} \times {12^5} \times {8^2} \times {2^3} \times {6^5} = {72^8}\)

11 مفهوم مجذور و مکعب:

الف مجذور:

مجذور به معنای ضرب یک عدد در خودش است. به عبارت دیگر، وقتی یک عدد را به توان دو می‌رسانیم، مجذور آن عدد را به دست می‌آوریم؛ به عنوان مثال، اگر عدد 5 را در نظر بگیریم، مجذور آن به صورت زیر محاسبه می‌شود:

 مجذور عدد 5\( = {5^2} = 5 \times 5 = 25\)

کاربرد مجذور (محاسبه مساحت مربع):

اگر طول ضلع یک مربع را بدانیم، با مجذور آن طول، مساحت مربع را محاسبه می‌کنیم. مثلا می خواهیم مساحت مربعی به طول ضلع 4 را بدست آوریم. مساحت آن مربع برابر است با مجذور 4 یعنی 16

 مساحت مربع\( = {4^2} = 4 \times 4 = 16\)

ب مکعب:

مکعب به معنای ضرب یک عدد در خودش دو بار است. به عبارت دیگر، وقتی یک عدد را به توان سه می‌رسانیم، مکعب آن عدد را به دست می‌آوریم؛ به عنوان مثال، اگر عدد 4 را در نظر بگیریم، مکعب آن به صورت زیر محاسبه می‌شود:

 مکعب عدد 4\( = {4^3} = 4 \times 4 \times 4 = 64\)

کاربرد مکعب (محاسبه حجم مکعب):

اگر طول یال یک مکعب را بدانیم، با مکعب آن طول، حجم مکعب را محاسبه می‌کنیم. مثلا می خواهیم حجم مکعبی به طول یال 5 را بدست آوریم. حجم آن مکعب برابر است با مکعب 5 یعنی 125

\( = {5^3} = 5 \times 5 \times 5 = 125\) حجم مکعب

12 مفهوم جذر و ریشه:

الف جذر:

جذر یک عدد، عددی است که با ضرب شدن در خودش، آن عدد را بدهد و آن را با نماد \(\sqrt {} \) نشان می دهند؛ برای مثال، جذر ۹ برابر 3 است؛ زیرا:

\(\sqrt 9 = 3 \Rightarrow 3 \times 3 = 9\)

یا مثلاً جذر 64 برابر 8 است؛ زیرا:

\(\sqrt {64} = 8 \Rightarrow 8 \times 8 = 64\)

ب ریشه:

ریشه به معنای یافتن عددهایی است که وقتی در هم ضرب شوند، مقدار اصلی را بدهند. ریشه می‌تواند به دو صورت باشد:

1 ریشه دوم:

ریشه دوم (یا به اختصار در این کتاب درسی «ریشه!») همان جذر است که در بالا توضیح داده شد.

توجه:

مقدار ریشه دوم همواره عددی مثبت می باشد!

13 پیدا کردن جذر یا ریشهٔ عددهای مربع کامل و جذر تقریبی:

الف جذر عددهای مربع کامل:

عددهای مربع کامل عددهایی هستند که جذرشان یک عدد صحیح است. برای مثال، ۱، ۴، ۹، ۱۶، و ۲۵ مربع کامل هستند.

 جذر عدد 1\( = \sqrt {\,1\,} = 1 \Rightarrow 1 \times 1 = 1\)

 جذر عدد 4\( = \sqrt {\,4\,} = 2 \Rightarrow 2 \times 2 = 4\)

 جذر عدد 9\( = \sqrt {\,9\,} = 3 \Rightarrow 3 \times 3 = 9\)

 جذر عدد 16\( = \sqrt {16} = 4 \Rightarrow 4 \times 4 = 16\)

 جذر عدد 25\( = \sqrt {25} = 5 \Rightarrow 5 \times 5 = 25\)

ب جذر تقریبی:

در مواردی که عدد مربع کامل نیست، باید جذر تقریبی آن را پیدا کنیم. برای این کار ابتدا بررسی می کنیم ببینیم که عددی که می خواهیم جذر تقریبی آن را بدست آوریم، بین کدام دو عدد دارای مربع کامل است.

\(\begin{array}{l}\sqrt x = ?\\\\{m^2} < x < {n^2}\\\\m < \sqrt x < n\end{array}\)

بعد از آن، جذر اعداد مربع کامل را می گیریم. میانگین دو عدد بدست آمده را محاسبه می کنیم و مربع آن را بدست می آوریم.

\(\frac{{m + n}}{2} \to {(\frac{{m + n}}{2})^2}\)

حال بررسی می کنیم که آیا عددی که می خواهیم از آن جذر بگیریم، از این عدد کوچکتر بود، جذر عدد مورد نظر ما بین عدد با مربع کوچکتر  و میانگین دو عدد قرار دارد.

\(\begin{array}{l}{m^2} < x < {(\frac{{m + n}}{2})^2}\\\\m < \sqrt x < \frac{{m + n}}{2}\end{array}\)

حال این اعداد با رقم اول اعشار بین این دو عدد را در یک جدول نوشته و توان دوم آن ها را بدست می آوریم. آن عددی که کوچکتر و نزدیکتر به عددی که جذر آن را می خواهیم بگیریم، باشد، جواب مسئله می باشد.

اگر جذر عدد مورد نظر ما بین میانگین دو عدد و عدد با مربع کوچکتر قرار داشته باشد، یعنی:

\(\begin{array}{l}{(\frac{{m + n}}{2})^2} < x < {n^2}\\\\\frac{{m + n}}{2} < \sqrt x < n\end{array}\)

در این صورت مثل کاری که در بالا توضیح دادیم، این بار بین دو عدد مورد نظر انجام می دیم. آن عددی که کوچکتر و نزدیکتر به عددی که جذر آن را می خواهیم بگیریم، باشد، جواب مسئله می باشد.

با دو مثال، این روش را توضیح می دهیم؛ ابتدا جذر عددی را به دست می آوریم که از میانگین جذر دو عدد مربع کامل کمتر باشد:

\(\begin{array}{l}\sqrt {41} = ?\\\\36 < 41 < 49\\\\6 < \sqrt {41} < 7\\\\\frac{{6 + 7}}{2} = 6/5\\\\{(6/5)^2} = 42/25 \Rightarrow 41 < 42/25\\\\6 < \sqrt {41} < 6/5\end{array}\)

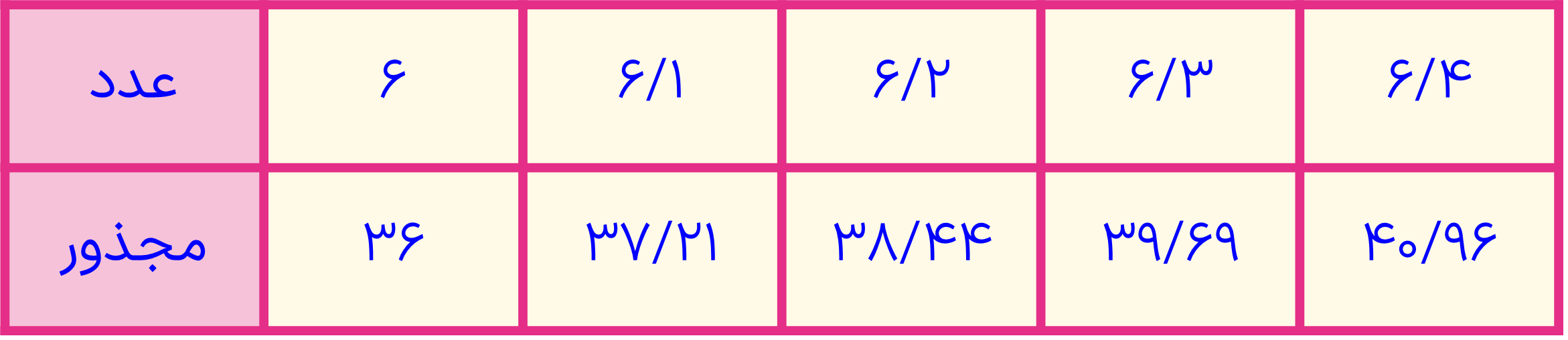
همانطور که می بینیم عدد 6/4 نزدیکترین عدد به جذر عدد 41 می باشد؛ زیرا که توان دوم آن به عدد 41 نزدیکتر است نسبت به باقی اعداد ردیف مجذور:

\(\sqrt {41} = 6/4\)

حال جذر عددی را به دست می آوریم که از میانگین جذر دو عدد مربع کامل بیشتر باشد:

\(\begin{array}{l}\sqrt {47} = ?\\\\36 < 47 < 49\\\\6 < \sqrt {47} < 7\\\\\frac{{6 + 7}}{2} = 6/5\\\\{(6/5)^2} = 42/25 \Rightarrow 47 > 42/25\\\\6/5 < \sqrt {47} < 7\end{array}\)

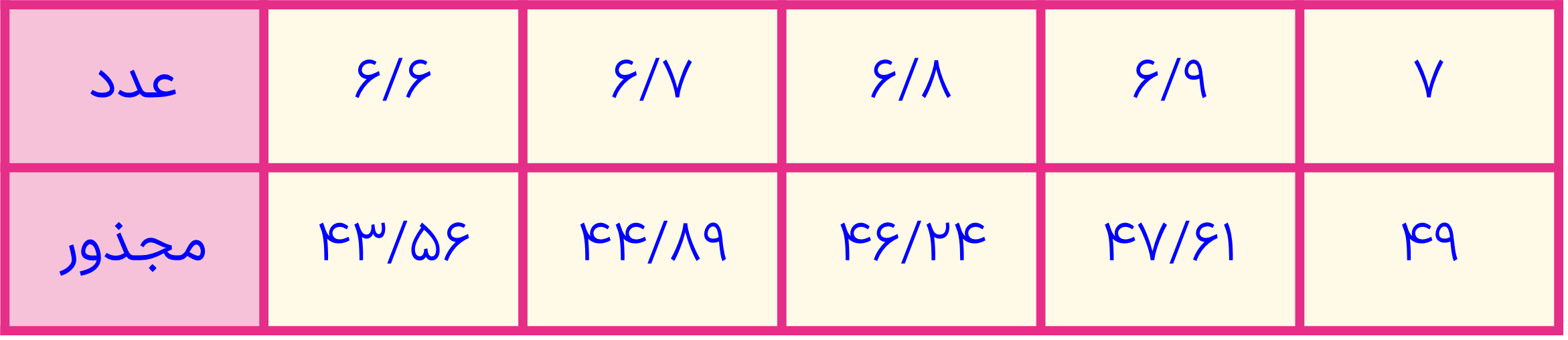
این روش برای اینکه جذر اعداد را تا یک رقم اعشار بدست آوریم. اگر بخواهیم تا دو رقم اعشار آن را بدست آوریم، کافی است که میانگین عدد بدست آمده و عدد اعشاری بعدی بزرگتر از این عدد را بدست آوریم و به روشی که در بالا توضیح دادیم، جذر عدد مورد نظر را تا دو رقم اعشار بدست آوریم. برای بدست آوردن رقم های بعدی اعشار نیز همین کار را می توانیم ادامه دهیم.

\(\begin{array}{l}{\left( {{2^3} + {0^2}} \right)^1} + {2^2} \times {3^2} - {1^3} = \\\\{\left( {8 + 0} \right)^1} + 4 \times 9 - 1 = \\\\8 + 36 - 1 = 43\end{array}\)

\(\begin{array}{l}{\left( {0/25} \right)^2} \times {\left( {\frac{1}{4}} \right)^3} \times \frac{1}{{{4^5}}} = \\\\{\left( {\frac{1}{4}} \right)^2} \times {\left( {\frac{1}{4}} \right)^3} \times \frac{{{1^5}}}{{{4^5}}} = \\\\{\left( {\frac{1}{4}} \right)^2} \times {\left( {\frac{1}{4}} \right)^3} \times {\left( {\frac{1}{4}} \right)^5} = \\\\{\left( {\frac{1}{4}} \right)^{2 + 3 + 5}} = {\left( {\frac{1}{4}} \right)^{10}}\end{array}\)

\(\begin{array}{l}{4^2} \times {8^3} \times {6^2} \times {3^3} = \\\\{4^2} \times {6^2} \times {8^3} \times {3^3} = \\\\{(4 \times 6)^2} \times {(8 \times 3)^3} = \\\\{24^2} \times {24^3} = {24^{2 + 3}} = {24^5}\end{array}\)

\(\begin{array}{l}\sqrt {32} \\\\25 < 32 < 36\\\\\sqrt {25} < \sqrt {32} < \sqrt {36} \\\\5 < \sqrt {32} < 6\end{array}\)

\(\sqrt {32} \) به عدد 6 نزدیک تر است؛ زیرا عدد 32 به عدد 36 نزدیک تر است:

در ردیف مجذور، چون عدد 32/49 نسبت به عدد 31/36 نزدیکتر به عدد 32 است، بنابراین داریم:

\(\sqrt {32} \simeq 5/7\)

-11 و 11 ریشه های دوم عدد 121 هستند؛ زیرا:

\(\begin{array}{l}{( - 11)^2} = ( - 11) \times ( - 11) = 121\\\\{11^2} = 11 \times 11 = 121\end{array}\)

حال تساوی های زیر را کامل می کنیم:

\(\begin{array}{l}\sqrt {49} = 7\\\\ - \sqrt {121} = - 11\\\\ - \sqrt {25} = - 5\\\\\sqrt {121} = 11\end{array}\)