جواب تمرین صفحه 86 درس 7 ریاضی هفتم (توان و جذر)
تعداد بازدید : 80.83Mپاسخ تمرین صفحه 86 ریاضی هفتم
-گام به گام تمرین صفحه 86 درس توان و جذر
-تمرین صفحه 86 درس 7
-شما در حال مشاهده جواب تمرین صفحه 86 ریاضی هفتم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 با توجه به شکل های زیر، مساحت و حجم های خواسته شده را با عبارت های توان دار جبری نمایش دهید.
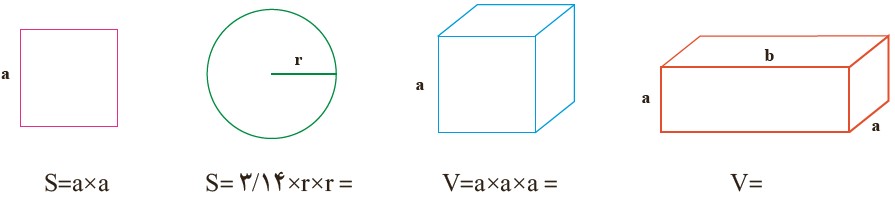
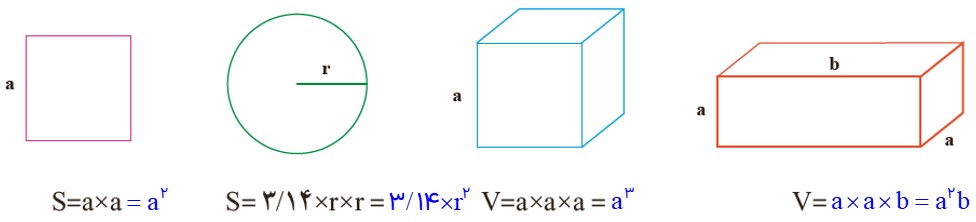
2 جمله های کلامی زیر را به صورت عبارت جبری نشان دهید.
هر عدد به توان یک، برابر خودش می شود:
\({a^1} = a\)
یک به توان هر عدد، برابر یک می شود:
مجذور هر عدد، یعنی آن عدد به توان 2 :
= مجذور a
مکعب یک عدد، یعنی آن عدد به توان 3 :
= مکعب x
صفر به توان هر عدد جز صفر، برابراست با:
یک به توان هر عدد، برابر یک می شود:
\({1^n} = 1\)
مجذور هر عدد، یعنی آن عدد به توان 2 :
\({a^2}\) = مجذور a
مکعب یک عدد، یعنی آن عدد به توان 3 :
\({x^3}\) = مکعب x
صفر به توان هر عدد جز صفر، برابر است با: صفر
\({0^n} = 0\,\,\,\,\,(n \ne 0)\)

اما در اصل:
صفر به توان هر عدد مثبت، برابر است با صفر
\({0^n} = 0\,\,\,\,\,(n > 0)\)
3 تعداد مکعب های کوچک 1×1×1 را در هر شکل با یک عدد توان دار نشان دهید.
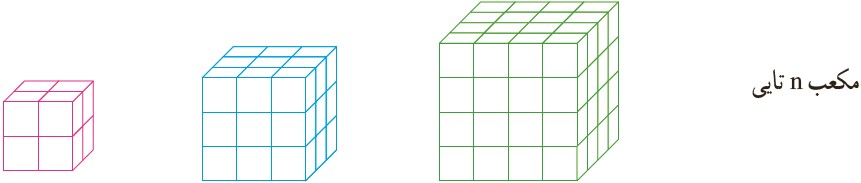
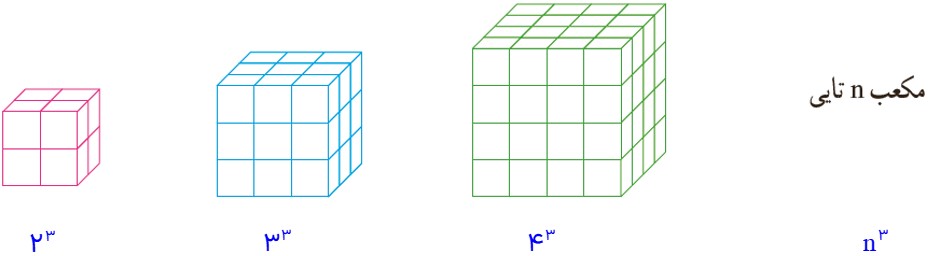
4 حاصل هر عبارت تواندار را به دست آورید.
\(\begin{array}{l}{3^2} = \\\\{4^2} = \\\\{5^2} = \\\\{6^2} = \\\\{7^2} = \\\\{8^2} = \\\\{9^2} = \\\\{10^2} = \\\\{11^2} = \\\\{12^2} = \end{array}\)
مجذور دو =
مجذور یک =
مکعب دو =
مکعب یک =
\(\begin{array}{l}\frac{{{2^3}}}{{{5^2}}} = \\\\{\left( {\frac{3}{4}} \right)^3} = \\\\\frac{{{2^4}}}{7} = \\\\0/{2^2} = \\\\0/{01^2} = \\\\1/{1^2} = \\\\2/{1^2} = \\\\0/{5^2} = \end{array}\)
\(\begin{array}{l}{3^2} = 3 \times 3 = 9\\\\{4^2} = 4 \times 4 = 16\\\\{5^2} = 5 \times 5 = 25\\\\{6^2} = 6 \times 6 = 36\\\\{7^2} = 7 \times 7 = 49\\\\{8^2} = 8 \times 8 = 64\\\\{9^2} = 9 \times 9 = 81\\\\{10^2} = 10 \times 10 = 100\\\\{11^2} = 11 \times 11 = 121\\\\{12^2} = 12 \times 12 = 144\end{array}\)
\( = {2^2} = 2 \times 2 = 4\) مجذور دو
\( = {1^2} = 1 \times 1 = 1\) مجذور یک
\( = {2^3} = 2 \times 2 \times 2 = 8\) مکعب دو
\( = {1^3} = 1 \times 1 \times 1 = 1\) مکعب یک
\(\begin{array}{l}\frac{{{2^3}}}{{{5^2}}} = \frac{{2 \times 2 \times 2}}{{5 \times 5}} = \frac{8}{{25}}\\\\{\left( {\frac{3}{4}} \right)^3} = \frac{3}{4} \times \frac{3}{4} \times \frac{3}{4} = \frac{{27}}{{64}}\\\\\frac{{{2^4}}}{7} = \frac{{2 \times 2 \times 2 \times 2}}{7} = \frac{{16}}{7}\\\\0/{2^2} = 0/2 \times 0/2 = 0/04\\\\0/{01^2} = 0/01 \times 0/01 = 0/0001\\\\1/{1^2} = 1/1 \times 1/1 = 1/21\\\\2/{1^2} = 2/1 \times 2/1 = 4/41\\\\0/{5^2} = 0/5 \times 0/5 = 0/25\end{array}\)
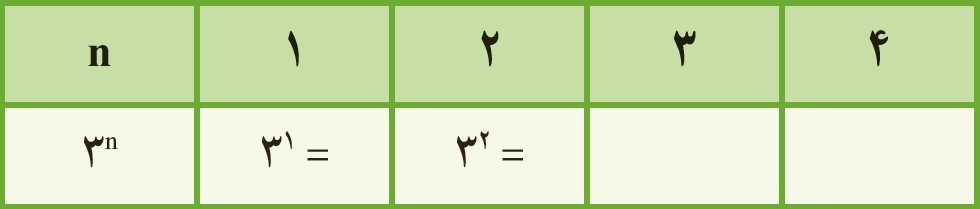
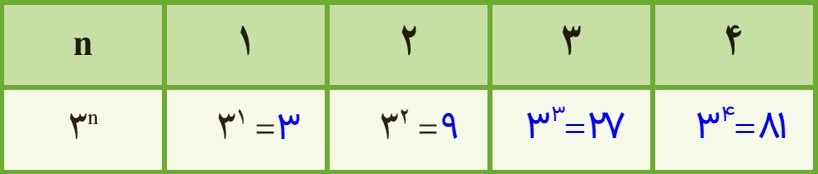
5 مقدار عبارت \({3^n}\) را به ازای عددهای داده شده به دست آورید.
6 حاصل عددهای \(2{\,^5}\,,\,2{\,^4}\,,\,2{\,^3}\,,\,2{\,^2}\,,\,2{\,^1}\) را به دست آورید و به صورت نمودار ستونی در دفتر خود رسم کنید (باید واحد مناسبی برای محور عمودی رسم کنید.) در مورد شیوهٔ رسم هر ستون توضیح دهید. آیا می توانید \(2{\,^6}\) یا \(2{\,^7}\) را در دفتر خود رسم کنید؟ چرا؟
\(\begin{array}{l}2{\,^1} = 2\\\\2{\,^2} = 4\\\\2{\,^3} = 8\\\\2{\,^4} = 16\\\\2{\,^5} = 32\end{array}\)
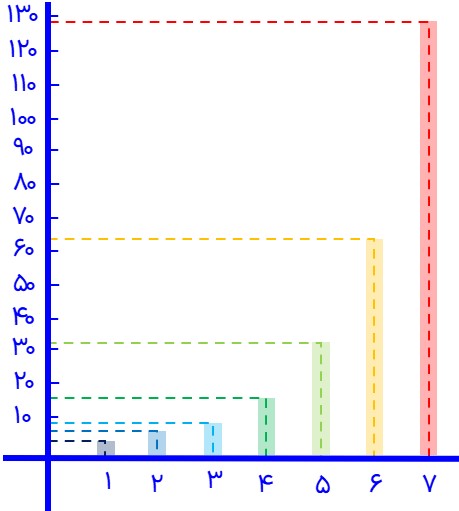
با دقت در ستون های نمودار متوجه می شویم که هر ستون دو برابر ستون قبلی است. با این شرایط \(2{\,^6}\) دو برابر \(2{\,^5}\) است، همچنین \(2{\,^7}\) دو برابر \(2{\,^6}\) می باشد.
7 عدد \(11{\,^{12}}\) به طور تقریبی چندرقمی است؟ چرا؟
\(\begin{array}{l}11{\,^{12}} \simeq 10{\,^{12}} = 10 \times 10 \times \cdots \times 10\\\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,1,000,000,000,000\end{array}\)
این عدد 13 رقمی می باشد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















