گام به گام فعالیت صفحه 91 درس 7 ریاضی هفتم (توان و جذر)

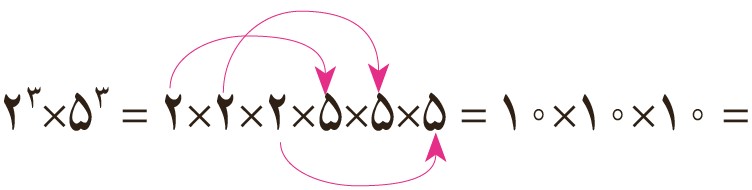
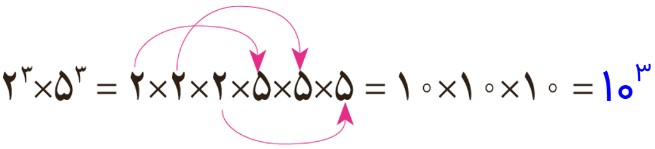
\(\begin{array}{l}{3^2} \times {4^2} = 3 \times 3 \times 4 \times 4 = \\\\(3 \times 4) \times (3 \times 4) = 12 \times 12 = {12^2}\end{array}\)

\(\begin{array}{l}{\left( {\frac{2}{7}} \right)^3} \times {5^3} = \\\\\left( {\frac{2}{7}} \right) \times \left( {\frac{2}{7}} \right) \times \left( {\frac{2}{7}} \right) \times 5 \times 5 \times 5 = \\\\\left( {\frac{2}{7} \times 5} \right) \times \left( {\frac{2}{7} \times 5} \right) \times \left( {\frac{2}{7} \times 5} \right) = \\\\\left( {\frac{{10}}{7}} \right) \times \left( {\frac{{10}}{7}} \right) \times \left( {\frac{{10}}{7}} \right) = {\left( {\frac{{10}}{7}} \right)^3}\end{array}\)

\(\begin{array}{l}{a^2} \times {b^2} = a \times a \times b \times b = \\\\(a \times b) \times (a \times b) = {(a \times b)^2} = {(ab)^2}\end{array}\)

\(\begin{array}{l}{x^4} \times {y^4} = \\\\x \times x \times x \times x \times y \times y \times y \times y = \\\\(x \times y) \times (x \times y) \times (x \times y) \times (x \times y) = \\\\{(x \times y)^4} = {(xy)^4}\end{array}\)

اگر توان ها مساوی بودند، یکی از توان ها را می نویسیم و سپس پایه ها را در هم ضرب می کنیم.

\({2^4} \times {3^4} = {(2 \times 3)^4} = {6^4}\)

\({\left( {\frac{2}{3}} \right)^6} \times {\left( {\frac{3}{4}} \right)^6} = {\left( {\frac{2}{3} \times \frac{3}{4}} \right)^6} = {\left( {\frac{1}{2}} \right)^6}\)

\({\left( {\frac{1}{2}} \right)^5} \times {3^5} = {\left( {\frac{1}{2} \times 3} \right)^5} = {\left( {\frac{3}{2}} \right)^5}\)

\(\begin{array}{l}{\left( { - 2} \right)^7} \times {\left( { - 1} \right)^7} = {\left( {\left( { - 2} \right) \times \left( { - 1} \right)} \right)^7} = \\\\{2^7}\end{array}\)

\({\left( { - 2} \right)^5} \times {3^5} = {\left( {\left( { - 2} \right) \times 3} \right)^5} = {\left( { - 6} \right)^5}\)

\({x^2} \times {y^2} = {(x \times y)^2} = {(xy)^2}\)

\(\begin{array}{l}{15^7} = {(3 \times 5)^7} = {3^7} \times {5^7}\\\\{10^4} = {(2 \times 5)^4} = {2^4} \times {5^4}\\\\{12^8} = {(3 \times 4)^8} = {3^8} \times {4^8}\\\\{\left( {xy} \right)^{10}} = {x^{10}} \times {y^{10}}\\\\{\left( {xyz} \right)^4} = {x^4} \times {y^4} \times {z^4}\\\\{30^5} = {(5 \times 6)^5} = {5^5} \times {6^5}\end{array}\)