درسنامه کامل ریاضی هشتم فصل 2 عددهای اول
تعداد بازدید : 7.59Mخلاصه نکات ریاضی هشتم فصل 2 عددهای اول - درسنامه شب امتحان ریاضی هشتم فصل 2 عددهای اول - جزوه شب امتحان ریاضی هشتم نوبت اول فصل 2 عددهای اول
تشخیص اول یا مرکب بودن هر عدد طبیعی
تشخیص اول یا مرکب بودن هر عدد طبیعی
مطابق روش غربال باید مشخص شود عدد مورد نظر مضرب عدد های اول می باشد یا خیر. برای تشخیص ، باید عدد مورد نظر را بر اعداد اول مانند ... و 7 و 5 و 3 و 2 تقسیم کرد:
الف) اگر عدد داده شده بر یکی یا بیشتر ، از اعداد اول بخش پذیر باشد (باقیمانده صفر شود)، عدد داده شده مرکب است.
ب) اگر عدد داده شده بر هیچ کدام از اعداد اول بخش پذیر نباشد (باقیمانده صفر نشود)، عدد داده شده اول است.
برای تعیین تعداد این تقسیم ها ، از عدد مورد نظر جذر تقریبی می گیریم و سپس عدد داده شده را بر اعداد اول کوچکتر از جذر تقسیم می کنیم.
مثال
می خواهیم مشخص کنیم عدد 37 ، عدد اول است یا مرکب؟
ابتدا جذر تقریبی عدد 37 را می گیریم \((6 = \sqrt {36} < \sqrt {37} < \sqrt {49} = 7 \Rightarrow \sqrt {37} \simeq 6/1)\)
پس 37 را بر اعداد اول کوچکتر از 6 (یعنی 2، 3 و 5) تقسیم می کنیم:
یکان 37 فرد است پس بر 2 بخش پذیر نیست.
مجموع ارقام 37 عدد 10 است و بر 3 بخش پذیر نیست.
یکان 7 است و بر 5 بخش پذیر نیست (یکانش صفر یا 5 نیست).
چون بر هیچ کدام از اعداد اول 2 و 3 و 5 بخش پذیر نیست، بنابراین 37 یک عدد اول است.
مشخص کنید عدد 93 اول است یا مرکب؟
ابتدا جذر تقریبی عدد 93 را محاسبه می کنیم:
\(9 = \sqrt {81} < \sqrt {93} < \sqrt {100} = 10 \Rightarrow \sqrt {93} \simeq 9/6\)
پس عدد 93 را بر عددهای اول کوچکتر از 9 (یعنی 2، 3، 5 و 7) تقسیم می کنیم:
یکان 93 فرد است پس بر 2 بخش پذیر نیست.
مجموع ارقام 93 عدد 12 است و بر 3 بخش پذیر است.
عدد 93 بر 3 بخش پذیر است، پس 93 یک عدد مرکب است.
عددی کمتر از 160 و بزرگتر از 130 می باشد. برای اینکه بفهمیم این عدد اول است یا خیر، حداکثر چند تقسیم انجام می دهیم؟ چرا؟
در اینجا چون عدد مورد نظر دقیقا مشخص نشده باید عدد بزرگتر در صورت سوال مد نظر قرار گیرد.
\(12 = \sqrt {144} < \sqrt {160} < \sqrt {169} = 13 \Rightarrow \sqrt {160} \simeq 12/6\)
پس بر اعداد اول کوچکتر از 12 باید تقسیم شود. یعنی بر 2 و 3 و 5 و 7 و 11 پس یعنی حداکثر 5 تقسیم.
توجه کنید که در تمرین بالا، فقط تعداد تقسیم ها پرسیده شده و هیچ تقسیمی انجام نمی شود زیرا عدد مورد نظر دقیقاً داده نشده است.
عددهای 1 تا 90 را نوشته و غربال کرده ایم. با توجه به آن به سوالات زیر پاسخ دهید:
الف اولین عددی که خط می خورد؟
عدد 1
ب اولین مضرب مرکب 7 که برای اولین بار خط می خورد؟
عدد 49
پ عدد 57 با مضرب کدام عدد خط می خورد؟
عدد 3
ت تمام مضرب های 5 که برای بار اول خط می خورند، را بنویسید.
25 – 35 – 55 – 65 – 85
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
یادآوری
شمارنده (مقسوم علیه) یک عدد
شمارنده ها همان اعدادی هستند که عدد داده شده بر آنها بخش پذیر می شود؛ به عنوان مثال شمارنده های عدد 15، اعداد 1، 3، 5 و 15 هستند.
عدد اول
هر عدد طبیعی بزرگتر از یک که هیچ شمارنده طبیعی به جز خودش و یک نداشته باشد، عدد اول نامیده می شود؛ مانند اعداد 5 و 7:
شمارنده های 5، اعداد 1 و 5 هستند.
5 = 5 × 1
شمارنده های 7، اعداد 1 و 7 هستند.
7 = 7 × 1
عدد مرکب
هر عدد طبیعی بزرگتر از یک که بتوان آن را به صورت حاصل ضرب دو عدد طبیعی بزرگتر از یک نوشت ، عدد مرکب می نامند؛ مانند اعداد 30 و 6:
شمارنده های عدد 30:
15 × 2 = 10 × 3 = 6 × 5 = 30
شمارنده های عدد 6:
3 × 2 = 6
1 عدد یک، نه اول است و نه مرکب. ( زیرا فقط یک شمارنده دارد؛ یعنی خود یک)
2 هر عدد اول دقیقا دو شمارنده دارد.
3 هر عدد مرکب بیش از دو شمارنده دارد.
4 عدد یک، شمارنده ی همه عددهای طبیعی است.
5 بزرگترین شمارنده هر عدد، خود عدد است.
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم فصل 1 عددهای صحیح و گویا
جزوه جامع ریاضی هشتم فصل 2 عددهای اول
جزوه جامع ریاضی هشتم فصل 3 چندضلعی ها
جزوه جامع ریاضی هشتم فصل 4 جبر و معادله
جزوه جامع ریاضی هشتم فصل 5 بردار و مختصات
جزوه جامع ریاضی هشتم فصل 6 مثلث
جزوه جامع ریاضی هشتم فصل 7 توان و جذر
جزوه جامع ریاضی هشتم فصل 8 آمار و احتمال
جزوه جامع ریاضی هشتم فصل 9 دایره
مضرب های طبیعی یک عدد
مضرب های طبیعی یک عدد
برای نوشتن مضرب های طبیعی یک عدد ، کافی است عدد داده شده را به ترتیب در اعداد طبیعی ضرب کنیم تا مضرب های طبیعی آن بدست بیاید.
مثال
مضرب های طبیعی عددهای زیر را بنویسید.
مضرب های طبیعی 5
مضرب های طبیعی 6
مضرب های طبیعی 5 \( = 1 \times 5\,,\,2 \times 5\,,\,3 \times 5\,,\,4 \times 5\,,\, \cdots = 5\,,\,10\,,\,15\,,\,20\)
مضرب های طبیعی 6\( = 6\,,\,12\,,\,18\,,\,24\,,\,30\,,\,36\,,\, \cdots \)
با توجه به مثال بالا می توان نکته های زیر را نتیجه گرفت:
1 فقط اولین مضرب هر عدد اول ، عددی اول است و بقیه مضرب های آن مرکب هستند؛ مثلا 5 عددی اول است پس اولین مضرب آن یعنی خود 5 ، اول و بقیه مضرب های آن یعنی ...و 20 و 15 و 10 مرکب هستند.
2 همه مضرب های یک عدد مرکب ، مرکب هستند؛ مثلاً 6 عددی مرکب است پس همه مضرب های آن مرکب هستند.
به این ترتیب، اعداد طبیعی به سه بخش تقسیم می شوند:
1 عدد 1
2 عددهای اول
3 عددهای مرکب
مثال
الف عدد 10 چند مضرب دارد؟
بی شمار
ب چند تا از مضرب های آن عدد اول هستند؟
هیچ کدام؛ زیرا خود 10 عددی مرکب است،پس همه مضرب های آن نیز مرکب اند.
پ تنها مضرب اول عدد 23 کدام است؟
خود عدد 23
تعداد شمارنده های یک عدد محدود است اما تعداد مضرب های آن بی شمار!
دو عدد متباین (نسبت به هم اول)
اگر ب.م.م (بزرگترین مقسوم علیه مشترک) دو عدد برابر یک باشد، می گوییم دو عدد نسبت به هم اول هستند؛ به عنوان مثال عدد های 6 و 35 نسبت به هم اول هستند؛ زیرا:
مضرب های طبیعی 5\( = 1\,,\,5\,,\,7\,,\,35\)
مضرب های طبیعی 6\( = 1\,,\,2\,,\,3\,,\,6\)
\( \Rightarrow (35\,,\,6) = 1\)
1 هر دو عدد اول متمایز نسبت به هم اول هستند؛ مانند: \((23\,,\,11) = 1\)
2 هر دو عدد طبیعی متوالی نسبت به هم اول هستند؛ مانند: \((31\,,\,32) = 1\)
3 عدد یک و هر عدد طبیعی بزرگتر از یک نسبت به هم اول هستند؛ مانند: \((25\,,\,1) = 1\)
4 اگر دو عدد طبیعی نسبت به هم اول باشند ، ک.م.م (کوچکترین مضرب مشترک) آنها از حاصل ضرب آن دو عدد بدست می آید؛ مثلا 1 = (3 و 4)؛ آن گاه ک.م.م آن دو برابر است با:
\([4\,,\,3] = 4 \times 3 = 12\)
مثال
الف سه عدد مرکب بنویسید که غیر از 2 و 7 شمارنده اول دیگری نداشته باشند.
چون 2 و 7 هر دو شمارنده های اول این اعداد هستند پس باید آنها را در هم ضرب کنیم و چون غیر از 2 و 7 شمارنده اول دیگری ندارند، پس برای ساخت عدد های بعدی باید به تعداد دلخواه 2 و 7 را در هم ضرب کنیم.
\(\begin{array}{l}2 \times 7 = 14\\\\2 \times 2 \times 7 = 28\\\\2 \times 2 \times 2 \times 7 = 56\\\\2 \times 7 \times 7 = 98\end{array}\)
ب آیا این عددها نسبت به عددی که شمارنده های اول آن 7 و 13 باشند، اول است ؟
خیر؛ زیرا شمارنده مشترک 7 را دارند؛ پس نسبت به هم اول نیستند.
مثال
اگر تعداد عدد های اول کمتر از 35، 11 عدد باشند، تعداد عددهای مرکب کمتر از 35 چند تا است؟ چرا؟
عددهای طبیعی سه بخش می شوند: یک، عدد اول، عدد مرکب. در اینجا از 35 عدد، 11 عدد اول هستند و یکی دیگر از آن 35 عدد، عدد یک است (که نه اول است و نه مرکب). در نتیجه (12 = 11 + 1) 12 عدد از 35 عدد مرکب نیستند؛ پس تعداد عدد های مرکب کمتر از 35:
23 = 12 – 35
مجموع دو عدد اول، 25 است. حاصل ضرب آن دو عدد را بدست آورید.
هرگاه مجموع یا تفاضل دو عدد طبیعی ، عددی فرد باشد یکی از آنها زوج و دیگری فرد بوده است. در اینجا چون ذکر شده مجموع دو عدد اول ،پس می نویسیم: (25 = عدد زوج اول + عدد فرد اول) و چون تنها عدد زوج اول عدد 2 می باشد؛ پس داریم:
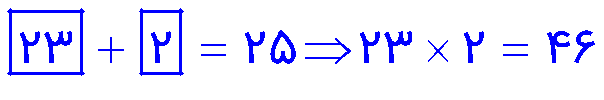
عددهای 15 و 21 دو شمارنده یک عدد هستند. شش شمارنده دیگر این عدد را بنویسید.
\(\left\{ \begin{array}{l}15 = 3 \times 5\\\\21 = 3 \times 7\end{array} \right. \Rightarrow \,5 \times 7 = 35\,\,\,,\,\,\,3 \times 5 \times 7 = 105\)
دیگر شمارنده ها:
105، 35، 7، 5، 3، 1
توجه کنید که یک شمارنده همه عدد ها است و چون در ساختار 15 و 21 عدد های 3 و 5 و 7 وجود دارد پس در واقع در ساختار عدد اصلی هم باید وجود داشته باشند و در نهایت حاصل ضرب این عددها (یعنی 3 و 5 و 7) نیز در ساختار عدد اصلی وجود دارد.
یادآوری چند قاعده بخش پذیری
یادآوری چند قاعده بخش پذیری
1- بخش پذیری بر 2:
عددی بر 2 بخش پذیر است که رقم یکان آن 0 و 2 و 4 و 6 و 8 باشد. (یا زوج باشد)
2- بخش پذیری بر 3:
عددی بر 3 بخش پذیر است که مجموع ارقامش بر 3 بخش پذیر باشد.
3- بخش پذیری بر 5:
عددی بر 5 بخش پذیر است که رقم یکان آن 0 یا 5 باشد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
غربال
روش غربال
برای تعیین عددهای اول از روش غربال استفاده می کنیم. در این روش، در واقع عددهای غیر اول را خط می زنیم تا عددهای اول باقی بمانند. به این ترتیب که:
1) ابتدا عدد یک را خط می زنیم. (زیرا یک نه اول است و نه مرکب)
2) عدد 2، اول است و همه مضرب های آن به جز خود 2، مرکب هستند. پس همه اعداد زوج به غیر از عدد 2 را خط می زنیم.
3) عدد 3، اول است. تمام مضرب های عدد 3 را، به جز خود 3 خط می زنیم.
و به همین ترتیب خط زدن را تا عدد اولی که مربع (توان دوم) آن بین عدد های نوشته شده نباشد، ادامه می دهیم.
دقت کنید
در اینجا اولین مضرب مرکب هر عدد اول که برای اولین بار خط می خورد، توان دوم آن عدد اول است؛ مثلا اولین مضرب مرکب 5 که برای اولین بار خط می خورد، \({5^2} = 25\) می باشد و در نهایت اعداد خط نخورده باقی مانده، اول هستند.
مثال
می خواهیم عدد های اول بین 1 تا 30 را بیابیم.
1 ابتدا عدد یک خط می خورد:

2 عدد 2 اول است پس اولین مضرب مرکب 2 که خط می خورد، مربع 2 یعنی 4 می باشد و بعد از آن می توان گفت بقیه ی مضرب های مرکب 2 را به صورت 2 تا 2 تا بعد از 4 خط می زنیم. (بعنی ... و 8 و 6 و 4)
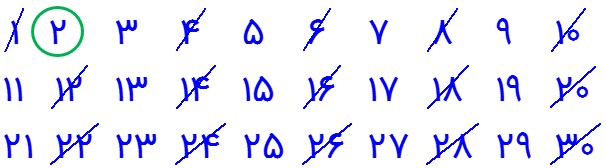
3 عدد 3 اول است و مضرب های مرکب آن که هنوز خط نخورده اند را با شروع از 9 (یعنی مربع عدد 3) به صورت 3 تا 3 تا خط می زنیم.
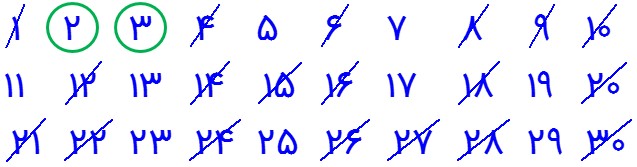
4 خط زدن را تا مربع عدد 5 ، یعنی 25 ادامه می دهیم. زیرا بعد از آن ، مربع عدد 7 را داریم که 49 می شود و چون 49 از 30 بزرگتر است پس کار خط زدن عدد های مرکب تمام می شود و عدد های باقیمانده که دورشان خط کشیده شده، همه اول هستند.

عددهای اول بین 30 تا 50 را با روش غربال بنویسید.
راهنمایی:
دقت کنید در اینجا ابتدای کار ما عدد یک نیست . در نتیجه قطعا اولین مضرب عدد اول 2 هم که خط می خورد عدد 4 نیست. در این سوال ها می توانید از قوانین بخشپذیری برای یافتن اولین مضرب مرکب عدد اول (در اینجا عدد 2) استفاده کنید.
توجه داشته باشید که در این سوال ها هم برای بعضی از عدد های اول ، اولین مضرب مرکب همان توان دوم عدد اول است. در اینجا اولین مضرب 2 که خط می خورد عدد 32 می باشد.
1 مضرب های عدد اول 2 را خط می زنیم. زیرا: \({2^2} = 4 < 49\)
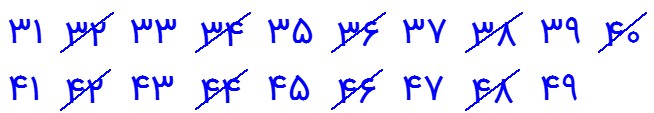
در اینجا اولین مضرب 3 که خط می خورد عدد 33 می باشد.
2 مضرب های عدد اول 3 را خط می زنیم؛ زیرا: \({3^2} = 9 < 49\)
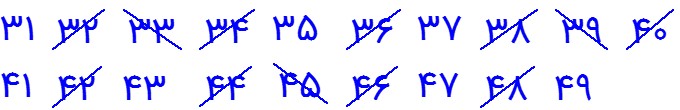
در اینجا اولین مضرب 5 که خط می خورد عدد 35 می باشد.
3 مضرب های عدد اول 5 را خط می زنیم؛ زیرا: \({5^2} = 25 < 49\)
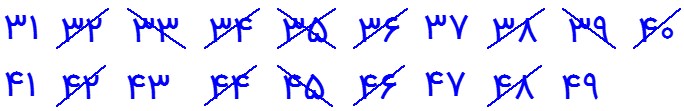
در اینجا اولین مضرب 7 که خط می خورد همان مربع عدد 7 یعنی 49 می باشد و چون مربع عدد اول بعدی یعنی 11، 121 می شود و از 49 بزرگتر است پس کار خط زدن تمام می شود.
4 مضرب های اول 7 را خط می زنیم . زیرا \({7^2} = 49\) و اعداد باقیمانده همان اعداد اول در فاصله 30 تا 50 می باشند.




1736019749.png)















