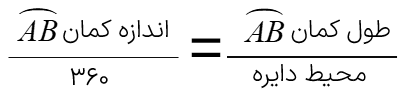درسنامه کامل ریاضی هشتم فصل 9 دایره
تعداد بازدید : 7.59Mخلاصه نکات ریاضی هشتم فصل 9 دایره - درسنامه شب امتحان ریاضی هشتم فصل 9 دایره - جزوه شب امتحان ریاضی هشتم نوبت اول فصل 9 دایره
خط و دایره
دایره
مکان هندسی تمام نقاطی از صفحه است که از یک نقطه به نام مرکز دایره به یک فاصله است. این فاصله شعاع دایره نامیده میشود.
فاصله یک نقطه از یک خط کوتاه ترین فاصله طول پاره خطی است که از آن نقطه بر خط عمود می شود.
وضعیت خط و دایره
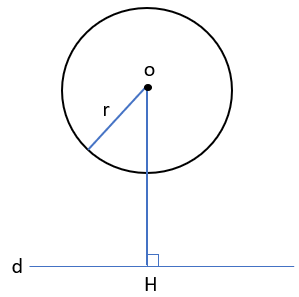
۱) خط خارج از دایره است.
2)\(r < OH\)
(3خط و دایره هیچ نقطه مشترکی ندارند.
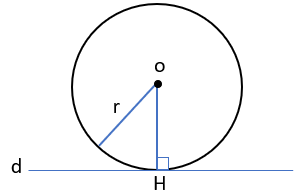
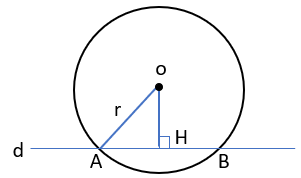
1) خط بر دایره مماس است.
2)\(r = OH\)
3)خط و دایره یک نقطه مشترک دارند.
۱) خط از داخل دایره میگذرد.
2)\(OH < r\)
۳) خط و دایره دو نقطه مشترک دارند
۱ شعاع دایره در نقطه تماس بر خط مماس عمود است.
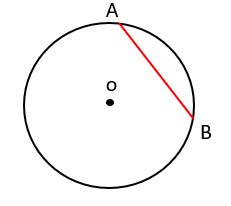
2 وتر ،دایره پاره خطی است که دو سر یک کمان را به هم وصل می کند.
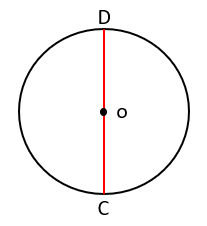
3بزرگترین وتر،دایره قطر دایره است که از مرکز آن می گذرد و دایره را به دو کمان مساوی ۱۸۰ درجه تقسیم می کند. \(\overline {CD} \)وتر = قطر دایره
تهیه کنندگان:سمیه انصاری-عبدالهادی آرامی-عبدالله بهزادی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
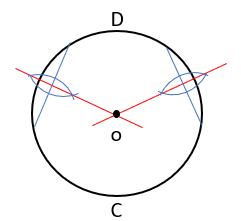
تعیین مرکز دایره
تعیین مرکز دایره
دو وتر غیر موازی رسم کرده و سپس عمود منصف هر دو وتر را رسم می کنیم. محل برخورد دو عمود منصف مرکز دایره است (O مرکز دایره است(
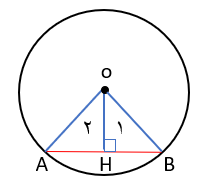
نشان دهید اگر خطی از مرکز دایره بر وتر عمود ،شود آن را به دو قسمت مساوی تقسیم می کند. (O مرکز دایره است(.
فرض مسئله(شعاع دایره) OA = OB
ضلع مشترک OH = OH
به حالت وتر و یک ضلع داریم:
\(\left. \begin{array}{l}\overline {OA} = \overline {OB} \\\\\overline {OH} = \overline {OH} \end{array} \right\} \Rightarrow A\mathop O\limits^\Delta H \cong B\mathop O\limits^\Delta H\)
بنابراین\( \leftarrow \)AH = HB
در نتیجه اگر خطی از مرکز دایره بر وتر عمود شود آن را به دو قسمت مساوی تقسیم می کند.
\(\widehat {{H_1}} = \widehat {{H_2}} = 90 \to \overline {AH} = \overline {HB} \)
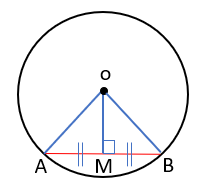
نشان دهید اگر خطی از مرکز دایره به وسط وتر رسم کنیم بر آن وتر عمود می شود (O مرکز دایره است(.
\(\widehat {{M_1}} = \widehat {{M_2}} = 90^\circ \)
شعاع دایرهOA = OB
فرض مسئلهAM = MB
ضلع مشترک OM = OM
بنا به حالت (ض ض ض)داریم:
\(\left. \begin{array}{l}\overline {OA} = \overline {OB} \\\overline {OM} = \overline {OM} \\\overline {AM} = \overline {MB} \end{array} \right\} \Rightarrow A\mathop O\limits^\Delta M \cong B\mathop O\limits^\Delta M\)
بنابراین\({M_1} = {M_2} = 90 \leftarrow \)
در نتیجه اگر خطی از مرکز دایره به وسط یک وتر رسم کنیم بر آن وتر عمود میشود.
\(\overline {AM} = \overline {MB} \to {M_1} = {M_2} = 90\)
فاصله مرکز دایره از وتر طول پاره خطی است که از مرکز دایره بر وتر عمود شده وآن را نصف میکند.
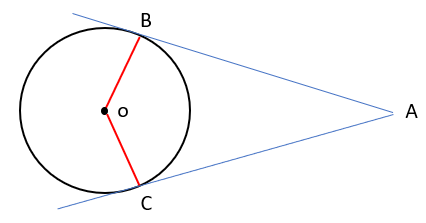
از هر نقطه خارج از دایره دو مماس میتوان بر دایره رسم کرد که طول هر دو مماس با هم برابراست.
تهیه کنندگان:سمیه انصاری-عبدالهادی آرامی-عبدالله بهزادی
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم فصل 1 عددهای صحیح و گویا
جزوه جامع ریاضی هشتم فصل 2 عددهای اول
جزوه جامع ریاضی هشتم فصل 3 چندضلعی ها
جزوه جامع ریاضی هشتم فصل 4 جبر و معادله
جزوه جامع ریاضی هشتم فصل 5 بردار و مختصات
جزوه جامع ریاضی هشتم فصل 6 مثلث
جزوه جامع ریاضی هشتم فصل 7 توان و جذر
جزوه جامع ریاضی هشتم فصل 8 آمار و احتمال
جزوه جامع ریاضی هشتم فصل 9 دایره
زاویه مرکزی
زاویه مرکزی
زاویه مرکزی زاویه ای است که رأس آن روی مرکز دایره و اضلاع آن شعاع های دایره هستند.اندازه زاویه مرکزی برابر است با اندازه کمان روبروی آن.\(\widehat {{O_1}} = AB\)
یک رابطه مهم:
مثال
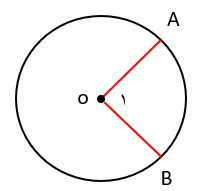
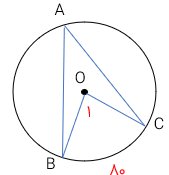
اگر \(\overline {OB} = 1cm\) باشد طول کمان AB چقدر است؟
محیط دایره: \( \Rightarrow 2\pi r = 1 \times 2 \times \pi = 2\pi \)
\(\frac{{60}}{{360}} = \frac{x}{{\pi 2}} \to x = \frac{{60 \times 2\pi }}{{360}} = \frac{\pi }{3}\)
مثال
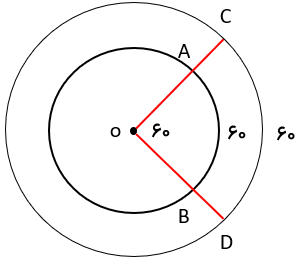
اگر \(\overline {OD} = 2cm\) ،باشد طول کمان CD چقدر است؟
محیط دایره: \( \Rightarrow 2 \times 2 \times \pi = 4\pi \)
\(\frac{{60}}{{360}} = \frac{x}{{\pi 4}} \to x = \frac{{60 \times 4\pi }}{{360}} = \frac{{2\pi }}{3}\)
تهیه کنندگان:سمیه انصاری-عبدالهادی آرامی-عبدالله بهزادی
طریقه رسم اشکال مختلف
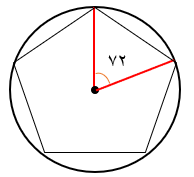
طریقه رسم پنج ضلعی منتظم
ابتدا ۳۶۰ را تقسیم بر ۵ کرده و اندازه زاویه مرکزی ۵ضلعی منتظم را به دست می آوریم. \(\left( {\frac{{360}}{5} = 72} \right)\) حال زاویه مرکزی ۷۲ درجه را رسم می کنیم دهانه پرگار را به اندازه کمان ۷۲ درجه باز کرده و سوزن پرگار را روی یکی از نقاط برخورد اضلاع زاویه با محیط دایره قرار داده و کمان های پی در پی میزنیم حال نقاط ایجاد شده را به هم وصل می کنیم.
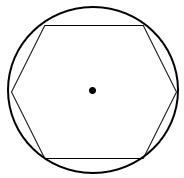
طریقه رسم شش ضلعی منتظم
دهانه پرگار را به اندازه شعاع موردنظر باز کرده و از یک نقطه دلخواه روی محیط دایره کمان های پی در پی میزنیم بدین ترتیب دایره به ۶ کمان مساوی تقسیم میشود. حال نقاط به دست آمده را به هم وصل می کنیم.
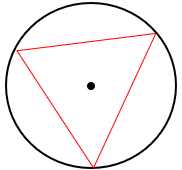
طریقه رسم سه ضلعی منتظم
مانند آنچه برای شش ضلعی منتظم بود عمل می کنیم ولی نقاط به دست آمده را یکی در میان به هم وصل میکنیم.
طریقه رسم هشت ضلعی منتظم
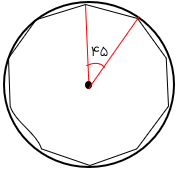
ابتدا ۳۶۰ را بر ۸ تقسیم کرده و اندازه زاویه مرکزی۸ ضلعی منتظم را به دست می آوریم\(\left( {\frac{{360}}{8} = 45} \right)\) دهانه پرگار را به اندازه کمان ۴۵درجه باز کرده و از یک نقطه دلخواه کمان های پی در پی میزنیم حال نقاط ایجاد شده را به هم وصل می کنیم.
1 برای رسم هر 11 ضلعی منتظم مشابه روش های بالا عمل میکنیم
2 وترهای نظیر کمانهای مساوی با یکدیگر برابر میباشند.\(AB = CD = \overline {AB} = \overline {CD} \)
3کمان های نظیر وترهای مساوی با یکدیگر برابر هستند.\(\overline {AB} = \overline {CD} = AB = CD\)
4قطر دایره دایره را به دو کمان ۱۸۰ درجه تقسیم میکند.
5 محیط ،دایره برابر ۳۶۰ درجه است.
تهیه کنندگان:سمیه انصاری-عبدالهادی آرامی-عبدالله بهزادی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
زاویه محاطی
زاویه محاطی
زاویه محاطی به زاویه ای گفته میشود که رأس آن روی محیط دایره و اضلاع آن وترهای دایره باشند.
با توجه به مرکز دایره و وضعیت قرار گرفتن وترها نسبت به مرکز دایره سه نوع زاویه محاطی می توانیم ایجاد کنیم.
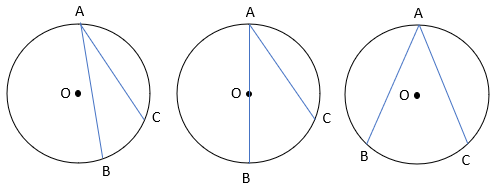
اندازه زاویه محاطی نصف کمان روبروی آن است.\(\widehat A = \frac{{\widehat {BC}}}{2}\)
مثال
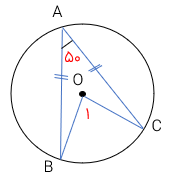
در شکل مقابل اندازه زاویه های خواسته شده را به دست آورید.
\(\begin{array}{l}\widehat A = ?\\\widehat {{O_1}} = ?\end{array}\)
\(\begin{array}{l}\widehat A = 40^\circ \\\widehat {{O_1}} = 80^\circ \end{array}\)
مثال
در شکل مقابل اندازه زاویه های خواسته شده را به دست آورید.
\(\begin{array}{l}\widehat {{O_1}} = ?\\AB = ?\\BC = ?\end{array}\)
\(\begin{array}{l}\widehat {{O_1}} = 100^\circ \\AB = 130^\circ \\BC = 100^\circ \end{array}\)
1بیشمار زاویه محاطی رو به روی یک کمان وجود دارد.
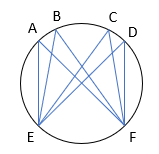
2 زوایای محاطی رو به روی یک کمان با هم برابرند.
\(\widehat A = \frac{{EF}}{2},\widehat B = \frac{{EF}}{2},\widehat C = \frac{{EF}}{2},\widehat D = \frac{{EF}}{2} \Rightarrow \widehat A = \widehat B = \widehat C = \widehat D\)
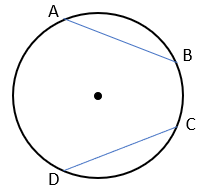
3 به چهارضلعی که چهار رأس آن روی محیط دایره باشد چهارضلعی محاطی گفته می شود و زاویه های روبرو در این چهارضلعی مکمل یکدیگرند.
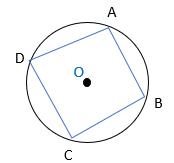
\(\begin{array}{l}\widehat A + \widehat C = 180^\circ \\\widehat B + \widehat D = 180^\circ \end{array}\)
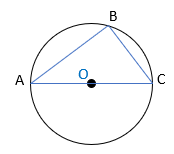
4 زاویه محاطی رو به روی قطر ۹۰ درجه است.
\(\widehat B = \frac{{AC}}{2} = \frac{{180^\circ }}{2} = 90^\circ \)
تهیه کنندگان:سمیه انصاری-عبدالهادی آرامی-عبدالله بهزادی



1736019749.png)