درسنامه کامل ریاضی هشتم فصل 4 جبر و معادله
تعداد بازدید : 7.27Mخلاصه نکات ریاضی هشتم فصل 4 جبر و معادله - درسنامه شب امتحان ریاضی هشتم فصل 4 جبر و معادله - جزوه شب امتحان ریاضی هشتم نوبت اول فصل 4 جبر و معادله
عبارات جبری
عبارات جبری
هر ترکیبی از عدد یا حروف که به وسیله ی عمل های جبری مانند جمع، تفریق، ضرب و تقسیم به هم مربوط شوند. مانند:
\(5x\,,\,\frac{2}{{3a}}\,,\,9{a^2} - 4c\)
در یک جمله ای ها علامت ضرب بین عدد و حروف، یا ضرب بین حروف را نمی نویسیم یا اگر هم بخواهیم علامت ضرب قرار دهیم با یک نقطه بین حروف، یا با قرار دادن آن ها در پرانتز نشان می دهند.
انواع عبارت های جبری
1- یک جمله ی جبری:
اگر در یک عبارت جبری بین حروف و اعداد فقط از علامت ضرب استفاده شود، آنگاه تشکیل جمله ای می دهد. مانند:
\(2{x^2}\,,\,8{a^3}b\)
2- چند جمله ی جبری:
اگر دو یا چند، یک جمله ای غیرمتشابه را با هم جمع یا تفریق کنیم، آنگاه تشکیل یک چند جمله ای جبری می دهد؛ مانند:
(سه جمله ای) 2a-6+4x
(دو جمله ای) -3a+5b
1هر عدد به توان یک برابر با خودش است:
\({x^1} = x\)
2 یک به توان هر عدد دلخواه، برابر با یک است:
\({1^x} = 1\)
3صفر به توان هر عدد مثبت برابر صفر می شود:
\({0^x} = 0\,\,\,\,\,\,\,\,\,(x > 0)\)
4سه عدد غیرصفر به توان صفر برابر یک می شود:
\({x^0} = 1\,\,\,\,\,\,\,\,\,\,\,\,(x \ne 0)\)
5در ضرب دو عبارت توان دار با پایه های مساوی، یک پایه را نوشته و توان ها را با هم جمع می کنیم:
\({x^a} \times {x^b} = {x^{a + b}}\)
6 مربع یا مجذور یک عدد:
\({x^2}\)
7مکعب یک عدد:
\({x^3}\)
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
جملات متشابه
جملات متشابه
جملاتی که قسمت حروفی و توان آن ها عیناً مثل هم باشند را متشابه گویند.
مثال
در مورد هر قسمت مشخص کنید که جملات متشابه اند.
\((4b\,,\, - 9b)\)(الف
عبارت 4b و -9b با هم متشابه هستند، زیرا قسمت حرفی آن ها یعنی «b» یکسان می باشد.
\(( - \frac{6}{5}{x^2}yz\,,\,3{x^2}yz)\)(ب
عبارت \( - \frac{6}{5}{x^2}yz\) و \(3{x^2}yz\) با هم متشابه هستند زیرا قسمت حرفی آن ها یعنی «\({x^2}yz\) » یکسان می باشد.
از بین جمله های زیر، جمله های متشابه را پیدا کنید و آن ها را مشخص کنید.
\( - 8{x^2}\,,\,\frac{3}{5}xy\,,\,6a{b^2}\,,\,{x^2}\,,\,\frac{3}{4}{b^2}a\,,\,5xy\,,\,4{x^2}\)
1- عبارات \( - 8{x^2}\)و \(4{x^2}\)و \(1{x^2}\)با هم متشابه هستند زیرا قسمت حرفی آن ها یعنی \({x^2}\)یکسان می باشد.
2- عبارات \(\frac{3}{5}xy\) و\(5xy\) باهم متشابه هستند زیرا قسمت حرفی آن ها یعنی\(xy\)یکسان می باشد.
3- عبارات \(6a{b^2}\)و \(\frac{3}{4}a{b^2}\) با هم متشابه هستند زیرا قسمت حرفی آن ها یعنی\(a{b^2}\)یکسان می باشد.
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم فصل 1 عددهای صحیح و گویا
جزوه جامع ریاضی هشتم فصل 2 عددهای اول
جزوه جامع ریاضی هشتم فصل 3 چندضلعی ها
جزوه جامع ریاضی هشتم فصل 4 جبر و معادله
جزوه جامع ریاضی هشتم فصل 5 بردار و مختصات
جزوه جامع ریاضی هشتم فصل 6 مثلث
جزوه جامع ریاضی هشتم فصل 7 توان و جذر
جزوه جامع ریاضی هشتم فصل 8 آمار و احتمال
جزوه جامع ریاضی هشتم فصل 9 دایره
ساده کردن عبارات جبری
ساده کردن عبارت جبری
ابتدا جمله های متشابه را مشخص می کنیم، سپس ضرایب جملات متشابه را جمع یا تفریق کرده و جمله های غیرمتشابه به همان صورت می نویسیم.
مثال
عبارت جبری زیر را ساده کنید.
\(6{m^2} - 5y + 3my + 10{m^2} + 7my = \)(الف
\(\begin{array}{l}6{m^2} - 5y + 3my + 10{m^2} + 7my = \\\\(6 + 10){m^2} - 5y + (3 + 7)my = 16{m^2} - 5y + 10my\end{array}\)
ب)\(3(4x - 5x) + 15{x^2} - 6x = \)
طبق رعایت اولویت ها ابتدا عمل ضرب که مقدم تر بر جمع و تفریق می باشد را انجام می دهیم عدد 3 را در هر یک از یک جمله ای های درون پرانتز ضرب می کنیم و بقیه جمله را می نویسیم سپس بعد از عمل ضرب عبارت جبری را ساده می کنیم و حاصل را به دست می آوریم:
\(\begin{array}{l}3(4x - 5x) + 15{x^2} - 6x = (3 \times 4)x - (3 \times 5)x + 15{x^2} - 6x = \\\\12x - 15x + 15{x^2} - 6x = (12 - 15 - 6)x + 15{x^2} = - 9x + 15{x^2}\end{array}\)
(پ\(2(xy - 4) - (7xy - 8) = \)
یک جمله ای یعنی 2 را در هر یک از جمله های چند جمله ای ضرب می کنیم سپس چند جمله ای که درون پرانتز قرینه می شود. در نتیجه عبارت جبری را ساده می کنیم و حاصل را به دست می آوریم:
\(2(xy - 4) - (7xy - 8) = 2xy - 8 - 7xy + 8 = - 5xy\)
اگر در یک عبارت جبری جمله های متشابه وجود نداشت آن عبارت قابل ساده شدن نیست.
آیا در هر قسمت، جملات مشابه وجود دارند؟
(الف\(4x - 5y\)
با هم متشابه نیستند چون قسمت حرفی آن ها x و y یکسان نمی باشد.
(ب\(2m + 3a - 1\)
با هم متشابه نیستند چون قسمت حرفی آن ها a و m یکسان نمی باشد.
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر
ضرب عبارت های جبری
ضرب دو جمله ای
ضریب های عددی در هم و متغیرها نیز در هم ضرب می شوند؛ مانند:
\(3a(4b) = (3 \times 4)(a \times b) = 12ab\)
ضریب a یعنی عدد 3 را در ضریب b یعنی عدد 4 ضرب و متغیرها را در هم ضرب می کنیم.
در ضرب متغیرها اگر متغیرها مثل هم باشند به صورت توان دار نوشته می شوند در غیر این صورت کنار هم نوشته می شوند. مثلاً:
\( - 4n( + 2n) = ( - 4 \times 2)(n \times n) = - 8{n^2}\)
ضرب یک جمله ای در چندجمله ای
یک جمله ای در هر یک از جمله های چندجمله ای ضرب می شود. به مثال های زیر توجه کنید:
(الف\(2(5x - 3y) = 2(5x) - 2(3y) = 10x - 6y\)
(ب\(\frac{1}{3}(6a - 12b) + 2( - 5a + 10b) = \frac{1}{3}(6a) - \frac{1}{3}(12b) + \)
\(2( - 5a) + 2(10b) = 2a - 4b - 10a + 20b\)
ابتدا عدد پشت پرانتز را در یک جمله ای های داخل پرانتز ضرب می کنیم و اگر جملات مشابه داشته باشیم، سپس ساده می کنیم و حاصل عبارت را به دست می آوریم.
ضرب چندجمله ای در چندجمله ای
هر یک از جمله های چند جمله ای اول را در همه جمله های دوم ضرب می کنیم سپس عبارت را ساده می کنیم؛ مانند:
\(\begin{array}{l}(x + 2)(x + 1) = x(x) + x(1) + 2(x) + 2(1) = \\\\{x^2} + x + 2x + 2 = {x^2} + 3x + 2\end{array}\)
با توجه به اینکه اولویت ضرب نسبت به جمع و تفریق مقدم تر است برای ساده کردن هر عبارت جبری ابتدا ضرب ها را انجام داده سپس جمع و تفریق انجام می دهیم. به عنوان مثال:
\(\begin{array}{l} - 8{x^2}y + 2x(4xy + 5) = - 8{x^2}y + 2x(4xy) + 2x(5) = \\\\ - 8{x^2}y + 8{x^2}y + 10x = 10x\end{array}\)
جمله ی اول یعنی \( - 8{x^2}y\) را می نویسیم سپس ضرب یک جمله ای در چند جمله ای را طبق توضیحات بالا عمل کرده، یک بار 2x را در جمله ی اول درون پرانتز یعنی 4xy و یک بار 2x را در جمله ی دوم درون پرانتز یعنی 5 ضرب می کنیم و عبارت به دست آمده را ساده می کنیم.
مثال
با توجه به شکل و تساوی مساحت ها در دو قسمت یک تساوی جبری بنویسید.
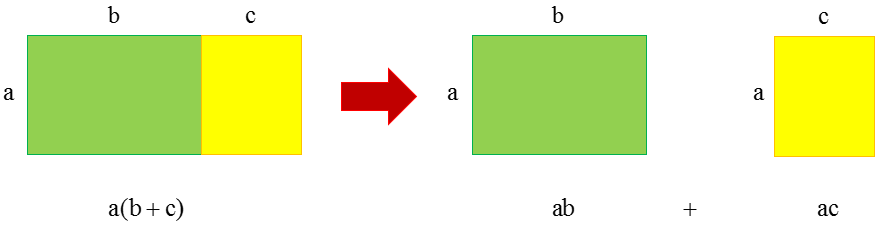
ابتدا یک مستطیل رسم می کنیم و طول آن را به دو قسمت نامساوی تقسیم می کنیم و مساحت آن را به دست می آوریم سپس آن مستطیل را از قسمت طول شکسته و به دو مستطیل با طول های متفاوت ولی عرض های یکسان تقسیم می کنیم سپس مجموع مساحت مستطیل جدید را به دست می آوریم. اگر دو حالت را با هم مقایسه کنیم متوجه می شویم که مساحت هر دو حالت با هم برابر است.
مساحت شکل زیر را با عبارت جبری نشان دهید.
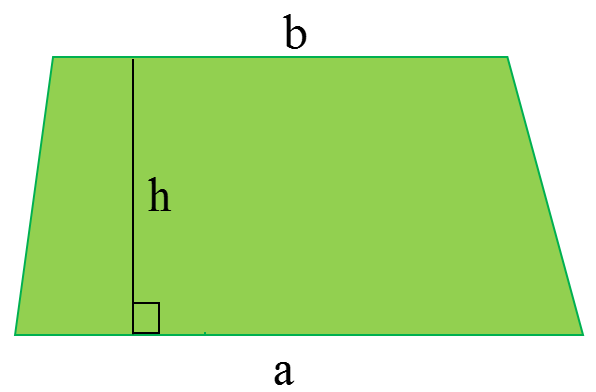
ابتدا مساحت شکل را به صورت فارسی می نویسیم سپس در رابطه به جای کلمات فارسی حروف انگلیسی را قرار می دهیم. در شکل قاعده ها با حروف کوچک a و b و ارتفاع با حرف h نامگذاری شده اند و مساحت را با حرف S نشان می دهیم:

برای به دست آوردن محیط اشکال هندسی مانند تمرین قبل ابتدا محیط شکل موردنظر را به صورت فارسی می نویسیم سپس در رابطه به جای کلمات فارسی حرف انگلیسی را جایگزین می کنیم دقت داشته باشید که محیط را با حرف P نشان می دهیم.
در شکل زیر تعداد چوب کبریت ها در شکل n ام چند تا است؟
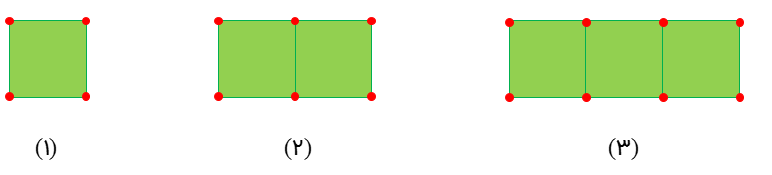
به رابطه های زیر در هر شکل توجه کنید. با کمی دقت متوجه می شوید که شماره های هر شکل در 3 ضرب شده سپس یک واحد به آن اضافه شده است بنابراین شکل n ام دارای 3n+1 چوب کبریت خواهد بود.
جمله ی n ام الگوی جبری زیر را بنویسید.
1 , 4 , 9 , 16 , 25 , …
دقت داشته باشید شماره هر جمله در خودش ضرب شده و در زیر عدد مورد نظر می نویسیم الگوی مورد نظر به دست آوردیم جمله ی n ام که مشخص می شود\(n \times n\)برابر می شود \({n^2}\) .
عدد دو رقمی ab را با نماد \(\overline {ab} \) نمایش می دهیم بنابراین \(\overline {ab} = 10a + b\)
عدد 47 ار می توان به صورت گسترده 40+7 یا 4×10+7 نوشت.
نشان دهید مجموع هر عدد دو رقمی با مقلوب آن همواره مضرب 11 می باشد.
\(\overline {ab} + \overline {ba} = 10a + b + 10b + a = 11a + 11b = 11(a + b)\)
عدد دو رقمی را با توجه به نکته ی بالا \(\overline {ab} \) می نویسیم و با مقلوب آن یعنی \(\overline {ba} \) جمع می کنیم و بعد از جایگذاری به جای هر کدام و ساده کردن عبارت حاصل را به دست می آوریم.
نشان دهید تفاضل هر عدد دو رقمی از مقلوبش مضرب 9 است.
\(\overline {ab} - \overline {ba} = 10a + b - (10b + a) = 9a - 9b = 9(a - b)\)
عدد دو رقمی را با توجه به نکته ی بالا \(\overline {ab} \) می نویسیم و مقلوب آن یعنی \(\overline {ba} \) را از آن کم می کنیم و بعد از جایگذاری به جای هر کدام و ساده کردن عبارت حاصل را به دست می آوریم.
92-29=63=9×7
85-58=27=9×3
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
پیدا کردن مقدار یک عبارت جبری
پیدا کردن مقدار یک عبارت جبری
هرعبارت جبری شامل یک یا چند متغیره اگر به جای این متغیرها عدد قرار دهیم حاصل ان عبارت جبری به دست می اید.
در عبارت جبری متغییر را بر میداریم و به جای ان عددی که گفته شده را با پرانتز می گذاریم (اگر پرانتز قرار ندهیم مشکلی پیش نمی اید اما پیشنهاد می کنم همیشه گذاشتن پرانتز را رعایت کنید)
مثال
مقدارعددی هریک از عبارت های زیر را به ازای مقادیر \(a = 2\)و \(b = 3\) حساب کنید.
الف) \(a + 4 = \)
به جای متغییر a مقداری که در سوال داده شده را قرار می دهیم و با عدد بعدی جمع می کنیم و حاصل را به دست می اوریم.
الف) \(a + 4 = (2) + 4 = 6\)
ب)\(2a + 6b = \)
ابتدا عدد 2 را می نویسیم و به جای متغیرa مقدار مورد نظر در سوال را جایگزین می کنیم سپس عدد6 را می نویسیم و به جای متغیرb مقدار داده شده در سوال را جایگزین می کنیم و حاصل را به دست می اوریم.
ب)\(2a + 6b = 2(2) + 6( - 3) = 4 - 18 = - 14\)
وقتی یک عددی قبل از یک متغیری چسبیده باشد و یا وقتی چند تا متغییر به هم چسبیده باشد یعنی بین انها علامت ضرب وجود دارد طبق نکته بالا جایگزین می کنیم و با رعایت اولویت های انجام محاسبات به محاسبه حاصل عبارت می پردازیم.
مثال
عبارت های جبری زیر را به ازای مقادیر داده شده بدست اورید.
الف)\(5xy - 2y + 3\,({\rm{x}}\,{\rm{ = }}\,{\rm{2}}\,,{\rm{y}}\,{\rm{ = }}\,{\rm{ - 1}})\)
\({\rm{5xy - 2y + 3 = 5(2)( - 1) - 2( - 1) + 3 = - 10 + 2 + 3 = - 5}}\)
در جمله اول و دوم چون عدد به متغیرها چسبیده است، عدد را می نویسیم و به جای متغیرها مقادیر داده شده آن ها را جایگزین می کنیم و بعد عملیات ضرب ، جمع و تفریق را انجام داده و در نتیجه حاصل را به دست می اوریم
ب)\( - 2a + 5{b^2} - 3{a^2}{b^3}{\rm{ (a = - 3 , b = - 1)}}\)
\( - 2a + 5{b^2} - 3{a^2}{b^3}{\rm{ = - 2( - 3) + 5( - 1}}{{\rm{)}}^2} - 3{( - 3)^2}{( - 1)^{ - 3}} = 6 + 5 + 27 = 38\)
در عبارتت داده شده متغیرها توان دار می باشند ابتدا عدد چسبیده به متغیرها را می نویسیم و به جای هر متغیر مقدار داده شده را جایگزین می کنیم و در پرانتز می گذاریم ، سپس هر متغیری که توان دارد، توان ان را بالای پرانتز مقدار جایگزین شده قرار می دهیم و با رعایت اولویت ها به محاسبه حاصل عبارت می پردازیم.
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم فصل 1 عددهای صحیح و گویا
جزوه جامع ریاضی هشتم فصل 2 عددهای اول
جزوه جامع ریاضی هشتم فصل 3 چندضلعی ها
جزوه جامع ریاضی هشتم فصل 4 جبر و معادله
جزوه جامع ریاضی هشتم فصل 5 بردار و مختصات
جزوه جامع ریاضی هشتم فصل 6 مثلث
جزوه جامع ریاضی هشتم فصل 7 توان و جذر
جزوه جامع ریاضی هشتم فصل 8 آمار و احتمال
جزوه جامع ریاضی هشتم فصل 9 دایره
اعداد زوج و فرد
اعداد زوج
از ضرب عدد 2 دریک عدد صحیح ،یک عدد زوج به دست می آید. (اگرk یک عدد صحیح باشد، 2k یک عدد زوج است)
مثال
آیا حاصل جمع دو عدد زوج ،عددی زوج است؟
فرض کنیم a و b دوعدد طبیعی زوج باشد نشان می دهیم:
\(a = 2n{\rm{ }}(n \in N){\rm{ }},{\rm{ }}b = 2m(m \in N) \Rightarrow a + b = 2n + 2m = 2(n + m) = 2k{\rm{ (k}} \in {\rm{n)}}\)
(\(m + n\)را یک عدد طبیعی مانند k فرض می کنیم(
اگر عدد 2 در هر عددی ضرب شود حاصل همواره زوج خواهد بود چون تمام اعداد مضرب 2 هستند.
اعداد فرد
اگر از یک عدد زوج یک واحد کم کنیم یا یک واحد به ان اضافه کنیم عدد فرد به دست می اید.
(اگر h یک عدد صحیح باشد 2h-1 یا 2h-1 یک عدد فرد است)
نشان دهید حاصل ضرب یک عدد زوج در یک عدد فرد عددی زوج است.
فرض می کنیم a عددی طبیعی و زوج و b عددی طبیعی و فرد باشد.
\(a = 2n{\rm{ }},{\rm{ }}b = 2m - 1{\rm{ }},{\rm{ }}(n,m \in N)\)
پس a وb را در هم ضرب میکنیم و مقادیر داده شده را جایگزین می کنیم.
\(a \times b = (2n)(2m - 1) = 2 \times n \times (2m - 1) = 2(2nm - n) = 2c\)
(\(2nm - n\)را یک عدد طبیعی مانند c فرض می کنیم)
حاصل ضرب هر عدد طبیعی در عدد 2، عددی زوج است.
عبارت جبری زیر را به ازای مقادیر داده شده به دست اورید.
\(\frac{{4xy + 3z}}{{ - 2x + 5y}}{\rm{ (x = - 1 , y = 1 , z = 2)}}\)
\(\frac{{4( - 1)(1) + 3(2)}}{{ - 2( - 1) + 5(1)}} = \frac{{ - 4 + 6}}{{ + 2 + 5}} = \frac{2}{7}\)
ابتدا خط کسری را می کشیم و در صورت کسر عدد 4 و3 را با عمل جمع می نویسیم و به جای متغیرها مقادیر داده شده را درون پرانتز جایگزین می کنیم و مخرج کسر را به همین صورت نوشته و محاسبات را انجام داده و حاصل را بدست می اوریم.
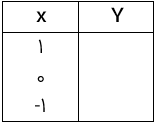
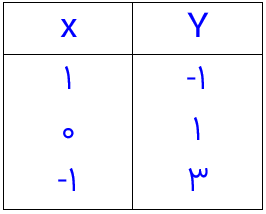
با توجه به رابطه x و y، مقدار y را بدست اورید و جدول را کامل کنید.
\(y = - 2x + 1\)
جای x عدد 1 را در رابطه قرار می دهیم و حاصل به دست امده را در جدول به جای y می گذاریم نقطه های داده شده در x را به همین صورت در رابطه جایگزین می کنیم و مقدار y را به دست می اوریم.
\(\begin{array}{l}y = - 2(1) + 1 = - 2 + 1 = - 1\\\\y = - 2(0) + 1 = 0 + 1 = 0\\\\y = - 2( - 1) + 1 = 2 + 1 = 3\end{array}\)
مثال
چرا مجموع دو عدد فرد عددی زوج می شود؟
\((2k + 1) + (2t + 1) = 2k + 2t + 2 = 2(k + t + 1) \Rightarrow \) مضرب 2است \( \Rightarrow \) زوج است
مثال
مجموع دو عدد که یکی زوج ودیگری فرد باشد ، زوج می شود یا فرد؟چرا؟
\(2m + (2m + 1) = 2n + 2m + 1 = 2(n + m) + 1 \Rightarrow \) عددی فرد است
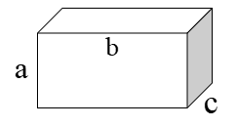
الف) مساحت کل مکعب مستطیل روبرو را به صورت جبری بنوییسید.
ابتدا فرمول شکل را به صورت جبری مینویسیم
\(s = s' + 2s' \Rightarrow s' = p{\rm{ \times c}} \Rightarrow 2(a + b) \times c = 2ac + 2bc\) کل
وقتی مساحت جانبی یعنی(s’) و مساحت مستطیل یعنی(s) را بدست می اوریم \(s = a \times b = ab\) مستطیل را در را در رابطه جایگزین می کنیم.
\(s = 2ac + 2bc + 2ab = 2(ac + bc + ab)\)
عدد2 را در سه جمله فاکتور می گیریم
ب)اگر\(c = 3{\rm{ , }}b = 6{\rm{ }},{\rm{ }}a = 2\) باشند مساحت کل چقدر می شود؟
بعد از به دست امدن مساحت کل مقادیر داده شده را جایگزین می کنیم:
\(s = 2(12 + 6 + 18) = 72\)
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر
تجزیه عبارت های جبری
تجزیه عبارت های جبری
در تجزیه (تبدیل به ضرب یا فاکتور گیری) عبارت های جبری به روش های زیر عمل می کنیم:
گام1: اگر هر دو عبارت عدد داشتن (ب.م.م) آن دو عدد را می نویسیم.
گام 2: حروف انگیلیسی را با کمترین توانی که در جمله دارند می نویسیم.
گام3: تمام جملات را بر جمله مشترک به دست امده تقسیم کرده و حاصل را داخل پرانتز می نویسیم.
مثال
الف)\(7abc + 3ab\)
ابتدا دو عبارت را تجزیه و عامل مشترک را مشخص می کنیم:
\(\left. \begin{array}{l}7abc = 7a \times b \times c\\\\3ab = 3 \times a \times b\end{array} \right\} \Rightarrow 7abc + 3ab = ab(7c + 3)\)
ب)\(9{x^2}{y^3} - 15{x^3}{y^2}\)
\(\left. \begin{array}{l}9{x^2}{y^2} = 3 \times 3 \times x \times x \times y \times y \times y\\\\15{x^2}{y^2} = 3 \times 5 \times x \times x \times x \times y \times y\end{array} \right\} \Rightarrow 9{x^2}{y^2} - 15{x^2}{y^2} = 3{x^2}{y^2}(3y - 5x)\)
پ)\(\frac{{{x^2}y + {x^2}z}}{{{x^2}y - {x^2}z}}\)
علامت صورت و مخرج شبه هم هستند فقط علامت بین آن ها متفاوت می باشد ،پس یکی از دو عبارت را تجزیه کرده و جایگزین می کنیم در صورت ساده شدن کسر مورد نظر را ساده می کنیم و حاصل را به دست می اوریم.
\(\begin{array}{l}\left. \begin{array}{l}{x^2}y = x \times x \times y\\\\{x^2}y = x \times x \times z\end{array} \right\} \Rightarrow {x^2} = (y + z)\\\\\frac{{{x^2}y + {x^2}z}}{{{x^2}y - {x^2}z}} = \frac{{{x^2}(y + z)}}{{{x^2}(y - z)}} = \frac{{(y + z)}}{{(y - z)}}\end{array}\)
اگر عبارت جبری را بخواهیم به توان برسانیم آن را به تعداد توانش ضرب می کنیم.
مثال
\({(x + y)^2} = (x + y)(x + y) = {x^2} = xy + xy + {y^2} = {x^2} + 2xy + {y^2}\)
ابتدا جمله ای را به صورت ضرب دو پرانتز می نویسیم سپس مراحل ضرب چند جمله ای انجام می دهیم و عبارت جبری را ساده می کنیم و حاصل را به دست می آوریم.
به توان رساندن یک عبارت جبری به این معنا نیست که در هر جمله آن را به توان برسانیم.
\({(x + y)^2} \ne {x^2} + {y^2}\)
عامل های مشترک دوجمله جبری را بنویسید.
الف)\(44{a^2}{\rm{ }},{\rm{ }}88{a^2}b\)
ابتدا(ب.م.م) ، \((44,88) = 44\) را بدست می اوریم حرف \(({a^2})\) مشترک است با توان یکسان .در نتیجه عامل مشترک برابر \(44{a^2}\) می باشد.
عبارت های جبری زیر را ساده کنید.
الف)\((2x - 3y) = \)
\(\begin{array}{l}{(2x - 3y)^2} = (2x - 3y)(2x - 3y)\\\\ = (2x \times 2x) + 2x( - 3y) - 3y(2x) - 3y( - 3y) = 4{x^2} - 6xy - 9{y^2}\\\\ = 4{x^2} - 12xy + 9{y^2}\end{array}\)
ب)\({a^2} + {b^2} - {(a - b)^2}\)
ابتدا چند جمله ای را به صورت ضرب دو پرانتز می نویسیم و طبق مراحل گفته شده حاصل را به دست می اوریم.
\((a - b)(a - b) = {a^2} - ab - ab + {b^2} = {a^2} - 2ab + {b^2}\)
سپس حاصل به دست امده را در عبارت جایگزین می کنیم و عبارت درون پرانتز را قرینه می کنیم.
\( = {a^2} + {b^2} - ({a^2} - 2ab + {b^2}) = {a^2} + {b^2} - {a^2} + 2ab - {b^2} = 2ab\)
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
معادله و حل آن
معادله
یک تساوی جبری است که به ازای مقادیر خاصی از مجهول برقرارباشد
حل معادله
برای حل یک معادله باید ابتدا تمام مقدارعددی را به یک تساوی انتقال دهیم و در نهایت با تقسیم کردن مقدار عددی به دست امده بر ضریب مجهول جواب معادله بدست می آید.
وقتی عددی را از یک طرف تساوی به طرف دیگر ان انتقال می دهیم علامت ان را باید تغییر دهیم.
مثال
\(7a - 2 = 19\)
\(7a = 19 + 2 \Rightarrow a = \frac{{21}}{7} = 3 \Rightarrow a = 3\)
ابتدا معادله را مرتب می کنیم معلوم ها یک طرف تساوی و مجهول ها در طرف دیگر تساوی قرار می دهیم .سپس بعد از ساده کردن عدد معلوم را بر ضریب مجهول تقسیم می کنیم و مقدار مجهول را به دست می اوریم.
اگر در معادله پرانتز داشته باشیم با رعایت اولویت ها و با انجام ضرب ،پرانتز را از بین می بریم ان گاه معادله را حل می کنیم
مثال
\(12(m - 2) = 6m\)
\(12m - 24 = 6m \Rightarrow 12m - 6m = 24 \Rightarrow 6m = 24 \Rightarrow m = \frac{{24}}{6} \Rightarrow m = 4\)
عدد پشت پرانتز را در هریک از جمله های درون پرانتز ضرب می کنیم سپس معادله را حل می کنیم.
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم فصل 1 عددهای صحیح و گویا
جزوه جامع ریاضی هشتم فصل 2 عددهای اول
جزوه جامع ریاضی هشتم فصل 3 چندضلعی ها
جزوه جامع ریاضی هشتم فصل 4 جبر و معادله
جزوه جامع ریاضی هشتم فصل 5 بردار و مختصات
جزوه جامع ریاضی هشتم فصل 6 مثلث
جزوه جامع ریاضی هشتم فصل 7 توان و جذر
جزوه جامع ریاضی هشتم فصل 8 آمار و احتمال
جزوه جامع ریاضی هشتم فصل 9 دایره
حل معادلات جبری کسر
حل معادلات جبری کسر
برای حل معادلات جبری کسری به روش زیر عمل می کنیم:
1- حل معادلات کسری به روش طرفین وسطین :
از روش طرفین وسطین زمانی استفاده می کنیم که فقط دو کسر مساوی داشته باشیم در این روش صورت هر کسر در مخرج کسر دیگر ضرب شده و مخرج ها را حذف می کنیم.
مثال
\(\frac{{5x - 3}}{4} = \frac{{2x + 6}}{1}\)
\(\begin{array}{l}1(5x - 3) = 4(2x + 6) \Rightarrow 5x - 3 = 8x + 24 \Rightarrow 5x - 8x = 24 + 3\\\\ \Rightarrow - 3x = 27 \Rightarrow x = \frac{{ - 27}}{3} \Rightarrow x = - 9\end{array}\)
چون عبارت بعد از مساوی مخرج ندارد به آن مخرج 1 می دهیم صورت کسر اولی را باید در1 و صورت کسر دومی را باید در 4 ضرب کنیم.
2- حل معادلات کسری به روش حذف مخرج یا مخرج مشترک:
روش مخرج مشترک گرفتن برای کسرها را بلدیم برای معادلات کسری هم می توانیم همان کار را انجام دهیم اما در معادلات کسری به مخرج کسرها احتیاجی نداریم. به همین دلیل این روش را حذف مخرج می گوییم.
مثال
\(\frac{{x + 2}}{{15}} + \frac{{x + 1}}{{10}} = \frac{{8x + 1}}{{30}}\)
\(\begin{array}{l}\frac{{(x + 2) \times 2}}{{15 \times 2}} + \frac{{(x + 1) \times 3}}{{10 \times 3}} = \frac{{(8x + 1) \times 1}}{{30 \times 1}}{\rm{ , }}\left[ {15,10,30} \right] = 30\\\\2 \times (x + 2) + 3 \times (x + 1) = 8x + 1 \Rightarrow 2x + 4 + 3x + 3 = 8x + 1\\\\2x + 3x - 8x = 1 - 4 - 3 \Rightarrow - 3x = - 6 \Rightarrow x = \frac{{ - 6}}{{ - 3}} \Rightarrow x = 2\end{array}\)
3- حل مسئله به کمک معادله :
ابتدا مجهول را با حروف انگلیسی کوچک در نظر می گیریم آن گاه با توجه به مساله، جمله های فارسی را به عدد و علامت های ریاضی تبدبل می کنیم و با حل معادله جواب را به دست می آوریم.
مثال
از 4 برابر عددی 7 تا کم کردیم حاصل 9 شد ان عدد چیست؟
مورد نظر\(4m = 9 + 7 \Rightarrow 4m = 16 \Rightarrow m = \frac{{16}}{4} \Rightarrow m = 4\)
\(4m = 9 + 7 \Rightarrow 4m = 16 \Rightarrow m = \frac{{16}}{4} \Rightarrow m = 4\)
اعداد متوالی به صورت \((n,n + 1,n + 2, \ldots )\) و اعداد فرد یا زوج متوالی را به صورت \((n,n + 2,n + 4, \ldots )\) نشان دهیم.
مثال
مجموع سه عدد فرد متوالی 57 می باشد عدد کوچکتر چند است؟
\(\begin{array}{l}n + (n + 2) + (n + 4) = 57 \Rightarrow 3n + 6 = 57 \Rightarrow 3n + 57 - 6\\3n = 51 \Rightarrow n = \frac{{51}}{3} \Rightarrow n = 17 \Rightarrow \left\{ {17,19,21} \right\}\end{array}\)
عدد کوچک تر=17
تهیه کنندگان: سیده مریم و سیده سمیه علوی فر



1736019749.png)