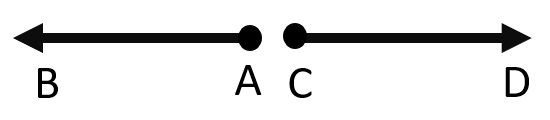درسنامه کامل ریاضی هشتم فصل 5 بردار و مختصات
تعداد بازدید : 7.59Mخلاصه نکات ریاضی هشتم فصل 5 بردار و مختصات - درسنامه شب امتحان ریاضی هشتم فصل 5 بردار و مختصات - جزوه شب امتحان ریاضی هشتم نوبت اول فصل 5 بردار و مختصات
بردارها
بردار
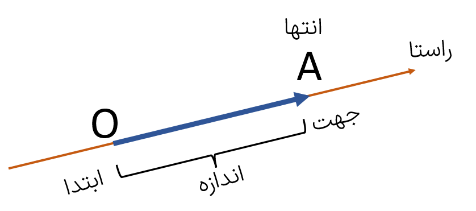
بردار در ریاضی به پاره خط جهت دار بردار می گوییم. بردار \(OA\) را با \(\overrightarrow {OA} \) نشان می دهیم.
بردارهای برابر
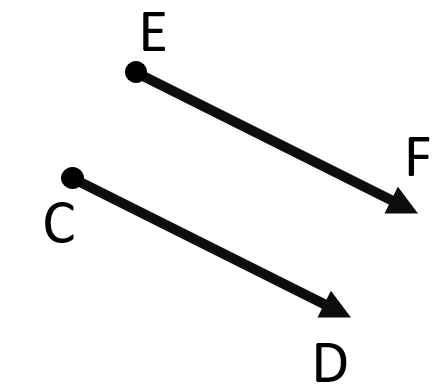
دو بردار وقتی برابرند که هم راستا هم اندازه و هم جهت باشند. مانند بردارهای \(\overrightarrow {CD} \) و \(\overrightarrow {EF} \) :
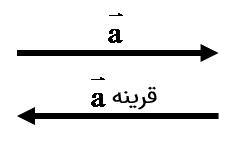
بردارهای قرینه
دو بردار را قرینه می گوییم وقتی هم راستا و هم اندازه باشند. ولی جهت هایشان عکس یکدیگر باشد مانند دو بردار \(\overrightarrow {AB} \) و \(\overrightarrow {CD} \) در شکل روبرو:
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
جمع بردارها
جمع بردارها
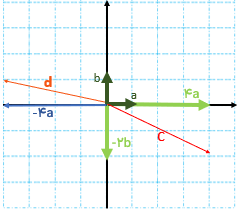
در شکل زیر ابتدا از نقطه ی 1 بردار انتقال a به نقطه ی B می رویم. یعنی ۲ واحد به سمت چپ (افقی) و ۴ واحد به سمت بالا عمودی حرکت می کنیم .
پس بردار انتقال\(\overrightarrow a \)برابر است با \(\overrightarrow a = \left[ \begin{array}{l} - 2\\4\end{array} \right]\) سپس با بردار انتقال \(\overrightarrow b \)از نقطه ی B به نقطه ی C می رویم: \(\overrightarrow b = \left[ \begin{array}{l} - 3\\ - 2\end{array} \right]\)
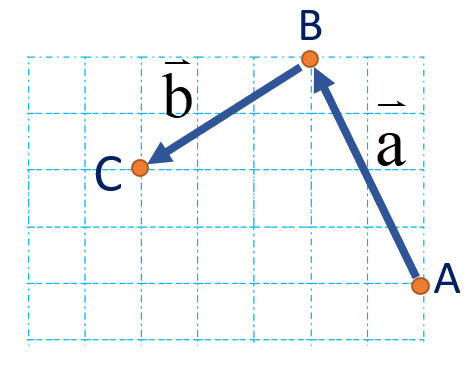
نقطه ی A با بردار \(\overrightarrow {AC} \) به طور مستقیم به نقطه ی C منتقل شده است. نام آن را بردار انتقال \(\overrightarrow C \) می گذاریم.
می توان گفت \(\overrightarrow C \) کار دو بردار انتقال \(\overrightarrow a \)و \(\overrightarrow b \) را انجام می دهد. به بردار \(\overrightarrow C \) بردار برآیند یا حاصل جمع می گویند.
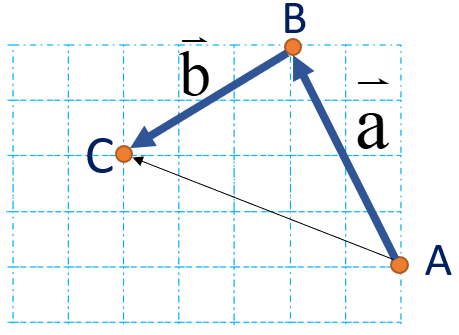
اگر بردار های a و b را با هم جمع کنیم، داریم:
\(\overrightarrow a + \overrightarrow b = \left[ \begin{array}{l} - 2\\ + 4\end{array} \right] + \left[ \begin{array}{l} - 3\\ - 2\end{array} \right] = \left[ \begin{array}{l} - 5\\ + 2\end{array} \right]\)
که حاصل آن طبق شکل بالا برابر \(\overrightarrow {AC} = \overrightarrow c = \left[ \begin{array}{l} - 5\\ + 2\end{array} \right]\) است. بنابراین میتوان یک تساوی برداری به صورت \(\overrightarrow a + \overrightarrow b = \overrightarrow c \) نوشت که تساوی مختصاتی آن هم در بالا نوشته شد.
برای مثال:
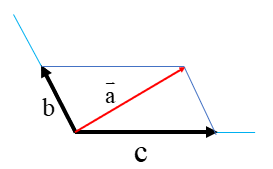
در شکل روبرو بردار\(\overrightarrow a \)حاصل جمع دو بردار\(\overrightarrow b \)و \(\overrightarrow c \) است.
جمع برداری :\(\overrightarrow a + \overrightarrow b = \overrightarrow c \)
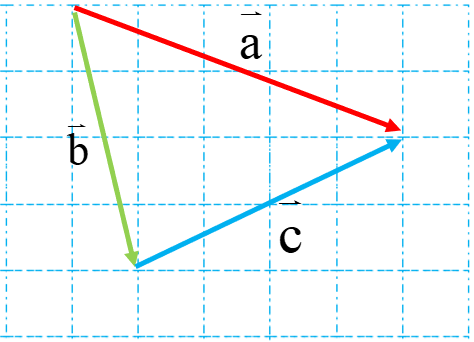
و اگر مختصات آنها را از روی شکل بنویسیم داریم:
جمع مختصاتی: \(\left[ \begin{array}{l} + 1\\ - 4\end{array} \right] + \left[ \begin{array}{l} + 4\\ + 2\end{array} \right] = \left[ \begin{array}{l} + 5\\ - 2\end{array} \right]\)
مثال
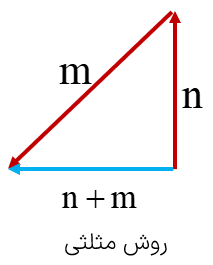
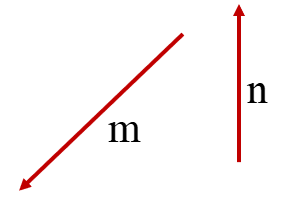
برای شکل زیر یک جمع برداری بنویسید.
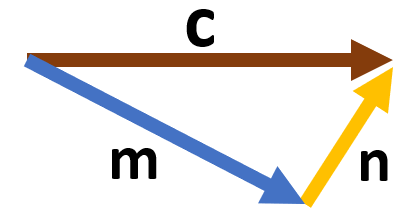
همان طور که می بینیم بردارهای\(\overrightarrow m \) و\(\overrightarrow n \) دنبال هم رسم شده اند. یعنی بردار\(\overrightarrow n \) از انتهای بردار \(\overrightarrow m \) رسم شده است و بردار \(\overrightarrow c \) از اتصال ابتدای \(\overrightarrow n \)به انتهای \(\overrightarrow m \) بدست آمده است پس داریم :\(\overrightarrow m + \overrightarrow n = \overrightarrow c \)
بردارهای مساوی را می توان از نقطه های شروع مختلف رسم کرد.
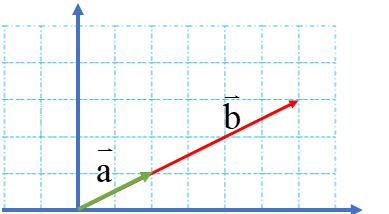
برای مثال می خواهیم دو بردار مساوی بردار\(\overrightarrow a \) در شکل روبرو رسم کنیم.
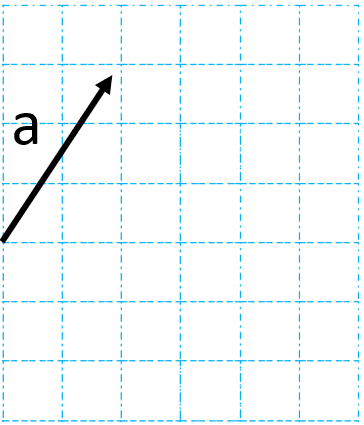
مختصات\(\overrightarrow a \) به صورت \(\overrightarrow a = \left[ \begin{array}{l}2\\3\end{array} \right]\) است. پس مختصات بردارهای رسم شده هم باید همین باشد. می توان بردارهای دیگری نیز مساوی بردار \(\overrightarrow a \)رسم کرد.
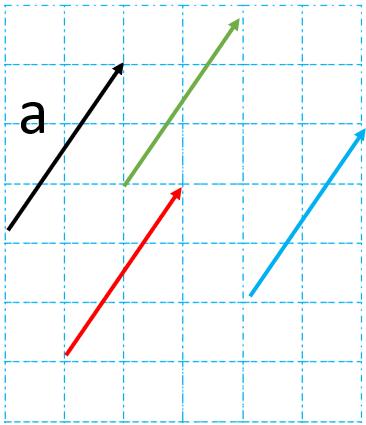
حال با استفاده از نکته بالا می خواهیم حاصل جمع بردارهای\(\overrightarrow a \)و\(\overrightarrow b \)را رسم کنیم:
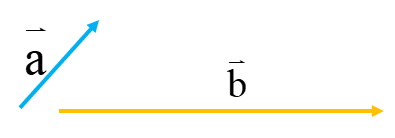
ابتدا دو بردار را دنبال هم رسم می کنیم سپس انتهای\(\overrightarrow a \) را به ابتدای\(\overrightarrow b \) وصل می کنیم بردار حاصل جمع به دست می آید. آن را \(\overrightarrow c \)می نامیم:
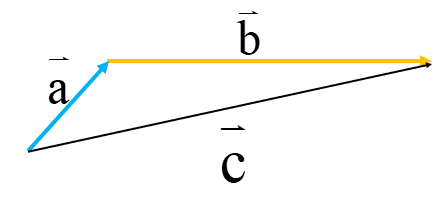
پس: \(\overrightarrow a + \overrightarrow b = \overrightarrow c \)
جمع بردارها خاصیت جابجایی دارد: یعنی اگر در شکل بالا ابتدا \(\overrightarrow b \)را رسم کنیم و سپس\(\overrightarrow a \)را رسم کنیم باز هم بردار حاصل جمع بردار\(\overrightarrow c \)خواهد بود:
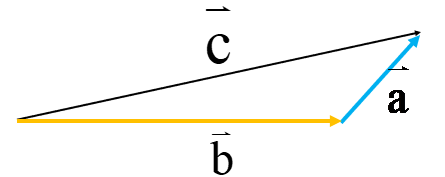
\(\overrightarrow b + \overrightarrow a = \overrightarrow c \)
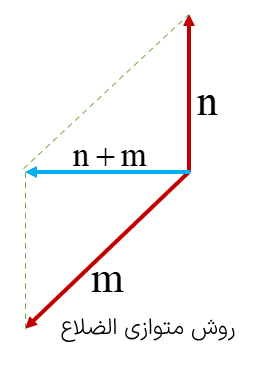
روشی که در بالا برای رسم بردار حاصل جمع گفته شد روش مثلثی نام دارد. روش دیگر برای رسم حاصل جمع دو بردار روش متوازی الاضلاع نام دارد؛ به این صورت که دو بردار را از یک نقطه ی دلخواه به صورت اضلاع مجاور یک متوازی الاضلاع رسم می کنیم، متوازی الاضلاع را تشکیل می دهیم (می دانیم که ضلع های روبروی متوازی الاضلاع با هم برابرند( و قطر متوازی الاضلاع بردار حاصل جمع خواهد بود:

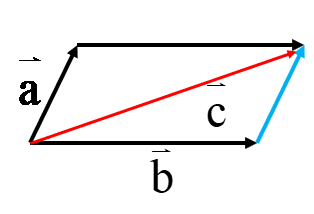
\(\overrightarrow a + \overrightarrow b = \overrightarrow c \)
برای بدست آوردن حاصل جمع سه بردار، ابتدا حاصل جمع دو بردار را به دست می آوریم و سپس بردار حاصل جمع را با بردار سوم جمع می کنیم
مثال
حاصل جمع بردارهای\(\overrightarrow a \)و\(\overrightarrow b \)و\(\overrightarrow c \) را بدست آورید.
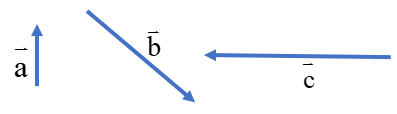
ابتدا بردار \(\overrightarrow a + \overrightarrow b \) را بدست می آوریم ،سپس آن را با\(\overrightarrow c \) جمع می کنیم:
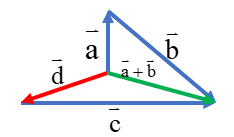
\(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow a = \overrightarrow d \)
گفتیم که در جمع ترتیب بردارها اهمیتی ندارد، پس می توان ابتدا \(\overrightarrow b + \overrightarrow c \) را بدست آورد. سپس آن را با\(\overrightarrow a \)جمع کرد:
\(\left( {\overrightarrow b + \overrightarrow c } \right) + \overrightarrow a = \overrightarrow d \)
همان طور که میبینید باز هم بردار حاصل جمع\(\overrightarrow d \)بدست می آید.
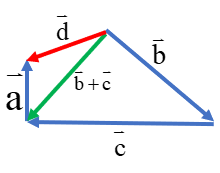
راه حل سوم و البته آسان تر آن است که سه بردار را دنبال هم رسم کنیم (مانند شکل زیر) و سپس ابتدای اولی را به انتهای آخری وصل کنیم:
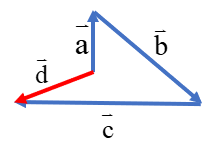
\(\overrightarrow a + \overrightarrow b + \overrightarrow c = \overrightarrow d \)
مثال
حاصل جمع بردارهای زیر را رسم کنید.
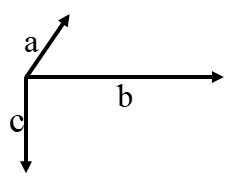
از دو روش قابل حل است:
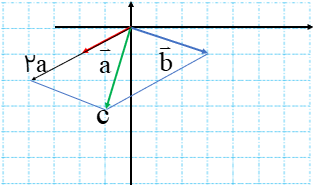
الف) بردار قرمز حاصل جمع بردارهای\(\overrightarrow a \)و\(\overrightarrow b \)است و بردار بنفش بردار\(\overrightarrow a + \overrightarrow b + \overrightarrow c \) است. (روش متوازی الاضلاع)
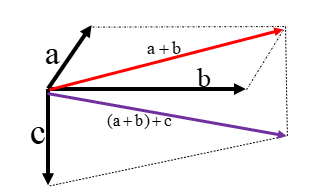
ب) همان طور که می بینید برای بدست آوردن بردار حاصل جمع،کافی است ابتدای بردار اول را به انتهای بردار آخر وصل کنیم.
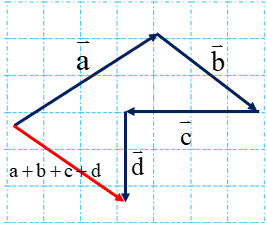
ج) در این قسمت برای تمرین بیشتر از هر دو روش استفاده کردیم.
جمع بردارهای قرینه برابر بردار صفر است. آن را با\(\overrightarrow o \) نشان میدهیم و مختصات آن به صورت\(\left[ \begin{array}{l}0\\0\end{array} \right]\) است.
قرینه ی \(\overrightarrow a \)را با \( - \overrightarrow a \) نشان می دهیم:
\(\overrightarrow a + ( - \overrightarrow a ) = \overrightarrow o \)
مثال
حاصل جمع بردارهای a و b و c چیست؟ چرا؟
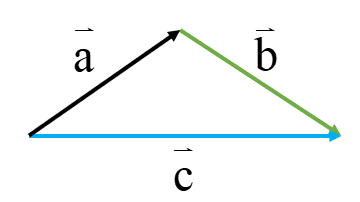
همان طور که می بینید ابتدای بردار a و انتهای بردار C بر یکدیگر منطبق هستند پس حاصل جمع بردارهای a و b و c برابر بردار صفر است.
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم فصل 1 عددهای صحیح و گویا
جزوه جامع ریاضی هشتم فصل 2 عددهای اول
جزوه جامع ریاضی هشتم فصل 3 چندضلعی ها
جزوه جامع ریاضی هشتم فصل 4 جبر و معادله
جزوه جامع ریاضی هشتم فصل 5 بردار و مختصات
جزوه جامع ریاضی هشتم فصل 6 مثلث
جزوه جامع ریاضی هشتم فصل 7 توان و جذر
جزوه جامع ریاضی هشتم فصل 8 آمار و احتمال
جزوه جامع ریاضی هشتم فصل 9 دایره
تجزیه ی بردار
تجزیه ی بردار
تجزیه ی یک بردار در راستاهای داده شده یعنی دو بردار به دست بیاوریم که حاصل جمع آنها بردار داده شده باشد.
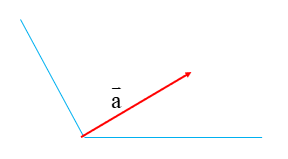
در شکل زیر بردار a در راستاهای آبی رنگ تجزیه شده است. همان طور که می بینید تصویر بردار\(\overrightarrow a \)را بر راستاهای داده شده رسم کرده ایم. می توان بردار \(\overrightarrow a \)را به صورت حاصل جمع و نوشت: \(\overrightarrow a = \overrightarrow b + \overrightarrow c \)
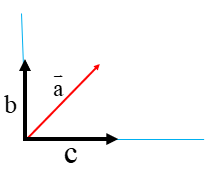
مثال
بردار\(\overrightarrow a \)را در راستاهای داده شده تجزیه کنید بردارهای \(\overrightarrow b \)و\(\overrightarrow c \) را با استفاده از روش متوازی الضلاع طوری رسم می کنیم که \(\overrightarrow b + \overrightarrow c \) برابر بردار \(\overrightarrow a \)شود.
مثال
مختصات دو بردار را که حاصل جمعشان بردار\(\left[ \begin{array}{l}3\\4\end{array} \right]\) باشد، بنویسید.
این سوال جواب های متفاوتی دارد. در اینجا دو تا از آنها را می نویسیم:
\(\begin{array}{l}\left[ \begin{array}{l}1\\2\end{array} \right] + \left[ \begin{array}{l}2\\2\end{array} \right] = \left[ \begin{array}{l}3\\4\end{array} \right]\\\\\left[ \begin{array}{l}3\\1\end{array} \right] + \left[ \begin{array}{l}0\\3\end{array} \right] = \left[ \begin{array}{l}3\\4\end{array} \right]\end{array}\)
در تساوی روبرو x و y را بدست آورید.
\(\left[ \begin{array}{l}3\\ - 4\end{array} \right] + \left[ \begin{array}{l}x\\ - 2\end{array} \right] = \left[ \begin{array}{l}7\\y\end{array} \right]\)
باید جمع طول های دو بردار برابر ۷ و مجموع عرض های آنها برابر شود. بنابراین:
\(\left\{ \begin{array}{l}3 + x = 7\\\\ - 4 + ( - 2) = y\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 7 - 3 = 4\\\\y = - 4 + ( - 2) = 6\end{array} \right.\)
ضرب عدد در بردار
ضرب عدد در بردار
بردارهای a و b در شکل زیر را در نظر بگیرید:
این دو بردار هم جهت هستند اما اندازه ی بردار b سه برابر اندازه ی بردار a است.مختصات آنها را می نویسیم و با هم مقایسه می کنیم:
\(a = \left[ \begin{array}{l}2\\1\end{array} \right]{\rm{ b = }}\left[ \begin{array}{l}6\\3\end{array} \right]\)
همان طور که می بینید طول و عرض در ۳ ضرب شده اند:
\(3 \times \left[ \begin{array}{l}2\\1\end{array} \right] = \left[ \begin{array}{l}6\\3\end{array} \right]{\rm{ }}3 \times \overrightarrow a = \overrightarrow b \)
اکنون دو بردار زیر را در نظر بگیرید:
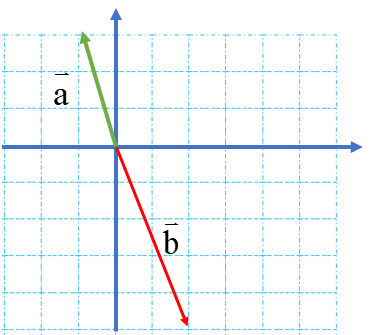
همانطور که می بینید این دو بردار هم جهت نیستند در واقع دو جهت مخالف دارند. حال مختصات آنها را می نویسیم:
\(\begin{array}{l}a = \left[ \begin{array}{l}1\\ + 3\end{array} \right]{\rm{ b = }}\left[ \begin{array}{l} + 2\\ - 6\end{array} \right]\\\\( - 2) \times \left[ \begin{array}{l} - 1\\3\end{array} \right] = \left[ \begin{array}{l} + 2\\ - 6\end{array} \right] \Rightarrow ( - 2) \times \overrightarrow a = \overrightarrow b \end{array}\)
این دو بردار هم راستا هستند ولی هم جهت نیستند.پس برای بدست آوردن حاصل ضرب یک عدد در یک بردار آن عدد را در طول و عرض آن بردار ضرب می کنیم:
\(k{\rm{ \times }}\left[ \begin{array}{l}x\\y\end{array} \right] = \left[ \begin{array}{l}kx\\ky\end{array} \right]\)
نتیجه
1 اگر عدد مثبتی را در یک بردار ضرب کنیم بردار حاصل هم راستا و هم جهت بردار اولی است.
2 گر یک عدد منفی در بردار ضرب ،شود بردار ،حاصل هم راستا ولی در خلاف جهت بردار اولی است.
اگر بردار b قرینه ی بردار a باشد: (شکل روبرو)
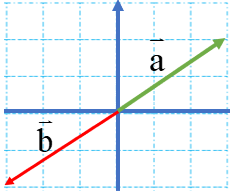
می نویسیم:
\(\begin{array}{l}\overrightarrow b = - \overrightarrow a {\rm{ , }}\overrightarrow b = {\rm{(}} - 1{\rm{)}} \times \overrightarrow a \\\\\overrightarrow a = \left[ \begin{array}{l}x\\y\end{array} \right] \Rightarrow \overrightarrow b = - \overrightarrow a = \left[ \begin{array}{l} - x\\ - y\end{array} \right]\end{array}\)
مثال
با توجه به بردارهای داده شده بردار مورد نظر را رسم کنید.
\(\begin{array}{l}\overrightarrow b = 3\overrightarrow a {\rm{ }}\\\\\overrightarrow y = - 2\overrightarrow x {\rm{ }}\\{\rm{ }}\\\overrightarrow b = \frac{1}{2}\overrightarrow a {\rm{ }}\\{\rm{ }}\\\overrightarrow y = - \frac{3}{2}\overrightarrow x \end{array}\)
\(\begin{array}{l}\overrightarrow b = 3\overrightarrow a {\rm{ }}\\\\\overrightarrow y = - 2\overrightarrow x {\rm{ }}\\{\rm{ }}\\\overrightarrow b = \frac{1}{2}\overrightarrow a {\rm{ }}\\{\rm{ }}\\\overrightarrow y = - \frac{3}{2}\overrightarrow x \end{array}\)
در هر مورد می توانیم مختصات هر بردار و بردار حاصل ضرب را نیز بدست آوریم:
برای مثال:
\(\overrightarrow x = \left[ \begin{array}{l} - 2\\ - 2\end{array} \right] \Rightarrow \overrightarrow y = - \frac{3}{2} \times \left[ \begin{array}{l} - 2\\ - 2\end{array} \right] = \left[ \begin{array}{l}3\\3\end{array} \right]\)
هم چنین برای بردار a می توانیم بنویسیم:
\(\overrightarrow a = \left[ \begin{array}{l} - 2\\0\end{array} \right] \Rightarrow \overrightarrow b = \frac{1}{2} \times \left[ \begin{array}{l} - 2\\0\end{array} \right] = \left[ \begin{array}{l} - 1\\0\end{array} \right]\)
مثال
بردارهای a و b مفروض هستند.
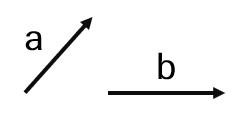
الف) بردار\(\overrightarrow c = 2\overrightarrow a + 3\overrightarrow b \) را رسم کنید.
ابتدا بردارهای a و b را از نقطه ی دلخواه O رسم می کنیم؛ سپس بردارهای\(\overrightarrow a + 3\overrightarrow b \) و\(3\overrightarrow a \) را رسم می کنیم و سپس بردار حاصل جمع C را پیدا می کنیم.
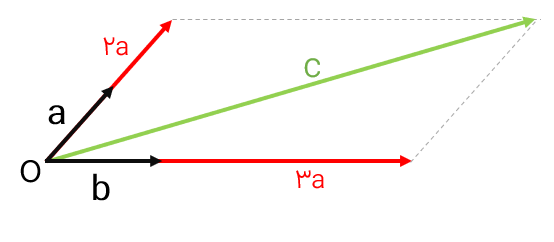
ب) بردار \(\overrightarrow d = \overrightarrow a - \overrightarrow b \) را رسم کنید.
باید بردارهای \(\overrightarrow a \) و\( - \overrightarrow b \) را با هم جمع کنیم. ابتدا بردارهای\(\overrightarrow a \)و\( - \overrightarrow b \) را از یک نقطه رسم می کنیم (روش متوازی الاضلاع)
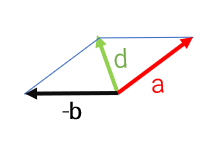
یا دنبال هم رسم می کنیم (روش مثلثی) و همانطور که می بینید بردار حاصل جمع در هر دو شکل یکسان است.
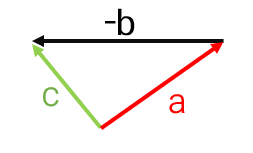
با توجه به بردارهای روبرو، بردار c را رسم کنید.
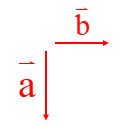
\(\overrightarrow c = 2\overrightarrow a - 3\overrightarrow b = 2\overrightarrow a + ( - 3\overrightarrow b )\)
ابتدا بردارهای \( - 3\overrightarrow b {\rm{ }},{\rm{ }}2\overrightarrow a \) را از یک نقطه رسم می کنیم سپس به روش متوازی الاضلاع بردار حاصل جمع را رسم می کنیم.
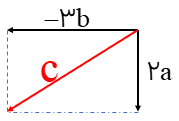
در هر شکل بردار c را بر حسب بردارهای a و b بنویسید.
الف)
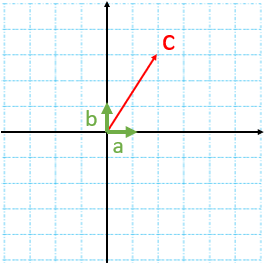
ب)
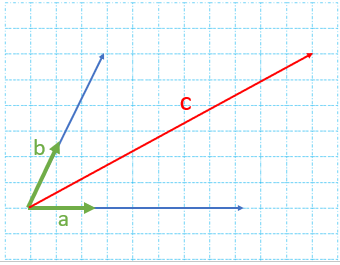
الف) بر حسب نوشتن یعنی بردار c را به صورت حاصل جمع مضرب هایی از بردارهای a و b بنویسیم. اگر متوازی الاضلاعی تشکیل دهیم که بردار c قطر آن باشد. مانند شکل روبرو : (در شکل روبرو طول بردارهای a و b هر کدام یک واحد است)
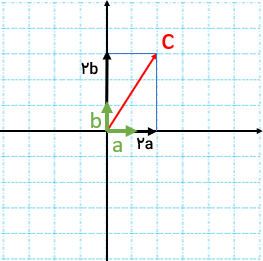
بردار c برابر می شود با \(\overrightarrow c = 2\overrightarrow a + 3\overrightarrow b \)
ب) در این مثال میتوانیم طول بردارهای a و b را با خط کش اندازه بگیریم.
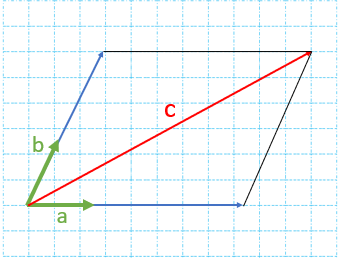
\(\overrightarrow c = 4\overrightarrow a + 2\overrightarrow b \)
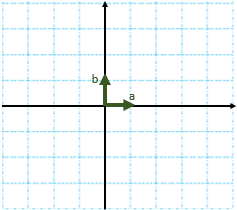
با توجه به بردارهای a و b بردارهای c و d را رسم کنید.
\(\begin{array}{l}\overrightarrow c = 4\overrightarrow a - 2\overrightarrow b \\\\\overrightarrow d = ( - 4\overrightarrow a ) + \overrightarrow b \end{array}\)
حاصل عبارت روبرو را بدست آورید.
\( - 4\left[ \begin{array}{l} - 5\\7\end{array} \right] - \left[ \begin{array}{l}2\\ - 1\end{array} \right] = \)
\( - 4\left[ \begin{array}{l} - 5\\7\end{array} \right] - \left[ \begin{array}{l}2\\ - 1\end{array} \right] = \left[ \begin{array}{l} - 4 \times ( - 5)\\ - 4 \times 7\end{array} \right] - \left[ \begin{array}{l}2\\ - 1\end{array} \right] = \left[ \begin{array}{l}20 - 2\\ - 1\end{array} \right] = \left[ \begin{array}{l}18\\ - 27\end{array} \right]\)
معادله های مختصات زیر را حل کنید (توجه کنید که در اینجا یک بردار است.)
الف) \(\left[ \begin{array}{l}2\\5\end{array} \right] + x = \left[ \begin{array}{l} - 4\\6\end{array} \right] \Rightarrow \)
ب)\( - 3x = \left[ \begin{array}{l}15\\ - 9\end{array} \right] \Rightarrow \)
الف)\(\left[ \begin{array}{l}2\\5\end{array} \right] + x = \left[ \begin{array}{l} - 4\\6\end{array} \right] \Rightarrow x = \left[ \begin{array}{l} - 4\\6\end{array} \right] - \left[ \begin{array}{l}2\\5\end{array} \right] = \left[ \begin{array}{l} - 4 - 2\\6 - 5\end{array} \right] = \left[ \begin{array}{l} - 6\\1\end{array} \right]\)
ب)\( - 3x = \left[ \begin{array}{l}15\\ - 9\end{array} \right] \Rightarrow x = \left[ \begin{array}{l}\frac{{15}}{{ - 3}}\\\frac{{ - 9}}{{ - 3}}\end{array} \right] = \left[ \begin{array}{l} - 5\\3\end{array} \right]\)
با توجه به بردارهای a و b مختصات بردار c را بدست آورید.
\(\overrightarrow a = \left[ \begin{array}{l}2\\1\end{array} \right],\overrightarrow b = \left[ \begin{array}{l} - 2\\3\end{array} \right]{\rm{ }} \to {\rm{ }}\overrightarrow c = \overrightarrow a - 2\overrightarrow b \)
مختصات بردارهای a و b را در معادله ی بالا جایگزین می کنیم
\(\overrightarrow c = \overrightarrow a - 2\overrightarrow b = \left[ \begin{array}{l}2\\1\end{array} \right] - 2\left[ \begin{array}{l} - 2\\3\end{array} \right] = \left[ \begin{array}{l}2 + 4\\1 - 6\end{array} \right] = \left[ \begin{array}{l}6\\ - 5\end{array} \right]\)
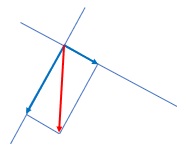
بردار داده شده را روی امتدادهای رسم شده تجزیه کنید.
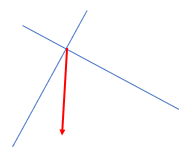
به روش متوازی الاضلاع عمل می کنیم :
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
بردارهای واحد مختصات
بردارهای واحد مختصات
همان طور که می دانیم برای اندازه گیری هر کمیتی از یک واحد استفاده می کنیم. مثلا واحد اندازه گیری زمان ساعت یا دقیقه یا ثانیه است و واحد اندازه گیری زاویه درجه است برای اندازه گیری بردار نیز به واحد نیاز داریم این واحد باید از جنس بردار باشد با توجه به اینکه بردار در صفحه ی مختصات با دو محور نمایش داده می شود به واحدی روی هر دو محور نیاز داریم:
بردار \(\overrightarrow i \) بردار واحد طول و بردار\(\overrightarrow j \)بردار واحد عرض نام دارد.مختصات آنها به صورت زیر است.
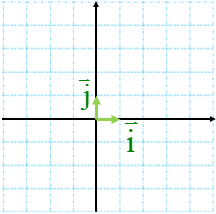
\(\overrightarrow i = \left[ \begin{array}{l}1\\0\end{array} \right],\overrightarrow j = \left[ \begin{array}{l}0\\1\end{array} \right]\)
هر بردار را می توانیم به صورت حاصل جمع مضرب هایی از دو بردار\(\overrightarrow i \)و \(\overrightarrow j \)بنویسیم.
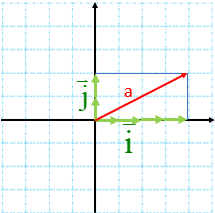
مثلا در شکل زیر بردار\(\overrightarrow a \)برابر است با : \(\overrightarrow a = 4\overrightarrow i + 2\overrightarrow j \)
همچنین می توانیم مختصات بردار\(\overrightarrow c \)را با استفاده از بردارها \(\overrightarrow i \)
و
\(\overrightarrow j \)واحد بدست آوریم.
مثال
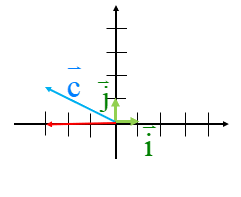
بردار\(\overrightarrow c \) را بر حسب بردارهای\(\overrightarrow i \) و \(\overrightarrow j \)و سپس به صورت مختصاتی بنویسید.
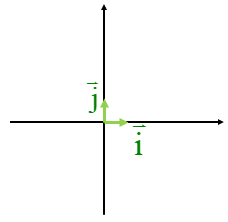
با توجه به شکل می توانیم بنویسیم:\(\overrightarrow c = - 3\overrightarrow i + \overrightarrow j \)
و مختصات آن:
\(\overrightarrow c = - 3\left[ \begin{array}{l}1\\0\end{array} \right] + \left[ \begin{array}{l}0\\1\end{array} \right] = \left[ \begin{array}{l} - 3 + 0\\0 + 1\end{array} \right] = \left[ \begin{array}{l} - 3\\1\end{array} \right]\)
مثال
بردار زیر را بر حسب\(\overrightarrow i \) و\(\overrightarrow j \) بنویسید.
\(\left[ \begin{array}{l}3\\4\end{array} \right]\)
\(\left[ \begin{array}{l}3\\4\end{array} \right] = 3\left[ \begin{array}{l}1\\0\end{array} \right] + 4\left[ \begin{array}{l}0\\1\end{array} \right] = 3\overrightarrow i + 4\overrightarrow j \)
از این پس می توانیم به صورت مختصر بنویسیم:
\(\left[ \begin{array}{l}2\\ - 5\end{array} \right] = 2\overrightarrow i - 5\overrightarrow j {\rm{ , }}\left[ \begin{array}{l}0\\ - 6\end{array} \right] = \overrightarrow i - 6\overrightarrow j = - 6\overrightarrow j {\rm{ , }}\left[ \begin{array}{l}2\\0\end{array} \right] = 2\overrightarrow i + 0\overrightarrow j = 2\overrightarrow i \)
طرف دوم تساوی های زیر را بنویسید.
\(\begin{array}{l}\overrightarrow i + \overrightarrow j = {\rm{ }}\\2\overrightarrow i - \overrightarrow j = {\rm{ }}\\3\overrightarrow j = \end{array}\)
\(\begin{array}{l}\overrightarrow i + \overrightarrow j = \left[ \begin{array}{l}1\\1\end{array} \right]{\rm{ }}\\2\overrightarrow i - \overrightarrow j = \left[ \begin{array}{l}2\\ - 1\end{array} \right]{\rm{ }}\\3\overrightarrow j = \left[ \begin{array}{l}0\\3\end{array} \right]\end{array}\)
معادله ی برداری زیر را حل کنید.
\(2\overrightarrow i - \overrightarrow j + 3\overrightarrow x = \)
برای حل معادله های برداری می توانیم از دو روش استفاده کنیم:
۱- روش بردارهای واحد\(\overrightarrow j ,\overrightarrow i \)
۲- روش مختصاتی
۱- روش بردارهای واحد:
در این روش مانند حل معادله علامت جملات پس از انتقال به طرف دیگر معادله تغییر می کند و جملات مشابه با هم جمع می شوند.
\(\begin{array}{l}2\overrightarrow i - \overrightarrow j + 3\overrightarrow x = - 6\overrightarrow i + 3\overrightarrow j \\\\3\overrightarrow x = - 6\overrightarrow i + 3\overrightarrow j - 2\overrightarrow i + \overrightarrow j \\\\3\overrightarrow x = ( - 6 - 2)\overrightarrow i + (3 + 2)\overrightarrow j \\\\3\overrightarrow x = - 8\overrightarrow i + 4\overrightarrow j \\\\\overrightarrow x = \frac{{ - 8}}{3}\overrightarrow i + \frac{4}{3}\overrightarrow j \end{array}\)
۲- روش مختصاتی
در این روش مختصات بردارها را می نویسیم.
\(\begin{array}{l}2\overrightarrow i - \overrightarrow j + 3\overrightarrow x = \left[ \begin{array}{l} - 6\\3\end{array} \right]\\\\\left[ \begin{array}{l}2\\ - 1\end{array} \right] + 3\overrightarrow x = \left[ \begin{array}{l} - 6\\3\end{array} \right]\\\\3\overrightarrow x = \left[ \begin{array}{l} - 6\\3\end{array} \right] - \left[ \begin{array}{l}2\\ - 1\end{array} \right] = \left[ \begin{array}{l} - 6 - 2\\3 - ( - 1)\end{array} \right]\\\\3\overrightarrow x = \left[ \begin{array}{l} - 8\\4\end{array} \right] \Rightarrow \overrightarrow x = \left[ \begin{array}{l}\frac{{ - 8}}{3}\\\frac{4}{3}\end{array} \right]\end{array}\)
مثال
اگر \(\overrightarrow a = 3\overrightarrow i - 2\overrightarrow j \) و \(\overrightarrow b = 2\overrightarrow i + \overrightarrow j \) مختصات بردارهای x و y را بدست آورید.
\(\begin{array}{l}\overrightarrow x = 5\overrightarrow a + 3\overrightarrow b {\rm{ }}\\\\\overrightarrow y = \overrightarrow a - 2\overrightarrow b \end{array}\)
بردارهای a و b را در معادله ی داده شده جایگزین می کنیم.
\(\begin{array}{l}\overrightarrow x = 5\overrightarrow a + 3\overrightarrow b = 5(3\overrightarrow i + \overrightarrow j ) + 3(2\overrightarrow i + \overrightarrow j ) = \\\\ \Rightarrow 15\overrightarrow i - 10\overrightarrow j + 6\overrightarrow i + 3\overrightarrow j = (15 + 6)\overrightarrow i + ( - 10 + 3)\overrightarrow j = 21\overrightarrow i - 7\overrightarrow j \\\\\overrightarrow y = \overrightarrow a - 2\overrightarrow b = 3\overrightarrow i - 2\overrightarrow j - 2(2\overrightarrow i + \overrightarrow j ) = \\\\ \Rightarrow 3\overrightarrow i - 2\overrightarrow j - 4\overrightarrow i - 2\overrightarrow j = - \overrightarrow i - 4\overrightarrow j \end{array}\)
بردار \(\overrightarrow b = \left[ \begin{array}{l} - 2\\3\end{array} \right]\) را در دستگاه مختصات و رسم کنید، و آن را بر حسب بردارهای واحد و بنویسید.
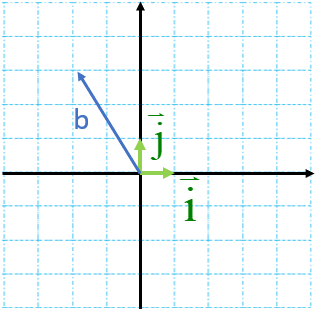
\(\overrightarrow b = - 2\overrightarrow i + 3\overrightarrow j \)
با توجه به شکل زیر مختصات بردار c را با دو روش زیر پیدا کنید.
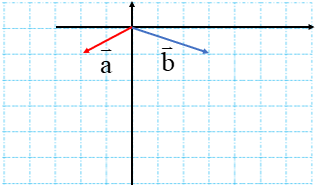
\(\overrightarrow c = 2\overrightarrow a + \overrightarrow b \)
الف) رسم شکل و نوشتن مختصات بردار c از روی شکل:
ابتدا بردار 2a را رسم می کنیم و سپس آن را با بردار bجمع می کنیم با توجه به شکل روبرو مختصات بدست می آید:
\(\overrightarrow c = \left[ \begin{array}{l} - 1\\ - 3\end{array} \right]\)
ب) پیدا کردن مختصات a و b و قرار دادن آنها در معادله ی :
\(\overrightarrow c = 2\overrightarrow a + \overrightarrow b = 2\left[ \begin{array}{l} - 2\\ - 1\end{array} \right] + \left[ \begin{array}{l}3\\ - 1\end{array} \right] = \left[ \begin{array}{l} - 4 + 3\\ - 2 - 1\end{array} \right] = \left[ \begin{array}{l} - 1\\ - 3\end{array} \right]\)
روش الف هندسی و با استفاده از رسم است و حتما باید از کاغذ شطرنجی استفاده کنیم یا اندازه گیری دقیق انجام دهیم، اما روش ب سریع تر ما را به پاسخ یعنی مختصات c می رساند.
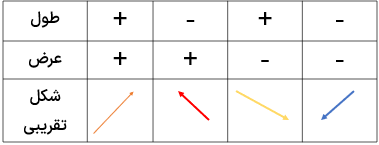
می دانیم اگر طول و عرض یک بردار هر دو مثبت باشند.شکل تقریبی آن به صورت روبرو خواهد بود،حال می توانیم جدول زیر را کامل کنیم:



1736019749.png)