درسنامه کامل ریاضی هشتم فصل 3 چندضلعی ها
تعداد بازدید : 7.59Mخلاصه نکات ریاضی هشتم فصل 3 چندضلعی ها - درسنامه شب امتحان ریاضی هشتم فصل 3 چندضلعی ها - جزوه شب امتحان ریاضی هشتم نوبت اول فصل 3 چندضلعی ها
چند ضلعی ها و تقارن
یادآوری
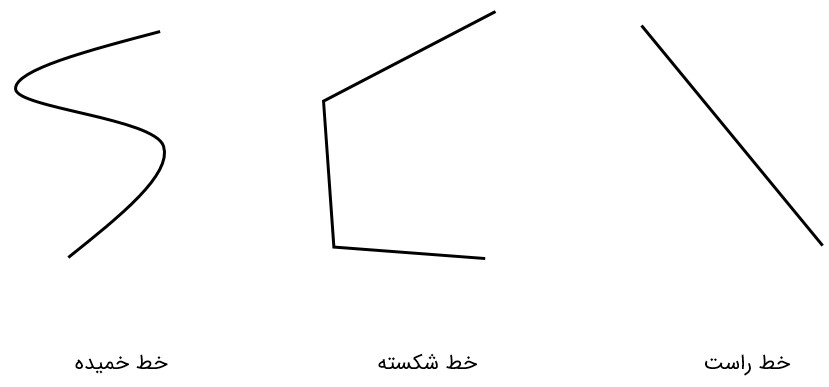
همانطور که در سال های قبل آموختیم خط ها را می توان به سه دسته تقسیم کرد:
چند ضلعی
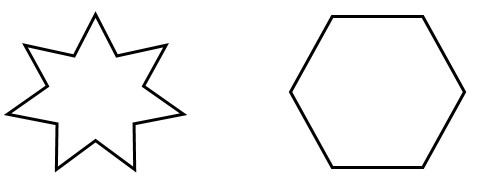
به هر خط شکسته بسته، با این شرط که ضلع ها یکدیگر را قطع نکنند مگر در رأس ها که دو ضلع به هم می رسند چندضلعی می گویند؛ مانند:
مثال
آیا شکل های زیر هر کدام یک چندضلعی هستند؟ چرا؟
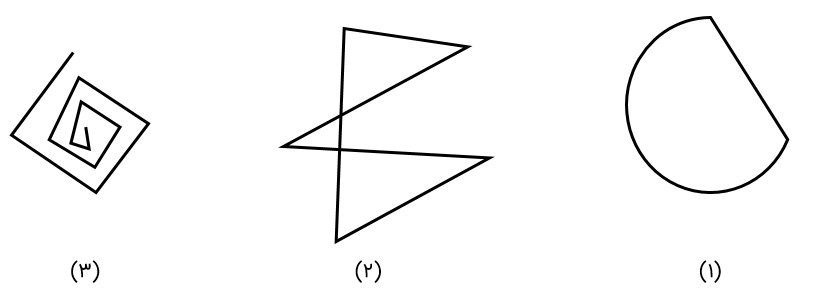
خیر:
شکل (1) چند ضلعی نیست؛ زیرا خط شکسته نیست.
شکل (2) چند ضلعی نیست؛ زیرا ضلع ها در جایی غیر از رأسها یکدیگر را قطع می کنند.
شکل (3) چند ضلعی نیست؛ زیرا خط شکسته بسته نیست.
تهیه کننده: افسانه پهلیانی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
چندضلعی ها
چندضلعی ها
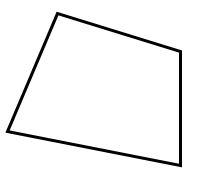
1- چند ضلعی محدب (کوژ):
چندضلعی که تمام زاویه هایش، هرکدام کمتر از \(180^∘\) باشد، چندضلعی محدب یا کوژ نام دارد؛ مانند:
2- چندضلعی مقعر (کاو):
چندضلعی که حداقل یکی از زاویه هایش بیشتر از \(180^∘\) باشد، چندضلعی مقعر یا کاو نام دارد؛ مانند:
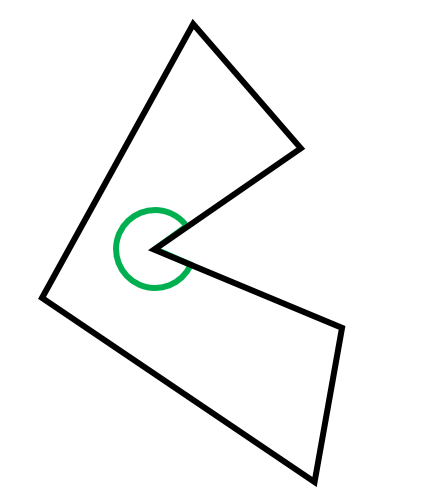
1 در چندضلعی های محدب هر دو نقطۀ دلخواه را بهم وصل کنیم تمام خط ایجاد شده در درون شکل قرار می گیرد؛ مانند:
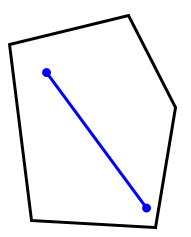
2 اما در چندضلعی های مقعر حداقل دو نقطه وجود دارد که اگر بهم وصل کنیم تمام خط و یا قسمتی از آن در درون شکل قرار نمی گیرد؛ مانند:
مثال
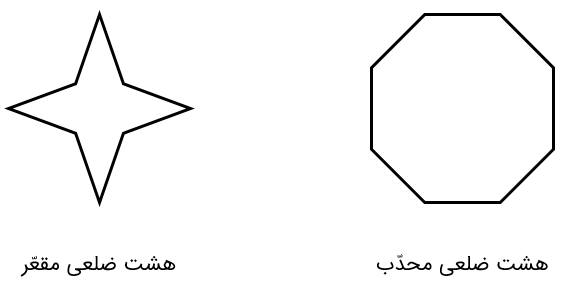
یک هشت ضلعی محدب و یک هشت ضلعی مقعر رسم کنید.
3- چندضلعی های منتظم:
اگر در یک چندضلعی همۀ زاویه ها با هم و همۀ ضلع ها نیز با هم مساوی باشند، چندضلعی منتظم است؛ مانند:
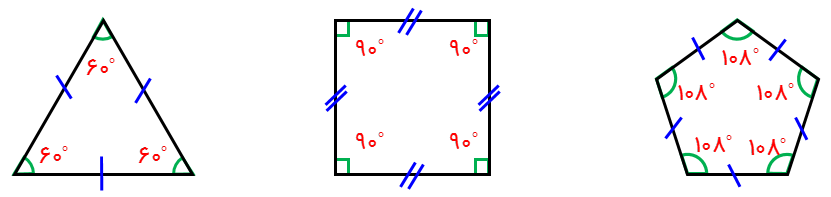
کدام گزینه یک شکل منتظم است؟
الف) لوزی
ب) مثلث متساوی الساقین
ج) مستطیل
د) مثلث متساوی الاضلاع
جواب صحیح گزینه «د» می باشد:
در مثلث متساوی الاضلاع، تمام زوایای داخلی مثلث برابر \(60^∘\) می باشد و اندازه تمام اضلاع آن، با هم برابر هستند.
1 در چندضلعی های منتظم هر چه تعداد ضلع ها بیشتر شود، اندازۀ زاویه ها بزرگتر می شود.
2 در چندضلعی های منتظم هر چه تعداد ضلع ها بیشتر شود، شکل بیشتر به دایره شبیه می شود.
تهیه کننده: افسانه پهلیانی
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم فصل 1 عددهای صحیح و گویا
جزوه جامع ریاضی هشتم فصل 2 عددهای اول
جزوه جامع ریاضی هشتم فصل 3 چندضلعی ها
جزوه جامع ریاضی هشتم فصل 4 جبر و معادله
جزوه جامع ریاضی هشتم فصل 5 بردار و مختصات
جزوه جامع ریاضی هشتم فصل 6 مثلث
جزوه جامع ریاضی هشتم فصل 7 توان و جذر
جزوه جامع ریاضی هشتم فصل 8 آمار و احتمال
جزوه جامع ریاضی هشتم فصل 9 دایره
تقارن
مرکز تقارن
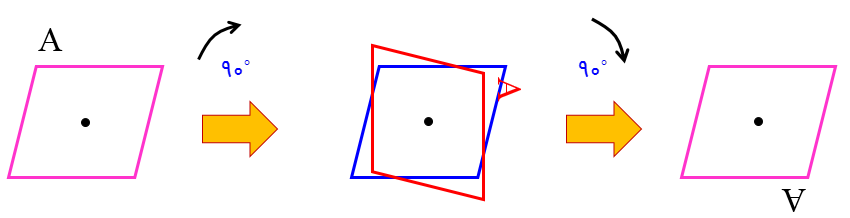
اگر شکلی را حول نقطه ای که درون خود شکل قرار دارد، \({180^ \circ }\) دوران دهید و نتیجۀ دوران روی خودش منطبق شود، آن نقطه مرکز تقارن شکل است. به عنوان مثال به شکل زیر نگاه کنید. ملاحظه می کنید شکل بعد از دوران \({180^ \circ }\) حول نقطه مشخص شده دوباره بر خودش منطبق شده است؛ پس نقطۀ مشخص شده مرکز تقارن است:
اما در شکل زیر ملاحظه می کنید شکل بعد از \({180^ \circ }\) دوران حول نقطۀ مشخص شده دوباره بر خودش منطبق نمی شود. پس نقطۀ مشخص شده مرکز تقارن نیست.
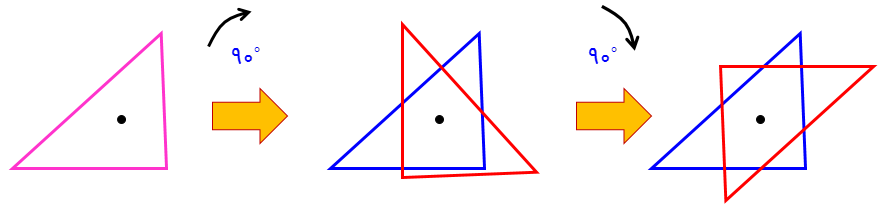
.
روشی دیگر برای تعیین مرکز تقارن
نقاطی را روی شکل تعیین کنید و قرینۀ آن نقاط را نسبت به مرکز مشخص شده بیابید. اگر نقطه ایی وجود داشت که قرینه اش روی شکل قرار نگرفت، نتیجه بگیرید مرکز تقارن نیست.
یادآوری
برای بدست آوردن قرینۀ هر نقطه از شکل، ابتدا آن را به نقطۀ مشخص شده درون شکل وصل می کنید و به اندازۀ خودش و در همان راستا امتداد می دهید؛ مثلاً:

با استفاده از همین روش تعیین کنید در کدامیک از شکل های زیر نقطۀ O مرکز تقارن است.
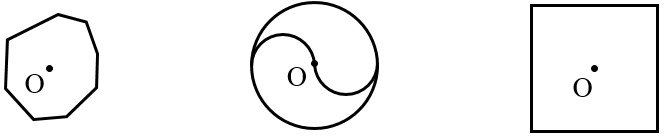
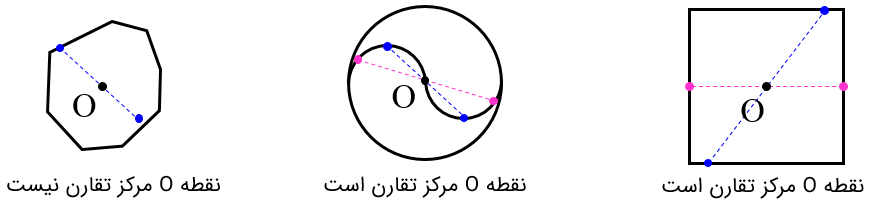
1 به طور کلی در چندضلعی های منتظم که تعداد ضلع ها زوج باشد مرکز تقارن وجود دارد؛ مانند مربع و ده ضلعی منتظم.
2 به طور کلی در چندضلعی های منتظم که تعداد ضلعها فرد باشد مرکز تقارن وجود ندارد؛ مانند پنج ضلعی منتظم و هفت ضلعی منتظم.
مثال
کدام یک از شکل های زیر مرکز تقارن دارد؟
الف نیم دایره
ب مثلث متساوی الاضلاع
ج نه ضلعی منتظم
د متوازی الاضلاع
پاسخ صحیح گزینه «د» می باشد:
متوازی الاضلاع دارای مرکز تقارن می باشد.
محور تقارن
خطی که شکل را به دو قسمت مساوی تقسیم می کند به طوری که اگر شکل را از روی آن خط تا بزنیم دو قسمت بر هم منطبق می شوند، و هر قسمت همانند آینه ای است برای قسمت دیگر؛ مانند:
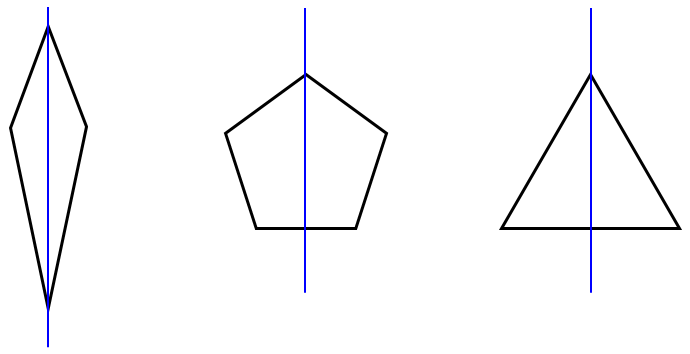
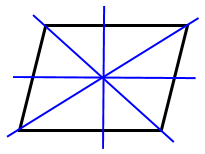
1 ممکن است شکلی مرکز تقارن نداشته باشد ولی محور تقارن داشته باشد؛ مانند مثلث متساوی الساقین:
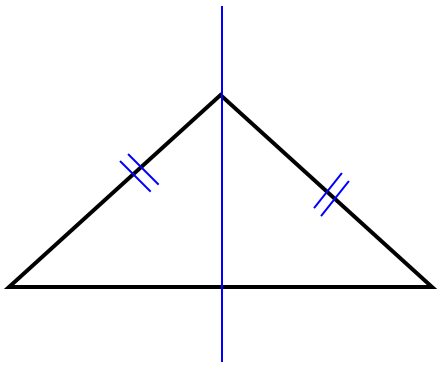
2 ممکن است شکلی مرکز تقارن داشته باشد ولی محور تقارن نداشته باشد؛ مانند متوازی الاضلاع:
مثال
هفت ضلعی منتظم هفت محور تقارن دارد (مرکز تقارن ندارد) و ده ضلعی منتظم ده محور تقارن دارد (مرکز تقارن دارد)
نسبت تعداد محور تقارن یک هشتضلعی منتظم به یک ششضلعی منتظم برابر است با ............ .

تهیه کننده:افسانه پهلیانی
دوران
دوران
اگر شکلی را روی صفحه حول یک نقطۀ ثابت (مرکز دوران) با زاویهای مشخص بچرخانیم تصویر حاصل دوران یافتۀ شکل می باشد.
1 در دوران \({180^ \circ }\) و \({360^ \circ }\) نیاز به مشخص کردن جهت دوران نیست ولی اگر زاویۀ دوران \({180^ \circ }\) و \({360^ \circ }\) نباشد باید جهت دوران مشخص شود.
2 در هر دوران تصویر بدست آمده (دوران یافته) هم اندازه و همنهشت با شکل است:
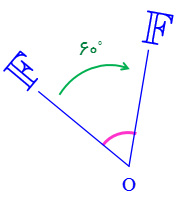
دوران 60 درجه در جهت حرکت عقربه های ساعت.
تقارن چرخشی (دورانی) در چندضلعی های منتظم
اگر سه ضلعی منتظم (مثلث متساوی الاضلاع) را حول مرکز O با زاویۀ دوران \({120^ \circ }\) دوران دهیم بر خودش منطبق می شود.
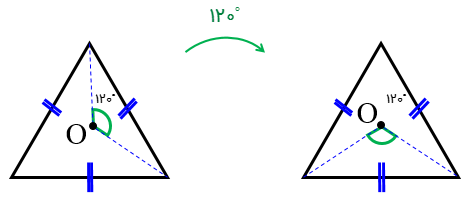
حداقل زاویۀ دوران در تقارن چرخشیِ چندضلعی های منتظم را می توان از دستور زیر بدست آورد:
\((0 < \alpha \le {360^ \circ })\)
\(\alpha = {360^ \circ } \div \)تعداد ضلع
سایر دورانها مضرب های \(\alpha \) هستند.
مثال
سه ضلعی منتظم (مثلث متساوی الاضلاع) با چه دورانه ایی حول نقطۀ O بر خودش منطبق می شود؟
\({360^ \circ } \div 3 = {120^ \circ } \Rightarrow \alpha = {120^ \circ }\,,\,{240^ \circ }\,,\,{360^ \circ }\)
در کدام یک از گزینه های زیر چندضلعی منتظم با دوران 90 درجه حول نقطۀ مشخص شده در جهت حرکت عقربه های ساعت بر خودش منطبق می شود؟

جواب صحیح گزینه «الف» می باشد:
\({360^ \circ } \div 8 = {45^ \circ } \Rightarrow \alpha = {45^ \circ }\,,\,{90^ \circ }\,,\,{135^ \circ }\)
هشت ضلعی منتظم با دوران های \({45^ \circ }\,,\,{90^ \circ }\,,\,{135^ \circ }\,,\,{180^ \circ }\,,\,{225^ \circ }\,,\,{270^ \circ }\,,\,{315^ \circ }\,,\,{360^ \circ }\) حول نقطۀ مشخص شده بر خودش منطبق می شود.
تهیه کننده:افسانه پهلیانی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
توازی و تعامد
توازی و تعامد
دو خط متمایز در صفحه نسبت به هم دو حالت دارند:
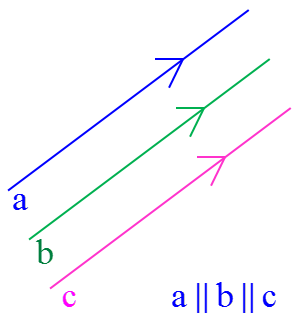
1) دو خط موازی هستند و هیچ نقطه مشترکی ندارند:

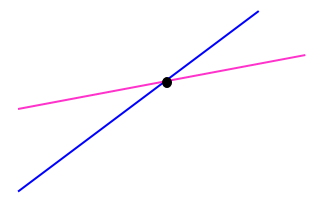
2) دو خط متقاطع اند و یک نقطه مشترک دارند:
1 برای اینکه خطوط موازی را نشان دهیم روی آنها علامت های یکسان (<) یا (<<) یا (<<<) یا ... قرار می دهیم و بین اسامی آنها از علامت (||) استفاده می کنیم:
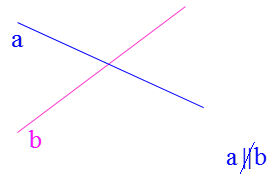
2 اگر خطوط داده شده موازی نباشند و متقاطع باشند بین اسامی آنها از علامت \({\parallel } \) استفاده می کنیم:
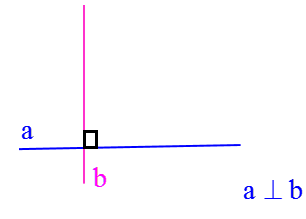
3 اگر خطوط متقاطع بر هم عمود باشند بین اسامی آنها از علامت \( \bot \) استفاده می کنیم:
دو خط موازی
در دورۀ ابتدایی آموختید که دو خط موازی هیچگاه یکدیگر را قطع نمیکنند ممکن است این پرسش در ذهن شما بوجود بیاید که :برای تشخیص موازی بودن دو خط باید تا کجا آن دو را ادامه دهیم که مطمئن شویم موازی هستند؟ و اما در ادامه روشی را معرفی میکنیم که برای تشخیص موازی بودن دو خط مفید است.
تعریف دیگری برای دو خط موازی
هرگاه خطی مانند d، دو خط a و b را قطع کند و زاویه های مساوی ایجاد کند، نتیجه می گیریم دو خط a و b موازی هستند.
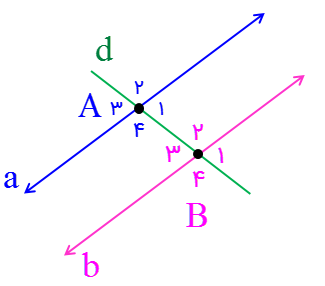
\({\hat A_1} = {\hat A_3} = {\hat B_1} = {\hat B_3}\)(زاویه های تند مساویند)
\({\hat A_2} = {\hat A_4} = {\hat B_2} = {\hat B_4}\)(زاویه های باز مساویند)
\( \Rightarrow a\parallel b\)
به عنوان مثال:
در شکل مقابل خط d دو خط a و b را طوری قطع کرده که زاویه های مساوی ایجاد کرده است پس دو خط a و b موازیند:
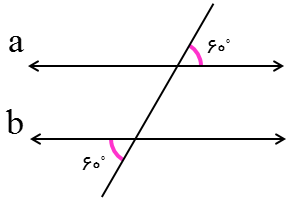
زاویه های تند\( = {60^ \circ }\)
زاویه های باز\( = {120^ \circ }\)
\( \Rightarrow a\parallel b\)
با توجه به شکل مقابل آیا دو خط a و b موازیند؟
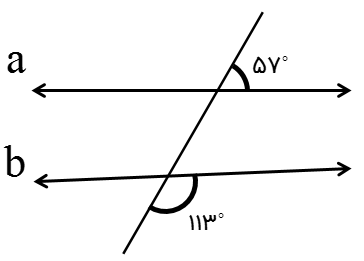
خیر؛ زیرا زاویه های تند با هم مساوی نیستند و زاویه های باز نیز با هم مساوی نیستند.
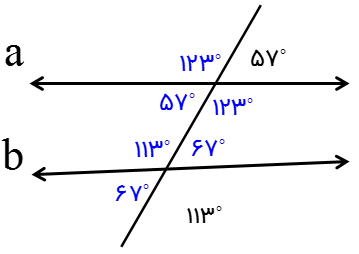
در نتیجه: \( \Rightarrow a{\parallel }b\)
اگر خط مورّبی دو خط موازی را قطع کند با آنها زاویه های مساوی می سازد.
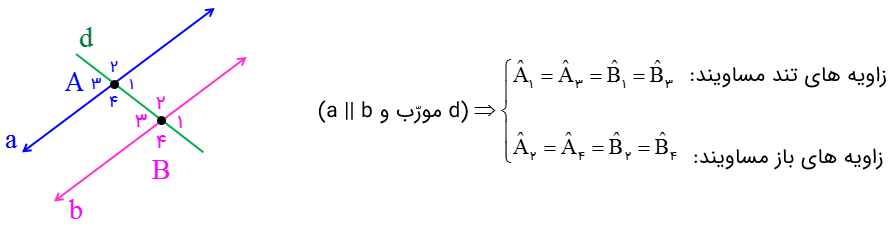
و هر زاویۀ باز با هر زاویۀ تند مکمل است:
\({\hat A_1} + {\hat B_3} = {180^ \circ }\)
دو خط a و b در شکل مقابل موازیند. اندازۀ زاویۀ خواسته شده را بدست آورید.
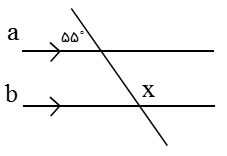
زاویۀ x زاویه ای باز است و مکمل \({55^ \circ }\) ؛ بنابراین: \(x = {180^ \circ } - {55^ \circ } + {125^ \circ }\)
با توجه به دو خط موازی اندازۀ زاویه های خواسته شده را بدست آورید
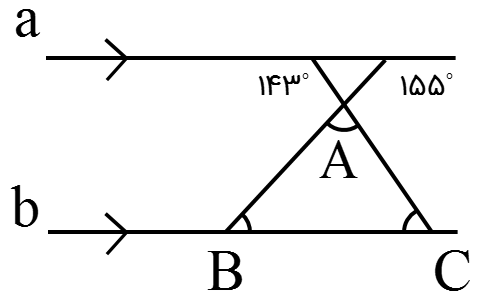
\(\hat A = \,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\hat B = \,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\hat C = \)
اگر شکل را به دو قسمت زیر تقسیم کنیم:
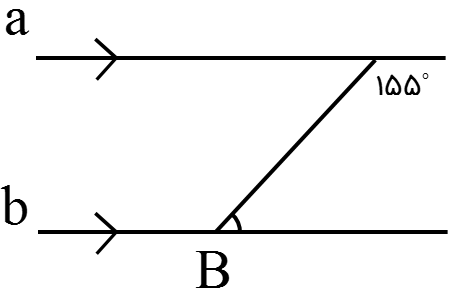
در این قسمت \(\hat B\) مکمل زاویه \({155^ \circ }\) است:
\(\hat B = {180^ \circ } - {155^ \circ } = {25^ \circ }\)
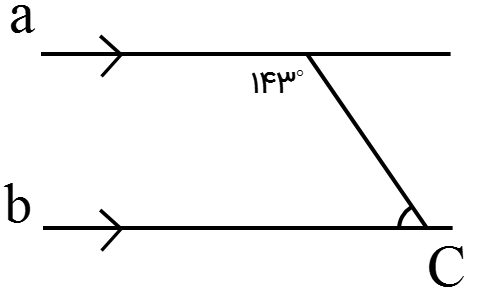
در این قسمت \(\hat C\) مکمل زاویه \({143^ \circ }\) است:
\(\hat C = {180^ \circ } - {143^ \circ } = {37^ \circ }\)
برای بدست آوردن \(\hat A\) با توجه به اینکه مجموع زوایای داخلی هر مثلث \({180^ \circ }\) است، داریم:
\(\hat A = {180^ \circ } - (\hat B + \hat C) = {180^ \circ } - ({25^ \circ } + {37^ \circ }) = {180^ \circ } - {62^ \circ } = {118^ \circ }\)
شکل مقابل با توجه به موازی بودن دو خط مقدار x را تعیین کنید.
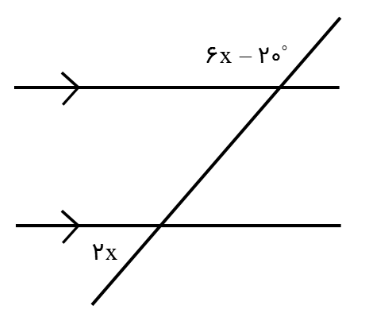
2x اندازۀ زاویۀ تند و \(6x - {20^ \circ }\) اندازۀ باز است دو زاویه مکمل یکدیگر هستند یعنی:
\(6x - {20^ \circ } + 2x = {180^ \circ }\)
سپس با معادله x را تعیین می کنیم:
\(\begin{array}{l}8x - {20^ \circ } = {180^ \circ } \Rightarrow 8x = {180^ \circ } + {20^ \circ } = {200^ \circ }\\\\ \Rightarrow x = \frac{{{{200}^ \circ }}}{8} \Rightarrow x = {25^ \circ }\end{array}\)
نکاتی در مورد خطوط موازی:
1 دو خط عمود بر یک خط، با هم موازیند.
\(\left\{ \begin{array}{l}a \bot d\\\\b \bot d\end{array} \right. \Rightarrow a\parallel b\)
2 دو خط موازی با یک خط، با هم موازیند.
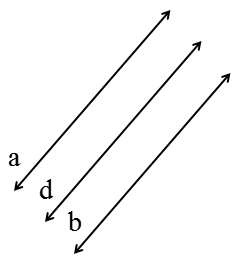
\(\left\{ \begin{array}{l}a\parallel d\\\\b\parallel d\end{array} \right. \Rightarrow a\parallel b\)
3 اگر خطّی بر یکی از دو خطّ موازی عمود باشد، بر دیگری نیز عمود خواهد بود.
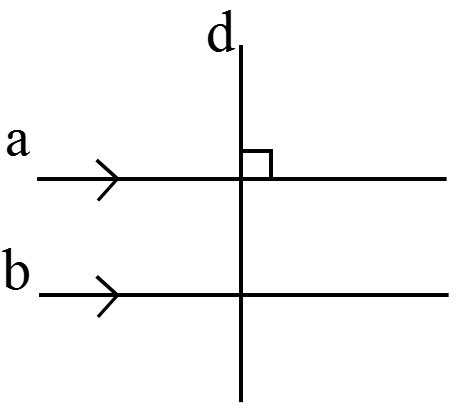
\(\left\{ \begin{array}{l}a \bot d\\\\a\parallel b\end{array} \right. \Rightarrow d \bot b\)
4 در متوازی الاضلاع، ضلع های رو به رو با هم موازیند با کمک روابط موجود بین خطوط موازی و مورّب که در این درس آموختید، می توان نتیجه گرفت در هر متوازی الاضلاع زاویه های رو به رو با هم برابرند و زاویه های مجاور مکمل اند.
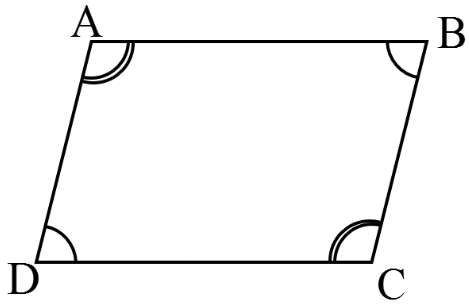
\(\begin{array}{l}\left\{ \begin{array}{l}\hat A = \hat C\\\\\hat D = \hat B\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\hat A + \hat B = {180^ \circ }\\\\\hat B + \hat C = {180^ \circ }\end{array} \right.\,\,\,\,\,\,\left\{ \begin{array}{l}\hat C + \hat D = {180^ \circ }\\\\\hat D + \hat A = {180^ \circ }\end{array} \right.\\\end{array}\)
با توجه به اینکه شکل مقابل متوازی الاضلاع ست، مقدار x را تعیین کنید.
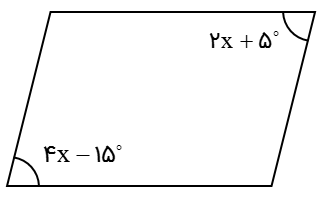
در متوازی الاضلاع دو زاویه رو به رو با هم مساوی هستند.
\(2x + {5^ \circ } = 4x - {15^ \circ }\)
به کمک حل معادله، مقدار x را تعیین می کنیم:
\(\begin{array}{l}2x + {5^ \circ } = 4x - {15^ \circ } \Rightarrow 4x - 2x = {5^ \circ } + {15^ \circ }\\\\ \Rightarrow 2x = {20^ \circ } \Rightarrow x = \frac{{{{20}^ \circ }}}{2} \Rightarrow x = {10^ \circ }\end{array}\)
1 هر جا خطوط موازی را به صورت حرف Z و یا حرف N دیدیم و یا برعکس آنها، زاویه های تند آنها با هم مساویند؛ مانند:

اندازۀ زاویه x چند درجه است؟
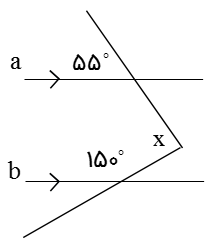
1) \({55^ \circ }\) 2) \({30^ \circ }\) 3) \({95^ \circ }\) 4) \({85^ \circ }\)
پاسخ صحیح گزینه 4 می باشد:
می توان با رسم خطی موازی دو خط شکل را به صورت مقابل تقسیم کنیم:
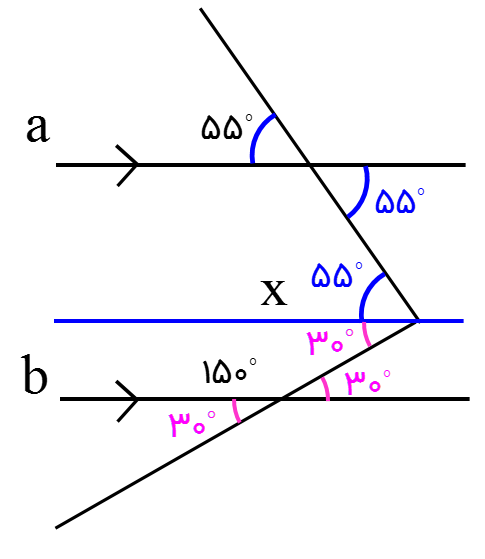
\(x = {55^ \circ } + {30^ \circ } = {85^ \circ }\)
تهیه کننده: افسانه پهلیانی
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم فصل 1 عددهای صحیح و گویا
جزوه جامع ریاضی هشتم فصل 2 عددهای اول
جزوه جامع ریاضی هشتم فصل 3 چندضلعی ها
جزوه جامع ریاضی هشتم فصل 4 جبر و معادله
جزوه جامع ریاضی هشتم فصل 5 بردار و مختصات
جزوه جامع ریاضی هشتم فصل 6 مثلث
جزوه جامع ریاضی هشتم فصل 7 توان و جذر
جزوه جامع ریاضی هشتم فصل 8 آمار و احتمال
جزوه جامع ریاضی هشتم فصل 9 دایره
متوازی الاضلاع
متوازی الاضلاع
متوازی الاضلاع چهارضلعی است که اضلاع رو به رو دو به دو موازی باشند.
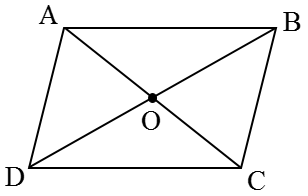
با استفاده از کاغذ پوستی و دوران \({180^ \circ }\) حول مرکز تقارنش (نقطۀ O) مشاهده می کنید که اضلاع رو به رو، روی هم قرار می گیرند (پس با هم برابرند) و زاویه های رو به رو نیز روی هم قرار می گیرند (پس با هم برابرند). با استفاده از دوران و انطباق میتوان ویژگی های متوازی الاضلاع را به صورت زیر نوشت:
1) در هر متوازی الاضلاع، اضلاع رو به رو با هم مساویند:
AB=DC , AD=BC
2) در هر متوازی الاضلاع، زاویه های رو به رو با هم مساویند:
\(\hat A = \hat C\,\,\,,\,\,\,\hat B = \hat D\)
3) در هر متوازی الاضلاع، زاویه های مجاور به یک ضلع مکمل ند:
\(\begin{array}{l}\hat A + \hat B = {180^ \circ }\,\,\,,\,\,\,\hat B + \hat C = {180^ \circ }\\\\\hat C + \hat D = {180^ \circ }\,\,\,,\,\,\,\hat D + \hat A = {180^ \circ }\end{array}\)
4) در هر متوازی الاضلاع، قطرها یکدیگر را نصف می کنند:
AO=OC , BO=OD
5) در هر متوازی الاضلاع، محل برخورد قطرها، مرکز تقارن متوازی الاضلاع است (نقطۀ O)
متوازی الاضلاع، محور تقارن ندارد.
مثال
با توجه به متوازی الاضلاع مقابل مقادیر خواسته شده را بدست آورید.
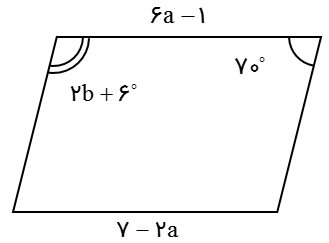
a=… b=…
می دانیم در متوازی الاضلاع، ضلع های رو به رو با هم برابرند. پس 6a-1=7-2a. به کمک حل معادله مقدار a را تعیین می کنیم:
\(6a + 2a = 7 + 1 \Rightarrow 8a = 8 \Rightarrow a = \frac{8}{8} \Rightarrow a = 1\)
می دانیم در متوازی الاضلاع،زاویه های مجاور به یک ضلع مکمل ند. پس \(2b + {6^ \circ } + {70^ \circ } = {180^ \circ }\). به کمک حل معادله مقدار b را تعیین می کنیم:
\(2b = {180^ \circ } - {76^ \circ } = {104^ \circ } \Rightarrow b = \frac{{{{104}^ \circ }}}{2} \Rightarrow b = {52^ \circ }\)
\(2b + {6^ \circ } + {70^ \circ } = {180^ \circ }\)
تهیه کننده : افسانه پهلیانی
مستطیل و لوزی
مستطیل
اگر در متوازی الاضلاع، زاویه ها قائمه \(({90^ \circ })\) باشند، مستطیل بوجود می آید. بنابراین مستطیل، متوازی الاضلاعی است که زاویه های قائمه دارد.
اگر مستطیلی را روی یکی از خط های تقارنش و سپس روی خط تقارن دیگرش تا کنید، می توان ویژگی های مستطیل را به صورت زیر نوشت:
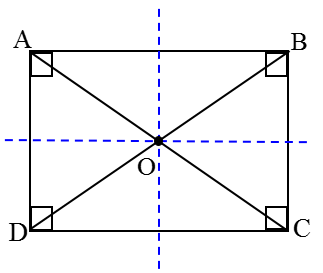
1) در هر مستطیل، همۀ زاویه ها با هم برابرند:
\(\hat A = \hat B = \hat C = \hat D = {90^ \circ }\)
2) در هر مستطیل، ضلع های رو به رو با هم برابرند:
AB=DC , AD=BC
3) در هر مستطیل، قطرها با هم برابرند:
AC=BD
4) در هر مستطیل، قطرها یکدیگر را نصف می کنند:
OA=OB=OC=OD
هر مستطیل دو محور تقارن دارد:
1 خطی که از وسط طول ها می گذرد.
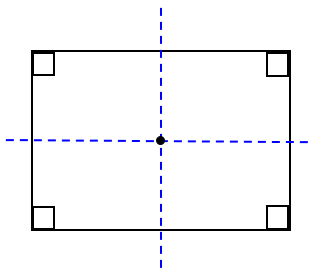
2 خطی که از وسط عرض ها می گذرد.
1 قطرها در مستطیل محور تقارن نیستند.
2 در مستطیل قطرها بر هم عمود نیستند.
لوزی
اگر در متوازی الاضلاع، همۀ ضلع ها برابر باشند. لوزی به وجود می آید. بنابراین لوزی، متوازی الاضلاعی است که ضلع های برابر دارد:
\(\overline {AB} = \overline {BC} = \overline {CD} = \overline {DA} \)
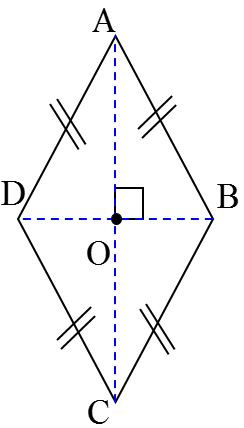
با توجه به اینکه لوزی نوعی متوازی الاضلاع است، علاوه بر همۀ ویژگی های متوازی الاضلاع، ویژگی دیگری نیز دارد:
«در هر لوزی قطرها بر هم عمودند.» یعنی:
\(\overline {AC} \bot \overline {BD} \)
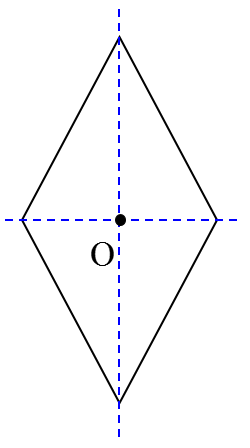
در هر لوزی قطرها محور تقارن هستند و محل برخورد قطرها، مرکز تقارن (نقطۀ O) لوزی است.
تهیه کننده:افسانه پهلیانی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم
مربع و ذوزنقه
مربع
اگر در متوازی الاضلاع، همه ضلع ها هم اندازه و همه زاویه ها قائمه باشند، مربع به وجود می آید. بنابراین مربع، متوازی الاضلاعی است که هم ضلع های مساوی و هم زاویه های قائمه دارد.
\(\begin{array}{l}\overline {AB} = \overline {BC} = \overline {CD} = \overline {DA} \\\\\hat A = \hat B = \hat C = \hat D = {90^ \circ }\end{array}\)
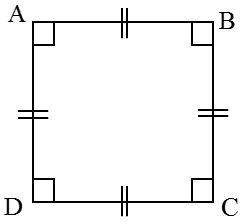
در مربع تمام ویژگی های یک متوازی الاضلاع وجود دارد علاوه بر همۀ ویژگی های متوازی الاضلاع، ویژگی های زیر را هم دارد:
1) در هر مربع قطرها با هم برابرند: AC=BD
2) در هر مربع قطرها بر هم عمودند: \(AC \bot BD\)
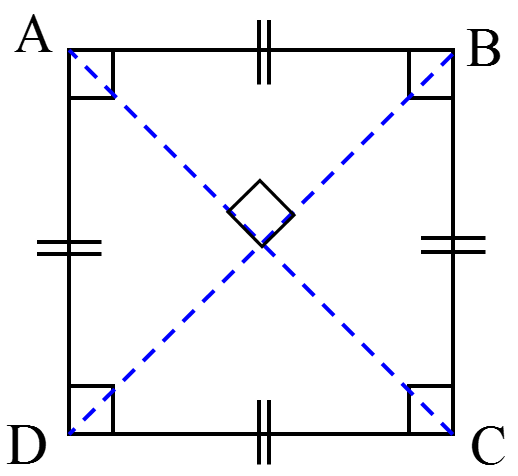
1 هر مربع 4 محور تقارن دارد:
الف دو قطر
ب خطوطی که از وسط هر دو ضلع رو به رو می گذرند.
محل برخورد خط های تقارن، مرکز تقارن (نقطۀ O) مربع است.
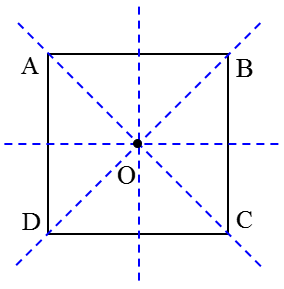
2 هر مربع هم نوعی متوازی الاضلاع، هم نوعی لوزی و هم نوعی مستطیل است. زیرا ویژگی های متوازی الاضلاع، لوزی و مستطیل را دارد.
3 اگر وسط های اضلاع یک مربع را به صورت متوالی به هم وصل کنیم شکل بوجود آمده باز هم مربع خواهد بود (با استفاده از خط های تقارن در مربع و تا زدن مربع روی این خطوط می توان به درستی این مطلب پی برد).
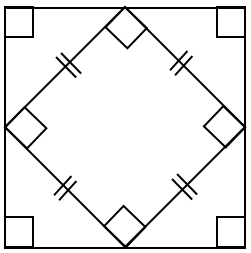
4 اگر وسط های اضلاع یک مستطیل را به صورت متوالی به هم وصل کنیم شکل بوجود آمده یک لوزی خواهد بود (با استفاده از خط های تقارن در مستطیل و تا زدن مستطیل روی این خطوط می توان به درستی این مطلب پی برد).
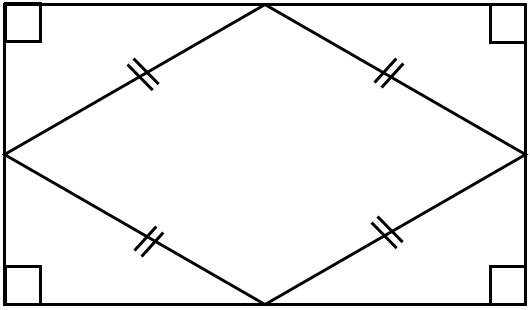
5 اگر وسط های اضلاع یک متوازی الاضلاع را به صورت متوالی به هم وصل کنیم شکل بوجود آمده، یک متوازی الاضلاع خواهد بود.
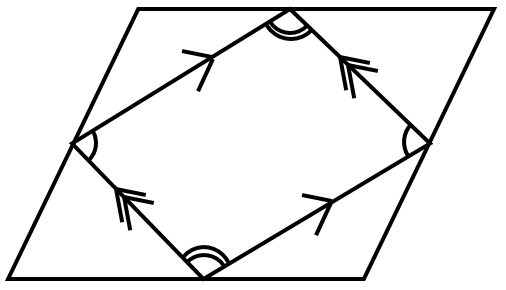
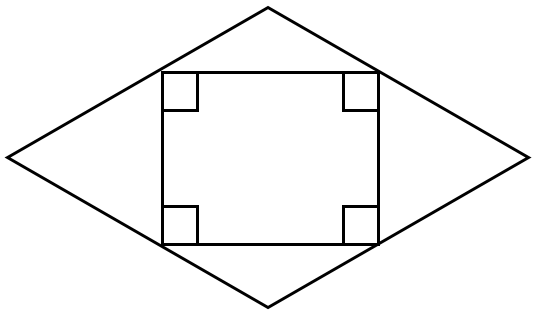
6 اگر وسط های اضلاع یک لوزی را به صورت متوالی به هم وصل کنیم شکل بوجود آمده، یک مستطیل خواهد بود.
مثال
در شکل مقابل، ABCD مستطیل و DCEF متوازی الاضلاع است. مقدار زاویۀ \(\hat x\) چند درجه است؟
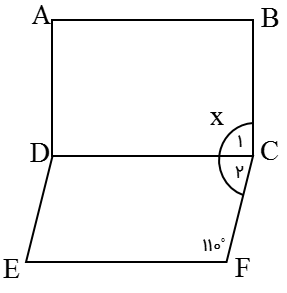
\(\left. \begin{array}{l}\hat x = {{\hat C}_1} + {{\hat C}_2}\\\\{{\hat C}_1} = {90^ \circ }\\\\{{\hat C}_2} + {110^ \circ } = {180^ \circ } \Rightarrow {{\hat C}_2} = {70^ \circ }\end{array} \right\} \Rightarrow \hat x = {90^ \circ } + {70^ \circ } = {160^ \circ }\)
جاهای خالی را با عبارت مناسب پر کنید.
1 اگر وسط های اضلاع یک مستطیل را به طور متوالی به هم وصل کنیم، شکل حاصل ................ خواهد بود.
لوزی
2 در متوازی الاضلاع، محل برخورد قطرها، .................... شکل است.
مرکز تقارن
3 لوزی که دو قطر مساوی دارد، ..................... نام دارد.
مربع
4 متوازی الاضلاعی که یک زاویۀ قائمه دارد ................... نام دارد.
مستطیل
ذوزنقه
چهارضلعی که فقط دو ضلع موازی دارد، ذوزنقه نام دارد (AB||DC).
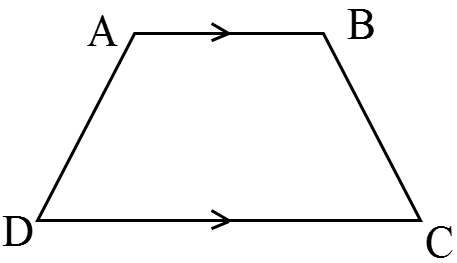
به دو ضلع موازی قاعده و به دو ضلع دیگر که با هم موازی نیستند، ساق می گویند.
در ذوزنقه زاویه های رو به رو با هم مساوی نیستند و قطرها یکدیگر را نصف نمی کنند.
1 در هر ذوزنقه دو زاویۀ مجاور به هر ساق (که با یک ضلع مورّب در ارتباط هستند) مکملند:
\(\hat A + \hat D = {180^ \circ }\,\,\,,\,\,\,\hat B + \hat C = {180^ \circ }\)
2 اگر در ذوزنقه دو ساق مساوی باشند، ذوزنقه متساوی الساقین خواهد بود.
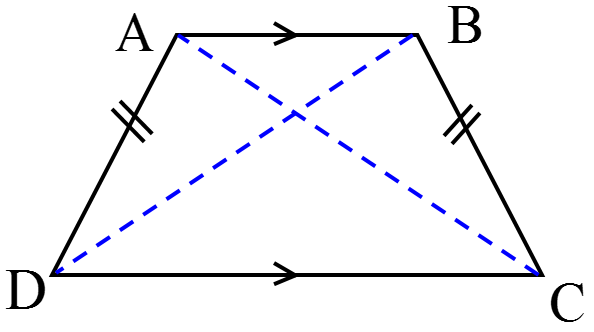
پس دو زاویۀ مجاور به هر قاعده با هم برابرند:
\(\overline {AD} = \overline {BC} \,\,\,,\,\,\,\hat A = \hat B\,\,\,,\,\,\,\hat D = \hat C\)
و دو قطر نیز با هم برابرند:
AC=BD
3 ذوزنقه متساوی الساقین یک خط تقارن دارد:
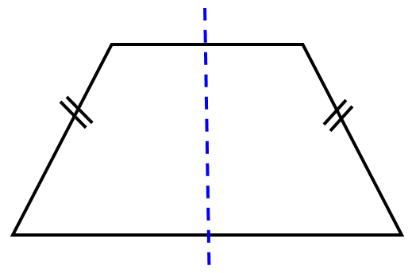
4 اگر در ذوزنقه یکی از ساق ها بر دو قاعده عمود باشد، ذوزنقه قائم الزاویه خواهد بود:
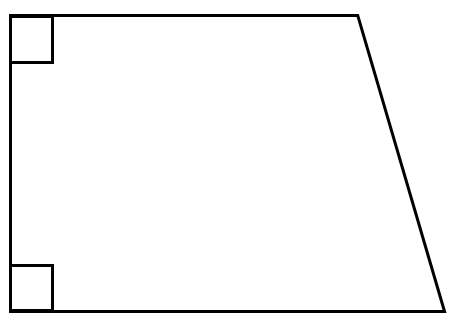
تهیه کننده:افسانه پهلیانی
جزوات جامع پایه هشتم
جزوه جامع ریاضی هشتم فصل 1 عددهای صحیح و گویا
جزوه جامع ریاضی هشتم فصل 2 عددهای اول
جزوه جامع ریاضی هشتم فصل 3 چندضلعی ها
جزوه جامع ریاضی هشتم فصل 4 جبر و معادله
جزوه جامع ریاضی هشتم فصل 5 بردار و مختصات
جزوه جامع ریاضی هشتم فصل 6 مثلث
جزوه جامع ریاضی هشتم فصل 7 توان و جذر
جزوه جامع ریاضی هشتم فصل 8 آمار و احتمال
جزوه جامع ریاضی هشتم فصل 9 دایره
زاویه های داخلی
کاشی کاری
گاهی برای پوشاندن یک سطح از یک یا چند نوع کاشی استفاده می کنند به صورتی که کاشی ها روی هم قرار نگیرند و نیز بین آنها فضای خالی نباشد. مانند شکل های زیر:
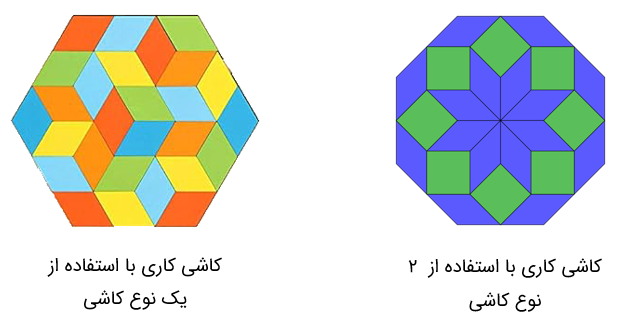
مثال
به شکل زیر توجه کنید. چرا کاشیکاری با یک نوع کاشی انجام نمی شود؟

زیرا بین کاشی ها فضای خالی وجود دارد.
سطح زیر با مثلث هایی همنهشت با مثلث ABC کاشی کاری شده است.
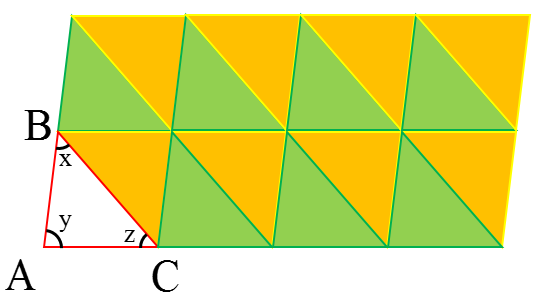
مثلث سبز انتقال یافته مثلث ABC است.
مثلث نارنجی دوران یافته مثلث ABC است.
اگر سه مثلث همنهشت را دوباره رسم کنیم:
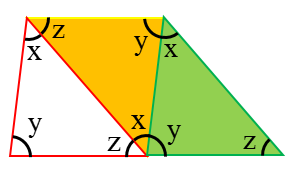
ملاحظه می کنید که سه زاویۀ x، y و z که زاویه های یک مثلث هستند در کنار هم تشکیل زاویۀ نیم صفحه را می دهند، پس:
مجموع زاویه های داخلی یک مثلث \({180^ \circ }\) است.
\(\hat A + \hat B + \hat C = {180^ \circ }\)
مجموع زاویه های داخلی یک چندضلعی
منظور از زاویه های داخلی یک چندضلعی، زاویه هایی است که درون چندضلعی قرار دارد و ضلع های زاویه، ضلع های چندضلعی است. برای محاسبه مجموع زاویه های داخلی چندضلعی با رسم تعدادی از قطرهای چندضلعی درون آن تعدادی مثلث ایجاد می کنیم و با توجه به اینکه: «مجموع زاویه های هر مثلث \({180^ \circ }\) است.» مجموع زاویه های داخلی چندضلعی را به دست می آوریم:
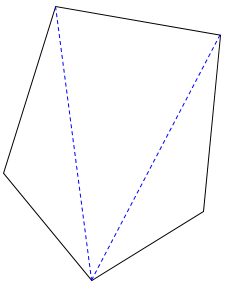
\(3 \times {180^ \circ } = {540^ \circ }\)
دقت کنید قطرهایی رسم کنید که یکدیگر را قطع نکنند (به جز در رأس). برای رسم قطرها یک رأس را در نظر می گیریم و به رأس های مقابل وصل می کنیم. با دقت در شکل بالا متوجه می شوید که تعداد مثلث های ایجاد شده در هر چندضلعی 2 تا از تعداد ضلع ها کمتر است. مثلاً مجموع زاویه های داخلی یک شش ضلعی برابر است با:
\((6 - 2) \times {180^ \circ } = 4 \times {180^ \circ } = {720^ \circ }\)
برای محاسبه مجموع زاویه های داخلی چندضلعی از رابطۀ زیر استفاده می کنیم:
180 × (2 – تعداد ضلع ها) = 180 × تعداد مثلث ها = مجموع زاویه های داخلی هر چند ضلعی
شکل مقابل مقدار a را بدست آورید.
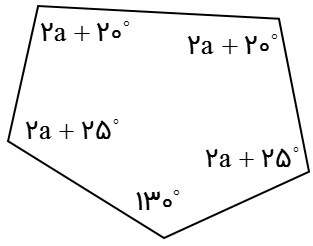
540 = 180 × 3 = مجموع زاویه های داخلی 5 ضلعی
\(\begin{array}{l}2a + {20^ \circ } + 2a + {20^ \circ } + 2a + {25^ \circ } + 2a + {25^ \circ } + {130^ \circ } = {540^ \circ }\\\\ \Rightarrow 8a + {220^ \circ } = {540^ \circ } \Rightarrow 8a = {540^ \circ } - {220^ \circ } = {320^ \circ }\\\\ \Rightarrow a = \frac{{{{320}^ \circ }}}{8} = {40^ \circ }\end{array}\)
محاسبۀ اندازۀ هر زاویۀ داخلی یک چندضلعی منتظم
ابتدا مجموع زاویه های داخلی چندضلعی منتظم را بدست می آوریم و چون در شکل های منتظم زاویه ها با هم برابرند، مجموع زاویه های داخلی را بر تعداد زاویه ها تقسیم می کنیم تا اندازۀ هر زاویه بدست آید.
مثال
اندازۀ هر زاویۀ داخلی هشت ضلعی منتظم را بدست آورید.
1080 = 180 × (2 – 8) = مجموع زاویه های داخلی 8 ضلعی منتظم
135 = 8 ÷ 1080 = اندازه هر زاویه داخلی هشت ضلعی منتظم
اندازۀ هر زاویۀ داخلی n ضلعی منتظم برابر است با \(\frac{{(n - 2) \times {{180}^ \circ }}}{n}\)
آیا با کاشی هایی به شکل شش ضلعی منتظم می توان به تنهایی کاشی کاری کرد؟
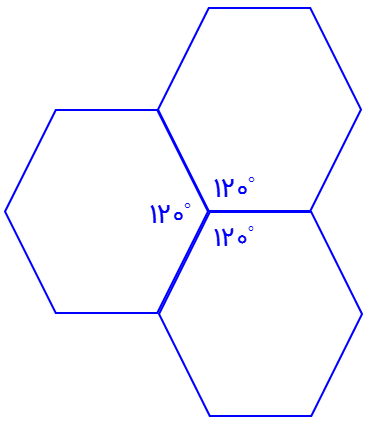
بله؛ در کاشی کاری با شش ضلعی منتظم به تنهایی، هیچ فضای خالی ایجاد نمی شود. ابتدا اندازۀ هر زاویۀ داخلی شش ضلعی منتظم را محاسبه می کنیم. شش ضلعی های منتظم وقتی کنار هم قرار می گیرند در هر گوشه \({120^ \circ }\)، زاویه دارند:
\(\frac{{(6 - 2) \times {{180}^ \circ }}}{6} = \frac{{4 \times {{180}^ \circ }}}{6} = \frac{{{{720}^ \circ }}}{6} = {120^ \circ }\)
سه تا زاویه \({120^ \circ }\) داریم که می شود \(3 \times {120^ \circ } = {360^ \circ }\).
اگر بخواهیم فقط با استفاده از یک نوع شکل منتظم کاشی کاری کنیم، اندازۀ هر زاویۀ داخلی آن باید شمارندۀ \({360^ \circ }\) باشد؛ به عبارتی \({360^ \circ }\) باید بر اندازۀ هر زاویۀ داخلی شکل منتظم بخش پذیر باشد.
آیا با کاشی هایی به شکل پنج ضلعی منتظم، می توان به تنهایی کاشی کاری کرد؟
اندازۀ هر زاویۀ داخلی \(\frac{{(5 - 2) \times {{180}^ \circ }}}{5} = \frac{{3 \times {{180}^ \circ }}}{5} = \frac{{{{540}^ \circ }}}{5} = {108^ \circ }\) می باشد و 360 بر 108 بخش پذیر نیست.
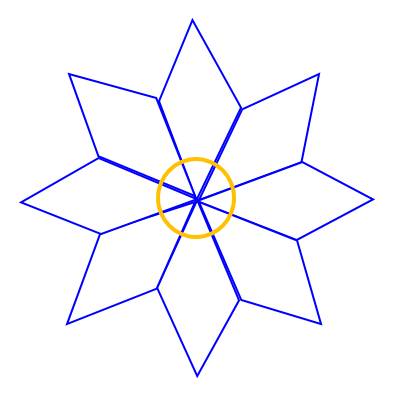
شکل زیر با یک نوع مثلث و یک نوع لوزی کاشی کاری شده است. اندازۀ زاویه های مثلث و لوزی را محاسبه کنید.

اگر به مرکز طرح کاشی کاری دقت کنید، 8 تا زاویۀ تند لوزی ها که با هم مساویند، در کنار هم تشکیل زاویۀ 360 درجه را می دهند. اندازۀ زاویۀ تند در هر لوزی برابر 45 درجه خواهد بود:
\(\frac{{{{360}^ \circ }}}{8} = {45^ \circ }\)
اندازۀ زاویۀ باز در هر لوزی 135 = 45 – 180 می باشد:
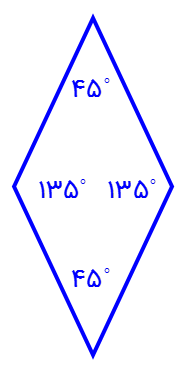
سپس به گوشه ای دقت کنید که از دو زاویۀ باز لوزی و یک زاویۀ مثلث تشکیل شده است. اندازۀ یکی از زاویه های مثلث برابر خواهد بود با:
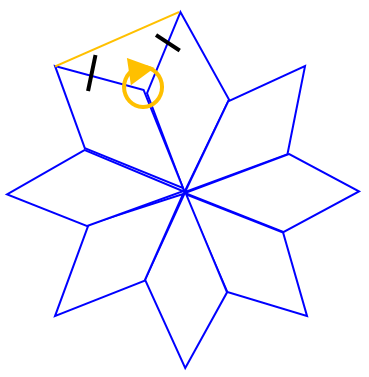
\(\begin{array}{l}2 \times {135^ \circ } = {270^ \circ }\\\\ \Rightarrow {360^ \circ } - {270^ \circ } = {90^ \circ }\end{array}\)
درمثلث قائم الزاویه ای که دو ساق برابر دارد اندازۀ هر زاویۀ تند برابر است با:
\({180^ \circ } - {90^ \circ } = {90^ \circ } \Rightarrow \frac{{{{90}^ \circ }}}{2} = {45^ \circ }\)
برای محاسبه مجموع زاویه های داخلی در n ضلعی های مقعر (کاو) نیز از رابطه \({180^ \circ } \times (n - 2)\) استفاده می کنیم.
تهیه کننده : افسانه پهلیانی
زاویه های خارجی
زاویه های خارجی
در چندضلعی های محدب، زاویه ای که در هر رأس بین یک ضلع و امتداد ضلع دیگر تشکیل می شود، زاویۀ خارجی آن رأس نامیده می شود؛ مانند:
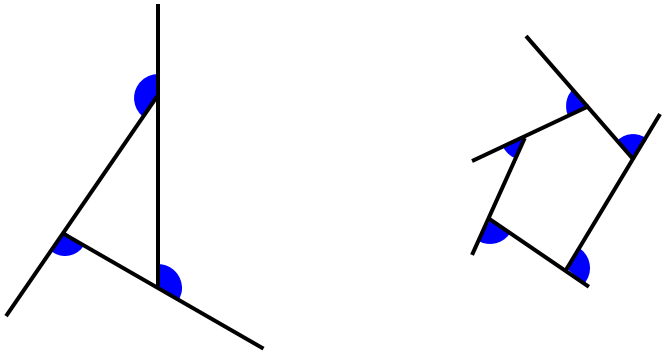
1 در چندضلعی های محدب مجموع هر زاویۀ داخلی با زاویۀ خارجی متناظرش برابر است با \({180^ \circ }\)؛ مانند:
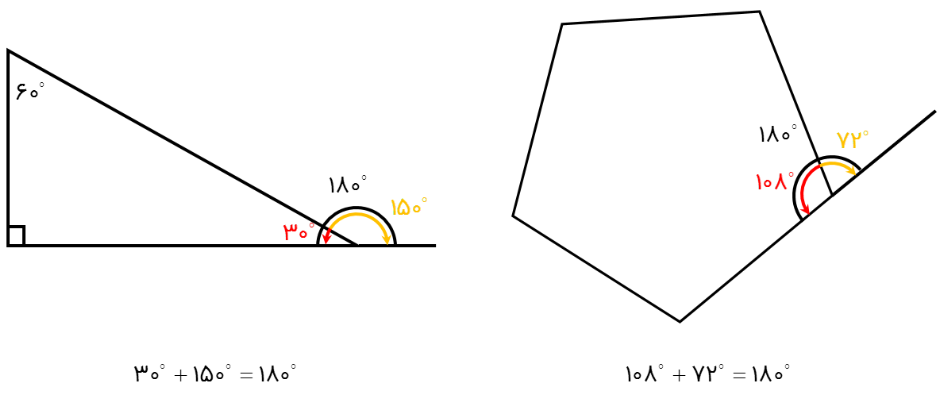
2 در چندضلعی های محدب، مجموع زاویه های خارجی \({360^ \circ }\) است؛ مانند:
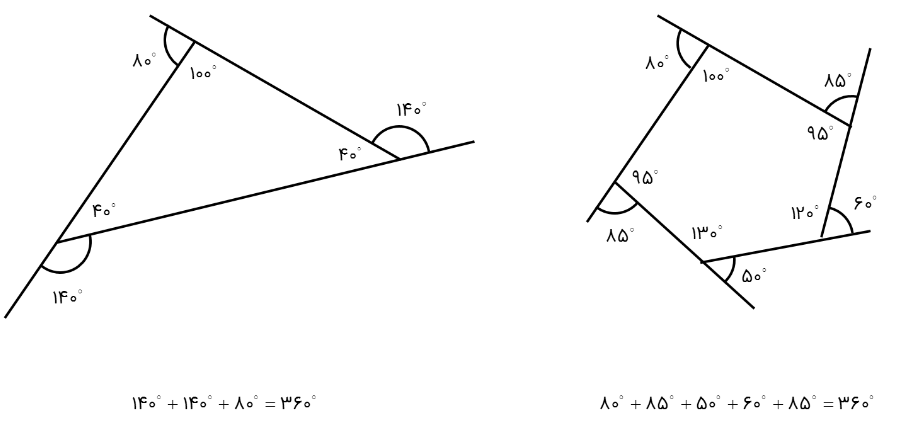
در شکل مقابل، اندازۀ x چند درجه است؟
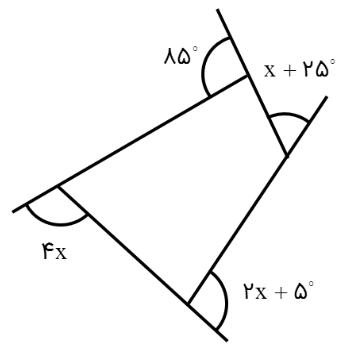
مجموع زاویه های خارجی در چندضلعی های محدب برابر است با 360 درجه:
\(\begin{array}{l}4x + (2x + {5^ \circ }) + (x + {25^ \circ }) + {85^ \circ } = {360^ \circ }\\\\ \Rightarrow 7x + {115^ \circ } = {360^ \circ } \Rightarrow 7x = {360^ \circ } - {115^ \circ } = {245^ \circ }\\\\ \Rightarrow x = \frac{{{{245}^ \circ }}}{7} = {35^ \circ }\end{array}\)
در چندضلعی های منتظم زاویه های خارجی برابرند، بنابراین برای بدست آوردن اندازۀ یک زاویۀ خارجی می توان \({360^ \circ }\) را بر تعداد زاویه های خارجی تقسیم کرد:
اندازۀ هر زاویۀ خارجی\( = \frac{{{{360}^ \circ }}}{n}\)
مثال
اندازۀ هر زاویۀ خارجی در ده ضلعی منتظم برابر است با: \({360^ \circ } \div 10 = {36^ \circ }\)
اگر اندازۀ یک زاویۀ داخلی n ضلعی منتظمی 156 درجه باشد، تعداد اضلاع چندضلعی را بیابید.
می دانیم مجموع هر زاویۀ خارجی با زاویۀ داخلی متناظرش برابر است با \({180^ \circ }\) . پس اندازۀ هر زاویۀ خارجی n ضلعی منتظم \({180^ \circ } - {156^ \circ } = {24^ \circ }\) . با توجه به اینکه می دانیم مجموع زاویه های خارجی باید \({360^ \circ }\) شود، بنابراین n ضلعی مورد نظر سؤال 15 ضلعی منتظم است:
\({360^ \circ } \div {24^ \circ } = 15\)
در هر مثلث، اندازۀ هر زاویۀ خارجی با مجموع دو زاویۀ داخلی غیر مجاورش (دو زاویۀ داخلی که کنارش قرار ندارند) برابر است.
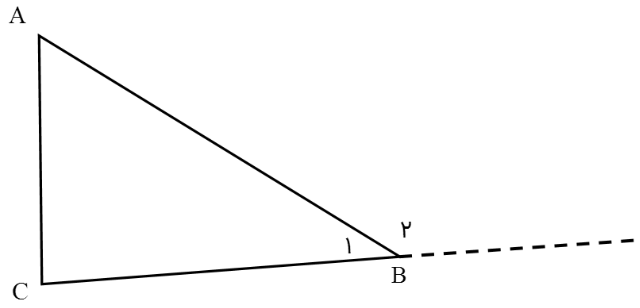
\(\left. \begin{array}{l}\hat A + {{\hat B}_1} + \hat C = {180^ \circ }\\\\{{\hat B}_1} + {{\hat B}_2} = {180^ \circ }\end{array} \right\} \Rightarrow {\hat B_2} = \hat A + \hat C\)
در شکل مقابل زاویۀ x چند درجه است؟
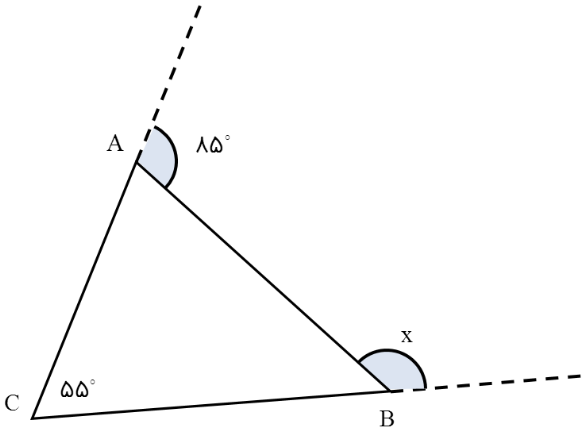
ابتدا زاویۀ داخلی A را به دست می آوریم:
\({180^ \circ } - {85^ \circ } = {95^ \circ }\)
حال با استفاده از نکتۀ قبل زاویۀ x را تعیین می کنیم:
\(x = {95^ \circ } + {55^ \circ } = {150^ \circ }\)
هرگاه روی محیط یک چندضلعی محدب حرکت کنیم به اندازۀ زاویه های خارجی شکل می چرخیم، یعنی \({360^ \circ }\).
مثال
لاک پشتی برای پیمودن محیط 5 ضلعی منتظم از نقطۀ A شروع می کند. وقتی می خواهد از روی ضلع AB روی ضلع BC قرار بگیرد به اندازۀ زاویۀ خارجی B می چرخد و بعد به اندازۀ زاویۀ خارجی C و ... . پس تا وقتی دوباره به نقطۀ A برگردد روی هم \({360^ \circ }\) می چرخد.
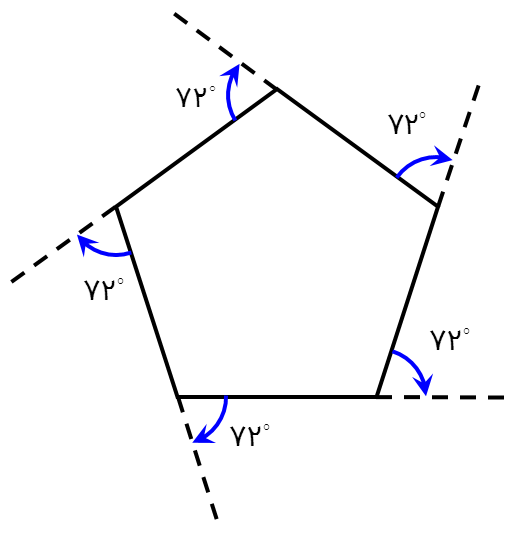
\(5 \times {72^ \circ } = {360^ \circ }\)
تهیه کننده: افسانه پهلیانی
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه هشتم- آزمون آنلاین تمامی دروس پایه هشتم
- گام به گام تمامی دروس پایه هشتم
- ویدئو های آموزشی تمامی دروس پایه هشتم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه هشتم
- فلش کارت های آماده دروس پایه هشتم
- گنجینه ای جامع از انشاء های آماده پایه هشتم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه هشتم



1736019749.png)















