1736019749.png)
جواب کاردرکلاس صفحه 57 درس 3 ریاضی دوازدهم تجربی (حد بی نهایت و حد در بی نهایت)
تعداد بازدید : 78.77Mپاسخ کاردرکلاس صفحه 57 ریاضی دوازدهم تجربی
-گام به گام کاردرکلاس صفحه 57 درس حد بی نهایت و حد در بی نهایت
-کاردرکلاس صفحه 57 درس 3
-شما در حال مشاهده جواب کاردرکلاس صفحه 57 ریاضی دوازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
1 حدود زیر را محاسبه کنید.
الف \(\mathop {\lim }\limits_{x \to {5^ - }} \;\frac{{2x}}{{x - 5}}\)
ب \(\mathop {\lim }\limits_{x \to {5^ + }} \;\frac{{2x}}{{x - 5}}\)
پ \(\mathop {\lim }\limits_{x \to 0} \;\frac{{ - 1}}{{{x^2}}}\)
ت \(\mathop {\lim }\limits_{x \to 3} \;\frac{2}{{\left| {x - 3} \right|}}\)
ث \(\mathop {\lim }\limits_{x \to - \frac{1}{3}} \;\frac{{\left[ x \right]}}{{\left| {3x + 1} \right|}}\)
ج \(\mathop {\lim }\limits_{x \to 0} \;\frac{{x + 1}}{{si{n^2}x}}\)
الف \(\mathop {\lim }\limits_{x \to {5^ - }} \;\frac{{2x}}{{x - 5}}\)
\(\mathop {\lim }\limits_{x \to {5^ - }} \;\frac{{2x}}{{x - 5}} = \frac{{2 \times 5}}{{{0^ - }}} = \frac{{10}}{{{0^ - }}} = - \;\infty \)
ب \(\mathop {\lim }\limits_{x \to {5^ + }} \;\frac{{2x}}{{x - 5}}\)
\(\mathop {\lim }\limits_{x \to {5^ + }} \;\frac{{2x}}{{x - 5}} = \frac{{2 \times 5}}{{{0^ + }}} = \frac{{10}}{{{0^ + }}} = + \;\infty \)
پ \(\mathop {\lim }\limits_{x \to 0} \;\frac{{ - 1}}{{{x^2}}}\)
\(\mathop {\lim }\limits_{x \to 0} \;\frac{{ - 1}}{{{x^2}}} = \frac{{ - 1}}{{{0^ + }}} = - \;\infty \)
ت \(\mathop {\lim }\limits_{x \to 3} \;\frac{2}{{\left| {x - 3} \right|}}\)
\(\mathop {\lim }\limits_{x \to 3} \;\frac{2}{{\left| {x - 3} \right|}} = \frac{2}{{{0^ + }}} = + \;\infty \)
ث \(\mathop {\lim }\limits_{x \to - \frac{1}{3}} \;\frac{{\left[ x \right]}}{{\left| {3x + 1} \right|}}\)
\(\mathop {\lim }\limits_{x \to - \frac{1}{3}} \;\frac{{\left[ x \right]}}{{\left| {3x + 1} \right|}} = \frac{{[ - \frac{1}{3}]}}{{{0^ + }}} = \frac{{ - 1}}{{{0^ + }}} = - \;\infty \)
ج \(\mathop {\lim }\limits_{x \to 0} \;\frac{{x + 1}}{{si{n^2}x}}\)
\(\mathop {\lim }\limits_{x \to 0} \;\frac{{x + 1}}{{si{n^2}x}} = \frac{1}{{{0^ + }}} = + \;\infty \)
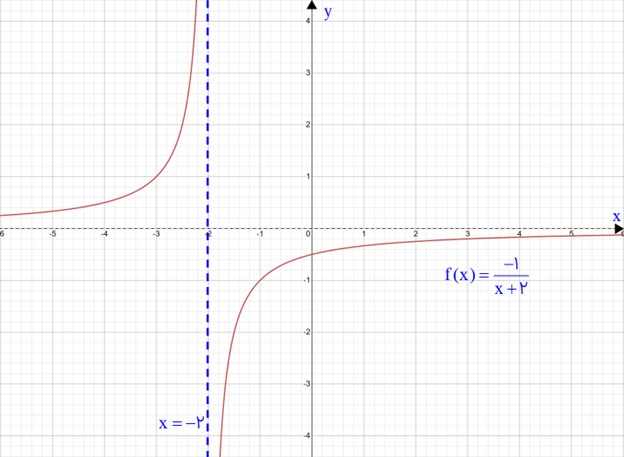
2 نمودار تابعی مانند f را رسم کنید که در یک همسایگی محذوف 2- تعریف شده باشد به طوری که \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right) = - \infty \) و \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} f\left( x \right) = + \infty \). پاسخ خود را با جواب های دوستانتان مقایسه کنید.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
