جواب کار در کلاس صفحه 18 درس 1 هندسه دوازدهم (ماتریس و کاربردها)
تعداد بازدید : 84.75Mپاسخ کار در کلاس صفحه 18 هندسه دوازدهم
-گام به گام کار در کلاس صفحه 18 درس ماتریس و کاربردها
-کار در کلاس صفحه 18 درس 1
-شما در حال مشاهده جواب کار در کلاس صفحه 18 هندسه دوازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 برای هر حالت B×A و A×B را در صورت امکان محاسبه کنید.
الف
\(\begin{array}{l}\left\{ \begin{array}{l}A = {\left[ {\begin{array}{*{20}{c}}1&{ - 1}&4\\0&0&0\\1&2&3\end{array}} \right]_{\;3 \times 3}}\\\\B = {\left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}1&2&3&{ - 1}\end{array}}\\{\begin{array}{*{20}{c}}{ - 1}&0&1&{ - 2}\end{array}}\\{\begin{array}{*{20}{c}}3&1&{ - 1}&0\end{array}}\end{array}} \right]_{\;3 \times 4}}\;\end{array} \right.\\\\ \Rightarrow \;A \times B = ...\end{array}\)
ب
\(\begin{array}{l}\left\{ \begin{array}{l}A = {\left[ {\begin{array}{*{20}{c}}1&{ - 1}\\{\begin{array}{*{20}{c}}2\\3\end{array}}&{\begin{array}{*{20}{c}}1\\{ - 2}\end{array}}\end{array}} \right]_{\;3 \times 2}}\\\\B = {\left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}2\\3\end{array}}&{\begin{array}{*{20}{c}}{ - 1}\\0\end{array}}&{\begin{array}{*{20}{c}}1\\5\end{array}}\end{array}} \right]_{\;2 \times 3}}\end{array} \right.\;\\\\ \Rightarrow \;A \times B = ...\;,\;B \times A = ...\end{array}\)
پ
\(\begin{array}{l}\left\{ \begin{array}{l}A = {\left[ \begin{array}{l}1\\ - 1\\2\end{array} \right]_{\;3 \times 1}}\\\\B = {\left[ {\begin{array}{*{20}{c}}2&3&4\end{array}} \right]_{\;1 \times 3}}\;\end{array} \right.\\\\ \Rightarrow \;A \times B = ...\;\;,\;\;B \times A = ...\end{array}\)
ت
\(\begin{array}{l}\left\{ \begin{array}{l}A = {\left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}1&{ - 1}\end{array}}&0\\{\begin{array}{*{20}{c}}2&{ - 1}\end{array}}&{ - 1}\end{array}} \right]_{\;2 \times 3}}\\\\B = {\left[ {\begin{array}{*{20}{c}}{ - 1}&2&{ - 2}\\{ - 1}&2&{ - 2}\\{ - 1}&2&{ - 2}\end{array}} \right]_{\;3 \times 3}}\end{array} \right.\\\\A \times B = \left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}0\\{...}\end{array}}&{\begin{array}{*{20}{c}}{...}\\{...}\end{array}}\end{array}}&{\begin{array}{*{20}{c}}{...}\\{...}\end{array}}\end{array}} \right]\end{array}\)
قسمت ت را با این حکم در اعداد حقیقی، که «اگر 0=b×a آنگاه a=0 یا b=0» مقایسه کنید.
الف
\(\begin{array}{l}\left\{ \begin{array}{l}A = {\left[ {\begin{array}{*{20}{c}}1&{ - 1}&4\\0&0&0\\1&2&3\end{array}} \right]_{\;3 \times 3}}\\\\B = {\left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}1&2&3&{ - 1}\end{array}}\\{\begin{array}{*{20}{c}}{ - 1}&0&1&{ - 2}\end{array}}\\{\begin{array}{*{20}{c}}3&1&{ - 1}&0\end{array}}\end{array}} \right]_{\;3 \times 4}}\;\end{array} \right.\;\\\\ \Rightarrow \;A \times B = \\\\\left[ {\begin{array}{*{20}{c}}1&{ - 1}&4\\0&0&0\\1&2&3\end{array}} \right] \times \left[ {\begin{array}{*{20}{c}}1&2&3&{ - 1}\\{ - 1}&0&1&{ - 2}\\3&1&{ - 1}&0\end{array}} \right] = \\\\\left[ {\begin{array}{*{20}{c}}{14}&6&{ - 2}&1\\0&0&0&0\\8&5&2&{ - 5}\end{array}} \right]\end{array}\)
ب
\(\begin{array}{l}\left\{ \begin{array}{l}A = {\left[ {\begin{array}{*{20}{c}}1&{ - 1}\\{\begin{array}{*{20}{c}}2\\3\end{array}}&{\begin{array}{*{20}{c}}1\\{ - 2}\end{array}}\end{array}} \right]_{\;3 \times 2}}\\\\B = {\left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}2\\3\end{array}}&{\begin{array}{*{20}{c}}{ - 1}\\0\end{array}}&{\begin{array}{*{20}{c}}1\\5\end{array}}\end{array}} \right]_{\;2 \times 3}}\end{array} \right.\;\;\\\\ \Rightarrow \;A \times B = \\\\\left[ {\begin{array}{*{20}{c}}1&{ - 1}\\2&1\\3&{ - 2}\end{array}} \right] \times \left[ {\begin{array}{*{20}{c}}2&{ - 1}&1\\3&0&5\end{array}} \right] = \\\\\left[ {\begin{array}{*{20}{c}}{ - 1}&{ - 1}&{ - 4}\\7&{ - 2}&7\\0&{ - 3}&{ - 7}\end{array}} \right]\\\\B \times A = \\\\\left[ {\begin{array}{*{20}{c}}2&{ - 1}&1\\3&0&5\end{array}} \right] \times \left[ {\begin{array}{*{20}{c}}1&{ - 1}\\2&1\\3&{ - 2}\end{array}} \right] = \\\\\left[ {\begin{array}{*{20}{c}}3&{ - 5}\\{18}&{ - 13}\end{array}} \right]\end{array}\)
پ
\(\begin{array}{l}\left\{ \begin{array}{l}A = {\left[ \begin{array}{l}1\\ - 1\\2\end{array} \right]_{\;3 \times 1}}\\\\B = {\left[ {\begin{array}{*{20}{c}}2&3&4\end{array}} \right]_{\;1 \times 3}}\;\end{array} \right.\\\\ \Rightarrow \;A \times B = \\\\\left[ {\begin{array}{*{20}{c}}1\\{ - 1}\\2\end{array}} \right] \times \left[ {\begin{array}{*{20}{c}}2&3&4\end{array}} \right] = \\\\\left[ {\begin{array}{*{20}{c}}3&3&4\\{ - 2}&{ - 3}&{ - 4}\\4&6&8\end{array}} \right]\\\\B \times A = \\\\\left[ {\begin{array}{*{20}{c}}2&3&4\end{array}} \right] \times \left[ {\begin{array}{*{20}{c}}1\\{ - 1}\\2\end{array}} \right] = \left[ 7 \right] = 7\end{array}\)
ت
\(\begin{array}{l}\left\{ \begin{array}{l}A = {\left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}1&{ - 1}\end{array}}&0\\{\begin{array}{*{20}{c}}2&{ - 1}\end{array}}&{ - 1}\end{array}} \right]_{\;2 \times 3}}\\\\B = {\left[ {\begin{array}{*{20}{c}}{ - 1}&2&{ - 2}\\{ - 1}&2&{ - 2}\\{ - 1}&2&{ - 2}\end{array}} \right]_{\;3 \times 3}}\end{array} \right.\\\\A \times B = \left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}0\\0\end{array}}&{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}}&{\begin{array}{*{20}{c}}0\\0\end{array}}\end{array}} \right]\end{array}\)
چنین حکمی در مورد قسمت (ت) صدق نمی کند؛ زیرا همان طور که می بینیم هیچ کدام از ماتریس ها A و B برابر با ماتریس ¯¯¯¯O نمی باشد.
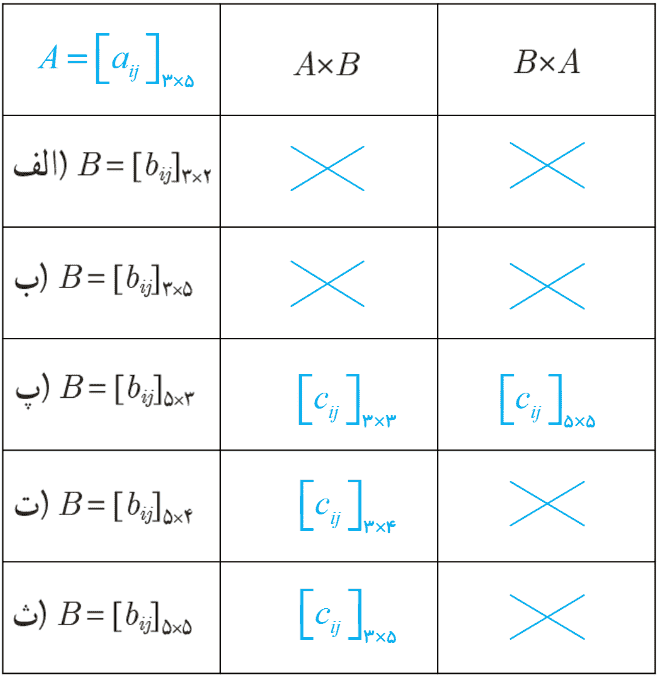
2 اگر A ماتریس 5×3 باشد در این صورت در هریک از حالت های زیر مشخص کنید که B×A و A×B قابل تعریف است یا خیر و در صورت تعریف مرتبهٔ آن را بیابی:
الف \(B = {\left[ {{b_{ij}}} \right]_{\;3 \times 2}}\)
ب \(B = {\left[ {{b_{ij}}} \right]_{\;3 \times 5}}\)
پ \(B = {\left[ {{b_{ij}}} \right]_{\;5 \times 3}}\)
ت \(B = {\left[ {{b_{ij}}} \right]_{\;5 \times 4}}\)
ث \(B = {\left[ {{b_{ij}}} \right]_{\;5 \times 5}}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















