گام به گام مرور فصل 7 صفحه 118 درس 7 ریاضی هشتم (توان و جذر)

1 توان:

یعنی پایه را به تعداد عدد توان در خودش ضرب کنیم.

\({3^4} = 3 \times 3 \times 3 \times 3\)

2 جذر تقریبی:

تقریب زدن جذر یک عدد که جذر کاملی ندارد.

\(\sqrt 3 = 1/732 \cdots \simeq 1/73\)

3 ریشه های دوم یک عدد:

مقادیر مثبت و منفی جذر یک عدد.

\(\sqrt 4 = 2\;,\; - 2\)

4 جذر حاصل ضرب و حاصل تقسیم:

جذر حاصل ضرب برابر حاصل ضرب جذر هر کدام از آنها:

\(\sqrt {4 \times 25} = \sqrt 4 \times \sqrt {25} = 2 \times 5 = 10\)

و جذر حاصل تقسیم برابر حاصل تقسیم جذر هر کدام از آنها:

\(\sqrt {\frac{{36}}{{16}}} = \frac{{\sqrt {36} }}{{\sqrt {16} }} = \frac{6}{4} = 1/5\)

1 محاسبهٔ حاصل یک عدد توان دار به توان عدد دیگر:

پایه را می نویسیم و توان ها را در هم ضرب می کنیم.

\({({2^3})^4} = {2^{3 \times 4}} = {2^{12}}\)

2 محاسبهٔ تقسیم دو عدد توان دار با پایه های مساوی:

پایه را می نویسیم و توان ها را از هم کم می کنیم.

\(\frac{{{3^4}}}{{{3^2}}} = {3^{4 - 2}} = {3^2}\)

3 محاسبهٔ تقریبی تقسیم دو عدد توان دار با نماهای مساوی:

پایه ها را بر هم تقسیم می کنیم و توان را می نویسیم.

\(\frac{{{3^4}}}{{{2^4}}} = {(\frac{3}{2})^4} = \frac{{81}}{{16}} \simeq 5/06\)

4 محاسبهٔ جذر یک عدد:

ابتدا بررسی می کنیم ببینیم که عددی که می خواهیم از آن جذر بگیریم، بین کدام دو عدد دارای مربع کامل است.

\(\begin{array}{l}\sqrt x = ?\\\\{m^2} < x < {n^2}\\\\m < \sqrt x < n\end{array}\)

بعد از آن، جذر اعداد مربع کامل را می گیریم. میانگین دو عدد بدست آمده را محاسبه می کنیم و مربع آن را بدست می آوریم.

\(\frac{{m + n}}{2} \to {(\frac{{m + n}}{2})^2}\)

حال بررسی می کنیم که آیا عددی که می خواهیم از آن جذر بگیریم، از این عدد کوچکتر بود، جذر عدد مورد نظر ما بین عدد با مربع کوچکتر  و میانگین دو عدد قرار دارد.

\(\begin{array}{l}{m^2} < x < {(\frac{{m + n}}{2})^2}\\\\m < \sqrt x < \frac{{m + n}}{2}\end{array}\)

حال این اعداد با رقم اول اعشار بین این دو عدد را در یک جدول نوشته و توان دوم آن ها را بدست می آوریم. آن عددی که کوچکتر و نزدیکتر به عددی که جذر آن را می خواهیم بگیریم، باشد، جواب مسئله می باشد.

اگر جذر عدد مورد نظر ما بین میانگین دو عدد و عدد با مربع کوچکتر قرار داشته باشد، یعنی:

\(\begin{array}{l}{(\frac{{m + n}}{2})^2} < x < {n^2}\\\\\frac{{m + n}}{2} < \sqrt x < n\end{array}\)

در این صورت مثل کاری که در بالا توضیح دادیم، این بار بین دو عدد مورد نظر انجام می دیم. آن عددی که کوچکتر و نزدیکتر به عددی که جذر آن را می خواهیم بگیریم، باشد، جواب مسئله می باشد.

با دو مثال، این روش را توضیح می دهیم؛ ابتدا جذر عددی را به دست می آوریم که از میانگین جذر دو عدد مربع کامل کمتر باشد:

\(\begin{array}{l}\sqrt {41} = ?\\\\36 < 41 < 49\\\\6 < \sqrt {41} < 7\\\\\frac{{6 + 7}}{2} = 6/5\\\\{(6/5)^2} = 42/25 \Rightarrow 41 < 42/25\\\\6 < \sqrt {41} < 6/5\end{array}\)

همانطور که می بینیم عدد 6/4 نزدیکترین عدد به جذر عدد 41 می باشد؛ زیرا که توان دوم آن به عدد 41 نزدیکتر است نسبت به باقی اعداد ردیف مجذور:

\(\sqrt {41} = 6/4\)

حال جذر عددی را به دست می آوریم که از میانگین جذر دو عدد مربع کامل بیشتر باشد:

\(\begin{array}{l}\sqrt {47} = ?\\\\36 < 47 < 49\\\\6 < \sqrt {47} < 7\\\\\frac{{6 + 7}}{2} = 6/5\\\\{(6/5)^2} = 42/25 \Rightarrow 47 > 42/25\\\\6/5 < \sqrt {47} < 7\end{array}\)

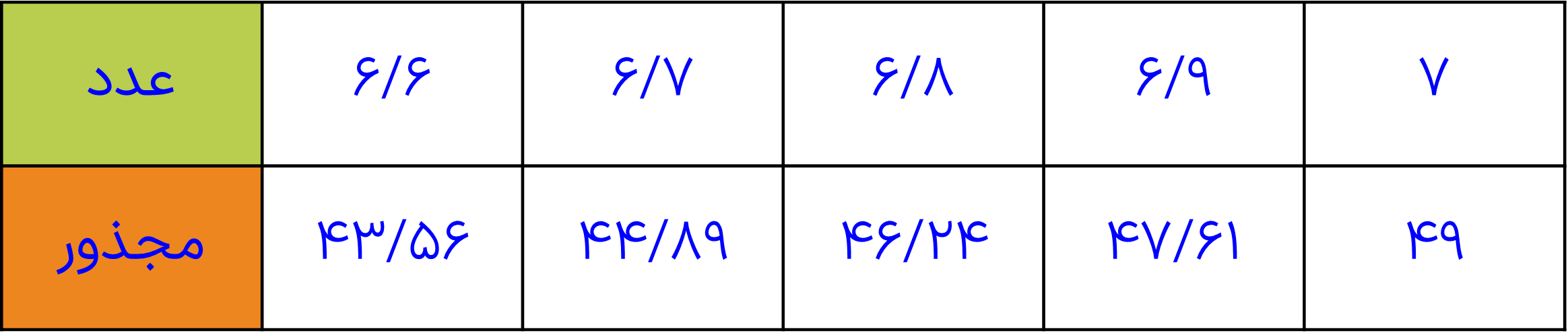
این روش برای اینکه جذر اعداد را تا یک رقم اعشار بدست آوریم. اگر بخواهیم تا دو رقم اعشار آن را بدست آوریم، کافی است که میانگین عدد بدست آمده و عدد اعشاری بعدی بزرگتر از این عدد را بدست آوریم و به روشی که در بالا توضیح دادیم، جذر عدد مورد نظر را تا دو رقم اعشار بدست آوریم. برای بدست آوردن رقم های بعدی اعشار نیز همین کار را می توانیم ادامه دهیم.

5 محاسبهٔ یک عبارت توان دار:

ابتدا عبارت هایی که پایه های یکسان دارند را ساده می کنیم، سپس عدد هایی که توان یکسان دارند را با هم ساده می کنیم.

\(\begin{array}{l}\frac{{{3^4} \times {4^7}}}{{{2^6} \times {9^4}}} = \frac{{{3^4} \times {4^7}}}{{{{({2^2})}^3} \times {{({3^2})}^4}}} = \frac{{{3^4} \times {4^7}}}{{{4^3} \times {3^8}}} = \\\\\frac{{{4^4}}}{{{3^4}}} = \frac{{256}}{{81}} \simeq 3/16\end{array}\)

6 ساده کردن یک عبارت توان دار:

ابتدا عبارت هایی که پایه های یکسان دارند راساده می کنیم، سپس عدد هایی که توان یکسان دارند را با هم ساده می کنیم.

\(\begin{array}{l}\frac{{{3^4} \times {4^7}}}{{{2^6} \times {9^4}}} = \frac{{{3^4} \times {4^7}}}{{{{({2^2})}^3} \times {{({3^2})}^4}}} = \frac{{{3^4} \times {4^7}}}{{{4^3} \times {3^8}}} = \\\\\frac{{{4^4}}}{{{3^4}}} = {(\frac{4}{3})^4}\end{array}\)

7 پیدا کردن عددهای رادیکالی روی محور:

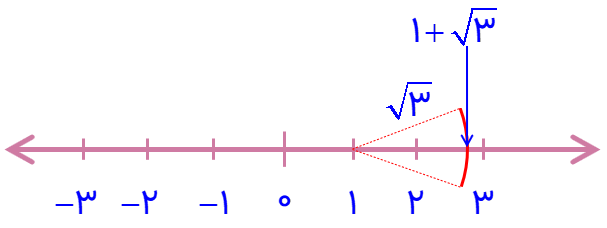
ابتدا اندازه دو سر پرگار را به اندازه عدد رادیکالی باز می کنیم. سپس سر پرگار را روی عدد صحیح می گذاریم  و یک کمان روی محور اعداد می زنیم . نقطه ای که از تقاطع کمان و محور بدست می آید همان عدد رادیکالی است. به عنوان مثال می خواهیم عدد \(1 + \sqrt 3 \) را پیدا کنیم. ابتدا اندازه دو سر پرگار را به اندازه عدد \(\sqrt 3 \) باز می کنیم. سپس سر پرگار را روی عدد 1 می گذاریم  و یک کمان روی محور اعداد مطابق شکل زیر می زنیم.

8 محاسبهٔ جذر حاصل ضرب و حاصل تقسیم:

جذر حاصل ضرب برابر حاصل ضرب جذر هر کدام از آنها:

\(\begin{array}{l}\sqrt {169 \times 144} = \sqrt {169} \times \sqrt {144} = \\\\13 \times 12 = 156\end{array}\)

و جذر حاصل تقسیم برابر حاصل تقسیم جذر هر کدام از آنها:

\(\sqrt {\frac{{25}}{{16}}} = \frac{{\sqrt {25} }}{{\sqrt {16} }} = \frac{5}{4} = 1/25\)

\(\begin{array}{l}\frac{{{{( - 3)}^5} \times {2^4} \times 8}}{{ - {2^7} \times {{( - 9)}^2} \times 18}} = \frac{{ - {3^5} \times {2^4} \times {2^3}}}{{ - {2^7} \times {3^4} \times 2 \times {3^2}}} = \\\\\frac{{ - {3^5} \times {2^7}}}{{ - {3^6} \times {2^8}}} = \frac{1}{{3 \times 2}} = \frac{1}{6}\end{array}\)

\(\begin{array}{l}{\left[ {{3^{10}} \times {{(\frac{1}{{27}})}^3}} \right]^2} \div {\left[ {{5^4} \times {{(\frac{1}{{25}})}^2}} \right]^3} = \\\\{\left[ {{3^{10}} \times {{(\frac{1}{{{3^3}}})}^3}} \right]^2} \div {\left[ {{5^4} \times {{(\frac{1}{{{5^2}}})}^2}} \right]^3} = \\\\{\left[ {{3^{10}} \times \frac{1}{{{3^9}}}} \right]^2} \div {\left[ {{5^4} \times \frac{1}{{{5^4}}}} \right]^3} = \\\\{\left[ 3 \right]^2} \div {\left[ 1 \right]^3} = 9 \div 1 = 9\end{array}\)

\(\begin{array}{l}81 < 93 < 100\\\\9 < \sqrt {93} < 10\\\\ \Rightarrow \frac{{9 + 10}}{2} = 9/5\\\\ \Rightarrow 9/5 \times 9/5 = 90/25\end{array}\)

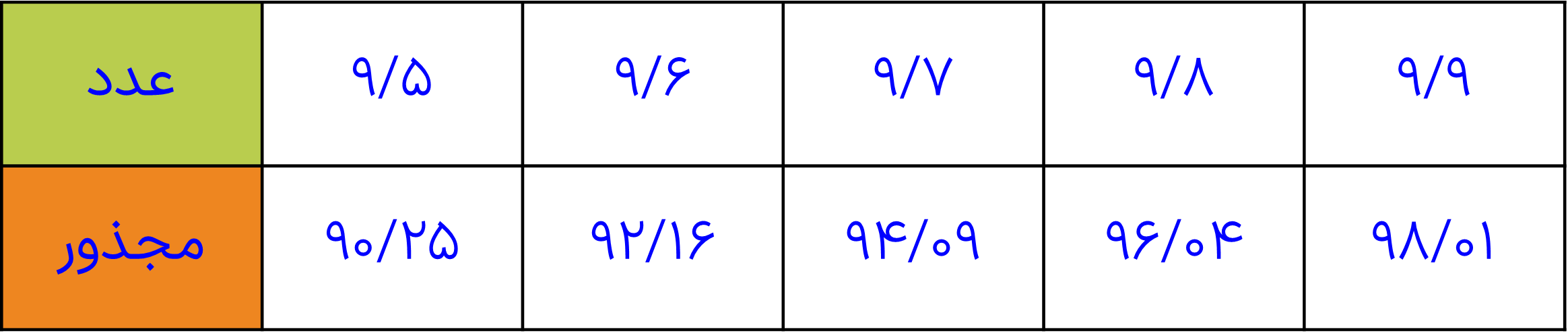
\(\begin{array}{l} \Rightarrow 9/6 < \sqrt {93} < 9/7\\\\ \Rightarrow \frac{{9/6 + 9/7}}{2} = 9/65\\\\ \Rightarrow 9/65 \times 9/65 = 93/12\end{array}\)

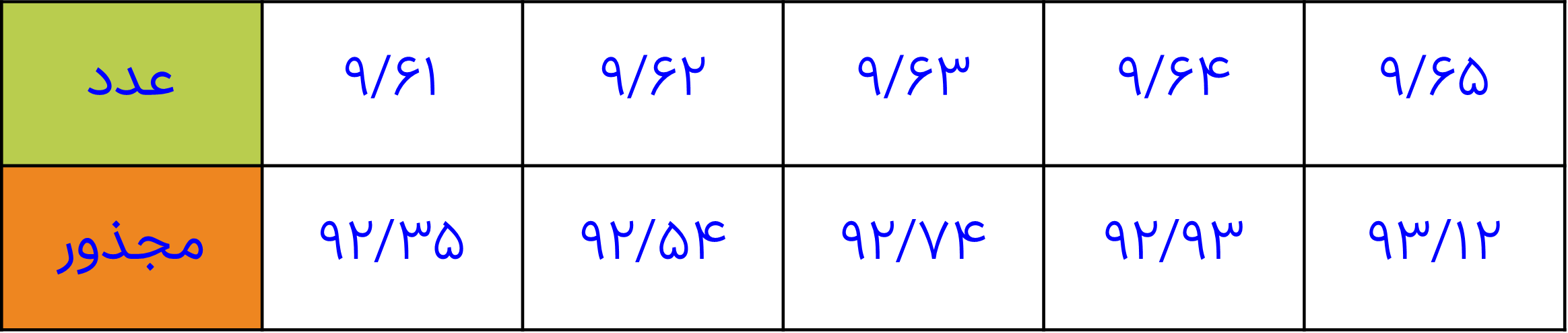
طبق جداول، جذر عدد 93 تا دو رقم اعشار برابر 9/64 می باشد.

\(\begin{array}{l} - {2^4} < \sqrt {25} < 6 < \sqrt {47} < {2^3} < {( - 2)^4} < {( - 2/5)^4}\\\\ - {2^4}\,,\,\sqrt {25} \,,\,6\,,\,\sqrt {47} \,,\,{2^3}\,,\,{( - 2)^4}\,,\,{( - 2/5)^4}\end{array}\)

\(\sqrt {10} \)

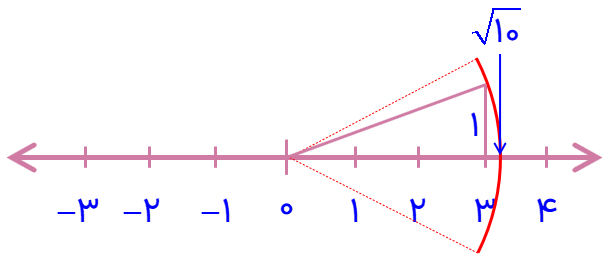
\(\sqrt {13} \)

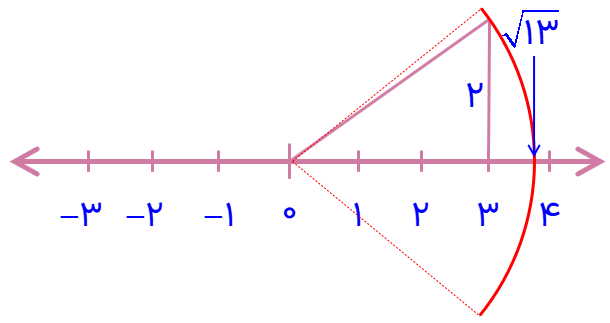
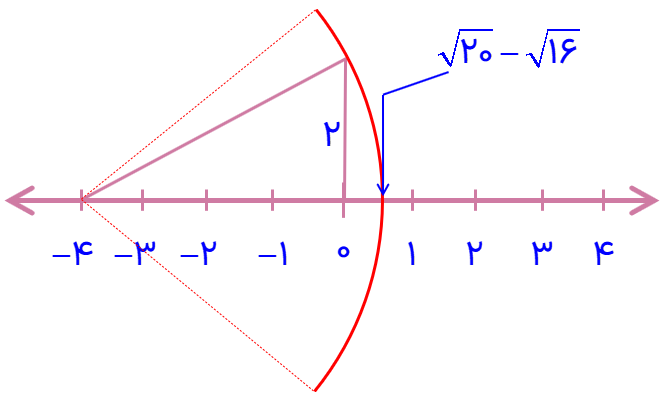
\(\sqrt {20} - \sqrt {16} = - \sqrt {16} + \sqrt {20} = - 4 + \sqrt {20} \)