جواب تمرین صفحه 117 درس 7 ریاضی هشتم (توان و جذر)
تعداد بازدید : 80.71Mپاسخ تمرین صفحه 117 ریاضی هشتم
-گام به گام تمرین صفحه 117 درس توان و جذر
-تمرین صفحه 117 درس 7
-شما در حال مشاهده جواب تمرین صفحه 117 ریاضی هشتم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 نزدیک ترین عدد طبیعی به هر یک از عددهای زیر را پیدا کنید.
\(\begin{array}{l}\sqrt {401} \\\\\sqrt {310} \\\\\sqrt {9999} \\\\\sqrt {280} \\\\\sqrt {175} \end{array}\)
درستی پاسخ خود را به کمک ماشین حساب بیازمایید.
\(\begin{array}{l}\sqrt {401} \to \sqrt {400} = 20\\\\\sqrt {310} \to \sqrt {324} = 18\\\\\sqrt {9999} \to \sqrt {10000} = 100\\\\\sqrt {280} \to \sqrt {289} = 17\\\\\sqrt {175} \to \sqrt {169} = 13\end{array}\)
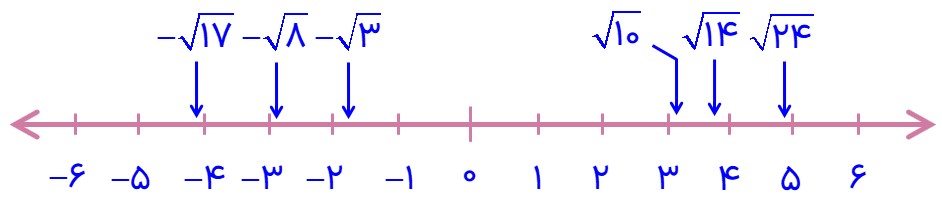
2 یک محور اعداد رسم کنید و عددهای زیر را به صورت تقریبی روی آن مشخص کنید.
\(\sqrt {14} \;,\;\sqrt {10} \;,\;\sqrt {24} \;,\; - \sqrt 3 \;,\; - \sqrt 8 \;,\; - \sqrt {17} \)
3 مجموع عددهای واقع بر هر سطر، هر ستون و نیز هر قطر مربع زیر 6- است.
جاهای خالی را با چه عددهایی می توان پر کرد؟


4 حاصل هر یک از عبارت های زیر را به دست آورید.
\(\begin{array}{l}({a^5} \times {a^9}) \times ({b^{17}} \div {b^3}) = \\\\\sqrt {\frac{{49 \times 25}}{{36}}} = \end{array}\)
\(\begin{array}{l}({a^5} \times {a^9}) \times ({b^{17}} \div {b^3}) = {a^{14}} \times {b^{14}} = {(ab)^{14}}\\\\\sqrt {\frac{{49 \times 25}}{{36}}} = \frac{{\sqrt {49} \times \sqrt {25} }}{{\sqrt {36} }} = \frac{{7 \times 5}}{6} = \frac{{35}}{6}\end{array}\)
5 جذر 700 را تا یک رقم اعشار به دست آورید و نتیجه را به کمک ماشین حساب بررسی کنید.
\(\begin{array}{l}\sqrt {676} < \sqrt {700} < \sqrt {729} \\\\26 < \sqrt {700} < 27\\\\\frac{{26 + 27}}{2} = 26/5\\\\26/5 \times 26/5 = 702/25\end{array}\)

\(\sqrt {700} = 26/4\)
مقدار جذر 700 را با ماشین حساب بدست می آوریم:
\(\sqrt {700} = 26/4575 \cdots \)
نتیجه بررسی این است که مقدار جذر 700 تا یک رقم اعشار برابر 26/4 می باشد.
6 دو عدد طبیعی بین \(\sqrt 5 \) و \(\sqrt {17} \) پیدا کنید.
\(\sqrt 5 \;,\;\sqrt 9 \;,\;\sqrt {16} \;,\;\sqrt {17} \to \sqrt 5 \;,\;3\;,\;4\;,\;\sqrt {17} \)
دو عدد طبیعی 3 و 4 می باشند.
7 پنج عدد بین \(\sqrt 3 \) و \(\sqrt 8 \) پیدا کنید.
بی نهایت عدد می توان بین \(\sqrt 3 \) و \(\sqrt 8 \) پیدا کرد که 5 تا از این اعداد را در زیر آورده ایم:
\(\begin{array}{l}\sqrt 3 < 2 < \sqrt 5 < \sqrt 6 < \sqrt 7 < \sqrt {7/5} < \sqrt 8 \\\\ \to 2\;,\;\sqrt 5 \;,\;\sqrt 6 \;,\;\sqrt 7 \;,\;\sqrt {7/5} \end{array}\)
8 اعداد رادیکالی زیر را به صورت ضرب یک عدد طبیعی در یک رادیکال بنویسید.
\(\begin{array}{l}\sqrt {27} \\\\\sqrt {50} \\\\\sqrt {200} \end{array}\)
\(\begin{array}{l}\sqrt {27} = \sqrt 9 \times \sqrt 3 = 3\sqrt 3 \\\\\sqrt {50} = \sqrt {25} \times \sqrt 2 = 5\sqrt 2 \\\\\sqrt {200} = \sqrt {100} \times \sqrt 2 = 10\sqrt 2 \end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















