جواب فصل 4 معادله ها و نامعادله ها ریاضی دهم
تعداد بازدید : 3.13Mپاسخ به تمامی سوالات فصل معادله ها و نامعادله ها - حل المسائل فصل 4 معادله ها و نامعادله ها - گام به گام 1401 کتاب ریاضی دهم - گام به گام کتاب ریاضی دهم مطابق با آخرین تغییرات کتب درسی
فعالیت صفحه 71 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ فعالیت صفحه 71 درس 4
جواب فعالیت صفحه 71 درس 4 ریاضی دهم
معادلهٔ درجه دوم \({x^2} - 2x - 3 = 0\) را که درسا در بخش قبل به آن رسید، درنظر بگیرید.
1 با تجزیهٔ سمت چپ معادلهٔ بالا، جای خالی را با عدد مناسب پر کنید.
\((x + 1) (x - ….) = 0\)
\((x + 1) (x – 3) = 0\)
2
الف از ویژگی بالا استفاده کنید و جاهای خالی را با عبارت های مناسب پر کنید.
\(\left( {x{\rm{ }} + {\rm{ }}1} \right){\rm{ }}\left( {x{\rm{ }} - {\rm{ }} \ldots .} \right){\rm{ }} = {\rm{ }}0 \to x{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}0\) یا \(x{\rm{ }} - {\rm{ }} \ldots .{\rm{ }} = {\rm{ }}0\; \to x{\rm{ }} = {\rm{ }} - 1\;\) یا \(\;x{\rm{ }} = {\rm{ }} \ldots .\)
ب برای اطمینان از صحت جواب های حاصل شده، می توانیم هر دو جواب به دست آمده را در معادله قرار دهیم و آنها را آزمایش کنیم. یکی از جواب ها آزمایش شده است؛ جواب دیگر را آزمایش کنید.

پ آیا هر دو جواب این معادله می توانند طول اضلاع مثلث قائم الزاویه ای باشند که قبلا دربارهٔ آن بحث شده است؟ توضیح دهید.
الف
\(\left( {x{\rm{ }} + {\rm{ }}1} \right){\rm{ }}\left( {x{\rm{ }} - {\rm{ }}3} \right){\rm{ }} = {\rm{ }}0 \to x{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}0\) یا \(x{\rm{ }} - {\rm{ }}3{\rm{ }} = {\rm{ }}0\; \to \;x{\rm{ }} = {\rm{ }} - 1\) یا \(x = 3\)
ب
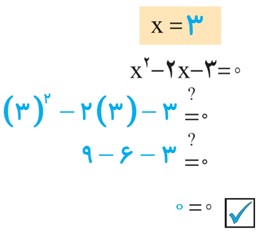
پ
خیر؛ زیرا یکی از مقادیر منفی است و فقط عدد 3 جواب مسأله می باشد.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
کاردرکلاس صفحه 71 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ کاردرکلاس صفحه 71 درس 4
جواب کاردرکلاس صفحه 71 درس 4 ریاضی دهم
معادله های درجهٔ دوم زیر را به روش تجزیه حل کنید و جواب های خود را آزمایش کنید.
الف \({x^2} - 3x = 10\)
ب \(3{t^2} - t = 0\)
الف
\(\begin{array}{*{20}{l}}{{x^2} - 3x - 10 = 0}\\{\left( {x - 5} \right)\left( {x + 2} \right) = 0}\\{x - 5 = 0}\\{ \Rightarrow x = 5 \to {{\left( 5 \right)}^2} - 3\left( 5 \right) - 10 = 0}\\{x + 2 = 0}\\{ \Rightarrow x = - 2 \to {{\left( { - 2} \right)}^2} - 3\left( { - 2} \right) - 10 = 0}\end{array}\)
ب
\(\begin{array}{*{20}{l}}{t\left( {3t - 1} \right) = 0}\\{t = 0 \to \left( 0 \right)\left( {3 \times 0 - 1} \right) = 0}\\{3t - 1 = 0 \Rightarrow t = \frac{1}{3} \to \left( {\frac{1}{3}} \right)\left( {3 \times \frac{1}{3} - 1} \right) = 0}\end{array}\)
گام به گام کتاب های پایه دهم
گام به گام جامع کتاب ریاضی دهم
گام به گام جامع کتاب شیمی دهم
گام به گام جامع کتاب فارسی دهم
گام به گام جامع کتاب نگارش دهم
گام به گام جامع کتاب عربی دهم
گام به گام جامع کتاب زبان انگلیسی دهم
گام به گام جامع کتاب کتاب کار انگلیسی دهم
گام به گام جامع کتاب آمادگی دفاعی دهم
گام به گام جامع کتاب دین و زندگی دهم
گام به گام جامع کتاب جغرافیای ایران دهم
گام به گام جامع کتاب آزمایشگاه علوم تجربی دهم
گام به گام جامع کتاب تفکر و سواد رسانه ای دهم
گام به گام جامع کتاب کارگاه کارآفرینی و تولید
فعالیت صفحه 72 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ فعالیت صفحه 72 درس 4
جواب فعالیت صفحه 72 درس 4 ریاضی دهم
معادلهٔ درجه دوم x2=25 را در نظر بگیرید.
1 جواب های این معادله را به روش تجزیه به دست آورید.
\(\begin{array}{*{20}{l}}{{x^2} = 25 \Rightarrow {x^2} - 25 = 0 \Rightarrow \left( {x - 5} \right)\left( {x + 5} \right) = 0}\\{x - 5 = 0 \Rightarrow x = 5}\\{x + 5 = 0 \Rightarrow x = - \:5}\end{array}\)
2 ریشه های دوم عدد ٢٥ را به دست آورید. این معادله را به روش تجزیه نیز حل کنید و جواب های به دست آمده را با این جواب ها مقایسه کنید.
روش تجزیه به صورت زیر است:
\(\begin{array}{*{20}{l}}{{x^2} = 25 \Rightarrow {x^2} - 25 = 0 \Rightarrow \left( {x - 5} \right)\left( {x + 5} \right) = 0}\\{x - 5 = 0 \Rightarrow x = 5}\\{x + 5 = 0 \Rightarrow x = - \:5}\end{array}\)
روش ریشه گرفتن نیز به صورت زیر است:
\(x = \sqrt {25} \Rightarrow {x^2} = 25 \Rightarrow x = \pm 5\)
نتیجه می گیریم که از هر یک از روش های بالا برویم ، جواب بدست آمده صحیح می باشد.
3 اگر x2=a یک معادلهٔ درجه دوم باشد که در آن a یک عدد حقیقی است، آیا همیشه می توان جواب های آن را به صورت \(x = \pm \sqrt a \) نوشت؟ توضیح دهید.
خیر؛ این معادله فقط برای اعداد نامنفی یعنی \(a \ge 0\) جواب دارد.
مثال صفحه 72 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ مثال صفحه 72 درس 4
جواب مثال صفحه 72 درس 4 ریاضی دهم
با یک دستگاه برش، یک صفحهٔ مقوایی به شکل مربع را برش می زنیم. سپس، چهار مربع کوچک در گوشه های آن را جدا می کنیم. بعد با تا زدن لبه ها، یک جعبه می سازیم. اگر مربع های جداشده به ضلع 2 سانتی متر باشند و بخواهیم حجم این جعبه، 200 سانتی متر مکعب باشد، طول اضلاع کاغذهایی را که باید برای این کار انتخاب شوند، به دست آورید.
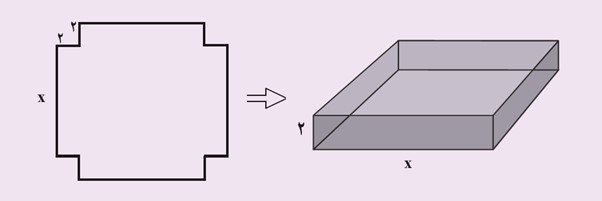
حل: از مقوایی که در شکل سمت چپ رسم شده، چهار مربع به ضلع 2 سانتی متر جدا می کنیم تا جعبه ای که سمت راست رسم شده، به دست آید. حجم این جعبه عبارت است از:
ارتفاع × عرض × طول = (x)(x)(2) = 2xx
الف از آنجا که حجم جعبه، 200 سانتی متر مکعب باید باشد، داریم: 2x2=200. بنابراین x2=..… و با محاسبهٔ ریشه های دوم این معادله، جواب های x=….. به دست می آید.
ب و چون طول نمی تواند منفی باشد، تنها x=….. مورد قبول است و طول ضلع مربع اولیه x+….=….+….=…. سانتی متر است.
الف
\(x = \pm 10\,\,\,\,\, - \,\,\,\,\,\,{x^2} = 100\)
ب
\(x + 4 = 10 + 4 = 14\,\,\,\,\,\,\, - \,\,\,\,\,\,x = \pm 10\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
کاردرکلاس صفحه 73 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ کاردرکلاس صفحه 73 درس 4
جواب کاردرکلاس صفحه 73 درس 4 ریاضی دهم
جواب هر یک از معادله های زیر را در صورت وجود به روش ریشه گیری به دست آورید.
الف \(5{x^2} = 20\)
ب \({t^2} + 7 = 0\)
پ \({\left( {r - 2} \right)^2} = 16\)
الف
\(\begin{array}{*{20}{l}}{{x^2} = 4}\\{x = 2}\\{x = - 2}\end{array}\)
ب
\(\begin{array}{*{20}{l}}{{t^2} = - 7}\\{t = \pm \sqrt { - 7} }\end{array}\)
جواب ندارد
پ
\(\begin{array}{*{20}{l}}{r - 2 = \pm 4}\\{r - 2 = 4 \to r = 6}\\{r - 2 = - 4 \to r = - 2}\end{array}\)
گام به گام کتاب های پایه دهم
گام به گام جامع کتاب ریاضی دهم
گام به گام جامع کتاب شیمی دهم
گام به گام جامع کتاب فارسی دهم
گام به گام جامع کتاب نگارش دهم
گام به گام جامع کتاب عربی دهم
گام به گام جامع کتاب زبان انگلیسی دهم
گام به گام جامع کتاب کتاب کار انگلیسی دهم
گام به گام جامع کتاب آمادگی دفاعی دهم
گام به گام جامع کتاب دین و زندگی دهم
گام به گام جامع کتاب جغرافیای ایران دهم
گام به گام جامع کتاب آزمایشگاه علوم تجربی دهم
گام به گام جامع کتاب تفکر و سواد رسانه ای دهم
گام به گام جامع کتاب کارگاه کارآفرینی و تولید
فعالیت صفحه 73 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ فعالیت صفحه 73 درس 4
جواب فعالیت صفحه 73 درس 4 ریاضی دهم
1 دو جمله ای\({x^2} + 6x\) را درنظر بگیرید. چه عددی باید به این دو جمله ای اضافه شود تا چند جمله ای حاصل به شکل مربع کامل نوشته شود؟ جاهای خالی را با اعداد مناسب پر کنید.
\({x^2} + 6x + \;... = {\left( {x + \;...} \right)^2}\)
اعدادی که در جاهای خالی نوشته اید ، چه ارتباطی با شکل روبه رو دارند؟
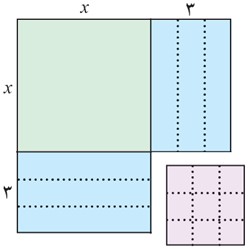
قطعه جدا شده در شکل 9 مربع دارد یعنی مربع عدد 3 ؛ در نتیجه عدد 3 را در پرانتز سمت راست تساوی و عدد 9 را در سمت چپ تساوی می گذاریم.
\({x^2} + 6x + 9 = {\left( {x + 3} \right)^2}\)
2 اگر a یک عدد حقیقی باشد، به دو جمله ای x2+ax چه جمله ای باید اضافه شود تا به شکل مربع کامل درآید؟ جاهای خالی را با عبارت های مناسب پر کنید.
\({x^2} + ax + \;... = {\left( {x + \;...} \right)^2}\)
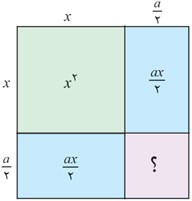
\({x^2} + ax + \frac{{{a^2}}}{4} = {(x + \frac{a}{2})^2}\)
مثال صفحه 73 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ مثال صفحه 73 درس 4
جواب مثال صفحه 73 درس 4 ریاضی دهم
معادلۀ \({x^2} - 6x + 4 = 0\) را به روش مربع کامل حل می کنیم.
\({x^2} - 6x + 4 = 0\) معادلهٔ درجه دوم
\({x^2} - 6x = - 4\) به دو طرف معادله، 4- را اضافه کرده ایم
\({x^2} - 6x + \;... = - 4 + ...\) به دو طرف معادله ....... را اضافه کرده ایم تا سمت چپ مربع کامل شود
سمت چپ را به شکل مربع کامل می نویسیم \({\left( {x - 3} \right)^2} = 5\)
\(x - 3 = \pm \sqrt 5 \) از دوطرف معادله، ریشهٔ دوم می گیریم
\(x = 3 \pm \sqrt 5 \) به دو طرف معادله عدد 3 را اضافه کرده ایم
بنابراین جواب ها یا ریشه های این معادله عبارت اند از \(x = 3 + \sqrt 5 \) و \(x = 3 - \sqrt 5 \)
به دو طرف معادله 9 را اضافه کرده ایم تا سمت چپ مربع کامل شود \({x^2} - 6x + \;9 = - 4 + 9\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
کاردرکلاس صفحه 74 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ کاردرکلاس صفحه 74 درس 4
جواب کاردرکلاس صفحه 74 درس 4 ریاضی دهم
معادله های زیر را به روش مربع کامل حل کنید.
الف \({x^2} + 2x = 24\)
ب \({t^2} + 3t = 3\)
پ \({n^2} - 4n + 5 = 0\)
ت \(2{r^2} + r - 2 = 0\)
الف
\(\begin{array}{*{20}{l}}{{x^2} + 2x + {{\left( {\frac{2}{2}} \right)}^2} = 24 + {{\left( {\frac{2}{2}} \right)}^2}}\\{{{\left( {x + 1} \right)}^2} = 25}\\{x + 1 = \pm 5}\\{x = 5 - 1 = 4}\\{x = - 5 - 1 = - 6}\end{array}\)
ب
\(\begin{array}{*{20}{l}}{{t^2} + 3t + {{\left( {\frac{3}{2}} \right)}^2} = 3 + {{\left( {\frac{3}{2}} \right)}^2}}\\{{{\left( {t + \frac{3}{2}} \right)}^2} = \frac{{45}}{4}}\\{t + \frac{3}{2} = \pm \frac{{3\sqrt 5 }}{2}}\\{t = - \frac{3}{2} + \frac{{3\sqrt 5 }}{2}}\\{t = - \frac{3}{2} - \frac{{3\sqrt 5 }}{2}}\end{array}\)
پ
\(\begin{array}{*{20}{l}}{{n^2} - 4n = - 5}\\{{n^2} - 4n + {{\left( {\frac{{ - 4}}{2}} \right)}^2} = - 5 + {{\left( {\frac{{ - 4}}{2}} \right)}^2}}\\{{{\left( {n - 2} \right)}^2} = - 1}\\{n - 2 = \pm \sqrt { - 1} \; \otimes }\end{array}\)
ت
\(\begin{array}{*{20}{l}}{2{\mkern 1mu} {r^2} + r = 2}\\{{r^2} + \frac{1}{2}r = 1}\\{{r^2} + \frac{1}{2}r + {{\left( {\frac{1}{4}} \right)}^2} = 1 + {{\left( {\frac{1}{4}} \right)}^2}}\\{{{\left( {r + \frac{1}{4}} \right)}^2} = \frac{{17}}{{16}}}\\{r + \frac{1}{4} = \pm \frac{{\sqrt {17} }}{4}}\\{r = - \frac{1}{4} + \frac{{\sqrt {17} }}{4}}\\{r = - \frac{1}{4} - \frac{{\sqrt {17} }}{4}}\end{array}\)
گام به گام کتاب های پایه دهم
گام به گام جامع کتاب ریاضی دهم
گام به گام جامع کتاب شیمی دهم
گام به گام جامع کتاب فارسی دهم
گام به گام جامع کتاب نگارش دهم
گام به گام جامع کتاب عربی دهم
گام به گام جامع کتاب زبان انگلیسی دهم
گام به گام جامع کتاب کتاب کار انگلیسی دهم
گام به گام جامع کتاب آمادگی دفاعی دهم
گام به گام جامع کتاب دین و زندگی دهم
گام به گام جامع کتاب جغرافیای ایران دهم
گام به گام جامع کتاب آزمایشگاه علوم تجربی دهم
گام به گام جامع کتاب تفکر و سواد رسانه ای دهم
گام به گام جامع کتاب کارگاه کارآفرینی و تولید
فعالیت صفحه 74 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ فعالیت صفحه 74 درس 4
جواب فعالیت صفحه 74 درس 4 ریاضی دهم
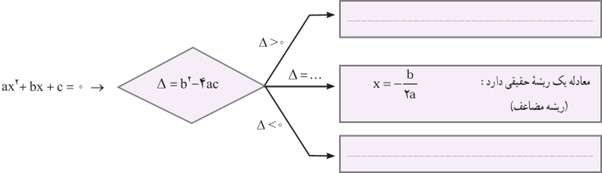
در بخش های قبل، روش هایی برای حل معادله های درجهٔ دوم فرا گرفته اید. اکنون می خواهیم یک فرمول کلی برای حل معادلهٔ درجه دوم ax2+bx+c=0 که در آن a≠0 است، پیدا کنیم.
دانش آموز: آیا با روش مربع کامل می توان هر معادلهٔ درجه دوم را حل کرد؟
معلم: بله. برای حل معادلهٔ ax2+bx+c=0 با این روش مراحل زیر را انجام می دهیم:
\(a{x^2} + bx + c = 0\)
دو طرف معادله را بر a تقسیم می کنیم \({x^2} + \frac{b}{a}x + \frac{c}{a} = 0\)
به دو طرف معادله، .... را اضافه کرده ایم \({x^2} + \frac{b}{a}x = - \frac{c}{a}\)
به دو طرف معادله، .... را اضافه کرده ایم تا سمت چپ مربع کامل شود \({x^2} + \frac{b}{a}x + .... = - \frac{c}{a} + ....\)
دو طرف را ساده کرده ایم \({(x + \frac{b}{{2a}})^2} = \frac{{{b^2} - 4ac}}{{4{a^2}}}\)
به دو طرف معادله، \( - \frac{c}{a}\) را اضافه کرده ایم \({x^2} + \frac{b}{a}x = - \frac{c}{a}\)
به دو طرف معادله، \(\frac{{{b^2}}}{{4{a^2}}}\) را اضافه کرده ایم تا سمت چپ مربع کامل شود \({x^2} + \frac{b}{a}x + \frac{{{b^2}}}{{4a}} = - \frac{c}{a} + \frac{{{b^2}}}{{4a}}\)
کاردرکلاس صفحه 75 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ کاردرکلاس صفحه 75 درس 4
جواب کاردرکلاس صفحه 75 درس 4 ریاضی دهم
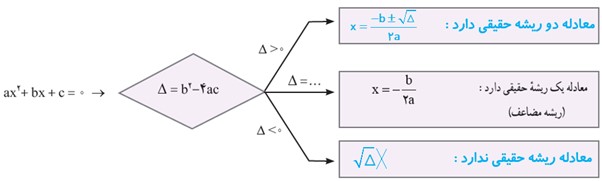
1 با توجّه به فعالیت بالا، جاهای خالی را با عبارت های مناسب پر کنید.
2 معادله های زیر را با فرمول کلی حل کنید.
الف \({x^2} - x + 1 = 0\)
ب \( - 2{x^2} + x + 3 = 0\)
پ \( - {x^2} + 4x - 4 = 0\)
الف
\(\begin{array}{*{20}{l}}\begin{array}{l}{x^2} - x + 1 = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = - \,1}\\{c = 1}\end{array}} \right.\\\\ \Rightarrow \Delta = {b^2} - 4ac = {\left( { - \,1} \right)^2} - 4\left( 1 \right)\left( 1 \right) = - 3 < 0\end{array}\end{array}\)
جواب ندارد
ب
\(\begin{array}{*{20}{l}}\begin{array}{l} - 2{x^2} + x + 3 = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - \,2}\\{b = \,1}\\{c = 3}\end{array}} \right.\\\\ \Rightarrow \Delta = {b^2} - 4ac = {\left( 1 \right)^2} - 4\left( { - 2} \right)\left( 3 \right) = 25\\\end{array}\\{x = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{ - 1 \pm 5}}{{ - 4}} \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{x_1} = \frac{3}{2}\\\end{array}\\{{x_2} = - 1}\end{array}} \right.}\end{array}\)
پ
\(\begin{array}{*{20}{l}}\begin{array}{l} - {x^2} + 4x - 4 = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 1}\\{b = \,4}\\{c = - 4}\end{array}} \right.\\\\ \Rightarrow \Delta = {b^2} - 4ac = {\left( 4 \right)^2} - 4\left( { - 1} \right)\left( { - 4} \right) = 0\\\end{array}\\{x = \frac{{ - b}}{{2a}} = \frac{{ - 4}}{{ - 2}} = 2}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
تمرین صفحه 76 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ تمرین صفحه 76 درس 4
جواب تمرین صفحه 76 درس 4 ریاضی دهم
1 معادله های زیر را به کمک تجزیه حل کنید.
1 \({x^2} - 11x = - 10\)
2 \(5{t^2} = 20\)
3 \(5{a^2} - 7a = 2a(a - 3)\)
4 \(4{k^2} - 12k + 8 = 0\)
1
\(\begin{array}{l}{x^2} - 11x = - 10\\\\ \Rightarrow {x^2} - 11\,x + 10 = 0\\\\ \Rightarrow \left( {x - 10} \right)\left( {x - 1} \right) = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x - 10 = 0 \Rightarrow x = 10\\\end{array}\\{x - 1 = 0 \Rightarrow x = 1}\end{array}} \right.\end{array}\)
2
\(\begin{array}{l}5{t^2} = 20\\\\ \Rightarrow {t^2} = 4 \Rightarrow {t^2} - 4 = 0\\\\ \Rightarrow \left( {t - 2} \right)\left( {t + 2} \right) = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}t - 2 = 0 \Rightarrow t = 2\\\end{array}\\{t + 2 = 0 \Rightarrow t = - 2}\end{array}} \right.\end{array}\)
3
\(\begin{array}{l}5{a^2} - 7a = 2a(a - 3)\\\\ \Rightarrow 5{a^2} - 7a = 2{a^2} - 6a\\\\ \Rightarrow 3{a^2} - a = 0\\\\ \Rightarrow a\left( {3a - 1} \right) = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a = 0\\\end{array}\\{3a - 1 = 0 \Rightarrow a = \frac{1}{3}}\end{array}} \right.\end{array}\)
4
\(\begin{array}{l}4{k^2} - 12k + 8 = 0\\\\ \Rightarrow {k^2} - 3k + 2 = 0\\\\ \Rightarrow \left( {k - 2} \right)\left( {k - 1} \right) = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}k - 2 = 0 \Rightarrow k = 2\\\end{array}\\{k - 1 = 0 \Rightarrow k = 1}\end{array}} \right.\end{array}\)
2 هر یک از معادله های زیر را با ریشهٔ دوم گرفتن حل کنید.
1 \({n^2} - 2 = 26\)
2 \({x^2} + 12 = 3\)
3 \({(3t - 2)^2} = 4\)
4 \(3 - 3k = 3k(2k - 1)\)
1
\(\begin{array}{l}{n^2} - 2 = 26\\\\ \Rightarrow {n^2} = 28 \Rightarrow n = \pm \sqrt {28} = \pm 2\sqrt 7 \end{array}\)
2
\(\begin{array}{l}{x^2} + 12 = 3\\\\ \Rightarrow {x^2} = - 9 \Rightarrow x = \pm \sqrt { - 9} \otimes \end{array}\)
3
\(\begin{array}{l}{(3t - 2)^2} = 4\\\\\begin{array}{*{20}{l}}\begin{array}{l} \Rightarrow 3t - 2 = \pm \sqrt 4 = \pm 2\\\\ \Rightarrow 3t = 2 \pm 2 \Rightarrow t = \frac{{2 \pm 2}}{3}\\\end{array}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}t = \frac{{2 + 2}}{3} = \frac{4}{3}\\\end{array}\\{t = \frac{{2 - 2}}{3} = 0}\end{array}} \right.}\end{array}\end{array}\)
4
\(\begin{array}{l}3 - 3k = 3k(2k - 1)\\\\\begin{array}{*{20}{l}}\begin{array}{l} \Rightarrow 3 - 3k = 6{k^2} - 3k\\\\ \Rightarrow 3 = 6{k^2}\\\\ \Rightarrow \frac{3}{6} = {k^2} = \frac{1}{2}\\\end{array}\\{ \Rightarrow k = \pm \frac{{\sqrt 2 }}{2}}\end{array}\end{array}\)
3 معادله های زیر را به روش مربع کامل حل کنید.
1 \({x^2} - 6x = 7\)
2 \({s^2} - 3x + 3 = 0\)
3 \({r^2} + 4r + 4 = 0\)
4 \(2{a^2} + 5a - 3 = 0\)
1
\(\begin{array}{*{20}{l}}\begin{array}{l}{x^2} - 6x = 7\\\\ \Rightarrow {x^2} - 6x + {\left( {\frac{{ - 6}}{2}} \right)^2} = 7 + {\left( {\frac{{ - 6}}{2}} \right)^2}\\\\ \Rightarrow {\left( {x - 3} \right)^2} = 7 + 9 = 16\\\end{array}\\\begin{array}{l} \Rightarrow x - 3 = \pm 4\\\\ \Rightarrow x = 3 \pm 4 \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x = 7\\\end{array}\\{x = - 1}\end{array}} \right.\end{array}\end{array}\)
2
\(\begin{array}{*{20}{l}}\begin{array}{l}{s^2} - 3x + 3 = 0\\\\ \Rightarrow {s^2} - 3s = - 3\\\\ \Rightarrow {s^2} - 3s + {\left( {\frac{{ - 3}}{2}} \right)^2} = - 3 + {\left( {\frac{{ - 3}}{2}} \right)^2} = - 0/75\\\end{array}\\\begin{array}{l} \Rightarrow {\left( {s - 2/25} \right)^2} = - 0/75\\\\ \Rightarrow s - 2/25 = \pm \sqrt { - 0/75} \otimes \end{array}\end{array}\)
3
\(\begin{array}{l}{r^2} + 4r + 4 = 0\\\\ \Rightarrow {\left( {r + 2} \right)^2} = 0 \Rightarrow r + 2 = 0 \Rightarrow r = - 2\end{array}\)
4
\(\begin{array}{*{20}{l}}\begin{array}{l}2{a^2} + 5a - 3 = 0\\\\ \Rightarrow 2{a^2} + 5a = 3\\\\ \Rightarrow {a^2} + \frac{5}{2}a = \frac{3}{2}\\\\ \Rightarrow {a^2} + \frac{5}{2}a + {\left( {\frac{5}{4}} \right)^2} = \frac{3}{2} + {\left( {\frac{5}{4}} \right)^2}\end{array}\\\begin{array}{l}\\ \Rightarrow {\left( {a + \frac{5}{4}} \right)^2} = \frac{{49}}{{16}}\\\\ \Rightarrow a + \frac{5}{4} = \pm \frac{7}{4}\\\\ \Rightarrow a = - \frac{5}{4} \pm \frac{7}{4}\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a = - 3\\\end{array}\\{a = \frac{1}{2}}\end{array}} \right.\end{array}\end{array}\)
4 هر یک از معادله های زیر را با روش فرمول کلی حل کنید.
1 \(4{x^2} - 13x + 3 = 0\)
2 \(r - {r^2} = 3\)
3 \({a^2} + 2\sqrt 3 a = 9\)
4 \(\frac{{{t^2}}}{3} - \frac{t}{2} - \frac{3}{2} = 0\)
1
\(\begin{array}{*{20}{l}}\begin{array}{l}4{x^2} - 13x + 3 = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 4}\\{b = - 13}\\{c = 3}\end{array}} \right.\\\\ \Rightarrow \Delta = {b^2} - 4ac = {\left( { - 13} \right)^2} - 4\left( 4 \right)\left( 3 \right) = 121\\\end{array}\\\begin{array}{l} \Rightarrow x = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{13 \pm 11}}{{12}}\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{x_1} = \frac{{13 + 11}}{8} = 3\\\end{array}\\{{x_2} = \frac{{13 - 11}}{8} = \frac{1}{4}}\end{array}} \right.\end{array}\end{array}\)
2
\(\begin{array}{*{20}{l}}\begin{array}{l}r - {r^2} = 3\\\\ \Rightarrow - {r^2} + r - 3 = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 1}\\{b = 1}\\{c = - 3}\end{array}} \right.\\\\ \Rightarrow \Delta = {b^2} - 4ac = {\left( 1 \right)^2} - 4\left( { - 1} \right)\left( { - 3} \right) = 1 - 12\\\end{array}\\{ \Rightarrow \Delta = - 11 < 0}\end{array}\)
جواب ندارد
3
\(\begin{array}{l}{a^2} + 2\sqrt 3 a = 9\\\\\begin{array}{*{20}{l}}\begin{array}{l} \Rightarrow {a^2} + 2\sqrt 3 a - 9 = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 2\sqrt 3 }\\{c = - 9}\end{array}} \right.\\\end{array}\\\begin{array}{l} \Rightarrow \Delta = {b^2} - 4ac = {\left( {2\sqrt 3 } \right)^2} - 4\left( 1 \right)\left( { - 9} \right)\\\end{array}\\\begin{array}{l} \Rightarrow \Delta = 48\\\\ \Rightarrow x = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{ - 2\sqrt 3 \pm 4\sqrt 3 }}{2} = - \sqrt 3 \pm 2\sqrt 3 \\\end{array}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{x_1} = - \,3\sqrt 3 \\\end{array}\\{{x_2} = \sqrt 3 }\end{array}} \right.}\end{array}\end{array}\)
4
\(\begin{array}{*{20}{l}}\begin{array}{l}\frac{{{t^2}}}{3} - \frac{t}{2} - \frac{3}{2} = 0\\\\\mathop \Rightarrow \limits^{ \times 6} \,2{t^2} - 3t - 4 = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = - 3}\\{c = - 4}\end{array}} \right.\\\\ \Rightarrow \Delta = {b^2} - 4ac = {\left( { - 3} \right)^2} - 4\left( 2 \right)\left( { - 4} \right) = 41\\\end{array}\\\begin{array}{l} \Rightarrow x = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{3 \pm \sqrt {41} }}{4}\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{x_1} = \frac{{3 + \sqrt {41} }}{4}\\\end{array}\\{{x_2} = \frac{{3 - \sqrt {41} }}{4}}\end{array}} \right.\end{array}\end{array}\)
5 هر یک از معادله های زیر را به روش دلخواه حل کنید.
1 \(2{x^2} = 250\)
2 \(9 - 6z + {z^2} = 0\)
3 \(4{a^2} + 3a = 1\)
4 \({b^2} + \sqrt 2 b - 4 = 0\)
1
با روش ریشه گیری:
\({x^2} = 125 \Rightarrow x = \pm 5\sqrt 5 \)
2
با روش مربع کامل:
\({\left( {z - 3} \right)^2} = 0 \Rightarrow z - 3 = 0 \Rightarrow z = 3\)
3
با روش فرمول کلی:
\(\begin{array}{*{20}{l}}\begin{array}{l}4{a^2} + 3a - 1 = 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{A = 4}\\{B = 3}\\{C = - 1}\end{array}} \right.\\\\ \Rightarrow \Delta = {B^2} - 4AC = {\left( 3 \right)^2} - 4\left( 4 \right)\left( { - 1} \right) = 25\\\end{array}\\\begin{array}{l} \Rightarrow a = \frac{{ - B \pm \sqrt \Delta }}{{2A}} = \frac{{ - 3 \pm \sqrt {25} }}{8}\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{a_1} = \frac{{ - 3 + 5}}{8} = \frac{1}{4}\\\end{array}\\{{a_2} = \frac{{ - 3 - 5}}{8} = - 1}\end{array}} \right.\end{array}\end{array}\)
4
با روش فرمول کلی:
\(\begin{array}{*{20}{l}}\begin{array}{l} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{A = 1}\\{B = \sqrt 2 }\\{C = - 4}\end{array}} \right.\\\\ \Rightarrow \Delta = {B^2} - 4AC = {\left( {\sqrt 2 } \right)^2} - 4\left( 1 \right)\left( { - 4} \right) = 18\\\end{array}\\\begin{array}{l} \Rightarrow b = \frac{{ - B \pm \sqrt \Delta }}{{2A}} = \frac{{ - \sqrt 2 \pm 3\sqrt 2 }}{2}\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{b_1} = \frac{{ - \sqrt 2 + 3\sqrt 2 }}{2} = \sqrt 2 \\\end{array}\\{{b_2} = \frac{{ - \sqrt 2 - 3\sqrt 2 }}{2} = - 2\sqrt 2 }\end{array}} \right.\end{array}\end{array}\)
6 مجموع مربعات دو عدد فرد متوالی 290 است. این دو عدد را پیدا کنید.
فرض کنیم که n یک عدد فرد باشد؛ بنابراین 2n+ یک عدد فرد است. در نتیجه داریم :
\(\begin{array}{*{20}{l}}\begin{array}{l}{n^2} + {\left( {n + 2} \right)^2} = 290\\\\ \Rightarrow {n^2} + {n^2} + 4n + 4 = 2{n^2} + 4n + 4 = 290\\\end{array}\\\begin{array}{l} \Rightarrow {n^2} + 2n + 2 = 145\\\\ \Rightarrow {n^2} + 2n = 143\\\\ \Rightarrow {n^2} + 2n + {\left( {\frac{2}{2}} \right)^2} = 143 + {\left( {\frac{2}{2}} \right)^2}\\\end{array}\\\begin{array}{l} \Rightarrow {\left( {n + 1} \right)^2} = 144\\\\ \Rightarrow n + 1 = \pm 12\\\\ \Rightarrow n = - 1 \pm 12\\\end{array}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}n = - 1 + 12 \Rightarrow n = 11 \Rightarrow \begin{array}{*{20}{c}}{}&{}\end{array}11\,,\,13\\\end{array}\\{n = - 1 - 12 \Rightarrow n = - 13 \Rightarrow \begin{array}{*{20}{c}}{}&{}\end{array} - 13\,,\, - 11}\end{array}} \right.}\end{array}\)
7 طول یک مستطیل 3 سانتی متر بیشتر از 4 برابر عرض آن است. اگر مساحت این مستطیل 45 سانتی متر مربع باشد، ابعاد این مستطیل را مشخص کنید.
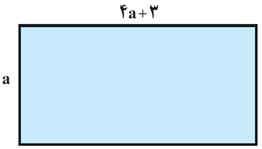
\(\begin{array}{*{20}{l}}\begin{array}{l}a\,,\,4a + 3\\\\ \Rightarrow a\left( {4a + 3} \right) = 45\\\\ \Rightarrow 4{a^2} + 3a - 45 = 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{A = 4}\\{B = 3}\\{C = - 45}\end{array}} \right.\\\end{array}\\\begin{array}{l} \Rightarrow \Delta = {B^2} - 4AC = {\left( 3 \right)^2} - 4\left( 4 \right)\left( { - 45} \right) = 729\\\end{array}\\\begin{array}{l} \Rightarrow a = \frac{{ - B \pm \sqrt \Delta }}{{2A}} = \frac{{ - 3 \pm \sqrt {729} }}{8} = \frac{{ - 3 \pm 27}}{8}\\\end{array}\\\begin{array}{l} \Rightarrow {a_1} = \frac{{ - 3 - 27}}{8} = - \frac{{15}}{4}\, \otimes \\\end{array}\\{ \Rightarrow {a_2} = \frac{{ - 3 + 27}}{8} = 3}\\\begin{array}{l}\\ \Rightarrow a = 3\end{array}\end{array}\)
بنابراین:
عرض = 3 و طول = 15
8 اختلاف سنی دو برادر با یکدیگر 4 سال است. اگر چهار سال دیگر حاصل ضرب سن آنها 60 شود، سن هر کدام چقدر است؟
\(\begin{array}{*{20}{l}}\begin{array}{l}n\;\;{\mkern 1mu} {\kern 1pt} ,\;\;{\mkern 1mu} {\kern 1pt} n + 4\,\,\,\\\\ \Rightarrow \left( {n + 4} \right)\left( {n + 4 + 4} \right) = 60\\\\ \Rightarrow \left( {n + 4} \right)\left( {n + 8} \right) = 60\\\end{array}\\\begin{array}{l} \Rightarrow {n^2} + 12n + 32 = 60\\\\ \Rightarrow {n^2} + 12n = 28\\\\ \Rightarrow {n^2} + 12n + {\left( {\frac{{12}}{2}} \right)^2} = 28 + {\left( {\frac{{12}}{2}} \right)^2}\\\end{array}\\\begin{array}{l} \Rightarrow {\left( {n + 6} \right)^2} = 64 \Rightarrow n + 6 = \pm \sqrt {64} \\\\ \Rightarrow n = - 6 \pm 8\\\end{array}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{n = 2}\\{n = - 14 \otimes }\end{array}} \right.\,\,\,\, \Rightarrow n = 2}\end{array}\)
2 سال و 6 سال سن دارند.
9 یک عکس به اندازهٔ 10 در 15 سانتی متر درون یک قاب با مساحت 300 سانتی متر مربع، قرار دارد. اگر فاصلهٔ همهٔ لبه های عکس تا قاب برابر باشد، ابعاد این قاب عکس را پیدا کنید.
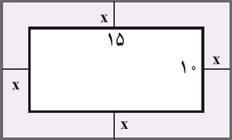
\(\begin{array}{*{20}{l}}\begin{array}{l}\left( {10 + 2x} \right)\left( {15 + 2x} \right) = 300\\\\ \Rightarrow 4{x^2} + 50x + 150 = 300\\\\ \Rightarrow 4{x^2} + 50x - 150 = 0\\\end{array}\\\begin{array}{l} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 4}\\{b = 50}\\{c = - 150}\end{array}} \right.\\\\ \Rightarrow \Delta = {b^2} - 4ac = {\left( {50} \right)^2} - 4\left( 4 \right)\left( { - 150} \right) = 4900\\\end{array}\\\begin{array}{l} \Rightarrow x = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{ - 50 \pm \sqrt {4900} }}{8} = \frac{{ - 50 \pm 70}}{8}\\\end{array}\\\begin{array}{l}{x_1} = \frac{{ - 50 - 70}}{8} = - 15\\\end{array}\\{{x_2} = \frac{{ - 50 + 70}}{8} = 2/5 \Rightarrow x = 2/5}\end{array}\)
بنابراین:
عرض = 15 و طول = 20
10- در یک تیمگان (لیگ) والیبال، 45 بازی انجام شده است. اگر هر تیم با دیگر تیم های تیمگان، تنها یک بازی انجام داده باشد، تعداد تیم های این تیمگان را به دست آورید. اگر تعداد بازی های تیمگان N و تعداد تیم ها n باشد، الگویی برای تعداد بازی ها به دست آورید.

اگر تعداد تیم ها را n و هر تیم 1-n بازی دارد. پس با توجه به اینکه بین هر دو تیم تنها یک بازی صورت می گیرد و اصطلاحاً رفت و برگشتی نیست. در نتیجه کل بازی ها برابر \(\frac{{n\left( {n - 1} \right)}}{2}\) است. بنابراین:
: الگو برای تعداد بازی ها \(\frac{{n\left( {n - 1} \right)}}{2}\)
\(\begin{array}{*{20}{l}}\begin{array}{l}\frac{{n\left( {n - 1} \right)}}{2} = 45 \Rightarrow n\left( {n - 1} \right) = 90\\\\ \Rightarrow {n^2} - n - 90 = 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = - 1}\\{c = - 90}\end{array}} \right.\\\end{array}\\\begin{array}{l} \Rightarrow \Delta = {b^2} - 4ac = {\left( { - 1} \right)^2} - 4\left( 1 \right)\left( { - 90} \right) = 361\\\end{array}\\\begin{array}{l}n = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{1 \pm 19}}{2} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{n_1} = \frac{{1 - 19}}{2} = - 9 \otimes }\\{{n_2} = \frac{{1 + 19}}{2} = 10}\end{array}} \right.\,\,\,\,\\\\ \Rightarrow n = 10\;\;\;\;N = n - 1\end{array}\end{array}\)
10 تیم
11 فشار خون نرمال 1 یک شخص مذکر، که بر حسب میلی متر جیوه (mmHg) اندازه گیری می شود، با رابطهٔ\(P = 0/006{s^2} - 0/02s + 120\) محاسبه می شود که در آن، P فشار خون نرمال یک فرد با سن s است. سن شخصی را پیدا کنید که فشار خون آن 125 میلی متر جیوه باشد. (از ماشین حساب استفاده کنید.)

\(\begin{array}{*{20}{l}}\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}P = 0/006{s^2} - 0/02s + 120\\\end{array}\\{{P_1} = 125}\end{array}} \right.\\\\ \Rightarrow 125 = 0/006{s^2} - 0/02s + 120\\\\ \Rightarrow 0/006{s^2} - 0/02s - 5 = 0\\\end{array}\\\begin{array}{l} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 0/006}\\{b = - 0/02}\\{c = - 5}\end{array}} \right.\\\\ \Rightarrow \Delta = {b^2} - 4ac = {\left( { - 0/02} \right)^2} - 4\left( {0/006} \right)\left( { - 5} \right) = 0/1204\\\end{array}\\\begin{array}{l} \Rightarrow s = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{0/02 \pm \sqrt {0/1204} }}{{0/012}}\\\\ \Rightarrow s = \frac{{0/02 + \sqrt {0/1204} }}{{0/012}} \simeq 31\end{array}\end{array}\)
31 سال
گام به گام کتاب های پایه دهم
گام به گام جامع کتاب ریاضی دهم
گام به گام جامع کتاب شیمی دهم
گام به گام جامع کتاب فارسی دهم
گام به گام جامع کتاب نگارش دهم
گام به گام جامع کتاب عربی دهم
گام به گام جامع کتاب زبان انگلیسی دهم
گام به گام جامع کتاب کتاب کار انگلیسی دهم
گام به گام جامع کتاب آمادگی دفاعی دهم
گام به گام جامع کتاب دین و زندگی دهم
گام به گام جامع کتاب جغرافیای ایران دهم
گام به گام جامع کتاب آزمایشگاه علوم تجربی دهم
گام به گام جامع کتاب تفکر و سواد رسانه ای دهم
گام به گام جامع کتاب کارگاه کارآفرینی و تولید
فعالیت صفحه 78 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ فعالیت صفحه 78 درس 4
جواب فعالیت صفحه 78 درس 4 ریاضی دهم
معادلۀ y=x2-4 را درنظر بگیرید.
الف در جدول زیر، چند نقطه که در این معادله صدق می کنند، آمده است. این جدول را کامل کنید.

نقاط به دست آمده در جدول بالا را در یک دستگاه مختصات مشخص کرده و آنها را به یکدیگر وصل می کنیم (شکل های روبه رو).
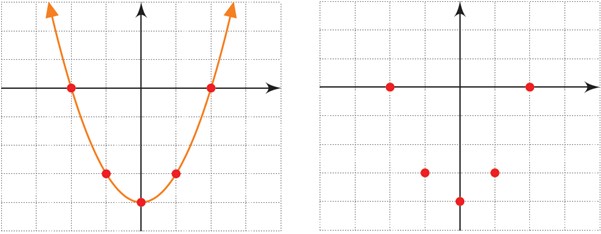
ب پایین ترین نقطهٔ این نمودار چه نقطه ای است؟ آیا می توانید محور تقارن این نمودار را مشخص کنید؟
پ برای رسم این نمودار، از چند نقطه استفاده کرده ایم؟ آیا با نقاط کمتری نیز می توانیم این نمودار را رسم کنیم؟
ت محل برخورد منحنی رسم شده با محور xها در چه نقاطی است؟
الف
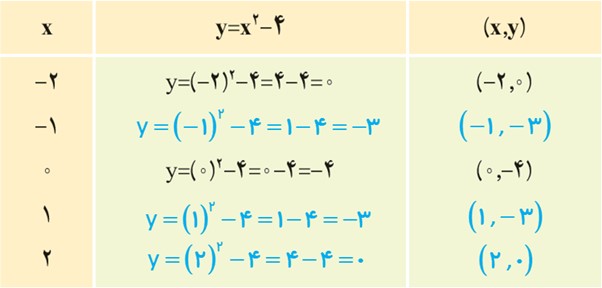
ب
نقطه (0, -4) پایین ترین نقطه این نمودار است؛ محور y ، محور تقارن این شکل است.
پ
با 5 نقطه ؛ بله ، با سه نقطه نیز می توان این شکل را رسم کرد.
ت
این منحنی محور x را در نقاط (-2, 0) و (2, 0) قطع می کند.
فعالیت صفحه 79 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ فعالیت صفحه 79 درس 4
جواب فعالیت صفحه 79 درس 4 ریاضی دهم
معادلهٔ یک سهمی به صورت \(y = {x^2} - 4x + 5\) است.
الف سمت راست این معادله را به شکل مربع کامل بنویسید.
\(y = {x^2} - 4x + 5\;\; \Rightarrow \;\;y = {\left( {x - 2} \right)^2} + ....\)
ب ریشهٔ عبارت داخل پرانتز را به دست آورید و آن را در ردیف وسط جدول زیر قرار دهید. جاهای خالی را با عبارت های مناسب پر کنید.
\(x - 2 = 0\; \Rightarrow \;...........\)
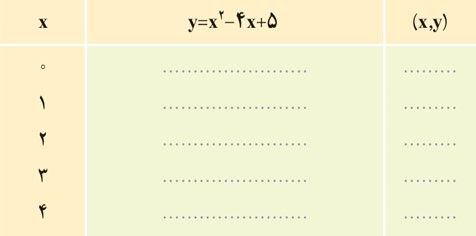
پ پنج نقطهٔ حاصل شده در جدول بالا را به یکدیگر وصل کنید تا این سهمی رسم شود.
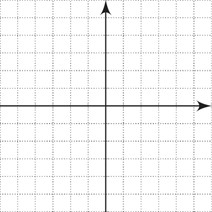
ت آیا می توانید پایین ترین نقطهٔ این سهمی را از معادلهٔ آن به شکل \(y = {\left( {x - 2} \right)^2} + 1\) به دست آورید.
الف
\(y = {x^2} - 4x + 5\;\; \Rightarrow \;\;y = {\left( {x - 2} \right)^2} + 1\)
ب
\(x - 2 = 0\; \Rightarrow \;x = 2\)
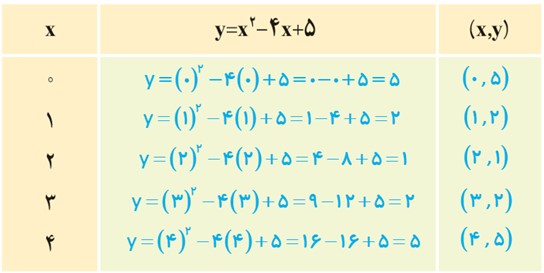
پ
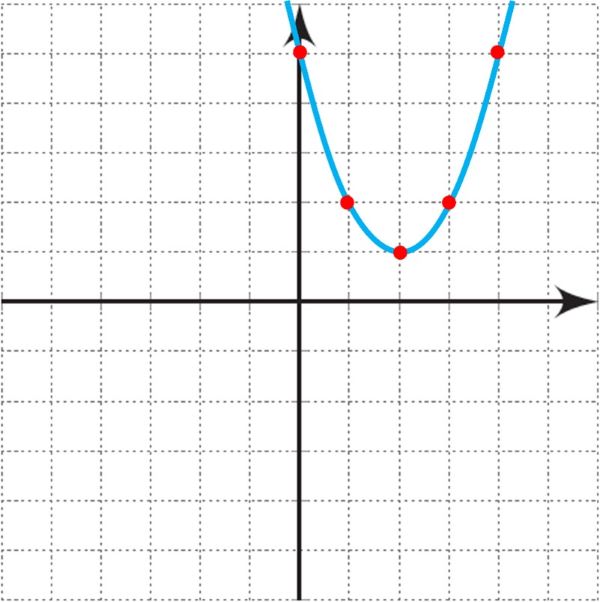
ت
طول این نقطه برابر با ریشه داخل پرانتز است و عرض آن از جایگذاری ریشه در تابع منحنی بدست می آید:
\(\begin{array}{*{20}{l}}{y = {{\left( {x - 2} \right)}^2} + 1 \Rightarrow x - 2 = 0 \Rightarrow {x_0} = 2 \Rightarrow {y_0} = {{\left( {2 - 2} \right)}^2} + 1 = 1}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = 2}\\{{y_0} = 1}\end{array}} \right. \Rightarrow \left( {2\,,\,1} \right)}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
کاردرکلاس صفحه 80 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ کاردرکلاس صفحه 80 درس 4
جواب کاردرکلاس صفحه 80 درس 4 ریاضی دهم
1 در هر یک از سهمی های زیر، رأس را مشخص و سپس آن را رسم کنید.
الف \(y = {\left( {x + 1} \right)^2} - 2\)
ب \(y = - 2{x^2} + 1\)
الف
\(\begin{array}{*{20}{l}}\begin{array}{l}y = {\left( {x + 1} \right)^2} - 2 \Rightarrow x + 1 = 0 \Rightarrow {x_0} = - 1\\\\ \Rightarrow {y_0} = {\left( { - 1 + 1} \right)^2} - 2 = - 2\end{array}\\\begin{array}{l}\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = - 1}\\{{y_0} = - 2}\end{array}} \right. \Rightarrow \left( { - 1\,,\, - 2} \right)\end{array}\end{array}\)
نقطه رأس: (-1, -2)
\(\begin{array}{*{20}{l}}{{x_1} = - 2 \Rightarrow {y_1} = {{\left( { - 2 + 1} \right)}^2} - 2 = - 1}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = - 2}\\{{y_1} = - 1}\end{array}} \right. \Rightarrow \left( { - 2\,,\, - 1} \right)}\\{{x_2} = 0 \Rightarrow {y_2} = {{\left( {0 + 1} \right)}^2} - 2 = - 1}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_2} = 0}\\{{y_2} = - 1}\end{array}} \right. \Rightarrow \left( {0\,,\, - 1} \right)}\end{array}\)
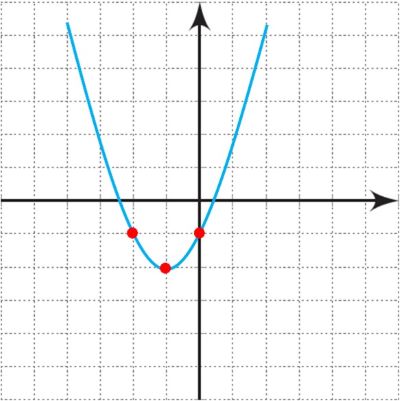
ب
\(\begin{array}{*{20}{l}}{y = - 2{x^2} + 1 \Rightarrow {x_0} = 0 \Rightarrow {y_0} = - 2{{\left( 0 \right)}^2} + 1 = 1}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = 0}\\{{y_0} = 1}\end{array}} \right. \Rightarrow \left( {0\,,\,1} \right)}\end{array}\)
نقطه رأس: (0, 1)
\(\begin{array}{*{20}{l}}{{x_1} = - 1 \Rightarrow {y_1} = - 2{{\left( { - 1} \right)}^2} + 1 = - 1}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = - 1}\\{{y_1} = - 1}\end{array}} \right. \Rightarrow \left( { - 1\,,\, - 1} \right)}\\{{x_2} = 1 \Rightarrow {y_2} = - 2{{\left( 1 \right)}^2} + 1 = - 1}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_2} = 1}\\{{y_2} = - 1}\end{array}} \right. \Rightarrow \left( {1\,,\, - 1} \right)}\end{array}\)

گام به گام کتاب های پایه دهم
گام به گام جامع کتاب ریاضی دهم
گام به گام جامع کتاب شیمی دهم
گام به گام جامع کتاب فارسی دهم
گام به گام جامع کتاب نگارش دهم
گام به گام جامع کتاب عربی دهم
گام به گام جامع کتاب زبان انگلیسی دهم
گام به گام جامع کتاب کتاب کار انگلیسی دهم
گام به گام جامع کتاب آمادگی دفاعی دهم
گام به گام جامع کتاب دین و زندگی دهم
گام به گام جامع کتاب جغرافیای ایران دهم
گام به گام جامع کتاب آزمایشگاه علوم تجربی دهم
گام به گام جامع کتاب تفکر و سواد رسانه ای دهم
گام به گام جامع کتاب کارگاه کارآفرینی و تولید
فعالیت صفحه 80 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ فعالیت صفحه 80 درس 4
جواب فعالیت صفحه 80 درس 4 ریاضی دهم
معادلهٔ سهمی به صورت \(y = a{x^2} + bx + c\) را در نظر بگیرید.
الف سمت راست این معادله را به شکل مربع کامل بنویسید و نشان دهید:
\(y = a{\left( {x + \frac{b}{{2a}}} \right)^2} + \frac{{4ac - {b^2}}}{{4a}}\)
ب با استفاده از قسمت قبل، نشان دهید که رأس این سهمی، نقطهٔ \(\left( { - \frac{b}{{2a}}\;,\;\frac{{4ac - {b^2}}}{{4a}}} \right)\) و خط تقارن آن نیز \(x = - \frac{b}{{2a}}\) است.
الف
\(\begin{array}{*{20}{l}}\begin{array}{l}y = a{x^2} + bx + c\\\\ \Rightarrow y = a\left( {{x^2} + \frac{b}{a}x} \right) + c\\\\ \Rightarrow y = a\left( {{x^2} + \frac{b}{a}x + {{\left( {\frac{b}{{2a}}} \right)}^2} - {{\left( {\frac{b}{{2a}}} \right)}^2}} \right) + c\end{array}\\\begin{array}{l}\\ \Rightarrow y = y = a\left( {{x^2} + \frac{b}{a}x + \frac{{{b^2}}}{{4{a^2}}}} \right) + c - \frac{{{b^2}}}{{4a}}\\\\ \Rightarrow y = a{\left( {x + \frac{b}{{2a}}} \right)^2} + \frac{{4ac - {b^2}}}{{4a}}\end{array}\end{array}\)
ب
\(\begin{array}{*{20}{l}}\begin{array}{l}x + \frac{b}{{2a}} = 0\\\\ \Rightarrow {x_0} = - \frac{b}{{2a}}\\\\ \Rightarrow {y_0} = a{\left( { - \frac{b}{{2a}} + \frac{b}{{2a}}} \right)^2} + \frac{{4ac - {b^2}}}{{4a}} = \frac{{4ac - {b^2}}}{{4a}}\\\end{array}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{x_0} = - \frac{b}{{2a}}\\\end{array}\\{{y_0} = \frac{{4ac - {b^2}}}{{4a}}}\end{array}} \right.}\end{array}\)
فعالیت صفحه 81 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ فعالیت صفحه 81 درس 4
جواب فعالیت صفحه 81 درس 4 ریاضی دهم
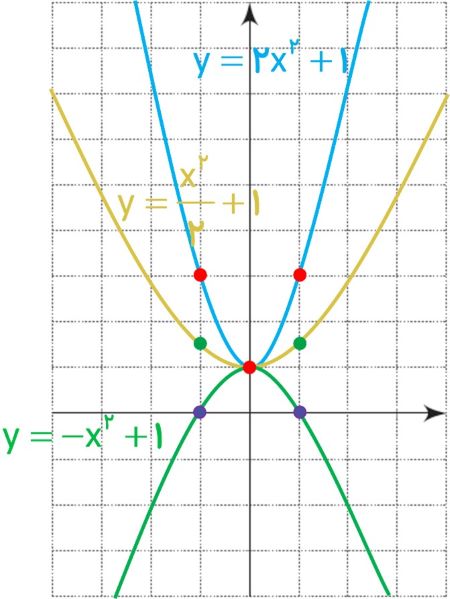
معادلهٔ دو سهمی به صورت \(y = \frac{{{x^2}}}{2} + 1\) و \(y = 2{x^2} + 1\) است.
الف مختصات رأس و دو نقطه دیگر از این دو سهمی را در جدول زیر مشخص کنید و سپس نمودار هر دو سهمی را در شکل مقابل رسم کنید و نشان دهید که مختصات رأس هر دو سهمی نقطۀ A(0,1) است.
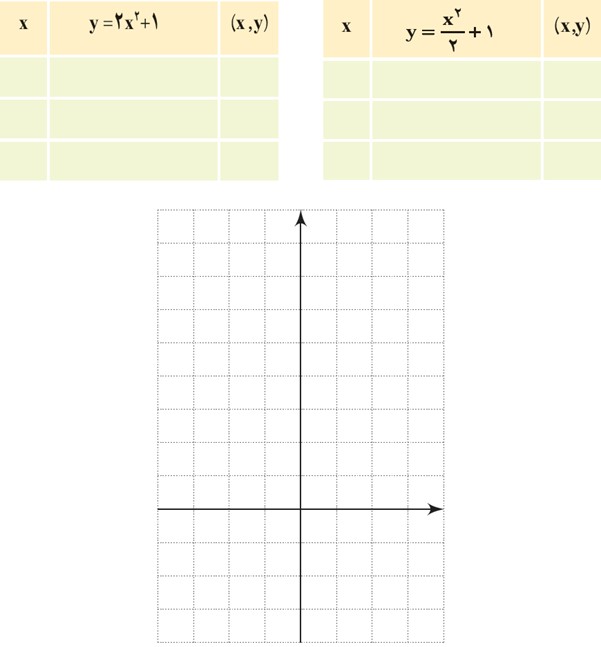
ب معادلهٔ سهمی دیگری را که نقطهٔ A رأس آن است، بنویسید و آن را در دستگاه بالا رسم کنید.
الف

ب
\(\begin{array}{*{20}{l}}{y = - {x^2} + 1}\\{ \Rightarrow {x_0} = 0 \Rightarrow {y_0} = - {{\left( 0 \right)}^2} + 1 = 0 + 1 = 1}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = 0}\\{{y_0} = 1}\end{array}} \right.}\\{ \Rightarrow {x_1} = - 1 \Rightarrow {y_1} = - {{\left( { - 1} \right)}^2} + 1 = - 1 + 1 = 0}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = - 1}\\{{y_1} = 0}\end{array}} \right.}\\{ \Rightarrow {x_2} = 1 \Rightarrow {y_2} = - {{\left( 1 \right)}^2} + 1 = - 1 + 1 = 0}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_2} = - 1}\\{{y_2} = 0}\end{array}} \right.}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
تمرین صفحه 81 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ تمرین صفحه 81 درس 4
جواب تمرین صفحه 81 درس 4 ریاضی دهم
1 نمودار هر یک از سهمی های زیر را رسم کنید.
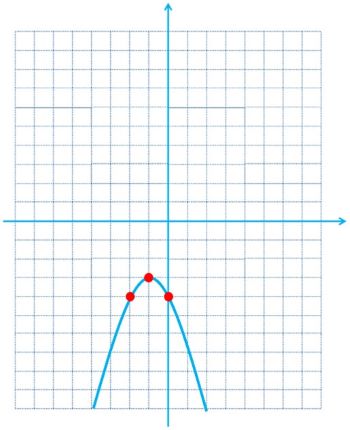
الف \(y = - {\left( {x + 1} \right)^2} - 3\)
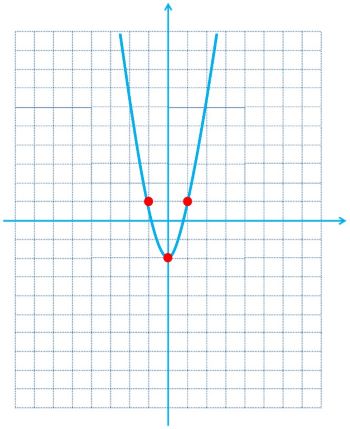
ب \(y = 3{x^2} - 2\)
پ \(y = x - {x^2}\)
ت \(y = \frac{{{x^2}}}{2} + x - 4\)
الف
\(\begin{array}{*{20}{l}}{y = - {{\left( {x + 1} \right)}^2} - 3}\\{x + 1 = 0 \Rightarrow {x_0} = - 1 \Rightarrow {y_0} = - {{\left( { - 1 + 1} \right)}^2} - 3 = 0 - 3 = - 3}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = - 1}\\{{y_0} = - 3}\end{array}} \right.}\\{ \Rightarrow {x_1} = - 2 \Rightarrow {y_1} = - {{\left( { - 2 + 1} \right)}^2} - 3 = - 1 - 3 = - 4}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = - 2}\\{{y_1} = - 4}\end{array}} \right.}\\{ \Rightarrow {x_2} = 0 \Rightarrow {y_2} = - {{\left( {0 + 1} \right)}^2} - 3 = - 1 - 3 = - 4}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_2} = 0}\\{{y_2} = - 4}\end{array}} \right.}\end{array}\)
ب
\(\begin{array}{*{20}{l}}{y = 3{x^2} - 2}\\{{x_0} = 0 \Rightarrow {y_0} = 3{{\left( 0 \right)}^2} - 2 = 0 - 2 = - 2}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = 0}\\{{y_0} = - 2}\end{array}} \right.}\\{{x_1} = - 1 \Rightarrow {y_1} = 3{{\left( { - 1} \right)}^2} - 2 = 3 - 2 = 1}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = - 1}\\{{y_1} = 1}\end{array}} \right.}\\{{x_2} = 1 \Rightarrow {y_2} = 3{{\left( 1 \right)}^2} - 2 = 3 - 2 = 1}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_2} = 1}\\{{y_2} = 1}\end{array}} \right.}\end{array}\)
پ
\(\begin{array}{*{20}{l}}{y = x - {x^2} = - {{\left( {x - \frac{1}{2}} \right)}^2} + \frac{1}{4}}\\{x - \frac{1}{2} = 0 \Rightarrow {x_0} = \frac{1}{2} \Rightarrow {y_0} = - {{\left( {\frac{1}{2} - \frac{1}{2}} \right)}^2} + \frac{1}{4} = 0 + \frac{1}{4} = \frac{1}{4}}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = \frac{1}{2}}\\{{y_0} = \frac{1}{4}}\end{array}} \right.}\\{{x_1} = - \frac{1}{2} \Rightarrow {y_1} = - {{\left( { - \frac{1}{2} - \frac{1}{2}} \right)}^2} + \frac{1}{4} = - 1 + \frac{1}{4} = - \frac{3}{4}}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = - \frac{1}{2}}\\{{y_1} = - \frac{3}{4}}\end{array}} \right.}\\{{x_2} = \frac{3}{2} \Rightarrow {y_2} = - {{\left( {\frac{3}{2} - \frac{1}{2}} \right)}^2} + \frac{1}{4} = - 1 + \frac{1}{4} = - \frac{3}{4}}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_2} = \frac{3}{2}}\\{{y_2} = - \frac{3}{4}}\end{array}} \right.}\end{array}\)
ت
\(\begin{array}{*{20}{l}}{y = \frac{{{x^2}}}{2} + x - 4 = \frac{1}{2}{{\left( {x + 1} \right)}^2} - \frac{9}{2}}\\{x + 1 = 0 \Rightarrow {x_0} = - 1 \Rightarrow {y_0} = \frac{1}{2}{{\left( { - 1 + 1} \right)}^2} - \frac{9}{2} = 0 - \frac{9}{2} = - \frac{9}{2}}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = - 1}\\{{y_0} = - \frac{9}{2}}\end{array}} \right.}\\{{x_1} = - 2 \Rightarrow {y_1} = \frac{1}{2}{{\left( { - 2 + 1} \right)}^2} - \frac{9}{2} = \frac{1}{2} - \frac{9}{2} = - 4}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = - 2}\\{{y_1} = - 4}\end{array}} \right.}\\{{x_2} = 0 \Rightarrow {y_2} = \frac{1}{2}{{\left( {0 + 1} \right)}^2} - \frac{9}{2} = \frac{1}{2} - \frac{9}{2} = - 4}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_2} = 0}\\{{y_2} = - 4}\end{array}} \right.}\end{array}\)
2 اگر (-2,5) و (0,5) دو نقطه از یک سهمی باشند، خط تقارن این سهمی را به دست آورید.
با توجه به اینکه عرض نقاط یکسان است، این دو نقطه نسبت به محور تقارن قرینه یکدیگرند؛ به عبارت دیگر محور تقارن از وسط طول های این دو نقطه می گذرد ؛ یعنی:
\({x_0} = \frac{{0 + ( - 2)}}{2} = - 1\)
در نتیجه خط 1-=x محور تقارن سهمی می باشد.
3 نمودار سهمی \(y = a{x^2} + bx + c\) ، محور yها را در نقطه ای به عرض 2 و محور xها را در نقاط به طول 1- و 2 قطع کرده است. معادلهٔ این سهمی را بنویسید و آن را رسم کنید.
\(\begin{array}{l}\begin{array}{*{20}{l}}\begin{array}{l}\left( {0{\kern 1pt} ,{\kern 1pt} 2} \right) \Rightarrow 2 = a{\left( 0 \right)^2} + b\left( 0 \right) + c \Rightarrow c = 2\\\end{array}\\\begin{array}{l}\left( { - 1{\kern 1pt} ,{\kern 1pt} 0} \right) \Rightarrow 0 = a{\left( { - 1} \right)^2} + b\left( { - 1} \right) + 2 \Rightarrow a - b = - 2\\\end{array}\\\begin{array}{l}\left( {2{\kern 1pt} ,{\kern 1pt} 0} \right) \Rightarrow 0 = a{\left( 2 \right)^2} + b\left( 2 \right) + 2 \Rightarrow 4a + 2b = - 2\\\end{array}\\{\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a - b = - 2\\\end{array}\\{4a + 2b = - 2}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a = - 1\\\end{array}\\{b = - 1}\end{array}} \right. \Rightarrow y = - {x^2} + x + 2}\end{array}\\\\\begin{array}{*{20}{l}}{y = - {x^2} + x + 2 = - {{\left( {x - \frac{1}{2}} \right)}^2} + \frac{9}{4}}\\\begin{array}{l}\\x - \frac{1}{2} = 0 \Rightarrow {x_0} = \frac{1}{2} \Rightarrow {y_0} = - {\left( {\frac{1}{2} - \frac{1}{2}} \right)^2} + \frac{9}{4} = \frac{9}{4}\end{array}\\\begin{array}{l}\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = \frac{1}{2}}\\{{y_0} = \frac{9}{4}}\end{array}} \right.\;\;{\mkern 1mu} {\kern 1pt} ,\;\;{\mkern 1mu} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}}{{x_1} = - 1}\\{{y_1} = 0}\end{array}} \right.\;\;{\mkern 1mu} {\kern 1pt} ,\;\;{\mkern 1mu} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}}{{x_2} = 2}\\{{y_2} = 0}\end{array}} \right.\end{array}\end{array}\end{array}\)
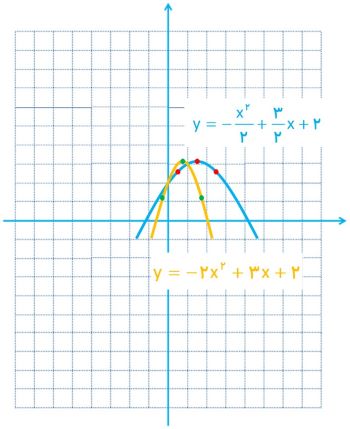
4 دو پرتابگر وزنه در یک مسابقهٔ ورزشی، وزنه های خود را با زاویه های متفاوت α و b که α<b است، پرتاب کرده اند. پرتابگر A، زاویه α را انتخاب می کند و مسیر طی شده از رابطۀ \(y = - \frac{{{x^2}}}{2} + \frac{3}{2}x + 2\) به دست می آید. پرتابگر B نیز زاویۀ b را انتخاب می کند و مسیر طی شده از رابطهٔ \(y = - 2{x^2} + 3x + 2\) به دست می آید. در هر دو معادله، y ارتفاع وزنه از سطح زمین و x مسافت افقی طی شده، بر حسب متر است.
الف مسیر حرکت هر کدام از وزنه ها را رسم کنید.
ب محل برخورد وزنه ها با زمین یا محور xها درچه نقاطی است؟ کدام یک از وزنه ها مسافت افقی بیشتری را طی کرده است؟
پ کدام یک از وزنه ها ارتفاع بیشتری از سطح زمین پیدا کرده است؟ اندازهٔ آنها را مشخص کنید.
الف
مسیر پرتابه A:
\(\begin{array}{*{20}{l}}{y = - \frac{{{x^2}}}{2} + \frac{3}{2}x + 2 = - \frac{1}{2}{{\left( {x - \frac{3}{2}} \right)}^2} + \frac{{25}}{8}}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = \frac{3}{2}}\\{{y_0} = \frac{{25}}{8}}\end{array}} \right.\;\;{\mkern 1mu} {\kern 1pt} ,\;\;{\mkern 1mu} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}}{{x_1} = \frac{1}{2}}\\{{y_1} = \frac{{21}}{8}}\end{array}} \right.\;\;{\mkern 1mu} {\kern 1pt} ,\;\;{\mkern 1mu} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}}{{x_2} = \frac{3}{2}}\\{{y_2} = \frac{{21}}{8}}\end{array}} \right.}\end{array}\)
مسیر پرتابه B:
\(\begin{array}{*{20}{l}}{y = - 2{x^2} + 3x + 2 = - 2{{\left( {x - \frac{3}{4}} \right)}^2} + \frac{{25}}{8}}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = \frac{3}{4}}\\{{y_0} = \frac{{25}}{8}}\end{array}} \right.\;\;{\mkern 1mu} {\kern 1pt} ,\;\;{\mkern 1mu} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}}{{x_1} = - \frac{1}{4}}\\{{y_1} = \frac{9}{8}}\end{array}} \right.\;\;{\mkern 1mu} {\kern 1pt} ,\;\;{\mkern 1mu} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}}{{x_2} = \frac{7}{4}}\\{{y_2} = \frac{9}{8}}\end{array}} \right.}\end{array}\)
ب
طول های برخورد پرتابه A با زمین:
\(\begin{array}{*{20}{l}}{ - \frac{{{x^2}}}{2} + \frac{3}{2}x + 2 = - \frac{1}{2}{{\left( {x - \frac{3}{2}} \right)}^2} + \frac{{25}}{8} = 0}\\{ \Rightarrow \frac{1}{2}{{\left( {x - \frac{3}{2}} \right)}^2} = \frac{{25}}{8} \Rightarrow {{\left( {x - \frac{3}{2}} \right)}^2} = \frac{{25}}{4}}\\{ \Rightarrow x - \frac{3}{2} = \pm \frac{5}{2} \Rightarrow x = \frac{3}{2} \pm \frac{5}{2} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = - 1}\\{{x_2} = 4}\end{array}} \right.}\\{}\\{ \Rightarrow \Delta {x_A} = {x_2} - {x_1} = 4 + 1 = 5}\end{array}\)
طول های برخورد پرتابه B با زمین:
\(\begin{array}{*{20}{l}}{ - 2{x^2} + 3x + 2 = - 2{{\left( {x - \frac{3}{4}} \right)}^2} + \frac{{25}}{8} = 0}\\{ \Rightarrow 2{{\left( {x - \frac{3}{4}} \right)}^2} = \frac{{25}}{8} \Rightarrow {{\left( {x - \frac{3}{4}} \right)}^2} = \frac{{25}}{{16}}}\\{ \Rightarrow x - \frac{3}{4} = \pm \frac{5}{4} \Rightarrow x = \frac{3}{4} \pm \frac{5}{4} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} = - \frac{1}{4}}\\{{x_2} = 2}\end{array}} \right.}\\{ \Rightarrow \Delta {x_B} = {x_2} - {x_1} = 2 + \frac{1}{4} = \frac{9}{4}}\end{array}\)
پرتابه A مسیر افقی بیشتری رفته است:
\(\Delta {x_B} < \Delta {x_A}\)
پ
میزان ارتفاع همان عرض نقطه سهمی است که در این مورد هر دو عرض یکسان است، پس ارتفاع یکسانی پیموده اند؛ یعنی ارتفاع پیموده شده آنها \(\frac{{25}}{8}\) است.
گام به گام کتاب های پایه دهم
گام به گام جامع کتاب ریاضی دهم
گام به گام جامع کتاب شیمی دهم
گام به گام جامع کتاب فارسی دهم
گام به گام جامع کتاب نگارش دهم
گام به گام جامع کتاب عربی دهم
گام به گام جامع کتاب زبان انگلیسی دهم
گام به گام جامع کتاب کتاب کار انگلیسی دهم
گام به گام جامع کتاب آمادگی دفاعی دهم
گام به گام جامع کتاب دین و زندگی دهم
گام به گام جامع کتاب جغرافیای ایران دهم
گام به گام جامع کتاب آزمایشگاه علوم تجربی دهم
گام به گام جامع کتاب تفکر و سواد رسانه ای دهم
گام به گام جامع کتاب کارگاه کارآفرینی و تولید
فعالیت صفحه 84 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ فعالیت صفحه 84 درس 4
جواب فعالیت صفحه 84 درس 4 ریاضی دهم
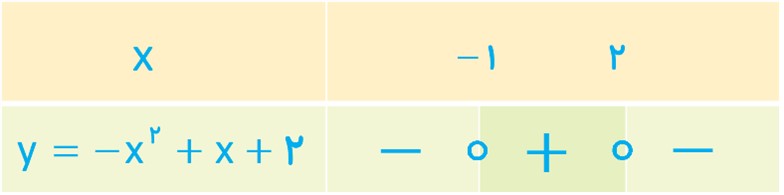
1 نمودار خط y=2x-6 در شکل مقابل رسم شده است. با استفاده از آن، علامت y را در جدول زیر بنویسید.
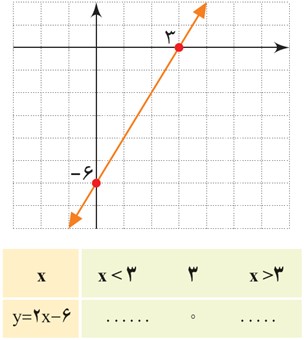
2 نمودار خط y=-2x+6 را در شکل مقابل رسم کنید و جدول زیر که علامت y را برای xهای مختلف تعیین می کند، کامل کنید.
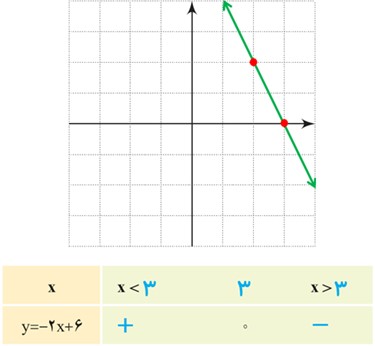
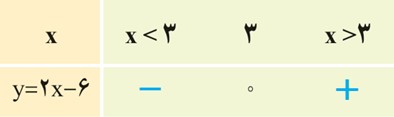
3 در دو قسمت بالا علامت عددی که ضریب x است، چه تفاوتی در جدول تعیین علامت این خطوط ایجاد کرده است؟
اگر ضریب x مثبت باشد، علامت قبل از ریشه منفی و بعد از آن مثبت است، اگر ضریب x منفی شود، علامت ها عکس خواهد شد، یعنی قبل از ریشه مثبت و بعد از آن منفی خواهد شد.
4 نشان دهید که علامت عبارت y=ax+b ، برای xهای مختلف از جدول زیر تعیین می شود.

اگر a مثبت باشد، حالت نمودار به شکل زیر خواهد بود. با توجه به شکل قبل از ریشه منفی و بعد از ریشه مثبت است، یعنی قبل از ریشه، مخالف علامت a است و بعد از ریشه، موافق علامت a است؛ یعنی:
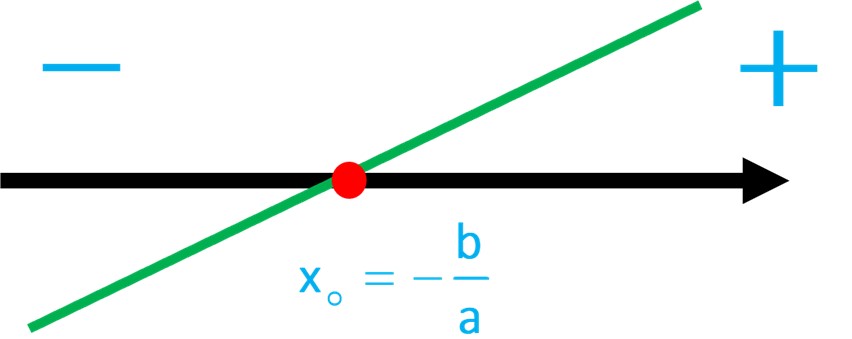
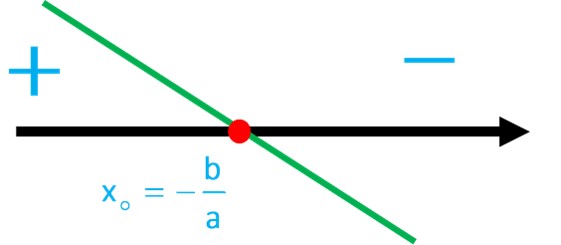
اگر a منفی باشد، حالت نمودار به شکل زیر خواهد بود. با توجه به شکل قبل از ریشه مثبت و بعد از ریشه منفی است، یعنی قبل از ریشه، مخالف علامت a است و بعد از ریشه، موافق علامت a است؛ یعنی:
مثال صفحه 84 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ مثال صفحه 84 درس 4
جواب مثال صفحه 84 درس 4 ریاضی دهم
عبارت y=5x-4 را تعیین علامت می کنیم.
ریشۀ عبارت 5x-2 از معادلۀ 5x-2=0 به دست می آید که برابر \(x = \frac{2}{5}\) است.
با توجه به اینکه علامت ضریب x ؛ یعنی a=5، مثبت است، طبق جدول بالا، جدول تعیین علامت به صورت زیر است:
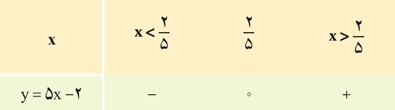
مقدار y را برای x=3 و x=-1 به دست آورید و صحت علامت اعداد به دست آمده را با جدول بالا بررسی کنید.
\(x = - 1 \Rightarrow y = 5\left( { - 1} \right) - 2 = - 5 - 2 = - 7 \to \)منفی:
\(x = 3\,\,{\kern 1pt} \Rightarrow y = 5\left( 3 \right) - 2 = 15 - 2 = 13\;\;{\mkern 1mu} {\kern 1pt} \to \)مثبت:
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
مثال صفحه 85 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ مثال صفحه 85 درس 4
جواب مثال صفحه 85 درس 4 ریاضی دهم
علامت عبارت A = (2x-1)(3-x) را برای xهای مختلف تعیین می کنیم.
جدول تعیین علامت برای هرکدام از عبارت های 3-x و 2x-1 به صورت زیراست:
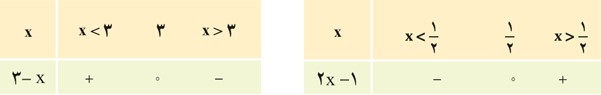
اطلاعات این دو جدول را در یک جدول به صورت زیر می نویسیم:

بنابراین در سه ناحیهٔ بالا که با رنگ های مختلف نشان داده شده، علامت هرکدام از این دو عبارت مشخص شده است. مثلاً برای x>3، عبارت 2x-1، مثبت است؛ ولی 3-x منفی می باشد، پس علامت عبارت حاصل ضرب آنها، منفی خواهد بود. با بحث مشابه، برای دو ناحیهٔ دیگر، جدول تعیین علامت A = (2x-1)(3-x) به صورت زیر است.
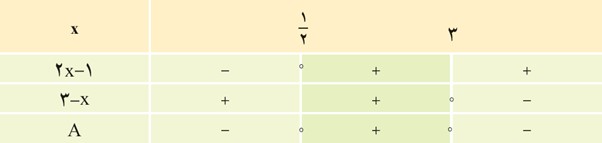
دقت کنید که روی ستون ها نیز قاعدهٔ ضرب انجام شده است.
مقدار A را برای x=4 و x=0 به دست آورید و صحت علامت مقادیر به دست آمده را با جدول بالا بررسی کنید.
\(x = 0\,\,\, \Rightarrow \,\,y = \left( {2\left( 0 \right) - 1} \right)\left( {3 - \left( 0 \right)} \right) = \left( { - 1} \right)\left( 3 \right) = - 3 \to \)منفی:
\(x = 4 \Rightarrow y = \left( {2\left( 4 \right) - 1} \right)\left( {3 - \left( 4 \right)} \right) = \left( 7 \right)\left( { - 1} \right) = - 7 \to \)مثبت:
گام به گام کتاب های پایه دهم
گام به گام جامع کتاب ریاضی دهم
گام به گام جامع کتاب شیمی دهم
گام به گام جامع کتاب فارسی دهم
گام به گام جامع کتاب نگارش دهم
گام به گام جامع کتاب عربی دهم
گام به گام جامع کتاب زبان انگلیسی دهم
گام به گام جامع کتاب کتاب کار انگلیسی دهم
گام به گام جامع کتاب آمادگی دفاعی دهم
گام به گام جامع کتاب دین و زندگی دهم
گام به گام جامع کتاب جغرافیای ایران دهم
گام به گام جامع کتاب آزمایشگاه علوم تجربی دهم
گام به گام جامع کتاب تفکر و سواد رسانه ای دهم
گام به گام جامع کتاب کارگاه کارآفرینی و تولید
کاردرکلاس صفحه 85 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ کاردرکلاس صفحه 85 درس 4
جواب کاردرکلاس صفحه 85 درس 4 ریاضی دهم
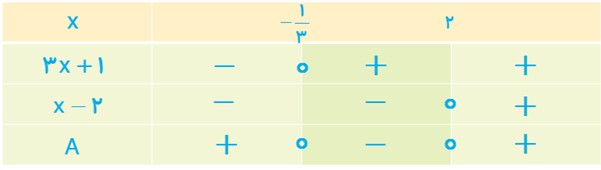
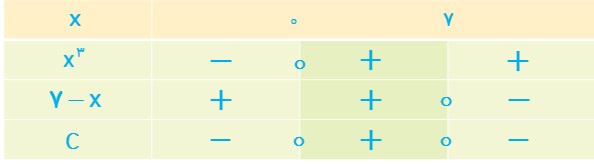
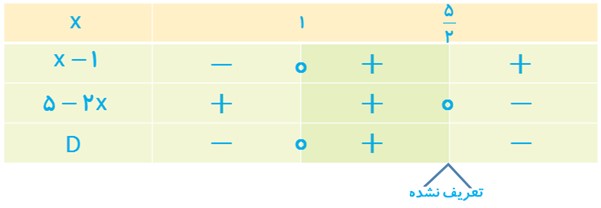
هریک از عبارت های زیر را تعیین علامت کنید.
الف \(A = \left( {3x + 1} \right)\left( {x - 2} \right)\)
ب \(B = {\left( {2x - 3} \right)^2}\)
پ \(C = {x^2}\left( {7 - x} \right)\)
ت \(D = \frac{{x - 1}}{{5 - 2x}}\)
الف
ب

پ
ت
فعالیت صفحه 86 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ فعالیت صفحه 86 درس 4
جواب فعالیت صفحه 86 درس 4 ریاضی دهم
1 فرض کنید که معادلهٔ P(x)=0، دو ریشه متمایز x1 و x2 (x1<x2) داشته و به شکل \(P\left( x \right) = a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\) تجزیه شده باشد. با تکمیل جدول زیر، علامت P(x) را برای xهای مختلف تعیین کنید.
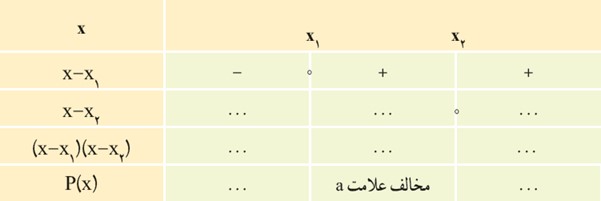

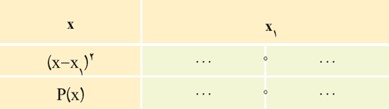
2 اگر معادلهٔ P(x)=0 ریشهٔ مضاعف برابر با x1 داشته باشد، می توانیم P(x) را به شکل\(P\left( x \right) = a{\left( {x - {x_1}} \right)^2}\) بنویسیم. با تکمیل جدول زیر، علامت P(x) را برای xهای مختلف تعیین کنید.

3 اکنون فرض کنید \(\Delta < 0\) باشد، در این صورت معادلهٔ P(x)=0 ریشهٔ حقیقی ندارد. با توجه به اینکه \(P\left( x \right) = a\left[ {{{\left( {x + \frac{b}{{2a}}} \right)}^2} - \frac{\Delta }{{4{a^2}}}} \right]\) علامت P(x) را در جدول زیر تعیین کنید.


4 با توجه به قسمت بالا، مشخص کنید اگر P(x) برای هر \(x \in R\) مثبت باشد، a و \(\Delta\) چه علامتی دارند؟ برای وقتی که P(x) منفی است، نیز علامت a و \(\Delta\) را تعیین کنید.
\(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{a > 0}\\{\Delta < 0}\end{array}} \right. \Rightarrow P\left( x \right) > 0}\\{}\\{\left\{ {\begin{array}{*{20}{l}}{a < 0}\\{\Delta < 0}\end{array}} \right. \Rightarrow P\left( x \right) < 0}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
کاردرکلاس صفحه 88 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ کاردرکلاس صفحه 88 درس 4
جواب کاردرکلاس صفحه 88 درس 4 ریاضی دهم
1 چندجمله ای \(y = - {x^2} + x + 2\) را با محاسبهٔ ریشه ها، در یک جدول تعیین علامت کنید؛ سپس با رسم آن، صحت علامت های به دست آمده در جدول را با نمودار، بررسی کنید.
\(\begin{array}{*{20}{l}}{y = - {x^2} + x + 2}\\\begin{array}{l} - {x^2} + x + 2 = 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 1}\\{b = 1}\\{c = 2}\end{array}} \right. \Rightarrow \Delta = {b^2} - 4ac = {\left( 1 \right)^2} - 4\left( { - 1} \right)\left( 2 \right) = 9\\\end{array}\\\begin{array}{l}x = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{ - 1 \pm 3}}{{ - 2}}\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}{x_1} = \frac{{ - 1 + 3}}{{ - 2}} = - 1\\\end{array}\\{{x_2} = \frac{{ - 1 - 3}}{{ - 2}} = 2}\end{array}} \right.\end{array}\end{array}\)
\(x^\circ = \frac{{ - 1 + 2}}{2} = \frac{1}{2} \Rightarrow y^\circ = \frac{9}{8}\,\, \Rightarrow \left( {\frac{1}{2}\,,\,\frac{9}{8}} \right)\)
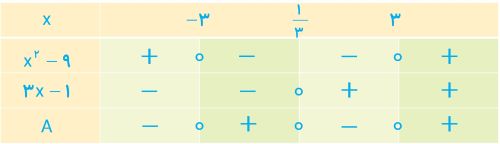
2 عبارت های زیر را تعیین علامت کنید.
الف \(A = \left( {{x^2} - 9} \right)\left( {3x - 1} \right)\)
ب \(B = \frac{{ - {x^2} + 6x - 9}}{{{x^2} + x + 3}}\)
الف
\(\left\{ {\begin{array}{*{20}{l}}{{x^2} - 9 = 0 \Rightarrow \left( {x - 3} \right)\left( {x + 3} \right) = 0 \Rightarrow x = - 3\,\,,\,\,x = 3}\\{3x - 1 = 0 \Rightarrow x = \frac{1}{3}}\end{array}} \right.\)
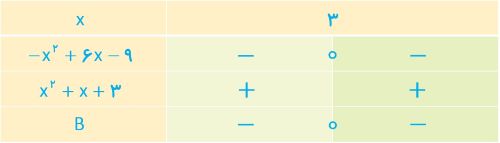
ب
\(\left\{ {\begin{array}{*{20}{l}}{ - {x^2} + 6x - 9 = 0 \Rightarrow - {{\left( {x - 3} \right)}^2} = 0 \Rightarrow x = 3}\\{{x^2} + x + 3 = 0 \Rightarrow \Delta = {{\left( 1 \right)}^2} - 4\left( 1 \right)\left( 3 \right) = - 11 < 0\,\, \otimes }\end{array}} \right.\)
گام به گام کتاب های پایه دهم
گام به گام جامع کتاب ریاضی دهم
گام به گام جامع کتاب شیمی دهم
گام به گام جامع کتاب فارسی دهم
گام به گام جامع کتاب نگارش دهم
گام به گام جامع کتاب عربی دهم
گام به گام جامع کتاب زبان انگلیسی دهم
گام به گام جامع کتاب کتاب کار انگلیسی دهم
گام به گام جامع کتاب آمادگی دفاعی دهم
گام به گام جامع کتاب دین و زندگی دهم
گام به گام جامع کتاب جغرافیای ایران دهم
گام به گام جامع کتاب آزمایشگاه علوم تجربی دهم
گام به گام جامع کتاب تفکر و سواد رسانه ای دهم
گام به گام جامع کتاب کارگاه کارآفرینی و تولید
فعالیت صفحه 89 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ فعالیت صفحه 89 درس 4
جواب فعالیت صفحه 89 درس 4 ریاضی دهم
فرض کنید x متغیری باشد که همزمان در دو نامعادلهٔ زیر صدق می کند:
\( - 2 < 3x - 1\;\;,\;\;3x - 1 \le 8\)
1
الف هر کدام از نامعادله های بالا را حل کنید و مجموعه جواب های به دست آمده را روی محور مقابل آنها رسم کنید.
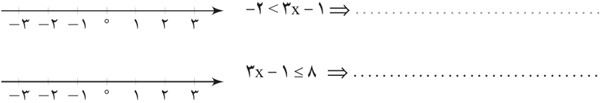
ب به خاطر وجود «و» بین دو نامعادله، اشتراک مجموعه جواب های به دست آمده را مشخص و آن را روی محور مقابل رسم کنید.

الف
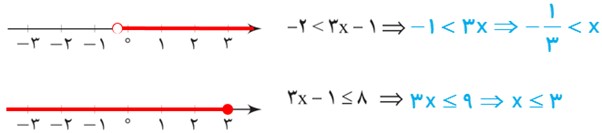
ب
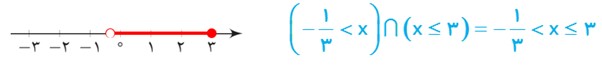
2 می توانیم دو نامعادلهٔ فوق را ترکیب کنیم و به شکل یک نامعادلهٔ دوگانه به صورت \( - 2 < 3x - 1 \le 8\) بنویسیم. از خواص جمع و ضرب نامساوی ها استفاده کنید و این نامعادلهٔ دوگانه را حل کنید:
\( - 2 < 3x - 1 \le 8\) به دو نامعادله 1+ را اضافه می کنیم
\(.... < 3x \le 9\) دو نامعادله را در \(\frac{1}{3}\) ضرب می کنیم
\(.... < x \le ....\)
جواب به دست آمده از این روش را با جوابی که در قسمت بالا به آن رسیده اید، مقایسه کنید. نامعادلهٔ دوگانهٔ فوق را به صورت دستگاه نامعادله های زیر نیز نشان می دهیم:
\(\left\{ \begin{array}{l}3x - 1 > - 2\\3x - 1 \le 8\end{array} \right.\)
\( - 1 < 3x \le 9\) دو نامعادله را در \(\frac{1}{3}\) ضرب می کنیم
\( - \frac{1}{3} < x \le 3\)
کاردرکلاس صفحه 90 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ کاردرکلاس صفحه 90 درس 4
جواب کاردرکلاس صفحه 90 درس 4 ریاضی دهم
حداقل و حداکثر دمای یک شهر در یک روز، ١٥ و ٢٥ درجهٔ سانتی گراد و رابطه ای که درجهٔ فارنهایت (F) را به سانتی گراد (C) تبدیل می کند، به صورت \(C = \frac{5}{9}\left( {F - 32} \right)\) است. حداقل و حداکثر دمای این شهر را برحسب فارنهایت تعیین کنید. (قرار دهید \(15 \le C \le 25\) ؛ سپس از رابطۀ داده شده، C را بر حسب F بنویسید و نامعادلهٔ دوگانهٔ به دست آمده را حل کنید.)
\(\begin{array}{*{20}{l}}\begin{array}{l}15 \le C \le 25 \Rightarrow 15 \le \frac{5}{9}\left( {F - 32} \right) \le 25\\\\ \Rightarrow \frac{9}{5} \times 15 \le F - 32 \le \frac{9}{5} \times 25\end{array}\\\begin{array}{l}\\ \Rightarrow 27 \le F - 32 \le 45\\\\ \Rightarrow 27 + 32 \le F \le 45 + 32 \Rightarrow 59 \le F \le 77\end{array}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
فعالیت صفحه 90 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ فعالیت صفحه 90 درس 4
جواب فعالیت صفحه 90 درس 4 ریاضی دهم
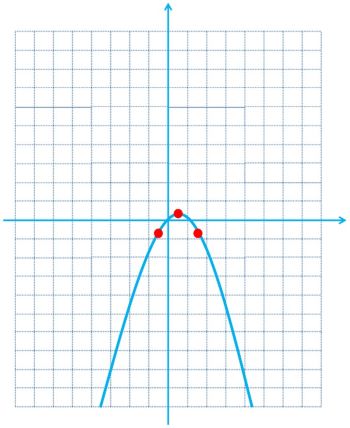
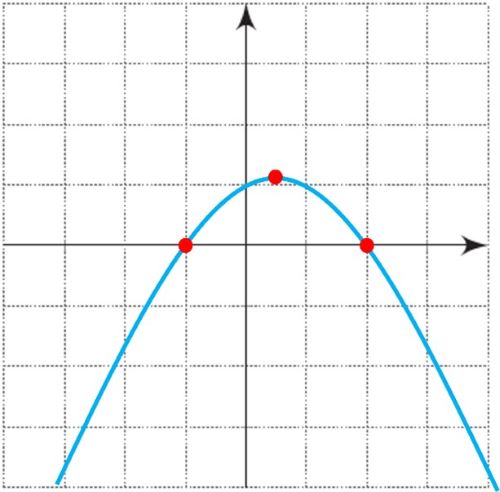
سهمی \(y = {x^2} - 2x - 3\) را درنظر بگیرید که نمودار آن در شکل مقابل رسم شده است.
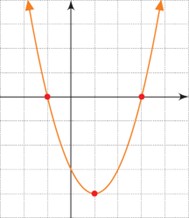
الف به کمک نمودار رسم شده، برای چه مقادیری از x، نمودار سهمی، پایین محور xهاست؟
ب جدول تعیین علامت عبارت \(y = {x^2} - 2x - 3\) را رسم کنید و مشخص کنید برای چه مقادیری از x ، علامت y منفی است؟
پ نشان دهید که از مجموعه جواب های به دست آمده در هر یک از قسمت های الف و ب می توان برای حل نامعادلهٔ \({x^2} - 2x - 3 < 0\) استفاده کرد.
الف
\(-1 < x < 3\)
ب
\(y = {x^2} - 2x - 3 = \left( {x + 1} \right)\left( {x - 3} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x + 1 = 0 \Rightarrow x = - 1}\\{x - 3 = 0 \Rightarrow x = 3}\end{array}} \right.\)
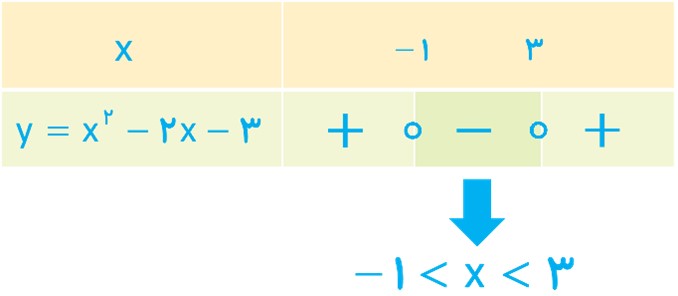
پ
\({x^2} - 2x - 3 < 0\) یعنی مجموعه مقادیری از x که به ازای آن ها 0>y باشد که با توجه به نمودار
-1 < x < 3 مشخص شده است. همچنین به کمک جدول تعیین علامت نیز به همین جواب رسیدیم.
گام به گام کتاب های پایه دهم
گام به گام جامع کتاب ریاضی دهم
گام به گام جامع کتاب شیمی دهم
گام به گام جامع کتاب فارسی دهم
گام به گام جامع کتاب نگارش دهم
گام به گام جامع کتاب عربی دهم
گام به گام جامع کتاب زبان انگلیسی دهم
گام به گام جامع کتاب کتاب کار انگلیسی دهم
گام به گام جامع کتاب آمادگی دفاعی دهم
گام به گام جامع کتاب دین و زندگی دهم
گام به گام جامع کتاب جغرافیای ایران دهم
گام به گام جامع کتاب آزمایشگاه علوم تجربی دهم
گام به گام جامع کتاب تفکر و سواد رسانه ای دهم
گام به گام جامع کتاب کارگاه کارآفرینی و تولید
کاردرکلاس صفحه 90 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ کاردرکلاس صفحه 90 درس 4
جواب کاردرکلاس صفحه 90 درس 4 ریاضی دهم
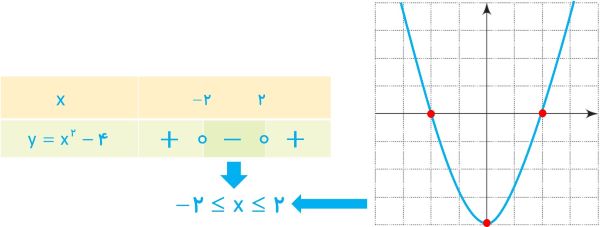
هریک از نامعادلات زیر را به دو روش هندسی و جدول تعیین علامت، حل کنید.
الف \({x^2} \le 4\)
ب \(3{x^2} - x - 2 \ge 0\)
الف
\(\begin{array}{*{20}{l}}{{x^2} \le 4 \Rightarrow {x^2} - 4 \le 0}\\{{x^2} - 4 = 0 \Rightarrow {x^2} = 4 \Rightarrow x = \pm 2}\end{array}\)
ب
\(\begin{array}{*{20}{l}}{3{x^2} - x - 2 \ge 0}\\{3{x^2} - x - 2 = 0 \Rightarrow \Delta = {{\left( { - 1} \right)}^2} - 4\left( 3 \right)\left( { - 2} \right) = 25}\\{x = \frac{{ - \left( { - 1} \right) \pm \sqrt {25} }}{{2\left( 3 \right)}} = \frac{{1 \pm 5}}{6} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = - \frac{2}{3}}\\{x = 1}\end{array}} \right.}\end{array}\)

فعالیت صفحه 91 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ فعالیت صفحه 91 درس 4
جواب فعالیت صفحه 91 درس 4 ریاضی دهم
1 نامعادلهٔ \(\left| x \right| \le 3\) رادرنظر بگیرید. مجموعه جواب این نامعادله، شامل اعداد حقیقی x است که فاصلهٔ آنها از مبدأ کوچک تر یا مساوی باشد. این اعداد را روی محور زیر نمایش دهید.

مجموعهٔ مقادیری را که در نمودار بالا مشخص کرده اید، به صورت بازه بنویسید.

\(x \in \left[ { - 3\,,\,3} \right]\)
2 نامعادلۀ \(\left| x \right| \ge 3\) را درنظر بگیرید. مجموعه جواب این نامعادله، شامل اعداد حقیقی x است که فاصلهٔ آنها از مبدأ بزرگ تر یا مساوی ٣ باشند، این اعداد را روی محور زیر نشان دهید.

مجموعهٔ این مقادیر را که در نمودار بالا مشخص کرده اید، به صورت بازه بنویسید.

\(x \in ( - \infty ,\; - 3]\; \cup \;[3\;,\; + \infty )\)
3 با استفاده از مراحل بالا، جاهای خالی را با عبارت های مناسب پرکنید.


مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دهم- آزمون آنلاین تمامی دروس پایه دهم
- گام به گام تمامی دروس پایه دهم
- ویدئو های آموزشی تمامی دروس پایه دهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دهم
- فلش کارت های آماده دروس پایه دهم
- گنجینه ای جامع از انشاء های آماده پایه دهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دهم
کاردرکلاس صفحه 93 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ کاردرکلاس صفحه 93 درس 4
جواب کاردرکلاس صفحه 93 درس 4 ریاضی دهم
1 در هریک از نامعادله های زیر، مجموعه جواب را با نماد بازه به دست آورید؛ سپس آن را روی محور نشان دهید.
الف \(\left| {\frac{x}{3} + 1} \right| < \frac{2}{3}\)
ب \(\left| {5 - 2x} \right| \ge 1\)
الف
\(\begin{array}{l}\left| {\frac{x}{3} + 1} \right| < \frac{2}{3} \Rightarrow \left| {\frac{{x + 3}}{3}} \right| < \frac{2}{3}\\\\ \Rightarrow \left| {x + 3} \right| < 2\\\\ \Rightarrow - 2 < x + 3 < 2 \Rightarrow - 5 < x < - 1\\\\ \Rightarrow x \in \left( { - 5\,,\, - 1} \right)\end{array}\)

ب
\(\begin{array}{l}\left| {5 - 2x} \right| \ge 1 \Rightarrow \left| {2x - 5} \right| \ge 1\\\\ \Rightarrow - 1 \le 2x - 5 \le 1 \Rightarrow 4 \le 2x \le 6\\\\ \Rightarrow 2 \le x \le 3 \Rightarrow x \in \left[ {2\,,\,3} \right]\end{array}\)

2 یک نامعادلهٔ قدر مطلقی بنویسید که مجموعه جواب آن بازهٔ (1,9) باشد.
\(\begin{array}{*{20}{l}}{x \in \left( {a\,,\,b} \right) \Leftrightarrow \left| {x - r} \right| < d \Rightarrow \left\{ {\begin{array}{*{20}{l}}{r = \frac{{a + b}}{2}}\\{d = \frac{{b - a}}{2}}\end{array}} \right.}\\{ \Rightarrow x \in \left( {1\,,\,9} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{r = \frac{{9 + 1}}{2} = \frac{{10}}{2} = 5}\\{d = \frac{{9 - 1}}{2} = \frac{8}{2} = 4}\end{array}} \right. \Rightarrow \left| {x - 5} \right| < 4}\end{array}\)
3 یک نامعادلهٔ قدر مطلقی بنویسید که مجموعه جواب آن \(\left( { - \infty ,3} \right] \cup \left[ {6, + \infty } \right)\) باشد.
\(\begin{array}{*{20}{l}}{x \in \left( {\left. { - \infty \,,\,a} \right]} \right. \cup \left[ {\left. {b\,,\,\infty } \right)} \right. \Leftrightarrow \left| {x - r} \right| > d \Rightarrow \left\{ {\begin{array}{*{20}{l}}{r = \frac{{a + b}}{2}}\\{d = \frac{{b - a}}{2}}\end{array}} \right.}\\{ \Rightarrow x \in \left( {\left. { - \infty \,,\,3} \right]} \right. \cup \left[ {\left. {6\,,\,\infty } \right)} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{r = \frac{{6 + 3}}{2} = \frac{9}{2}}\\{d = \frac{{6 - 3}}{2} = \frac{3}{2}}\end{array}} \right. \Rightarrow \left| {x - \frac{9}{2}} \right| > \frac{3}{2}}\end{array}\)
گام به گام کتاب های پایه دهم
گام به گام جامع کتاب ریاضی دهم
گام به گام جامع کتاب شیمی دهم
گام به گام جامع کتاب فارسی دهم
گام به گام جامع کتاب نگارش دهم
گام به گام جامع کتاب عربی دهم
گام به گام جامع کتاب زبان انگلیسی دهم
گام به گام جامع کتاب کتاب کار انگلیسی دهم
گام به گام جامع کتاب آمادگی دفاعی دهم
گام به گام جامع کتاب دین و زندگی دهم
گام به گام جامع کتاب جغرافیای ایران دهم
گام به گام جامع کتاب آزمایشگاه علوم تجربی دهم
گام به گام جامع کتاب تفکر و سواد رسانه ای دهم
گام به گام جامع کتاب کارگاه کارآفرینی و تولید
تمرین صفحه 93 درس معادله ها و نامعادله ها ریاضی دهم
پاسخ تمرین صفحه 93 درس 4
جواب تمرین صفحه 93 درس 4 ریاضی دهم
1 در هریک از نامعادله های زیر، مجموعه جواب را به شکل بازه بنویسید.
الف \(1 < 2x - 3 \le 3\)
ب \(x + 1 \le 5 - x < 2x + 3\)
پ \( - 2 < \frac{{5 - x}}{2} < 0\)
ت \(\frac{{4 - 2x}}{{3x + 1}} \ge 0\)
ث \(x\left( {{x^2} + 4} \right) < 0\)
ج \(\frac{{{x^3} - x}}{{{x^2} - 2x + 2}} \le 0\)
چ \(\left| {7 - 2x} \right| < 1\)
ح \(\left| {\frac{{x - 1}}{2} - 1} \right| \ge 3\)
الف
\(1 < 2x - 3 \le 3 \Rightarrow 4 < 2x \le 6 \Rightarrow 2 < x \le 3 \Rightarrow x \in \left( {\left. {2\,,\,3} \right]} \right.\)
ب
\(\begin{array}{*{20}{l}}\begin{array}{l}x + 1 \le 5 - x < 2x + 3\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x + 1 \le 5 - x \Rightarrow 2x \le 4 \Rightarrow x \le 2 \Rightarrow x \in \left( {\left. { - \infty \,,\,2} \right]} \right.\\\end{array}\\{5 - x < 2x + 3 \Rightarrow 2 < 3x \Rightarrow \frac{2}{3} < x \Rightarrow x \in \left( {\frac{2}{3}\,,\,\infty } \right)}\end{array}} \right.\end{array}\\{}\\{ \Rightarrow x \in \left( {\left. { - \infty \,,\,2} \right]} \right. \cap \left( {\frac{2}{3}\,,\,\infty } \right) \Rightarrow x \in \left( {\left. {\frac{2}{3}\,,\,2} \right]} \right.}\end{array}\)
پ
\(\begin{array}{l} - 2 < \frac{{5 - x}}{2} < 0\,\mathop {\, \Rightarrow }\limits^{ \times \left( { - 1} \right)} \,\,0 < \frac{{x - 5}}{2} < 2\\\\ \Rightarrow 0 < x - 5 < 4 \Rightarrow 5 < x < 9 \Rightarrow x \in \left( {5\,,\,9} \right)\end{array}\)
ت
\(A = \frac{{4 - 2x}}{{3x + 1}} \ge 0\,\,\, \Rightarrow \left\{ {\begin{array}{*{20}{l}}{4 - 2x = 0 \Rightarrow x = 2}\\{3x + 1 = 0 \Rightarrow x = - \frac{1}{3}}\end{array}} \right.\)
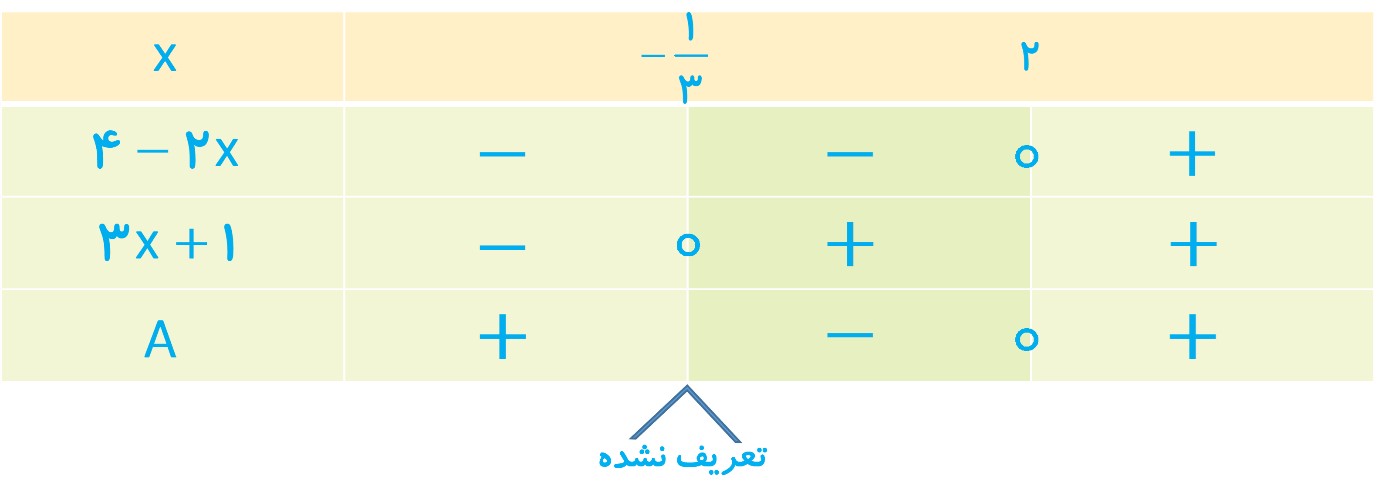
\(x \in ( - \infty \,,\, - \frac{1}{3}) \cup \left[ {\left. {2\,,\,\infty } \right)} \right.\)
ث
\(B = x\left( {{x^2} + 4} \right) < 0\,\, \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} + 4 = 0 \Rightarrow \Delta = {{\left( 0 \right)}^2} - 4\left( 1 \right)\left( 4 \right) = - 16 < 0}\end{array}} \right.\)
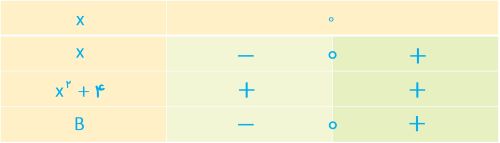
\(x \in \left( { - \infty {\kern 1pt} ,\,0} \right)\)
ج
\(\begin{array}{*{20}{l}}{C = \frac{{{x^3} - x}}{{{x^2} - 2x + 2}} = \frac{{x\left( {{x^2} - 1} \right)}}{{{x^2} - 2x + 2}} \le 0}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} - 1 = 0 \Rightarrow {x^2} = 1 \Rightarrow x = \pm 1}\\{{x^2} - 2x + 2 = 0 \Rightarrow \Delta = {{\left( { - 2} \right)}^2} - 4\left( 1 \right)\left( 2 \right) = - 4 < 0}\end{array}} \right.}\end{array}\)
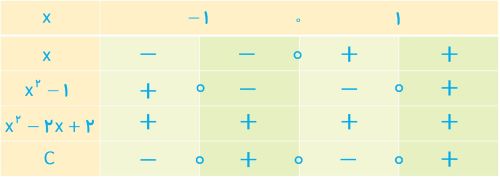
\(x \in \left( {\left. { - \infty {\kern 1pt} ,\, - 1} \right]} \right. \cup \left[ {0\,,\,1} \right]\)
چ
\(\begin{array}{l}\left| {7 - 2x} \right| < 1 \Rightarrow \left| {2x - 7} \right| < 1 \Rightarrow - 1 < 2x - 7 < 1\\\\ \Rightarrow 6 < 2x < 8 \Rightarrow 3 < x < 4 \Rightarrow x \in \left( {3\,,\,4} \right)\end{array}\)
ح
\(\begin{array}{*{20}{l}}\begin{array}{l}\left| {\frac{{x - 1}}{2} - 1} \right| \ge 3 \Rightarrow \left| {\frac{{x - 3}}{2}} \right| \ge 3 \Rightarrow \left| {x - 3} \right| \ge 6\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x - 3 > 6 \Rightarrow x > 9 \Rightarrow x \in \left( {9\,,\,\infty } \right)\\\end{array}\\{x - 3 < - 6 \Rightarrow x < - 3 \Rightarrow x \in \left( { - \infty \,,\, - 3} \right)}\end{array}} \right.\\\end{array}\\{x \in \left( { - \infty \,,\, - 3} \right) \cup \left( {9\,,\,\infty } \right)}\end{array}\)
2 به ازای چه مقادیری از k ، عبارت \(A = {x^2} + 3x + k\) همواره مثبت است؟
\(\begin{array}{*{20}{l}}{A = {x^2} + 3x + k}\\{\forall x \in \mathbb{R}:A > 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1 > 0}\\{\Delta < 0}\end{array}} \right.}\\{\Delta < 0 \Rightarrow {b^2} - 4ac > 0 \Rightarrow {{\left( 3 \right)}^2} - 4\left( 1 \right)\left( k \right) < 0}\\{ \Rightarrow 9 - 4k < 0 \Rightarrow k > \frac{9}{4}}\end{array}\)
3 به ازای چه مقادیری از m، سهمی \(y = m{x^2} - mx - 1\) همواره پایین محور xهاست؟
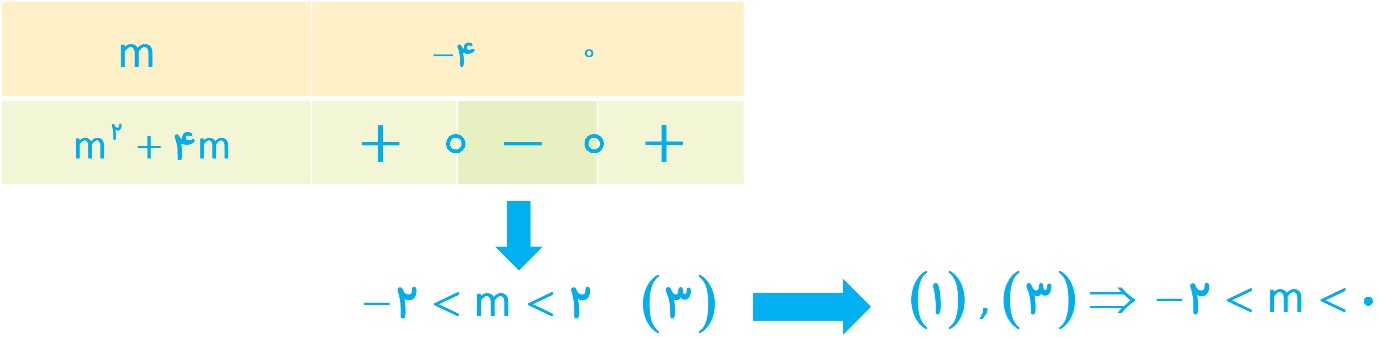
\(\begin{array}{l}y = m{x^2} - mx - 1\\\\\forall x \in \mathbb{R}:y < 0\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}a < 0 \Rightarrow m < 0\;\;{\mkern 1mu} {\kern 1pt} \left( 1 \right)\\\end{array}\\{\Delta < 0 \Rightarrow {b^2} - 4ac < 0 \Rightarrow {m^2} + 4m < 0\;\;{\mkern 1mu} {\kern 1pt} \left( 2 \right)}\end{array}} \right.\\\\\left( 2 \right):\\\\{m^2} + 4m < 0 \Rightarrow {m^2} + 4m = 0\\\\ \Rightarrow m\left( {m + 4} \right) = 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}m = 0\\\end{array}\\{m = - 4}\end{array}} \right.\end{array}\)
4 یک جسم از بالای یک ساختمان که ١٣ متر ارتفاع دارد، به هوا پرتاب می شود. اگر ارتفاع این جسم از سطح زمین در ثانیهٔ t از رابطۀ \(h = - 5{t^2} + 18t + 13\) محاسبه شود، در چه فاصلهٔ زمانی، ارتفاع توپ از سطح زمین بیشتر از ١٣ متر خواهد بود؟
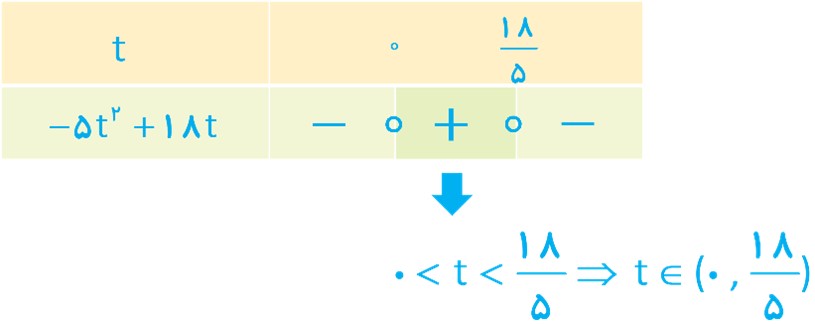
\(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{h = - 5{t^2} + 18t + 13}\\{h > 13 \Rightarrow t \in \left( {{t_1}\,,\,{t_2}} \right)}\end{array}} \right. \Rightarrow {t_1},{t_2} = ?}\\{ - 5{t^2} + 18t + 13 > 13 \Rightarrow - 5{t^2} + 18t > 0}\\{ \Rightarrow - 5{t^2} + 18t = 0 \Rightarrow t\left( { - 5t + 18} \right) = 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{t_1} = 0}\\{ - 5t + 18 = 0 \Rightarrow {t_2} = \frac{{18}}{5}}\end{array}} \right.}\end{array}\)
5 تعداد ضربان قلب، x دقیقه\(\left( {0 \le x \le 8} \right)\) پس از پایان یک کار سنگین بدنی، طبق رابطهٔ \(y = \frac{{15}}{8}{x^2} - 30x + 200\) به دست می آید. در چه زمان هایی پس از یک کار سنگین بدنی، تعداد ضربان قلب از ١١٠ بیشتر است؟ آیا تمام جواب های به دست آمده قابل قبول اند؟
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}y = \frac{{15}}{8}{x^2} - 30x + 200\\\end{array}\\{y > 110 \Rightarrow x \in ?}\end{array}} \right.\\\\\frac{{15}}{8}{x^2} - 30x + 200 > 110\\\\ \Rightarrow \frac{{15}}{8}{x^2} - 30x + 90 > 0\\\\\frac{{15}}{8}{x^2} - 30x + 90 = 0\\\\ \Rightarrow \Delta = {\left( { - 30} \right)^2} - 4(\frac{{15}}{2})\left( {90} \right) = 900 - 675 = 225 > 0\\\\x = \frac{{ - \left( { - 30} \right) \pm \sqrt {225} }}{{2(\frac{{15}}{8})}} = \frac{{30 \pm 15}}{{\frac{{15}}{4}}} = \\\\\frac{{120 \pm 60}}{{15}} = 8 \pm 4\\\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x = 12\\\end{array}\\{x = 4}\end{array}} \right.\end{array}\)




1736019749.png)















