جواب تمرین صفحه 16 درس 1 هندسه یازدهم (دایره)
تعداد بازدید : 84.75Mپاسخ تمرین صفحه 16 هندسه یازدهم
-گام به گام تمرین صفحه 16 درس دایره
-تمرین صفحه 16 درس 1
-شما در حال مشاهده جواب تمرین صفحه 16 هندسه یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 در شکل های زیر ثابت کنید:
راهنمایی: در قسمت های (ب) و (پ) از نقطۀ B خطی موازی ضلع دیگر زاویه رسم کنید.

الف
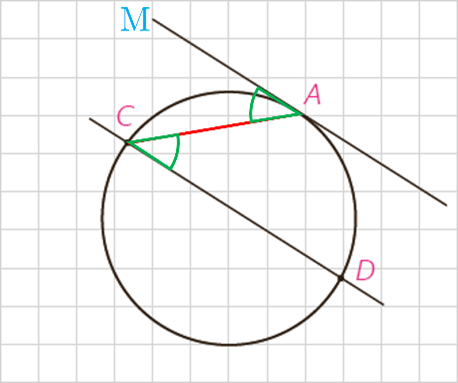
ثابت می شود که کمان های محصور بین یک مماس و وتر موازی در یک دایره با هم برابرند. در شکل مقابل بنا بر قضیه خطوط موازی \(\widehat {MAC} = \widehat {BCA} \) :
\(\widehat {MAC} = \frac{1}{2}\widehat {AC}\) زاویه ظلّی
\(\widehat {ACD} = \frac{1}{2}\widehat {AD}\) زاویه محاطی
\(\widehat {MAC} = \widehat {ACD} \Rightarrow \frac{1}{2}\widehat {AC} = \frac{1}{2}\widehat {AD} \Rightarrow \widehat {AC} = \widehat {AD}\)
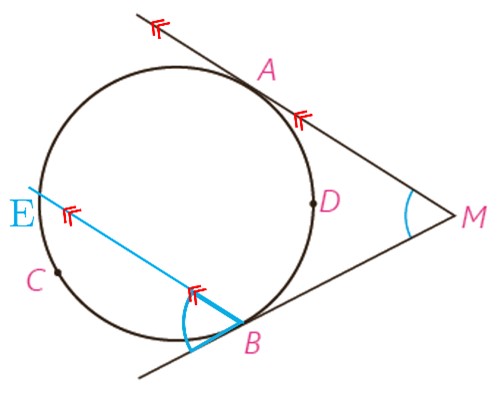
ب
\(\begin{array}{l}\widehat {AMB} = \widehat {EBF} = \frac{{\widehat {EB}}}{2} = \frac{{\widehat {ACB} - \widehat {AF}}}{2}\\\widehat {AE} = \widehat {ADB} \Rightarrow \widehat {AMB} = \widehat {EBF} = \frac{{\widehat {ACB} - \widehat {ADB}}}{2}\end{array}\)
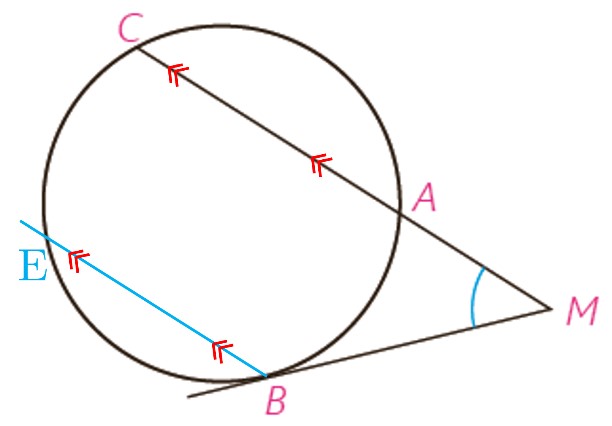
پ
بنا بر قضیه خطوط موازی داریم \(\widehat {CMB} = \widehat {EBF}\):
\(\begin{array}{l}\widehat {CMB} = \widehat {EBF} = \frac{{\widehat {EB}}}{2} = \frac{{\widehat {BC} - \widehat {CE}}}{2}\\\widehat {CE} = \widehat {AB} \Rightarrow \widehat {CMB} = \widehat {EBF} = \frac{{\widehat {BC} - \widehat {AB}}}{2}\end{array}\)
2 در شکل مقابل اندازهٔ زاویهٔ α را به دست آورید.
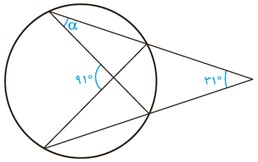
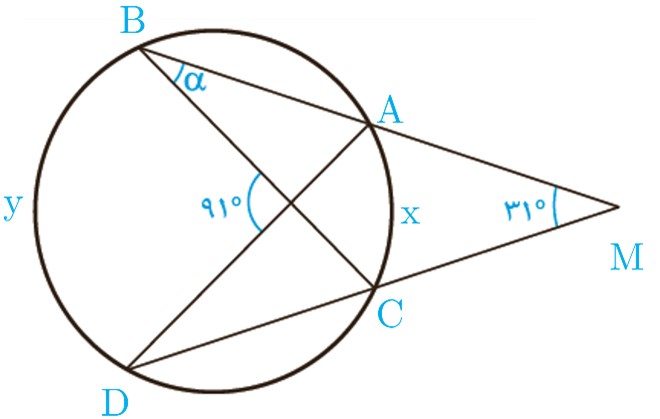
\(\begin{array}{l}\widehat M = \frac{{y - x}}{2} \Rightarrow 2 \times {31^ \circ } = y - x\\\widehat N = \frac{{y + x}}{2} \Rightarrow 2 \times {91^ \circ } = y + x\\ \Rightarrow \left\{ \begin{array}{l}y - x = {62^ \circ }\\y + x = {182^ \circ }\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = {60^ \circ }\\y = {122^ \circ }\end{array} \right.\end{array}\)
3 در شکل اضلاع زاویه های B و C بر دایره مماس اند. اندازهٔ زاویهٔ A چند درجه است؟
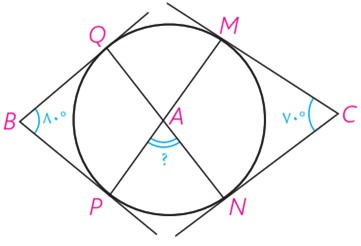
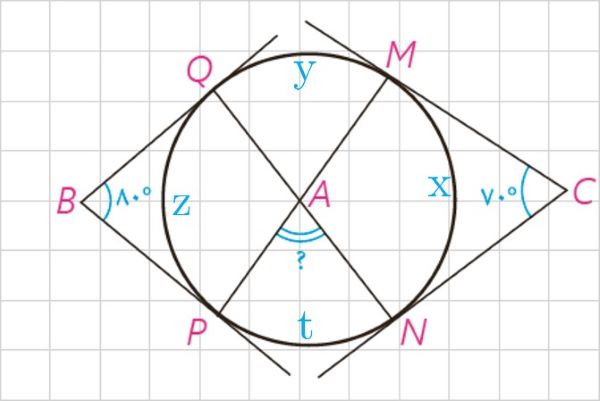
\(\begin{array}{l}{70^ \circ } = \frac{{\left( {y + z + t} \right) - x}}{2} \Rightarrow {140^ \circ } = \left( {y + z + t} \right) - x\\{80^ \circ } = \frac{{\left( {y + x + t} \right) - z}}{2} \Rightarrow {160^ \circ } = \left( {y + x + t} \right) - z\\ \Rightarrow \left\{ \begin{array}{l}{140^ \circ } = \left( {y + z + t} \right) - x\\{160^ \circ } = \left( {y + x + t} \right) - z\end{array} \right.\quad \mathop \Rightarrow \limits^ + \quad \\{300^ \circ } = 2\left( {y + t} \right) \Rightarrow y + t = {150^ \circ }\\\\\widehat A = \frac{{y + t}}{2} \Rightarrow \widehat A = {75^ \circ }\end{array}\)
4 در دایره رسم شده شکل مقابل CD||AB، اندازه کمان CD را به دست آورید.

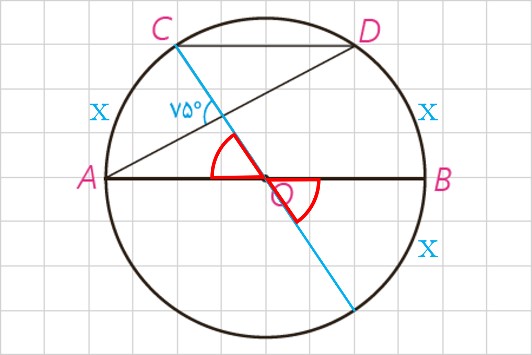
\(\begin{array}{l}{75^ \circ } = \frac{{\left( {x + x} \right) + x}}{2} \Rightarrow x = {50^ \circ }\\\widehat {CD} = {180^ \circ } - 2x \Rightarrow \widehat {CD} = {180^ \circ } - {100^ \circ } = {80^ \circ }\end{array}\)
5 در شکل مقابل، AB قطری از دایره است و وترهای AC و BD موازی اند. ثابت کنید: AC=BD
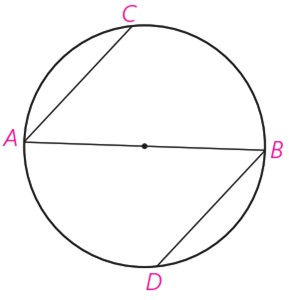
\(\begin{array}{l}AC\parallel DB \Rightarrow \widehat {AD} = \widehat {BC}\\\widehat {ACB} = \widehat {ADB} = {180^ \circ }\\\widehat {ACB} - \widehat {BC} = \widehat {ADB} - \widehat {AD} \Rightarrow \widehat {AC} = \widehat {BD} \Rightarrow AC = BD\end{array}\)
6 دایرۀ C(O,R) مفروض است. از نقطهٔ M در خارج دایره خطی چنان رسم کرده ایم که دایره را در دو نقطهٔ A و B قطع کرده است و MA=R؛ نشان دهید: \(β=3α\)
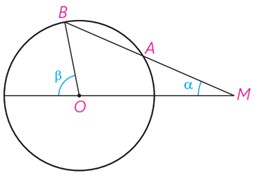
با توجه به فرض مسئله، مثلث های OAM و OAB متساوی الساقین هستند. در مثلث OBM داریم:
\(\beta = 2\alpha + \alpha = 3\alpha\)
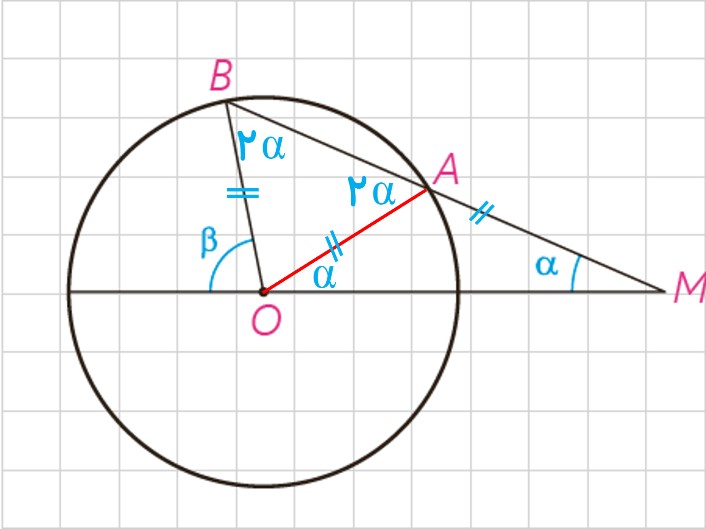
7 در دایرهٔ \(C(O,R)\) ،\(\widehat {AB} = {60^\circ }\) و AB=10 فاصلۀ O از وتر AB را به دست آورید.
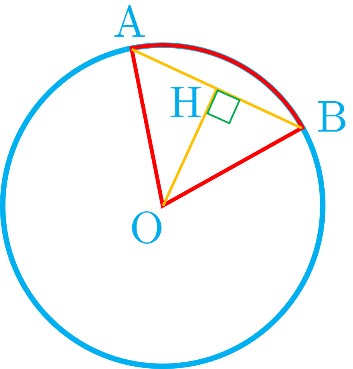
می دانیم که مثلث OAB متساوی الاضلاع است؛ زیرا زاویه مرکزی آن 60 درجه می باشد. در نتیجه زاویه پای ساق های آن نیز 60 درجه می شود. برای پیدا کردن فاصله متر از مرکز باید از نقطه O بر وتر عمود کنیم، سپس طول پاره خط OH را به دست آوریم. قطر عمود بر وتر، وتر را نصف می کند، بنابراین 5 = AH . پس در مثلث قائم الزاویه OAH داریم:
\(\begin{array}{l}OH = \sqrt {O{A^2} - A{H^2}} \\ \Rightarrow OH = \sqrt {{{10}^2} - {5^2}} = \sqrt {75} = 5\sqrt 3 \end{array}\)
8 در دایرهٔ \(C(O,R)\) نشان دهید \(AB>CD \) اگر و تنها اگر \(OH<OH’\) (OH و OH’ قاصلۀ O از دو وتر AB و CD هستند.)
راهنمایی: از O به B و C وصل، و از قضیة فیثاغورس استفاده کنید.
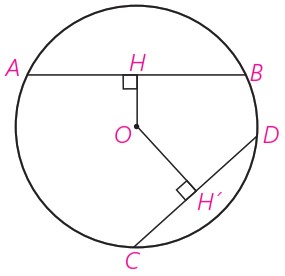
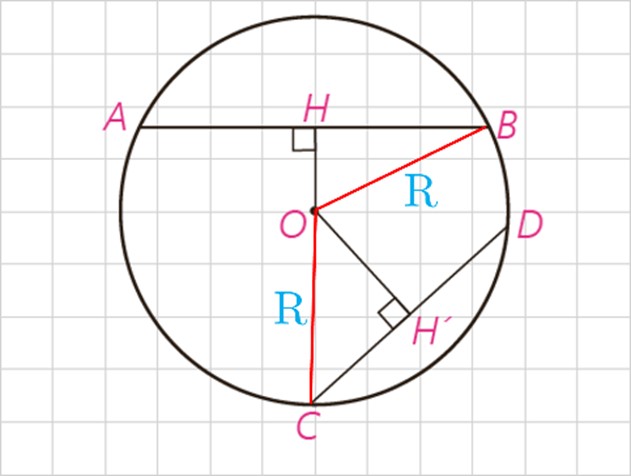
فرض: \(AB > CD \) حکم: \(OH < OH'\)
\(\begin{array}{l}OB = OC = R\quad ,\quad BH = \frac{{AB}}{2}\quad ,\quad CH = \frac{{CD}}{2}\quad \left( 1 \right)\\O\mathop B\limits^\Delta H:\quad H = {90^ \circ } \Rightarrow B{H^2} = {R^2} - O{H^2}\\O\mathop C\limits^\Delta H':\;\;\,H' = {90^ \circ } \Rightarrow C{{H'}^2} = {R^2} - O{{H'}^2}\\AB > CD \Rightarrow \frac{{AB}}{2} > \frac{{CD}}{2}\;\;,\;\;\left( 1 \right) \Rightarrow BH > CH'\\ \Rightarrow B{H^2} > C{{H'}^2}\\ \Rightarrow {R^2} - O{H^2} > {R^2} - O{{H'}^2} \Rightarrow - O{H^2} > - O{{H'}^2}\\ \Rightarrow O{H^2} < O{{H'}^2} \Rightarrow OH < OH'\end{array}\)
فرض: \(OH < OH' \) حکم: \(AB > CD\)
\(\begin{array}{l}OB = OC = R\;\;,\;\;2BH = AB\;\;,\;\;2CH = CD\;\;\left( 1 \right)\\O\mathop B\limits^\Delta H:\;\;H = {90^ \circ } \Rightarrow B{H^2} = {R^2} - O{H^2}\\O\mathop C\limits^\Delta H':\;H' = {90^ \circ } \Rightarrow C{{H'}^2} = {R^2} - O{{H'}^2}\\OH < OH' \Rightarrow O{H^2} < O{{H'}^2}\\ \Rightarrow {R^2} - B{H^2} < {R^2} - C{{H'}^2}\\ \Rightarrow - B{H^2} < - C{{H'}^2} \Rightarrow B{H^2} > C{{H'}^2}\\ \Rightarrow BH > CH'\;\;,\;\;(1)\; \to AB > CD\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















