جواب فعّالیت صفحه 21 درس 1 هندسه یازدهم (دایره)
تعداد بازدید : 84.75Mپاسخ فعّالیت صفحه 21 هندسه یازدهم
-گام به گام فعّالیت صفحه 21 درس دایره
-فعّالیت صفحه 21 درس 1
-شما در حال مشاهده جواب فعّالیت صفحه 21 هندسه یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 فرض کنیم مانند شکل خط m در نقاط T و T’ بر دو دایره مماس است و شعاع های OT و OT’ رسم شده است. فرض کنیم فاصله بین مرکزهای دو دایره برابر d باشد؛ از O’ خطی موازی خط m رسم می کنیم تا شعاع OT را در نقطه ای مانند H قطع کند.
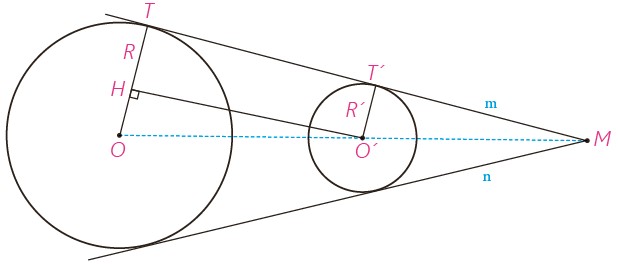
الف TT’O’H مستطیل است؛ چرا؟
ب با توجه به قضیه فیثاغورس در مثلث O’HO، تساوی زیر را توجیه کنید.
\(TT' = \sqrt {{d^2} - {{\left( {R - R'} \right)}^2}} \)
پ با توجه به کار در کلاس قبل بگویید چرا اگر دو مماس مشترک m و n متقاطع باشند، نقطهٔ تقاطع آنها روی خط OO’ خواهد بود؟
ت به مرکز O و به شعاع R-R’ دایره ای رسم کنید. پاره خط O’H برای دایرهٔ رسم شده چگونه خطی است؟
ث فرض کنید دو دایره داده شده، و رسم مماس مشترک خواسته شده باشد. از آنجا که مرکزها و شعاع های دو دایره معلوم است، می توان دایرهٔ مطرح شده در قسمت (ت) را رسم کرد و سپس مماس O’H را بر آن رسم کرد؛ در این صورت چگونه می توانید مماس TT’ را رسم کنید.
الف
شعاع های OT و OT’ بر خط m عمودند و چون خط O’H موازی خط m می باشند، بنابر قضیه خطوط موازی :
\(\widehat {HTT'} = \widehat {HT'T} = \widehat {HO'T'} = \widehat {O'HT} = {90^ \circ }\)
بنابراین چهار ضلعی TT’O’H مستطیل می باشد.
ب
\(\begin{array}{l}\widehat H = {90^ \circ } \Rightarrow O'{H^2} + O{H^2} = O{{O'}^2} \Rightarrow O'{H^2} = O{{O'}^2} - O{H^2}\\\\ \Rightarrow O'H = \sqrt {{d^2} - {{\left( {OT - OT'} \right)}^2}} \\\\\mathop \Rightarrow \limits_{\scriptstyle OT = R\atop\scriptstyle OT' = R'}^{O'H = TT'} \;\;TT' = \sqrt {{d^2} - {{\left( {R - R'} \right)}^2}} \end{array}\)
پ
فرض کنیم این دو مماس مشترک در نقطه M یکدیگر را قطع کنند. با توجه به کار در کلاس قبل، OM و O’M نیم ساز زاویه M هستند و بر هم نیز منطبق اند، در نتیجه نقطه تقاطع مماس ها روی خط OO’ قرار دارد.
ت
پاره خط O’H ، خط مماس بر این دایره می باشد.
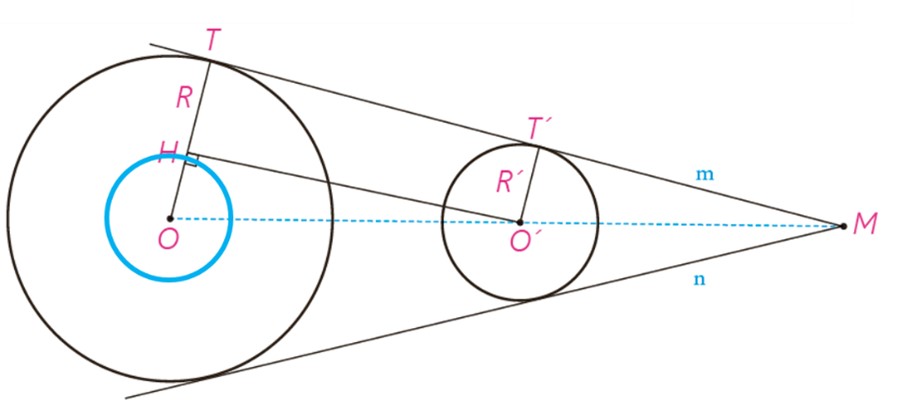
ث
از نقطه O به H وصل می کنیم و امتداد می دهیم تا دایره (C) را در نقطه T قطع کند. سپس از این نقطه خطی موازی O’H رسم می کنیم. این خط در نقطه T’ بر دایره (C’) مماس می شود.
2 دو مماس مشترک داخلی l و k بر دو دایره متخارج مطابق شکل رسم شده است. با به کار بردن قضیه فیثاغورس در مثلث O’OH نشان دهید:
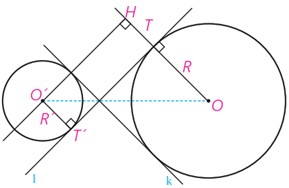
\(TT' = \sqrt {{d^2} - {{\left( {R - R'} \right)}^2}} \)
با توجه به شکل چهار ضلعی THO’T’ مستطیل است. پس TT’=OH . همچنین TH=O’T’=R’ . و در نتیجه : OH= R+R’ .
\(\begin{array}{l}O'\mathop O\limits^\Delta H:\quad \widehat H = {90^ \circ } \Rightarrow O'{H^2} = O{{O'}^2} - O{H^2}\\\\\mathop \Rightarrow \limits_{\scriptstyle OH = R + R'\atop\scriptstyle OO' = d}^{TT' = O'H} \;\;\;TT' = \sqrt {{d^2} - {{\left( {R + R'} \right)}^2}} \end{array}\)
3 دو دایره مماس. دو دایره را که فقط یک نقطه مشترک داشته باشند، مماس می نامند. در این نقطه مشترک یک خط بر هر دو مماس است. اگر مرکزهای دو دایره در دوطرف این مماس باشند، آن دو دایره، مماس برونی است و اگر هر دو مرکز در یک طرف این مماس باشند، آنها را مماس درونی می نامند.
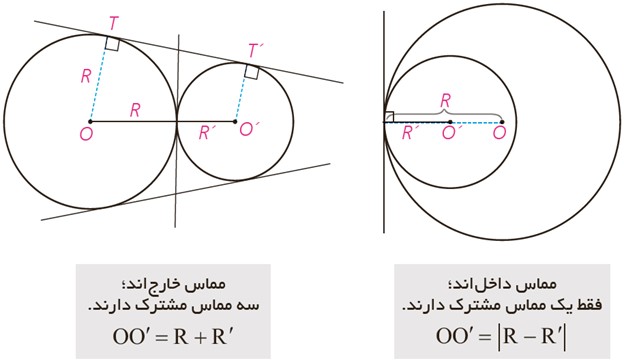
با استفاده از دستور محاسبهٔ طول مماس مشترک خارجی، نشان دهید در دو دایره مماس خارج، \(TT' = 2\sqrt {RR'} \)
\(\begin{array}{l}TT' = \sqrt {{d^2} - {{\left( {R - R'} \right)}^2}} \\\\\mathop \Rightarrow \limits^{d = R + R'} \;\;TT' = \sqrt {{{\left( {R + R'} \right)}^2} - {{\left( {R - R'} \right)}^2}} = \sqrt {4RR'} = 2\sqrt {RR'} \\\\ \Rightarrow TT' = \sqrt {{R^2} + {{R'}^2} + 2RR' - \left( {{R^2} + {{R'}^2} - 2RR'} \right)} \end{array}\)
4 دو دایره متقاطع. دو دایره را که دو نقطه مشترک داشته باشند، متقاطع می نامند. در این حالت دو دایره، فقط دو مماس مشترک دارند.
و \(|R – R’| < OO’ < R + R’ \)؛ چرا؟
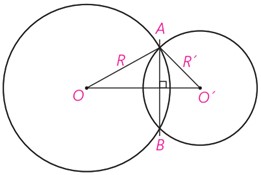
پاره خط AB، که دوسر آن روی هر دو دایره است، وتر مشترک دو دایره متقاطع است. چرا پاره خط OO’ عمودمنصف وتر مشترک AB است؟
با توجه به نامساوی مثلث در مثلث AOO’ داریم:
\(OO' < R + R'\quad \left( 1 \right)\)
\(\begin{array}{l}\left. \begin{array}{l}R' < OO' + R \Rightarrow - OO' < R - R'\\R < OO' + R' \Rightarrow R - R' < OO'\end{array} \right\}\\\\ \Rightarrow - OO' < R - R' < OO'\\\\ \Rightarrow \left| {R - R'} \right| < OO'\quad \left( 2 \right)\\\\\mathop \Rightarrow \limits^{\left( 1 \right),\left( 2 \right)} \;\;\left| {R - R'} \right| < OO' < R + R'\end{array}\)
\(OA=OB=R\) و \(O’A=O’B=R’ \). بنابر خاصیت عمودمنصف نقاط O و O’ روی عمود منصف AB قرار دارد و چون عمود منصف هر پاره خط یکتا است، در نتیجه پاره خط OO’ عمود منصف وتر مشترک AB است.
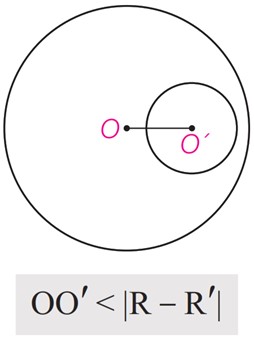
5 دو دایره متداخل. دو دایره را که تمام نقاط یکی درون دیگری باشد، متداخل می نامیم. دو دایره متداخل هیچ مماس مشترک ندارند و در آنها \(OO’ < |R – R’|\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















