جواب تمرین صفحه 23 درس 1 هندسه یازدهم (دایره)

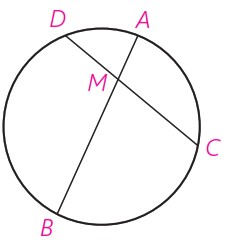
\(\begin{array}{*{20}{l}}{\frac{{DM}}{{MC}} = \frac{1}{2} \Rightarrow \frac{{DM}}{{DC}} = \frac{1}{3} \Rightarrow \frac{{DM}}{9} = \frac{1}{3}}\\{ \Rightarrow DM = 3 \Rightarrow MC = 6}\\{DM \cdot MC = AM \cdot BM\;\;,\;\;AM = x}\\{ \Rightarrow 3 \times 6 = x\left( {11 - x} \right) \Rightarrow {x^2} - 11x + 18 = 0}\\{ \Rightarrow \left( {x - 9} \right)\left( {x - 2} \right) = 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{x = 9 \otimes }\end{array}} \right. \Rightarrow x = 2}\\{ \Rightarrow \frac{{AM}}{{MB}} = \frac{2}{9}}\end{array}\)

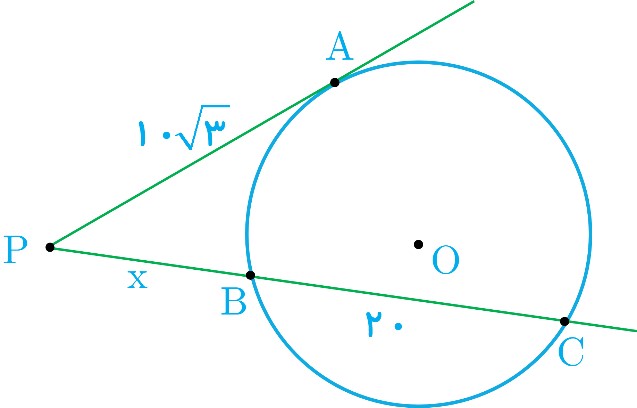
\(\begin{array}{l}P{A^2} = PB \cdot PC \Rightarrow {\left( {10\sqrt 3 } \right)^2}\\ = x\left( {x + 20} \right) \Rightarrow {x^2} + 20x - 300 = 0\\ \Rightarrow \left( {x - 10} \right)\left( {x + 30} \right) = 0\\ \Rightarrow \left\{ \begin{array}{l}x = 10\\x = - 30\;\; \otimes \end{array} \right. \Rightarrow x = 10\\\\ \Rightarrow \left\{ \begin{array}{l}PB = 10\\PC = 30\end{array} \right.\end{array}\)

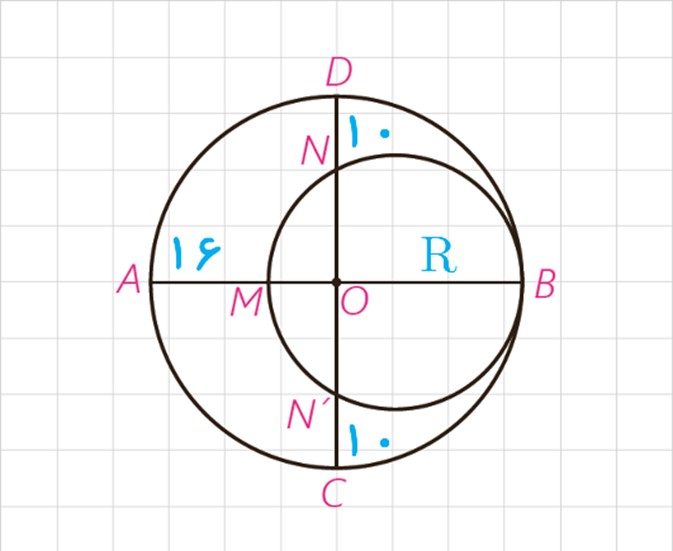
\(\begin{array}{l}OB \cdot OM = ON \cdot ON'\\ \Rightarrow R\left( {R - 16} \right) = \left( {R - 10} \right)\left( {R - 10} \right)\\ \Rightarrow {R^2} - 16R = {R^2} - 20R + 100\\ \Rightarrow 4R = 100 \Rightarrow R = 25\\R' = \frac{{BM}}{2} = \frac{{2R - 16}}{2} = \frac{{50 - 16}}{2}\\ \Rightarrow R' = 17\end{array}\)

با توجه به مبحث « رسم مماس بر دایره از نقطه ای خارج دایره » در ص 19 می دانیم که از هر نقطه خارج دایره طول مماس های رسم شده با هم برابرند. بنابراین داریم:

\(\left. \begin{array}{l}MT = M{T_1}\\MT = M{T_2}\\MT = M{T_3}\\MT = M{T_4}\end{array} \right\} \Rightarrow M{T_1} = M{T_2} = M{T_3} = M{T_4} = \cdots\)

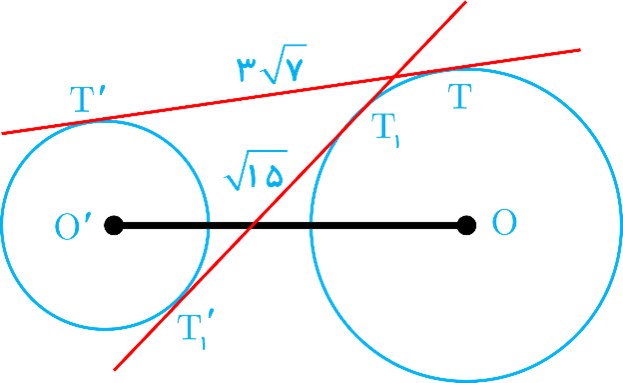
\(\begin{array}{l}\left\{ \begin{array}{l}T{{T'}^2} = {d^2} - {\left( {R - R'} \right)^2}\\{T_1}{{T'}_1}^{\;2} = {d^2} - {\left( {R + R'} \right)^2}\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}63 = 64 - {\left( {R - R'} \right)^2}\\15 = 64 - {\left( {R + R'} \right)^2}\end{array} \right.\\\\\left\{ \begin{array}{l}R - R' = 1\\R + R' = 7\end{array} \right. \Rightarrow \left\{ \begin{array}{l}R = 4\\R' = 3\end{array} \right.\end{array}\)

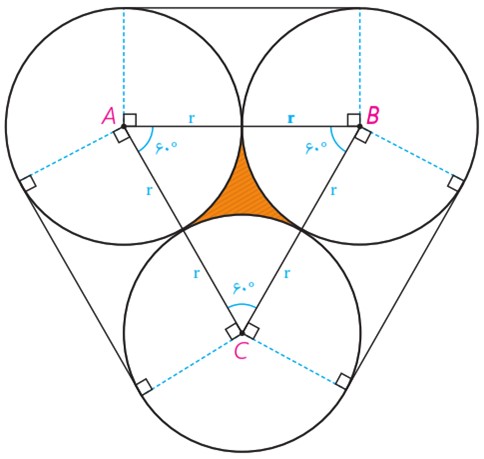
مجموع سه قطاع با زاویه 120 درجه تشکیل یک دایره کامل می دهد؛ بنابراین داریم:

طول نخ \( 2r + 2r + 2r =\) محیط دایره \(6r + 2πr=\)

مجموع سه قطاع با زاویه 60 درجه تشکیل یک نیم دایره می دهد؛ بنابراین داریم:

= مساحت ناحیه هاشور خورده ABC مساحت مثلث – مساحت نیم دایره

\(= \frac{{\sqrt 3 }}{4}{\left( {2r} \right)^2} - \frac{{\pi {r^2}}}{2} = \sqrt 3 {r^2} - \frac{{\pi {r^2}}}{2} = {r^2}\left( {\sqrt 3 - \frac{\pi }{2}} \right)\)

 با توجه به شکل OA=R و O’A=R’ . در نتیجه :

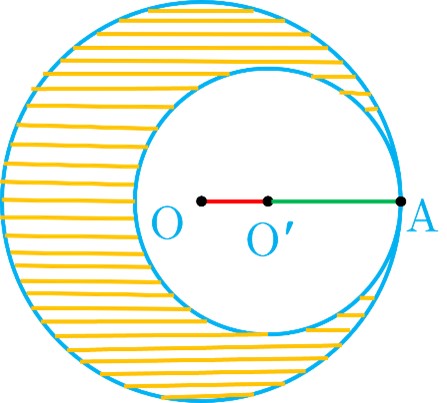
مساحت ناحیه هاشور زده \(= \pi {R^2} - \pi {{R'}^2} = 16\pi\)

\(\begin{array}{l} = \pi {R^2} - \pi {{R'}^2} = 16\pi \\ \Rightarrow {R^2} - {{R'}^2} = 16\\ \Rightarrow \left( {R - R'} \right)\left( {R + R'} \right) = 16\;\;,\;\;OO' = R - R' = 2\\ \Rightarrow 2\left( {R + R'} \right) = 16 \Rightarrow R + R' = 8\\\left\{ \begin{array}{l}R - R' = 2\\R + R' = 8\end{array} \right. \Rightarrow \left\{ \begin{array}{l}R = 5\\R' = 3\end{array} \right.\end{array}\)

مثلث OAB مثلث متساوی الساقین است و زاویه مرکزی \(\widehat O = {60^ \circ } \) است. پس این مثلث متساوی الاضلاع است.

A = مساحت قسمت رنگی – مساحت قطاع 60 درجه OAB مساحت مثلث

\(\begin{array}{l}A = \frac{{\pi {r^2}}}{{360}}\alpha - \frac{{\sqrt 3 }}{4} \times {r^2}\\ = \frac{{16\pi }}{{360}} \times 60 - 4\sqrt 3 \\ \Rightarrow A = \frac{8}{3}\pi - 4\sqrt 3 \end{array}\)