درسنامه کامل هندسه یازدهم
تعداد بازدید : 515.09kخلاصه نکات هندسه یازدهم - درسنامه شب امتحان هندسه یازدهم - جزوه شب امتحان هندسه یازدهم نوبت اول
دایره
فصل 1 : دایره
دایره
دایره پر کاربرد ترین شکل در طبیعت، معماری، صنعت و .... می باشد. به عنوان یک مسئله ریاضی می توان ثابت کرد، در بین تمام شکل های هندسی با محیط ثابت دایره دارای بیشترین مساحت است.
تعریف دایره
مجموعه نقاطی از صفحه که از نقطه ای ثابت O به فاصله ثابت r باشند.
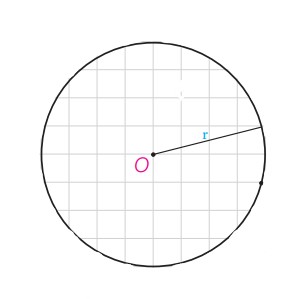
معمولا دایره C به مرکز O و شعاع r را با نماد \(C\left( {O,r} \right)\) نمایش می دهیم.
شعاع دایره
پاره خطی که یک سر آن مرکز دایره و سر دیگر آن نقطه ای روی دایره باشد.

وتر دایره
پاره خطی که دو سر آن روی دایره باشد.
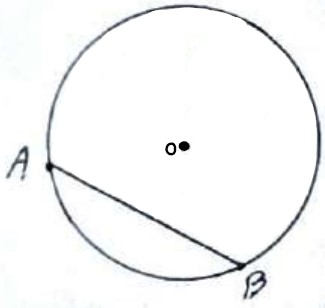
قطر دایره
بزرگترین وتر دایره که از مرکز دایره می گذرد.
تهیه کننده: امیرحسین مطلبی
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
وضعیت نقطه و دایره
فصل 1 : دایره
وضعیت نقطه و دایره
هر نقطه نسبت به دایره سه وضعیت داخل، روی و بیرون دایره را دارد. تشخیص این موضوع به فاصله نقطه از مرکز دایره وابسته است.
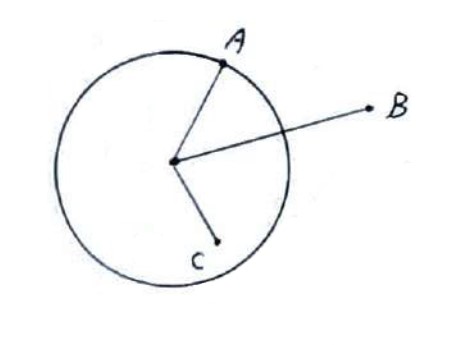
\(\begin{array}{l}OA = r\\\\OB > r\\\\OC < r\end{array}\)
وضعیت نسبی خط و دایره
یک خط با یک دایره سه وضعیت متخارج، مماس و متقاطع را دارد، که از روی فاصله مرکز دایره تا خط قابل تشخیص است.
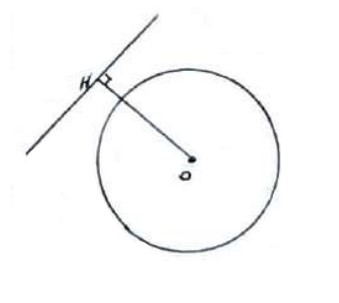
متخارج
\(OH > r\)
خط و دایره نقطه مشترک ندارند.
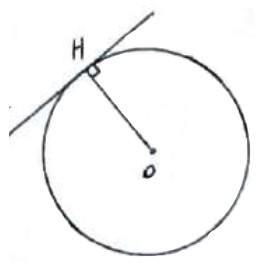
مماس
\(OH = r\)
خط و دایره یک نقطه اشتراک دارند.
متقاطع
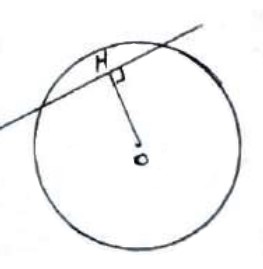
\(OH < r\)
خط و دایره دو نقطه اشتراک دارند.
یک خط بر دایره مماس است، اگر و تنها اگر خط در نقطه تماس بر شعاع دایره عمود باشد.
تهیه کننده: امیرحسین مطلبی
زوایای مرکزی و محاطی
فصل 1 : دایره
کمان
کمان دایره شامل دو نقطه روی دایره و تمام نقاط بین آن دو نقطه است. (هر کمان قسمتی از محیط دایره است.)
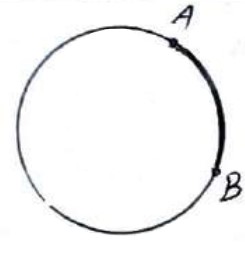
در شکل بالا دو نقطه A و B روی محیط دایره و کمان \(AB\) مشخص شده است.
زاویه مرکزی
زاویه ای که راس آن روی مرکز دایره و ضلع های آن شعاع دایره باشند.
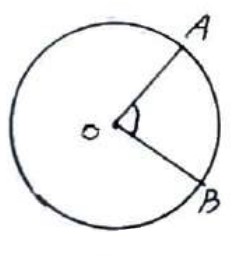
اندازه زاویه مرکزی برابر اندازه کمان مقابلش است:
\(\hat O = \mathop {AB}\limits^\frown \,\)
زاویه محاطی
زاویه ای است که راسش روی محیط دایره و ضلع هایش وتر های دایره باشند.
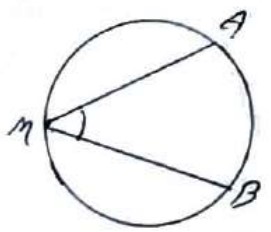
اندازه زاویه محاطی نصف کمان مقابلش است:
\(\hat M = \frac{{\mathop {AB}\limits^\frown }}{2}\)
اندازه کمان
همان اندازه زاویه مرکزی مقابل به آن کمان می باشد و واحد آن درجه است. در دایره های هم مرکز کمان هایی با طول متفاوت؛ دارای اندازه برابر می باشند.
1 رابطه ی بین طول کمان AB و اندازه کمان AB به صورت زیر است:
\(\frac{{\left| {AB} \right|}}{{360}} = \frac{{\mathop {AB}\limits^\frown }}{{2\pi r}}\)
(\(\left| {AB} \right|\) اندازه AB است.)
2 دایره یک کمان است که طول آن \(2\pi r\) و اندازه آن \({360^0}\) می باشد.
در شکل زیر طول و اندازه کمان های AB و CD را بدست آورید.
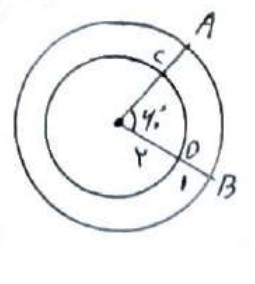
اندازه AB = \({60^0}\)
\(\begin{array}{*{20}{l}}\begin{array}{l}\frac{{\left| {AB} \right|}}{{360}} = \frac{{\mathop {AB}\limits^\frown }}{{2\pi r}} \Rightarrow \frac{{60}}{{360}} = \frac{{\mathop {AB}\limits^\frown }}{{2\pi 3}}\\\end{array}\\{ \Rightarrow \mathop {AB}\limits^\frown = \frac{1}{6} \times 6\pi = \pi }\end{array}\)
اندازه CD = \({60^0}\)
\(\begin{array}{*{20}{l}}\begin{array}{l}\frac{{\left| {CD} \right|}}{{360}} = \frac{{\mathop {CD}\limits^\frown }}{{2\pi r}} \Rightarrow \frac{{60}}{{360}} = \frac{{\mathop {CD}\limits^\frown }}{{2\pi 2}}\\\end{array}\\{ \Rightarrow \mathop {CD}\limits^\frown = \frac{1}{6} \times 4\pi = \frac{{2\pi }}{3}}\end{array}\)
تهیه کننده: امیرحسین مطلبی
قطاع
فصل 1 : دایره
قطاع
ناحیه ای از درون و روی دایره را، که به دو شعاع دایره و آن دایره محدود است یک قطاع دایره می نامند.
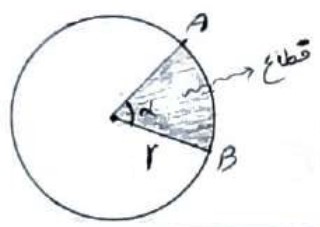
طول کمان نظیر قطاع
اگر طول کمان AB نظیر قطاع را L در نظر بگیریم از رابطه زیر حاصل می شود:
\(L = \frac{{2\pi r}}{{360}}\alpha \)
اثبات
\(\begin{array}{l}\frac{{\left| {AB} \right|}}{{360}} = \frac{{\mathop {AB}\limits^\frown {\mkern 1mu} }}{{2\pi r}} \Rightarrow \frac{\alpha }{{360}} = \frac{L}{{2\pi r}}\\\\ \Rightarrow L = \frac{{2\pi r}}{{360}}\alpha \end{array}\)
مساحت قطاع
اگر مساحت قطاع که زاویه مرکزی آن \(\alpha \) می باشد را S در نظر بگیریم:
\(S = \frac{{\pi {r^2}}}{{360}}\alpha \)
اثبات:
می دانیم یک درجه، \(\frac{1}{{360}}\) دایره است، پس مساحت قطاعی که زاویه مرکزی آن 1 درجه است؛ \(\frac{1}{{360}}\) مساحت دایره است؛ در نتیجه مساحت قطاعی که زاویه مرکزی آن \(\alpha \) درجه است، \(\frac{\alpha }{{360}}\) مساحت دایره است.
مساحت قطاع = \(\frac{\alpha }{{360}} \Rightarrow S = \frac{\alpha }{{360}} = \pi {r^2} \Rightarrow S = \frac{{\pi {r^2}}}{{360}}\alpha \)
1 طول کمان های AB و CD و مساحت قسمت هاشور خورده را بدست آورید.
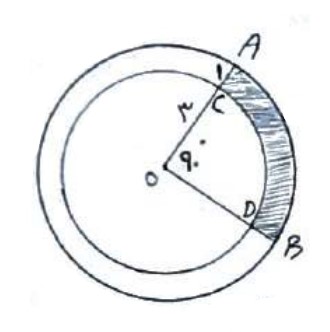
طول کمان AB = \(\frac{{2\pi r}}{{360}}\alpha = \frac{{2\pi 4}}{{360}} \times 90 = 2\pi \)
طول کمان CD = \(\frac{{2\pi r}}{{360}}\alpha = \frac{{2\pi \times 3}}{{360}} \times 90 = \frac{{3\pi }}{2}\)
مساحت قسمت هاشور خورده: \({S_{A\mathop O\limits^\Delta B}} - {S_{C\mathop O\limits^\Delta D}} = \)
\(\begin{array}{l}\frac{{\pi \times {4^2}}}{{360}} \times 90 - \frac{{\pi \times {3^2}}}{{360}} \times 90 = \\\\\frac{{16\pi }}{4} - \frac{{9\pi }}{4} = \frac{{7\pi }}{4}\end{array}\)
2 در شکل زیر اگر O مرکز دایره و مساحت ناحیه هاشور خورده برابر 18 باشد، طول کمان AB را بدست آورید. (\(\pi = 3\))
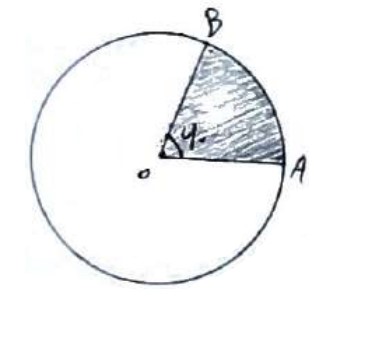
\(\begin{array}{l}{S_{A\mathop O\limits^\Delta B}} = 18 \Rightarrow \frac{{\pi {r^2}}}{{360}} \times 60 = 18\\\\ \Rightarrow \frac{{3{r^2}}}{6} = 18 \Rightarrow {r^2} = 36 \Rightarrow r = 6\end{array}\)
طول کمان AB = \(\frac{{2\pi r}}{{360}}\alpha = \frac{{2\pi 6}}{{360}} \times 60 = \)
\(2\pi = 2 \times 3 = 6\)
تهیه کننده: امیرحسین مطلبی
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
وتر و کمان نظیر آن
فصل 1 : دایره
وتر و کمان نظیر آن
در شکل زیر کمان AB نظیر و وتر AB می باشد.
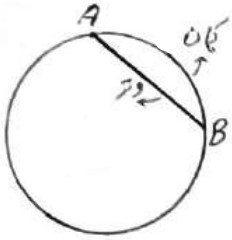
مثال
ثابت کنید در هر دایره کمان های نظیر دو وتر مساوی باهم برابرند و برعکس.
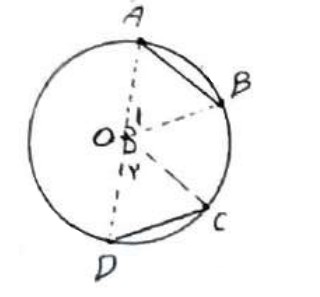
فرض: \(AB = CD\) برابری دو وتر
حکم: \(\mathop {{\rm{AB}}}\limits^\frown {\mkern 1mu} = \mathop {{\rm{CD}}}\limits^\frown {\mkern 1mu} \) برابری دو کمان
\(\begin{array}{*{20}{l}}{AB = CD}\\{}\\{OA = OD}\\{}\\{OB = OC}\\{}\\\begin{array}{l} \Rightarrow O\mathop {{\rm{ }}A}\limits^\Delta B \cong O\mathop {{\rm{ }}D}\limits^\Delta C \Rightarrow {{\hat O}_1} = {{\hat O}_2}\\\\ \Rightarrow \mathop {{\rm{AB}}}\limits^\frown {\mkern 1mu} = \mathop {{\rm{CD}}}\limits^\frown \end{array}\end{array}\)
حال عکس این فرض را اثبات می کنیم:
فرض: \(\mathop {{\rm{AB}}}\limits^\frown {\mkern 1mu} = \mathop {{\rm{CD}}}\limits^\frown \) برابری دو کمان
حکم: \(AB = CD\) برابری دو وتر
\(\begin{array}{*{20}{l}}{\mathop {{\rm{AB}}}\limits^\frown {\mkern 1mu} = \mathop {{\rm{CD}}}\limits^\frown \Rightarrow {{\hat O}_1} = {{\hat O}_2}}\\{}\\{OA = OD}\\{}\\{OB = OC}\\{}\\{ \Rightarrow O\mathop {{\rm{ }}A}\limits^\Delta B \cong O\mathop {{\rm{ }}C}\limits^\Delta D \Rightarrow AB = CD}\end{array}\)
قضیه 1
در هر دایره، قطر عمود بر وتر، آن وتر و کمان نظیر آن وتر را نصف می کند.
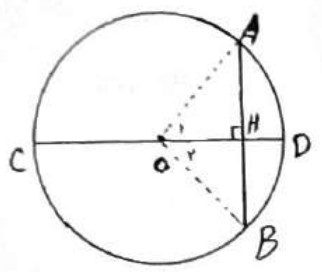
فرض: \(CD \bot AB\)
حکم: \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}AH = BH\\\end{array}\\{\mathop {{\rm{AD}}}\limits^\frown {\mkern 1mu} = \mathop {{\rm{BD}}}\limits^\frown }\end{array}} \right.\)
\(\begin{array}{*{20}{l}}{OA = OB}\\{}\\{OH = OH}\\{}\\\begin{array}{l} \Rightarrow O\mathop {{\rm{ }}A}\limits^\Delta H \cong O\mathop {{\rm{ }}B}\limits^\Delta H \Rightarrow {{\hat O}_1} = {{\hat O}_2}\\\\ \Rightarrow \mathop {{\rm{AD}}}\limits^\frown {\mkern 1mu} = \mathop {{\rm{BD}}}\limits^\frown \end{array}\end{array}\)
عکس قضیه 1
اگر قطری از دایره، وتر و کمان نظیر آن وتر را نصف کند، آنگاه قطر بر وتر عمود است.
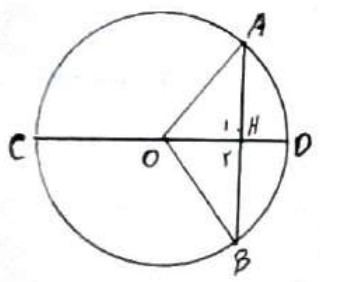
فرض: \({\rm{AH = BH}}\,\,\,{\rm{,}}\,\,\,\mathop {{\rm{AD}}}\limits^\frown {\mkern 1mu} = \mathop {{\rm{BD}}}\limits^\frown \)
حکم: \(CD \bot AB\)
\(\begin{array}{l}AH = BH\\\\OH = OH\\\\OA = OB\\\\ \Rightarrow O\mathop A\limits^\Delta H \cong O\mathop B\limits^\Delta H \Rightarrow {H_1} = {H_2}\\\\ \Rightarrow {{\hat H}_1} = {{\hat H}_2} \Rightarrow CD \bot AB\end{array}\)
قضیه 2
اندازه هر زاویه محاطی برابر است با نصف اندازه کمان مقابل به آن زاویه.
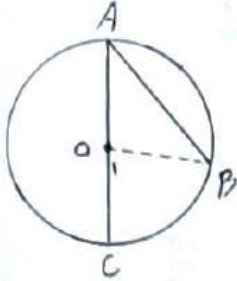
فرض: زاویه محاطی \(\hat A\)
حکم: \(\hat A = \frac{{\mathop {BC}\limits^\frown {\mkern 1mu} }}{2}\)
اثبات:
با وصل کردن B به O داریم:
\(\begin{array}{*{20}{l}}{{{\hat O}_1} = \hat A + \hat B}\\{}\\{O\mathop {{\rm{ }}A}\limits^\Delta B:\hat A = \hat B}\\{}\\{ \Rightarrow {{\hat O}_1} = 2\hat A \Rightarrow \hat A = \frac{{{{\hat O}_1}}}{2} \Rightarrow {{\hat O}_1} = \mathop {BC}\limits^\frown {\mkern 1mu} }\\{}\\{ \Rightarrow \hat A = \frac{{\mathop {BC}\limits^\frown {\mkern 1mu} }}{2}}\end{array}\)
1 در قضیه بالا یکی از اضلاع زاویه محاطی قطر دایره بود. اما می توان حالت های دیگری را برای قضیه بالا در نظر گرفت، مثلا دو ضلع زاویه محاطی دو طرف مرکز دایره باشند، یا دو ضلع زاویه محاطی در یک طرف مرکز باشند.
2 زاویه محاطی زیر به قطر دایره، \({90^0}\) (قائمه) است.
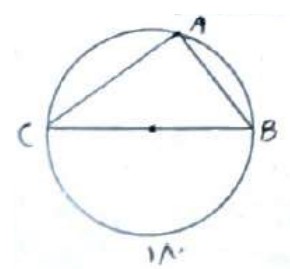
محاطی مقابل قطر \(\hat A = \frac{{\mathop {BC}\limits^\frown {\mkern 1mu} }}{2} = \frac{{{{180}^ \circ }}}{2} = {90^ \circ }\)
1 دایره \(C\left( {O,36} \right)\) و وتر AB به فاصله 10 از مرکز دایره مفروضند. طول وتر AB را بدست آورید.
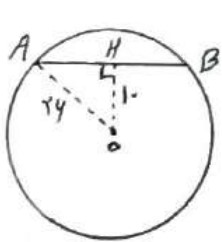
رابطه فیثاغورث: \(O{A^2} = A{H^2} + O{H^2}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {{26}^2} = A{H^2} + {{10}^2}}\\{}\\\begin{array}{l} \Rightarrow A{H^2} = {26^2} - {10^2}\\\\ \Rightarrow A{H^2} = 576\end{array}\\{}\\{ \Rightarrow AH = 24}\end{array}\)
می دانیم قطر عمود بر وتر، وتر را نصف می کند پس، \(AH = BH = 24\) و در نتیجه:
\(AB = 2 \times 24 = 48\)
2 در شکل زیر اندازه زاویه های X و Y را بدست آورید.
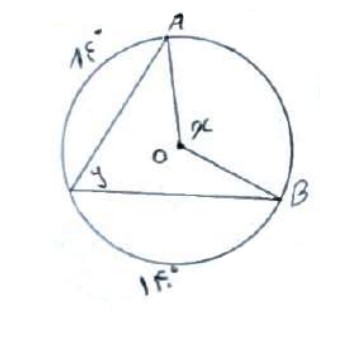
\(AB + {140^0} + {84^0} = {360^0} \Rightarrow AB = {136^0}\)
زاویه مرکزی \(\hat X = AB = {136^0}\)
زاویه محاطی \(\hat Y = \frac{{AB}}{2} = \frac{{136}}{2} = {68^0}\)
تهیه کننده: امیرحسین مطلبی
زاویه ظلی
فصل 1 : دایره
زاویه ظلی
زاویه ای است که راس آن روی دایره قرار دارد و یک ضلع آن مماس بر دایره و ضلع دیگر آن (قاطع دایره) وتر دایره می باشد.
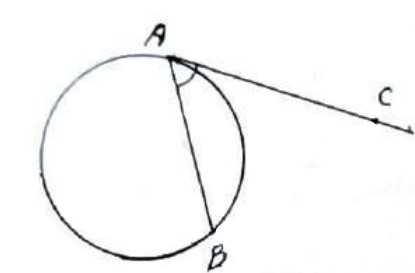
در شکل بالا زاویه \(B\hat AC\) ظلی است.
قضیه
اندازه هر زاویه ظلی برابر نصف کمان رو به روی آن است.
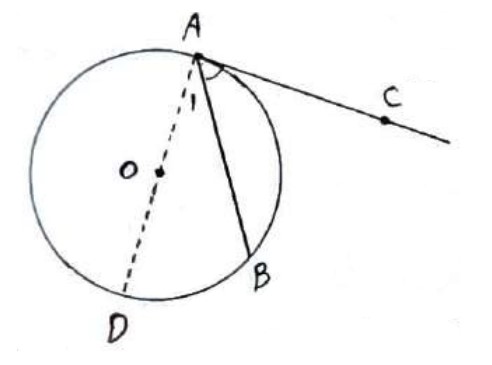
فرض: ظلی \(\hat A\)
حکم: \(\hat A = \frac{{AB}}{2}\hat A = \frac{{\mathop {AB}\limits^\frown {\mkern 1mu} }}{2}\)
قطر گذرنده از A را رسم می کنیم تا دایره را در D قطع کند.
\(\begin{array}{*{20}{l}}{D\hat AC = {{90}^0} \Rightarrow D\hat AC = \frac{{\mathop {AD}\limits^\frown {\mkern 1mu} }}{2}}\\{}\\{{{\hat A}_1} = \frac{{\mathop {BD}\limits^\frown {\mkern 1mu} }}{2}}\\{}\\\begin{array}{l} \Rightarrow D\hat AC - {{\hat A}_1} = \frac{{\mathop {AD}\limits^\frown {\mkern 1mu} - \mathop {BD}\limits^\frown {\mkern 1mu} }}{2}\\\\ \Rightarrow \hat A = \frac{{\mathop {AB}\limits^\frown {\mkern 1mu} }}{2}\end{array}\end{array}\)
1 با توجه به شکل مقابل اندازه زاویه ظلی \(\alpha \) را بدست آورید.
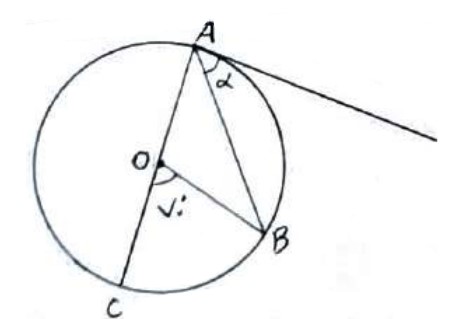
مرکزی: \(C\hat OB = {70^0} \Rightarrow BC = {70^0}\)
قطر است \({AC \Rightarrow \mathop {AB}\limits^\frown = {{180}^ \circ } - {{70}^ \circ } = {{110}^ \circ }}\)
\({\alpha = \frac{{AB}}{2} = \frac{{{{110}^ \circ }}}{2} = {{55}^ \circ }}\)
2 در شکل زیر AT بر دایره در نقطه A مماس است، با توجه به شکل زیر مقدار X و Y را بدست آورید.
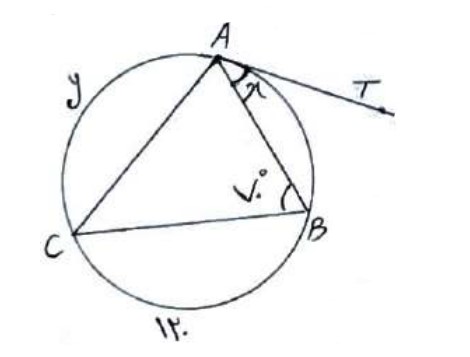
محاطی \(\hat B = \frac{{\mathop {AC}\limits^\frown {\mkern 1mu} }}{2} \Rightarrow \mathop {AC}\limits^\frown = 2 \times {70^ \circ } \Rightarrow \hat Y = {140^ \circ }\)
\(\begin{array}{*{20}{l}}{\mathop {AB}\limits^\frown = {{360}^ \circ } - \left( {{{120}^ \circ } + {{140}^ \circ }} \right) = {{100}^ \circ }}\\{}\\{\hat X = \frac{{\mathop {AB}\limits^\frown {\mkern 1mu} }}{2} = \frac{{{{100}^ \circ }}}{2} = {{50}^ \circ }}\end{array}\)
تهیه کننده: امیرحسین مطلبی
زاویه بین وتر های متقاطع
فصل 1 : دایره
زاویه بین وتر های متقاطع
الف)
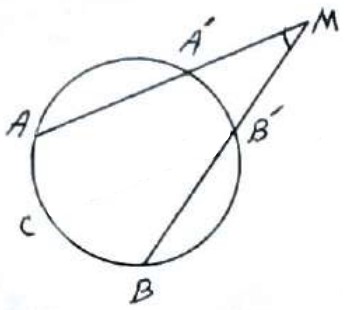
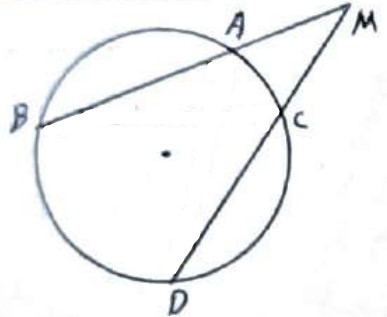
اگر دو وتر در خارج دایره متقاطع باشند، زاویه بین آنها برابر است با نصف تفاضل دو کمان مقابل به آن زاویه:
\(\hat M = \frac{{AB - A'B'}}{2}\)
اثبات (روش اول)
از \(B'\) خطی موازی \(AA'\) رسم می کنیم تا دایره را در C قطع کند.
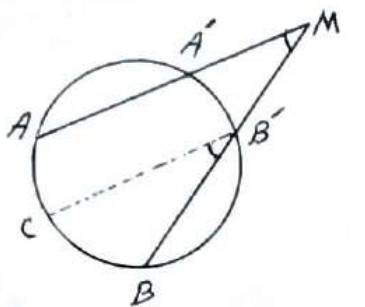
\(\begin{array}{l}AA'\parallel CB' \Rightarrow \hat M = \hat B' = \frac{{BC}}{2}\\\\ \Rightarrow \frac{{AB - AC}}{2} = \frac{{AB - A'B'}}{2}\end{array}\)
اثبات (روش دوم)
از \(B'\) به A وصل می کنیم، زاویه \(B'\) زاویه خارجی مثلث \(A\mathop M\limits^\Delta B\) است.
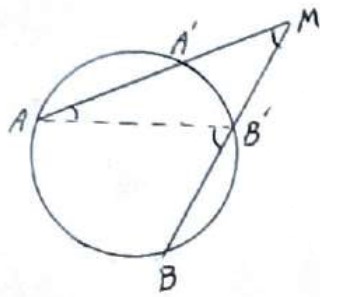
\(\begin{array}{l}\hat B' = \hat A = \hat M \Rightarrow \hat M = \hat B' - \hat A\\\\ \Rightarrow \frac{{AB}}{2} - \frac{{A'B'}}{2} \Rightarrow \frac{{AB - A'B'}}{2}\end{array}\)
ب) اگر دو وتر در داخل دایره متقاطع باشند، زاویه بین آنها برابر است با نصف مجموع دو کمان مقابل به آن زاویه.
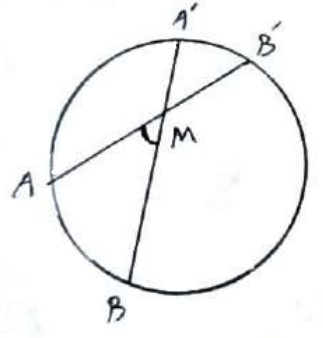
\(\hat M = \frac{{AB + A'B'}}{2}\)
اثبات
از A به \(\hat A\) وصل کنیم، زاویه مشخص شده M زاویه خارجی برای مثلث \(A\mathop {A'}\limits^\Delta M\) می باشد.
خارجی \(\begin{array}{l}\hat M = \hat A + \hat A' = \frac{{A'B'}}{2} + \frac{{AB}}{2}\\\\ \Rightarrow \hat M = \frac{{AB + A'B'}}{2}\end{array}\)
1 با توجه به شکل زیر مقدار های X و Y را تعیین کنید.
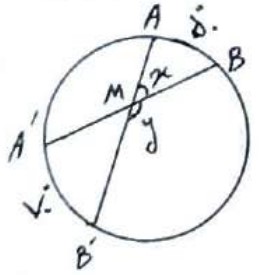
\(\begin{array}{l}\hat X = \frac{{50 + 70}}{2} = \frac{{120}}{2} = {60^0}\\\\\hat Y = 180 - X = 180 - 60 = {120^0}\end{array}\)
2 اندازه زاویه \(\alpha \) را در شکل زیر بیابید.
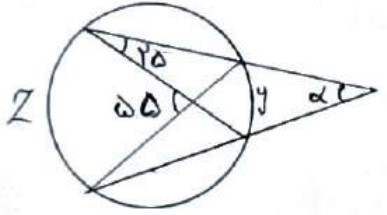
\(\begin{array}{l}25 = \frac{Y}{2} \Rightarrow Y = 2 \times 25 = 50\\\\55 = \frac{{Z + Y}}{2} \Rightarrow 110 = Z + 50 \Rightarrow Z = 60\\\\\alpha = \frac{{Z - Y}}{2} = \frac{{60 - 50}}{2} = \frac{{10}}{2} = 5\end{array}\)
تهیه کننده: امیرحسین مطلبی
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
رابطه های طولی در دایره
فصل 1 : دایره
رابطه های طولی در دایره
اگر وتر های یک دایره یکدیگر را درون دایره قطع کنند یا امتداد وتر ها یکدیگر را در خارج دایره قطع کنند بین اندازه پاره خط های ایجاد شده روابطی برقرار است که در قضیه های زیر به آنها می پردازیم.
قضیه 1
هر گاه دو وتر دلخواه AB و CD یکدیگر را درون دایره در نقطه M قطع کنند، آنگاه:
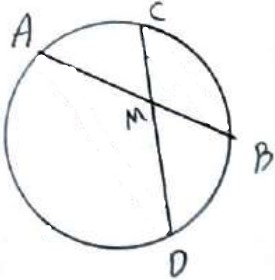
\(MA \times MB = MC \times MD\)
اثبات
از A به D و از B به C وصل می کنیم در دو مثلث ایجاد شده داریم:
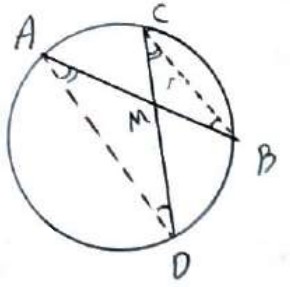
محاطی \(\hat A = \hat C = \frac{{BD}}{2}\)
محاطی \(\hat B = \hat D = \frac{{AC}}{2}\)
\(\begin{array}{l} \Rightarrow A\mathop M\limits^\Delta D \sim B\mathop M\limits^\Delta C \Rightarrow \frac{{AM}}{{MC}} = \frac{{MD}}{{MB}}\\\\ \Rightarrow AM \times MB = MC \times MD\end{array}\)
مثال
در شکل زیر مقدار X را بدست آورید.
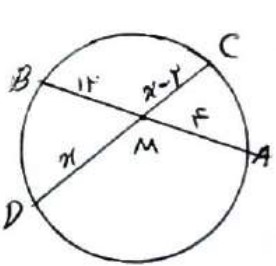
طبق روابط طولی: \(MA \times MB = MC \times MD\)
\(\begin{array}{l}4 \times 12 = \left( {x - 2} \right)x \Rightarrow 48 = {x^2} - 2x\\\\ \Rightarrow {x^2} - 2x - 48 = 0\\\\ \Rightarrow \left( {x - 8} \right)\left( {x + 6} \right) = 0 \Rightarrow x = 8\;,\;x = - 6\end{array}\)
قضیه 2
هرگاه امتداد های دو وتر AB و CD یکدیگر را خارج دایره در نقطه M قطع کنند آنگاه:
\(MA \times MB = MC \times MD\)
اثبات
از A به D و از C به B وصل می کنیم، در مثلث ایجاد شده داریم:
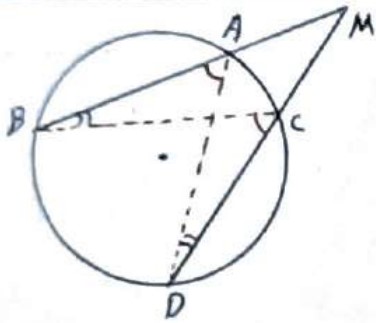
\(\begin{array}{l}\hat B = \hat D = \frac{{AC}}{2}\\\\\hat M = \hat M\\\\A\mathop M\limits^\Delta D \sim C\mathop M\limits^\Delta B \Rightarrow \frac{{MA}}{{MC}} = \frac{{MD}}{{MB}}\\\\ \Rightarrow MA \times MB = MC \times MD\end{array}\)
مثال
در شکل زیر مقدار X را بدست آورید.
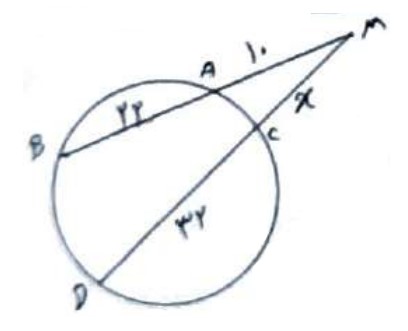
طبق روابط طولی: \(MA \times MB = MC \times MD\)
\(\begin{array}{l} \Rightarrow 10 \times 32 = x \times \left( {x + 32} \right)\\\\ \Rightarrow {x^2} + 32x - 320 = 0\\\\ \Rightarrow \left( {x + 40} \right)\left( {x - 8} \right) = 0\\\\ \Rightarrow x = - 40\;,\;x = 8\end{array}\)
که در اینجا \(x = 8\) قابل قبول است.
قضیه 3
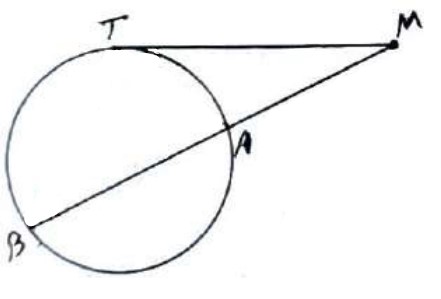
هرگاه از نقطه M خارج دایره یک مماس و یک قاطع بر دایره رسم کنیم، آنگاه مربع اندازه مماس برابر است با حاصل ضرب اندازه های دو قطعه قاطع، یعنی:
\(M{T^2} = MA \times MB\)
(به عبارت دیگر طول مماس واسطه هندسی بین دو قطعه قاطع است.)
اثبات
از T به A و B وصل می کنیم در دو مثلث \(M\mathop A\limits^\Delta T\) و \(M\mathop B\limits^\Delta T\) داریم:
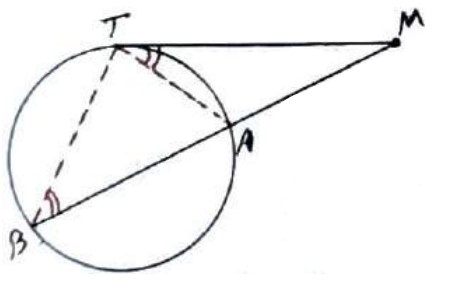
\(\begin{array}{l}\hat B = \hat T = \frac{{AT}}{2}\\\\\hat M = \hat M\\\\ \Rightarrow M\mathop A\limits^\Delta T \sim M\mathop B\limits^\Delta T \Rightarrow \frac{{MA}}{{MT}} = \frac{{MT}}{{MB}}\\\\M{T^2} = MA \times MB\end{array}\)
در شکل زیر مقادیر مجهول را بدست آورید.
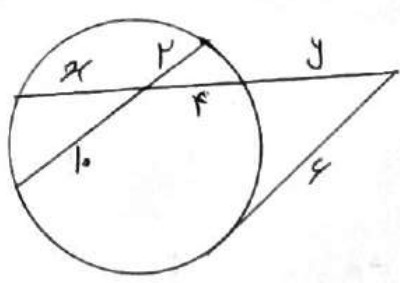
روابط طولی: \(4 \times x = 2 \times 10 \Rightarrow x = \frac{{20}}{4} = 5\)
\(\begin{array}{l}{6^2} = y\left( {y + 9} \right) \Rightarrow 36 = {y^2} + 9y\\\\ \Rightarrow {y^2} + 9y - 36 = 0\\\\ \Rightarrow \left( {y + 12} \right)\left( {y - 3} \right) = 0\\\\ \Rightarrow y = - 12\;,\;y = 3\end{array}\)
که در اینجا \(y = 3\) قابل قبول و جواب است.
تهیه کننده: امیرحسین مطلبی
رسم مماس بر دایره از نقطه ای خارج دایره
فصل 1 : دایره
رسم مماس بر دایره از نقطه ای خارج دایره
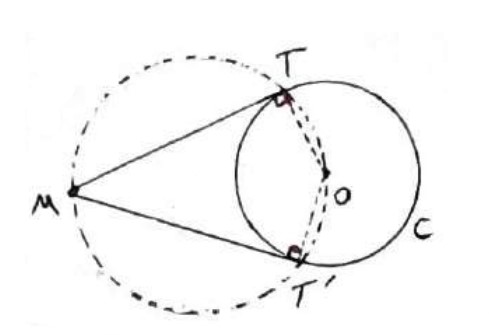
نقطه دلخواه M خارج دایره \(C\left( {O,R} \right)\) را در نظر می گیریم؛ حال دایره ای به قطر OM رسم می کنیم، به طوری که دایره \(C\left( {O,R} \right)\) را در نقاط T و \(T'\) قطع کند، در این صورت خط های MT و \(MT'\) بر دایره \(C\left( {O,R} \right)\) مماس هستند.
زیرا اگر از T و \(T'\) به O وصل کنیم، زاویه های T و \(T'\) محاطی رو به رو به قطر می باشند، پس \({90^0}\) می باشند؛ لذا چون MT و \(MT'\) بر شعاع در نقطه T و \(T'\) عمودند، پس MT و \(MT'\) مماس بر دایره می باشند.
در شکل زیر \(BC = 10\) ، \(AC = 8\) و \(AB = 12\) طول \(x = BF\) چند واحد است؟
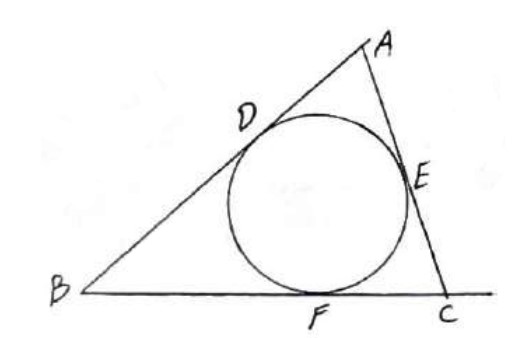
می دانیم طول 2 مماس رسم شده بر دایره از نقطه خارج دایره باهم برابر است.
\(\begin{array}{l}AD = AE\\\\BD = BF\\\\CF = CE\\\\ \Rightarrow AD + BD + CF = AE + BF + CE\\\\ \Rightarrow \left( {CF = BC - BF\;,\;AE + CE = AC} \right)\\\\ \Rightarrow AD + BC - BF = AC + BF\\\\ \Rightarrow 12 + 10 - x = 8 + x\\\\ \Rightarrow 2x = 14 \Rightarrow x = 7\end{array}\)
تهیه کننده: امیرحسین مطلبی
حالت های دو دایره نسبت به هم
فصل 1 : دایره
حالت های دو دایره نسبت به هم
پاره خطی که مرکز های دو دایره را به هم وصل می کند را خط المرکزین گویند و با d نشان می دهند.
دو دایره \(C\left( {O,R} \right)\) و \(C'\left( {O',R'} \right)\) را بر فرض \(R\rangle R'\) و \(OO' = d\) در نظر می گیریم. حالت های مختلفی که این دو دایره می توانند نسبت به هم داشته باشند به صورت زیر است:
دو دایره برون هم (متخارج)
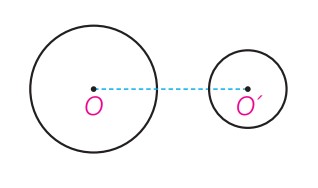
\(d\rangle R + R'\)
دو دایره مماس برون
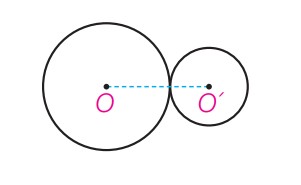
\(d = R + R'\)
دو دایره متقاطع
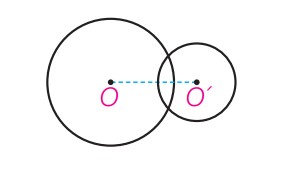
\(R - R'\langle d\langle R + R'\)
دو دایره مماس درون

\(d = R - R'\)
دو دایره متداخل
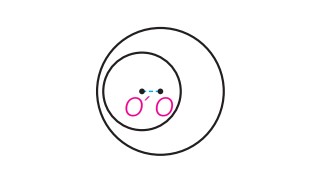
\(d\langle R - R'\)
دایره های هم مرکز
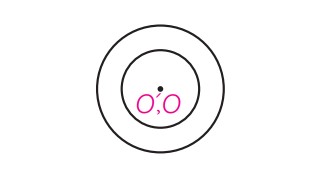
\(d = 0\)
مماس مشترک دو دایره
خطی است که بر هر دو دایره مماس است.
مماس مشترک خارجی
اگر دو دایره در یک طرف خط مماس باشند، این خط را مماس مشترک خارجی می گویند.

مماس مشترک داخلی
اگر دو دایره در طورف خط مماس باشند، این خط را مماس مشترک داخلی می گویند.

طول مماس مشترک ها به صورت زیر محاسبه می شوند:
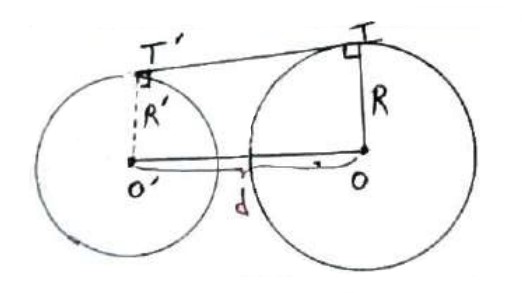
طول مماس مشترک خارجی: \(TT' = \sqrt {{d^2} - {{\left( {R - R'} \right)}^2}} \)
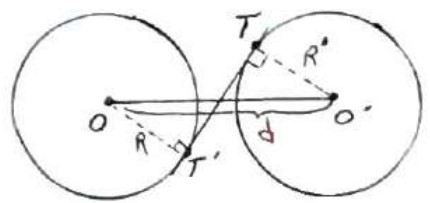
طول مماس مشترک داخلی: \(TT' = \sqrt {{d^2} - {{\left( {R + R'} \right)}^2}} \)
1 طول مماس مشترک های داخلی و خارجی دو دایره \(C\left( {O,7} \right)\) و \(C'\left( {O',1} \right)\) را با فرض \(OO' = 10\) بدست آورید.
\(OO' = d = 10\)
طول مماس مشترک خارجی:
\(\begin{array}{l}TT' = \sqrt {{d^2} - {{\left( {R - R'} \right)}^2}} = \sqrt {{{10}^2} - {{\left( {7 - 1} \right)}^2}} \\\\ \Rightarrow \sqrt {100 - 36} = \sqrt {64} = 8\end{array}\)
طول مماس مشترک داخلی:
\(\begin{array}{l}TT' = \sqrt {{d^2} - {{\left( {R + R'} \right)}^2}} = \sqrt {{{10}^2} - {{\left( {7 + 1} \right)}^2}} \\\\ \Rightarrow \sqrt {100 - 64} = \sqrt {36} = 6\end{array}\)
2 طول خط المرکزین دو دایره مماس درون 2 سانتی متر و مساحت ناحیه محدود بین آنها \(16\pi \) سانتی متر مربع است. طول و شعاع های دو دایره را بدست آورید.
\(\begin{array}{l}OO' = 2 \Rightarrow R - R' = 2\\\\S - S' = \pi {R^2} - \pi {{R'}^2} = 16\pi \\\\ \Rightarrow {R^2} - {{R'}^2} = 16\\\\ \Rightarrow \left( {R - R'} \right)\left( {R + R'} \right) = 16\\\\ \Rightarrow 2\left( {R + R'} \right) = 16 \Rightarrow \left( {R + R'} \right) = 8\\\\R - R' = 2\\\\R + R' = 8\\\\ \Rightarrow R = 5\;,\;R' = 3\end{array}\)
تهیه کننده: امیرحسین مطلبی
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
چند ضلعی محاطی
فصل 1 : دایره
چند ضلعی محاطی
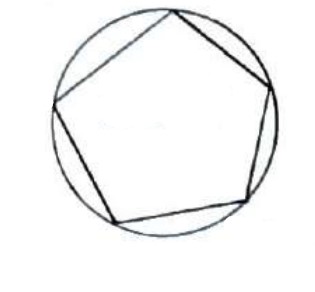
یک چند ضلعی را محاطی (محاط در دایره) می گوییم هرگاه تمام راس های آن روی محیط یک دایره باشند. (در این صورت دایره را، دایره محیطی آن چند ضلعی می نامیم.)
مثال
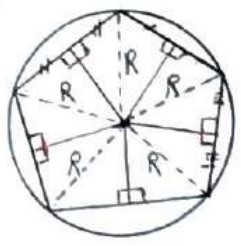
ثابت کنید مرکز دایره محیطی یک چند ضلعی، نقطه همرسی عمود منصف های همه اضلاع آن می باشد.
اثبات
واضح است که اگر نقطه O مرکز دایره محیطی چند ضلعی باشد، فاصله آن از تمام راس ها همواره برابر با شعاع دایره محیطی (R) است. بنابراین، این نقطه از دو سر هر ضلع چند ضلعی به یک فاصله است و لذا روی عمود منصف هر کدام از اضلاع قرار دارد.
عکس مطلب بالا نیز به طور مشابه اثبات می شود.
یعنی اگر به مرکز نقطه همرسی عمود منصف های اضلاع یک چند ضلعی دایره ای رسم کنیم، این دایره از تمام راس های چند ضلعی می گذرد.
در نتیجه یک چند ضلعی، محاطی است اگر و فقط اگر عمود منصف های همه اضلاع آن در یک نقطه همرس باشند.
تهیه کننده: امیرحسین مطلبی
چند ضلعی محیطی
فصل 1 : دایره
چند ضلعی محیطی
یک چند ضلعی را محیطی (محیط بر دایره) می گوییم، هر گاه تمام ضلع های آن بر یک دایره مماس باشند. (در اینصورت دایره را، دایره محاطی آن چند ضلعی می نامیم.)
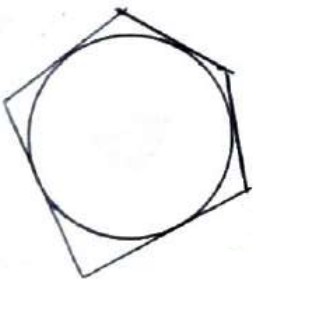
هر نقطه روی نیم ساز هر زاویه، از دو ضلع آن زاویه به یک فاصله است و برعکس اگر نقطه ای از دو ضلع یک زاویه به یک فاصله باشد، روی نیم ساز آن زاویه است.
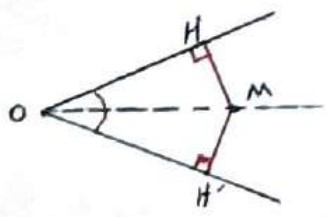
\(MH = MH'\)
مثال
ثابت کنید مرکز دایره محاطی یک چند ضلعی، نقطه همرسی نیم ساز های داخلی همه زاویه های آن می باشد.
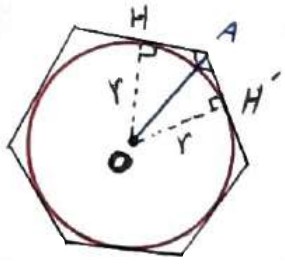
اثبات
واضح است که اگر نقطه O مرکز دایره محاطی چند ضلعی باشد، فاصله آن از تمام ضلع ها برابر با شعاع دایره محاطی (r) است.
توجه کنید که اگر از نقطه O به هر نقطه تماس وصل کنیم، شعاع در نقطه تماس بر خط مماس یعنی بر چند ضلعی، عمود است و لذا فاصله O از آن ضلع را نشان می دهد.
بنابراین این نقطه از دو ضلع هر زاویه داخلی چند ضلعی به یک فاصله است و در نتیجه روی نیمساز داخلی هر زاویه داخلی چند ضلعی قرار دارد.
یک چند ضلعی محیطی است اگر و تنها اگر همه نیم ساز های زاویه های داخلی آن در یک نقطه همرس باشند، این نقطه مرکز دایره محاطی چند ضلعی است.
اگر S و 2P به ترتیب مساحت و محیط یک چند ضلعی محیطی و r شعاع دایره محاطی آن باشد، آنگاه: \(S = rP\)
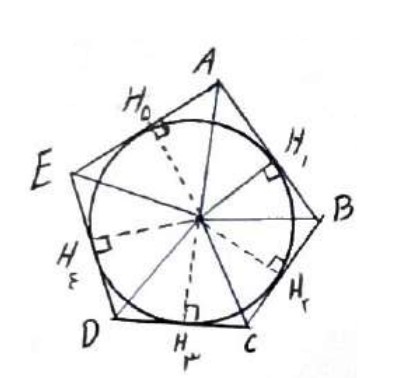
اثبات
با توجه به شکل
مساحت چند ضلعی برابر است با مجموع مساحت های مثلث های داخل
\(\begin{array}{l}{S_T} = {S_{A\mathop O\limits^\Delta B}} + {S_{B\mathop O\limits^\Delta C}} + {S_{C\mathop O\limits^\Delta D}} + {S_{D\mathop O\limits^\Delta E}} + {S_{E\mathop O\limits^\Delta A}}\\\\{S_T} = \left( {\frac{1}{2}O{H_1} \times AB} \right) + \left( {\frac{1}{2}O{H_2} \times BC} \right) + \left( {\frac{1}{2}O{H_3} \times DC} \right) + \left( {\frac{1}{2}O{H_4} \times DE} \right) + \left( {\frac{1}{2}O{H_5} \times AE} \right)\\\\ \Rightarrow O{H_1} = O{H_2} = \cdots = r\\\\ \Rightarrow {S_T} = r\left( {\frac{{AB + BC + DC + DE + AE}}{2}} \right) = rP\end{array}\)
تهیه کننده: امیرحسین مطلبی
دایره محیطی مثلث
فصل 1 : دایره
دایره محیطی مثلث
دایره ای که از سه راس یک مثلث می گذرد، دایره محیطی مثلث نامیده می شود. (مرکز دایره محیطی مثلث نقطه همرسی عمود منصف است.)
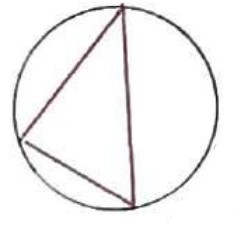
مثال
ثابت کنید مثلث همواره محاطی است.
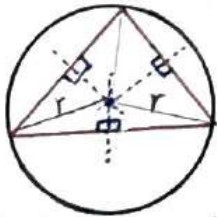
اثبات
می دانیم سه عمود منصف ضلع های هر مثلث همرس می باشند و این نقطه همرسی تنها نقطه ای است که از سه راس یک مثلث به یک فاصله است، پس اگر دایره ای به مرکز نقطه تلاقی سه عمود منصف و به شعاع فاصله این نقطه تا یک راس رسم کنیم، این دایره از هر سه راس مثلث می گذرد. (دایره محیطی مثلث) در نتیجه مثلث همواره محاطی است.
تهیه کننده: امیرحسین مطلبی
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
دایره محاطی مثلث
فصل 1 : دایره
دایره محاطی مثلث
دایره ای که بر هر سه ضلع مثلث مماس می باشد، دایره ی محاطی داخلی مثلث نامیده می شود. (مرکز دایره محاطی مثلث نقطه همرسی نیم ساز های زاویه های داخلی مثلث است.)
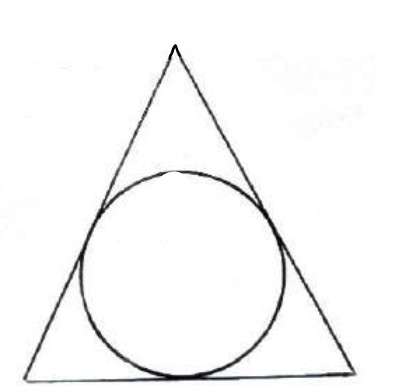
مثال
ثابت کنید مثلث همواره محیطی است.
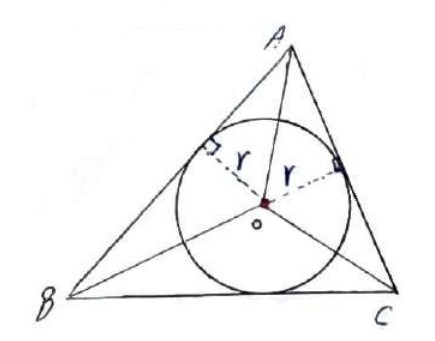
اثبات
می دانیم سه نیم ساز داخلی هر مثلث همواره در یک مثلث همرس اند، پس اگر به مرکز این نقطه همرسی و به شعاع فاصله این نقطه تا یک ضلع مثلث دایره ای رسم کنیم بر هر سه ضلع مثلث مماس خواهد شد. بنابراین مثلث همواره محیطی است.
تهیه کننده: امیرحسین مطلبی
دایره محاطی خارجی
فصل 1 : دایره
دایره محاطی خارجی
دایره ای که بر یک ضلع و امتداد دو ضلع دیگر آن مماس باشد، دایره محاطی خارجی مثلث نامیده می شود.
هر مثلث سه دایره محاطی خارجی دارد.
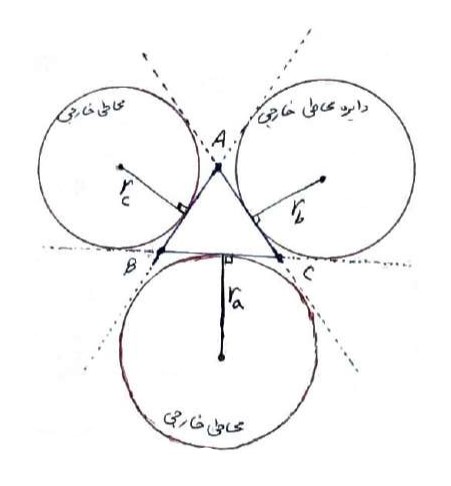
مرکز دایره محاطی خارجی مثلث، نقطه همرسی دو نیمساز خارجی و نیم ساز داخلی راس سوم است.
1 با توجه به مفهوم دایره محاطی خارجی، مثلث ABC ثابت کنید:
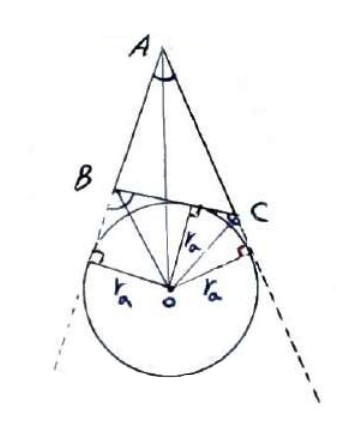
\({S_{ABC}} = {r_a}\left( {P - a} \right) \Rightarrow {r_a} = \frac{S}{{P - a}}\)
اثبات
\(\begin{array}{l}{S_{A\mathop B\limits^\Delta C}} = S = {S_{O\mathop A\limits^\Delta B}} + {S_{O\mathop A\limits^\Delta C}} - {S_{O\mathop B\limits^\Delta C}}\\\\ \Rightarrow \left( {\frac{1}{2}{r_a} \times AB} \right) + \left( {\frac{1}{2}{r_a} \times AC} \right) - \left( {\frac{1}{2}{r_a} \times BC} \right)\\\\ \Rightarrow S = {r_a}\left( {\frac{{AB + AC - BC}}{2}} \right)\\\\ \Rightarrow {r_a}\left( {\frac{{AB + AC + BC - BC - BC}}{2}} \right)\\\\ \Rightarrow {r_a}\left( {\frac{{2P - 2a}}{2}} \right) \Rightarrow {r_a} = \frac{S}{{P - a}}\end{array}\)
2 اگر \({r_a}\)، \({r_b}\) و \({r_c}\) شعاع های سه دایره محاطی خارجی مثلث \(A\mathop B\limits^\Delta C\) و r شعاع دایره محاطی داخلی باشد، نشان دهید:
\(\frac{1}{{{r_a}}} + \frac{1}{{{r_b}}} + \frac{1}{{{r_c}}} = \frac{1}{r}\)
با توجه به اینکه \({r_a} = \frac{S}{{P - a}}\) ، بنابراین:
\(\begin{array}{l}\frac{1}{{{r_a}}} + \frac{1}{{{r_b}}} + \frac{1}{{{r_c}}} = \frac{{P - a}}{S} + \frac{{P - b}}{S} + \frac{{P - c}}{S}\\\\ \Rightarrow \frac{{3P - \left( {a + b + c} \right)}}{S} = \frac{{3P - 2P}}{S} = \frac{P}{S} = \frac{1}{r}\end{array}\)
3 اگر \({h_a}\) ، \({h_b}\) و \({h_c}\) ارتفاع های نظیر سه ضلع مثلث باشند، نشان دهید:
\(\frac{1}{{{h_a}}} + \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}} = \frac{1}{r}\)
می دانیم مساحت مثلث ABC با توجه به ارتفاع های سه ضلع آن به صورت زیر بدست می آید:
\(\begin{array}{l}{S_{A\mathop B\limits^\Delta C}} = \frac{1}{2}{h_a} \times a = \frac{1}{2}{h_b} \times b = \frac{1}{2}{h_c} \times c\\\\ \Rightarrow 2S = {h_a} \times a = {h_b} \times b = {h_c} \times c\\\\ \Rightarrow {h_a} = \frac{{2S}}{a}\;,\;{h_b} = \frac{{2S}}{b}\;,\;{h_c} = \frac{{2S}}{c}\\\\ \Rightarrow \frac{1}{{{h_a}}} + \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}} = \frac{1}{{\frac{{2S}}{a}}} + \frac{1}{{\frac{{2S}}{b}}} + \frac{1}{{\frac{{2S}}{c}}}\\\\ \Rightarrow \frac{a}{{2S}} + \frac{b}{{2S}} + \frac{c}{{2S}} = \frac{{a + b + c}}{{2S}} = \frac{{2P}}{{2S}} = \frac{1}{r}\end{array}\)
تهیه کننده: امیرحسین مطلبی
چهار ضلعی های محاطی و محیطی
فصل 1 : دایره
چهار ضلعی های محاطی و محیطی
بر خلاف مثلث، همه چند ضلعی های دیگر، لزوما محاطی و محیطی نیستند. در این بخش به شرایط محاطی و یا محیطی بودن چهار ضلعی می پردازیم.
قضیه 1
یک چهار ضلعی محاطی است اگر و فقط اگر دو زاویه مقابل آن مکمل باشد.
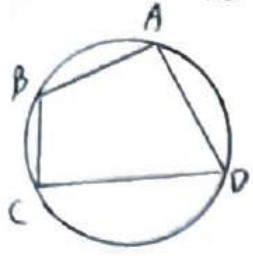
فرض می کنیم ABCD محاطی است.
حکم: \(\begin{array}{l}\hat A + \hat C = 180\\\\\hat B + \hat D = 180\end{array}\)
اثبات
\(\begin{array}{l}\hat A = \frac{{BCD}}{2}\\\\\hat C = \frac{{BAD}}{2}\\\\ \Rightarrow \hat A + \hat C = \frac{{BCD + BAD}}{2} = \frac{{360}}{2} = {180^0}\\\\\hat B = \frac{{ADC}}{2}\\\\\hat D = \frac{{ABC}}{2}\\\\ \Rightarrow \hat B + \hat D = \frac{{ADC + ABC}}{2} = \frac{{360}}{2} = {180^0}\end{array}\)
مثال
با توجه به شکل زیر اندازه X و Y را پیدا کنید.
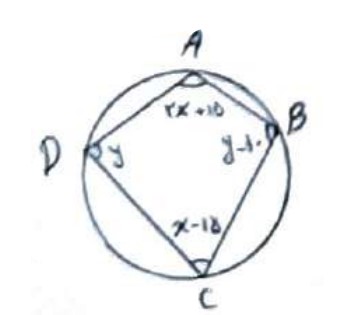
چون چهار ضلعی ABCD محاطی است، زوایای رو به رو مکمل یکدیگرند:
\(\begin{array}{l}\hat A + \hat C = 180 \Rightarrow 2x + 15 + x - 15 = 180\\\\ \Rightarrow 3x = 180 \Rightarrow x = 60\\\\\hat B + \hat D = 180 \Rightarrow y - 10 + y = 180\\\\ \Rightarrow 2y = 190 \Rightarrow y = 95\end{array}\)
قضیه 2
در یک چهار ضلعی محیطی مجموع اندازه های دو ضلع مقابل، برابر مجموع اندازه های دو ضلع مقابل دیگر است. (عکس قضیه نیز برقرار است.)
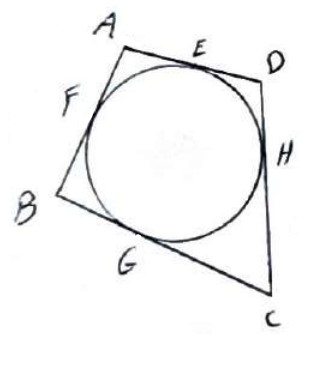
حکم: \(AB + CD = AD + BC\)
اثبات
قبلا دیدیم از هر نقطه بیرون دایره، دو مماس بر دایره رسم کنیم، اندازه های این دو مماس برابرند.
\(\begin{array}{l}AF = AE\\\\BF = BG\\\\CH = CG\\\\DH = ED\\\\ \Rightarrow AF + BF + CH + DH = AE + ED + BG + CG\\\\ \Rightarrow AB + CD = AD + BC\end{array}\)
چند ضلعی منتظم
یک چند ضلعی محدب را منتظم گوییم هر گاه تمام ضلع های آن هم اندازه و تمام زاویه های آن نیز هم اندازه باشند.
هر چند ضلعی منتظم هم محاطی است و هم محیطی.
1 فرض کنیم اندازه ضلع چهارم برابر x باشد، پس اندازه های اضلاع چهارضلعی به ترتیب 7، 11، 16 و x است. اندازه ضلع مجهول را بدست آورید.
طبق قضیه: \(x + 11 = 16 + 7 \Rightarrow x = 23 - 11 = 12\)
2 ثابت کنید یک ذوزنقه محاطی است، اگر و فقط اگر متساوی الساقین باشد.
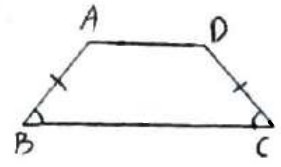
فرض کنیم ذوزنقه ABCD متساوی الساقین باشد. (\(AB = CD\;,\;AD\parallel BC\) )
نشان می دهیم محاطی است یعنی زاویه های مقابل مکمل اند. (\(\hat A + \hat C = \hat B + \hat D = {180^0}\) )
\(\begin{array}{l}ABCD \Rightarrow \hat B = \hat C\\\\AD\parallel BC \Rightarrow \hat A + \hat B = {180^0}\\\\ \Rightarrow \hat A + \hat C = {180^0} = \hat B + \hat D\end{array}\)
تهیه کننده: امیرحسین مطلبی
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
تبدیل های هندسی
فصل 2 : تبدیل های هندسی و کاربردها
تبدیل های هندسی
یکی از مفاهیم مهم در هندسه، تبدیل های هندسی است. وضعیت های مختلفی که هر شکل در اثر حرکت مجموعه نقاطش در صفحه پیدا می کند، در نتیجه یک تبدیل است.
تبدیل های مهم عبارت اند از: بازتاب، انتقال، دوران و تجانس
این تبدیل ها موقعیت یا اندازه شکل را تغییر می دهند.
تعریف تبدیل
تبدیل T در صفحه تابعی است که به هر نقطه A از صفحه دقیقا یک نقطه مانند \(A'\) از همان صفحه را نظیر کند.
\(\begin{array}{l}T:P \Rightarrow P\\\\T\left( A \right) = A'\end{array}\)
عبارت \(T\left( A \right) = A'\) یعنی \(A'\) تصویر نقطه A تحت تبدیل T است.
همچنین شکلی که از تبدیل شکل اولیه حاصل می شود را تصویر آن می نامند.
تبدیل طولپا (ایزومتری)
هر تبدیلی که طول پاره خط را حفظ می کند تبدیل طولپا یا ایزومتری نامیده می شود؛ به عبارت دیگر:
اگر \(A'\) تصویر A تحت تبدیل T باشد آنگاه \(T\left( A \right) = A'\)
اگر \(B'\) تصویر B تحت تبدیل T باشد آنگاه \(T\left( B \right) = B'\)
حال اگر T ایزومتری باشد آنگاه \(AB = A'B'\)
قضیه
هر تبدیل طولپا اندازه زاویه را حفظ می کند. (یعنی اندازه زاویه تصویر و خود زاویه مساوی است.)
اثبات
فرض کنیم T تبدیل طولپا باشد و زاویه \(A'\hat O'B'\) تصویر \(A\hat OB\) تحت این تبدیل باشد.
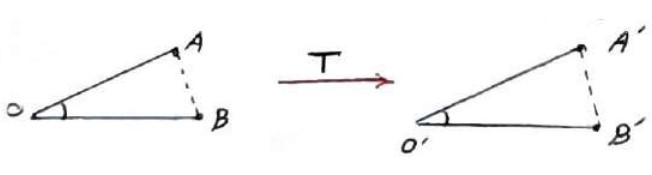
\(\begin{array}{l}T\left( A \right) = A'\\\\T\left( O \right) = O'\\\\T\left( B \right) = B'\\\\ \Rightarrow AO = A'O'\\\\BO = B'O'\\\\AB = A'B'\\\\ \Rightarrow A\mathop O\limits^\Delta B \cong A'\mathop {O'}\limits^\Delta B' \Rightarrow \hat O = \hat O'\end{array}\)
مثال
نقاط \(A\left( {3,3} \right)\) ، \(B\left( {1, - 1} \right)\) و \(C\left( { - 2,2} \right)\) راس های یک مثلث هستند.
الف مثلث و تصویرش را تحت تبدیل \(T\left( {x,y} \right) = \left( {x + 2, - y} \right)\) رسم کنید.
\(\begin{array}{l}T\left( A \right) = A'\\\\ \Rightarrow T\left( {3,3} \right) = \left( {3 + 2, - 3} \right) = \left( {5, - 3} \right)\\\\T\left( B \right) = B'\\\\ \Rightarrow T\left( {1, - 1} \right) = \left( {1 + 2,1} \right) = \left( {3,1} \right)\\\\T\left( C \right) = C'\\\\ \Rightarrow T\left( { - 2,2} \right) = \left( { - 2 + 2, - 2} \right) = \left( {0, - 2} \right)\end{array}\)
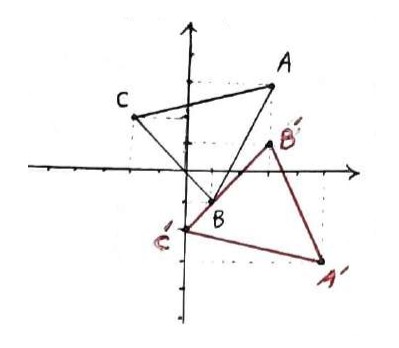
ب آیا این تبدیل طولپا است؟ چرا؟
\(\begin{array}{l}AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \\\\ \Rightarrow \sqrt {{{\left( {1 - 3} \right)}^2} + {{\left( { - 1 - 3} \right)}^2}} = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 4} \right)}^2}} \\\\ \Rightarrow \sqrt {4 + 16} = \sqrt {20} \\\\A'B' = \sqrt {{{\left( {{{x'}_B} - {{x'}_A}} \right)}^2} + {{\left( {{{y'}_B} - {{y'}_A}} \right)}^2}} \\\\ \Rightarrow \sqrt {{{\left( {3 - 5} \right)}^2} + {{\left( {1 - \left( { - 3} \right)} \right)}^2}} = \sqrt {{{\left( { - 2} \right)}^2} + {4^2}} \\\\ \Rightarrow \sqrt {4 + 16} = \sqrt {20} \end{array}\)
از اثبات بالا نتیجه می گیریم که \(AB = A'B'\) به طور مشابه \(AC = A'C'\) و \(BC = B'C'\) یعنی تبدیل T طول پاره خط را حفظ می کند، لذا طولپا است
تبدیل یافته هر خط راست یک خط راست است. لذا برای پیدا کردن تبدیل یافته یک خط کافی است تبدیل یافته دو نقطه دلخواه از آن را پیدا کرده و تصویر خط را رسم کرد و حتی معادله تصویر را بدست آورد.
نقطه تبدیل ثابت
نقطه ای که تصویر آن بر خودش منطبق باشد، نقطه ثابت تبدیل می نامیم.
تصویر خط \(x + y = 2\) را تحت تبدیل \(T\left( {x,y} \right) = \left( {x + 1,y + 2} \right)\) رسم کنید و معادله تصویر را بدست آورید.
دو نقطه دلخواه از خط را بدست می آوریم.
\(\begin{array}{l}x + y = 2\\\\x = 0 \Rightarrow y = 2 \Rightarrow A\left( {0,2} \right)\\\\y = 0 \Rightarrow x = 2 \Rightarrow B\left( {2,0} \right)\\\\T\left( A \right) = A' \Rightarrow T\left( {0,2} \right)\\\\\left( {0 + 1,2 + 2} \right) = A'\left( {1,4} \right)\\\\T\left( B \right) = B' \Rightarrow T\left( {2,0} \right)\\\\\left( {2 + 1,0 + 2} \right) = B'\left( {3,2} \right)\end{array}\)
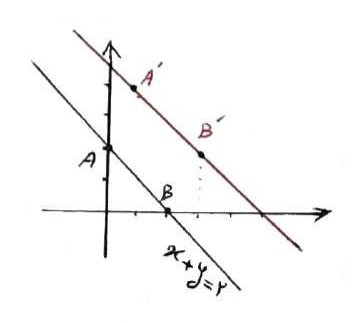
برای نوشتن معادله تصویر کافی است شیب آن را بدست آوریم:
\(\begin{array}{l}{m_{A'B'}} = \frac{{2 - 4}}{{3 - 1}} = \frac{{ - 2}}{2} = - 1\\\\y - {y_{A'}} = {m_{A'B'}}\left( {x - {x_{A'}}} \right)\\\\ \Rightarrow y - 4 = - 1\left( {x - 1} \right) \Rightarrow y = - x + 5\end{array}\)
تهیه کننده: امیرحسین مطلبی
بازتاب
فصل 2 : تبدیل های هندسی و کاربردها
بازتاب
بازتاب نسبت به خط d تبدیلی است که در آن تصویر نقطه ای مانند A نقطه \(A'\) است به طوری که d عمود منصف پاره خط \(AA'\) خواهد بود.
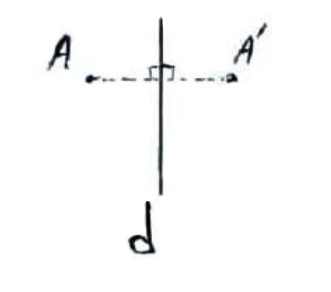
D را محور تقارن بازتاب می گویند.
برای پیدا کردن بازتاب یک نقطه مانند A نسبت به خط d کافی است از نقطه A به خط داده شده عمود کنیم سپس از پای عمود به اندازه خودش امتداد دهیم تا \(A'\) بدست آید.
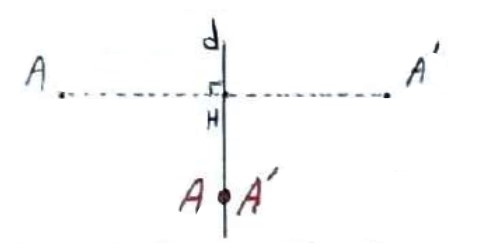
اگر نقطه ای روی محور تقارن بازتاب باشد، تصویر آن بر خودش منطبق می شود.
بازتاب نسبت به خط بی شمار نقطه ثابت تبدیل دارد، که همگی روی محور بازتاب قرار دارند.
تهیه کننده: امیرحسین مطلبی
ویژگی های بازتاب
فصل 2 : تبدیل های هندسی و کاربردها
ویژگی های بازتاب
- بازتاب شیب را لزوما حفظ نمی کند؛ مگر اینکه خط موازی محور بازتاب یا عمود بر محور بازتاب باشد.
- بازتاب نسبت به خط ایزومتری (طولپا) است یعنی اندازه پاره خط ها را تغییر نمی دهد و شکل و تصویرش همنهشت اند.
- بازتاب نسبت به خط، اندازه زاویه را تغییر نمی دهد، اما جهت زاویه و جهت شکل را تغییر می دهد.
- بازتاب نسبت به خط دارای بیشمار نقطه ثابت تبدیل است که همگی روی محور بازتاب قرار دارند.
- بازتاب، محیط و مساحت شکل را حفظ می کند.
قضیه
ثابت کنید بازتاب یک تبدیل طولپا است. (یعنی اندازه هر پاره خط و تصویرش در تبدیل بازتاب برابرند.)
اثبات
حالت های مختلف یک پاره خط نسبت به محور بازتاب را در نظر می گیریم.
الف)
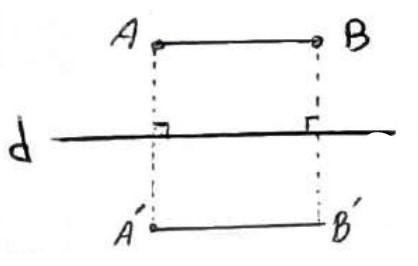
فرض: \(AB\parallel d\)
حکم: \(AB = A'B'\)
در این حالت چون دو خط عمود بر یک خط باهم موازی هستند، لذا چهارضلعی \(ABB'A'\) مستطیل می باشد و از آنجا واضح است که:
\(AB = A'B'\)
ب)
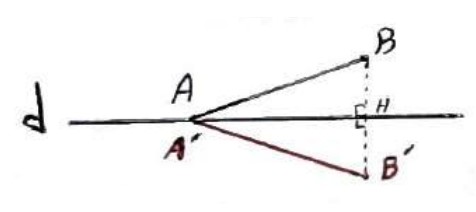
AB و d متقاطع به صورت شکل بالا باشد:
\(\begin{array}{l}BH = B'H\\\\{H_1} = {H_2} = {90^0}\\\\AH = A'H\\\\ \Rightarrow A\mathop B\limits^\Delta H \cong A'\mathop {B'}\limits^\Delta H \Rightarrow AB = A'B'\end{array}\)
ج)
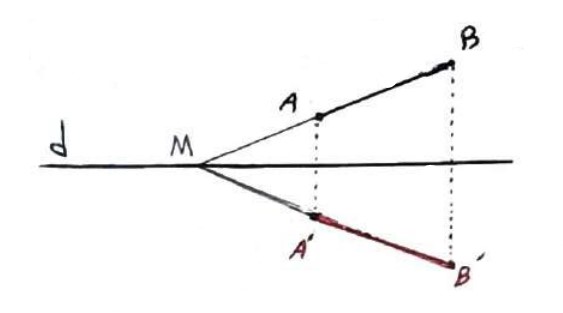
AB و d نه موازی باشد و نه متقاطع باشد:
AB را امتداد می دهیم تا خط d را در M قطع کند:
\(\begin{array}{l}MB = MB' \Rightarrow MB - MA\\\\ \Rightarrow MB' - MA' \Rightarrow AB = A'B'\end{array}\)
د)
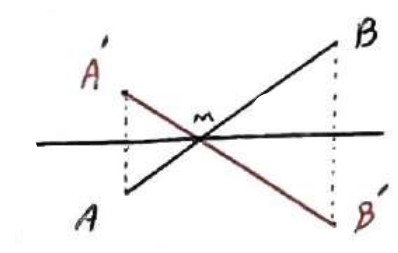
AB و d متقاطع به صورت شکل بالا باشد:
\(\begin{array}{l}AM = A'M\\\\BM = B'M\\\\ \Rightarrow AM + BM = A'M + B'M\\\\ \Rightarrow AB = A'B'\end{array}\)
تهیه کننده: امیرحسین مطلبی
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
انتقال
فصل 2 : تبدیل های هندسی و کاربردها
انتقال
یک بردار دارای ابتد، انتها، اندازه و راستا می باشد.
دو بردار مساوی
دو بردار که هم اندازه، هم راستا و هم جهت باشند دو بردار مساوی می باشند.
برای انتقال دادن یک شکل کافی است تصویر هر نقطه از شکل را به کمک بردار انتقال پیدا کنیم، مثلا نقطه A را به اندازه مختصات بردار انتقال جا به جا می کنیم، تصویر آن یعنی \(A'\) بدست می آسد.
در واقع اگر \(A'\) تصویر A به کمک بردار انتقال \(\mathop V\limits^ \to \) باشد، آنگاه \(\mathop {AA'}\limits^ \to = \mathop V\limits^ \to \)
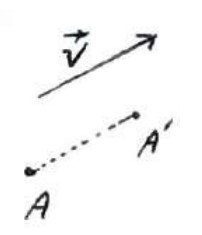
تعریف انتقال
انتقال تحت بردار \(\mathop V\limits^ \to \) تبدیلی است که در آن اگر \(A'\) تصویر A بوسیله آن تبدیل باشد، آنگاه \(\mathop {AA'}\limits^ \to = \mathop V\limits^ \to \) همچنین (\(\mathop {AA'}\limits^ \to \parallel \mathop V\limits^ \to \) )
به عبارت دیگر پاره خطی که هر نقطه را به تصویرش در انتقال وصل می کند با بردار انتقال مساوی و موازی است.
مثلث ABC به مختصات رئوس \(A\left( { - 2,2} \right)\) ، \(B\left( { - 4, - 1} \right)\) و \(C\left( { - 1,0} \right)\) را به وسیله بردار انتقال \(\mathop V\limits^ \to \left[ {\begin{array}{*{20}{c}}3\\2\end{array}} \right]\) انتقال دهید و تصویر آن را در صفحه مختصات رسم کنید.
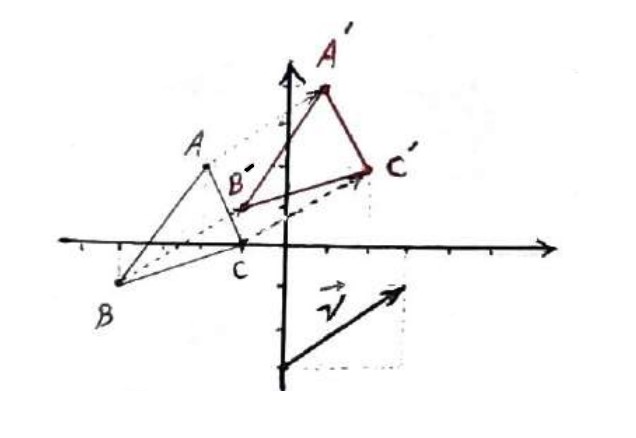
\(\mathop {AA'}\limits^ \to = \mathop {BB'}\limits^ \to = \mathop {CC'}\limits^ \to = \mathop V\limits^ \to \)
تهیه کننده: امیرحسین مطلبی
ویژگی های انتقال
فصل 2 : تبدیل های هندسی و کاربردها
ویژگی های انتقال
- انتقال ایزومتری است و انتقال یافته هر شکل با خودش همنهشت است.
- انتقال شیب خط و جهت شکل را حفظ می کند.
- انتقال اندازه زاویه را حفظ می کند.
- در انتقال بردار هایی که هر نقطه را به تصویرش وصل می کند با بردار انتقال موازی و مساوی است.
ضابطه انتقال به صورت \(T\left( {x,y} \right) = \left( {x + h,y + k} \right)\) است که در آن \(\mathop V\limits^ \to = \left[ {\begin{array}{*{20}{c}}h\\k\end{array}} \right]\) بردار انتقال می باشد.
مثال
انتقال یافته نقطه \(A\left( {1,2} \right)\) نقطه \(A'\left( {5, - 1} \right)\) است. بردار انتقال را بدست آورید.
\(\begin{array}{l}T\left( A \right) = A'\\\\T\left( {1,2} \right) = \left( {5, - 1} \right) \Rightarrow \left( {1 + h,2 + k} \right) = \left( {5, - 1} \right)\\\\1 + h = 5 \Rightarrow h = 4\\\\2 + k = - 1 \Rightarrow k = - 3\\\\ \Rightarrow \mathop V\limits^ \to = \left[ {\begin{array}{*{20}{c}}4\\{ - 3}\end{array}} \right]\end{array}\)
قضیه
ثابت کنید انتقال یک تبدیل طولپا است.
حکم: \(AB = A'B'\)
اثبات
حالت های مختلفی برای پاره خط AB و بردار انتقال \(\mathop V\limits^ \to \) در نظر می گیریم.
الف)
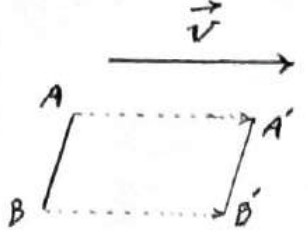
اگر AB با بردار انتقال موازی نباشد در این صورت در چهارضلعی \(AA'BB'\) داریم:
\(\mathop V\limits^ \to \;,\;AA'\;,\;BB'\) مساوی و موازی هستند بنابراین چهارضلعی \(AA'BB'\) متوازی الاضلاع است و در نتیجه:
\(AB = A'B'\)
ب)
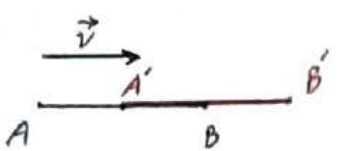
اگر \(AB\parallel \mathop V\limits^ \to \) و \(AB\rangle \mathop V\limits^ \to \)
\(\begin{array}{l}AB = AA' + A'B\\\\A'B' = A'B + BB'\\\\AA' = BB' = \mathop V\limits^ \to \\\\ \Rightarrow AB = A'B'\end{array}\)
پ)
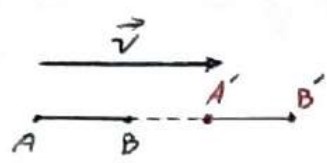
اگر \(\mathop {AB}\limits^ \to \parallel \mathop V\limits^ \to \) و \(\mathop {AB}\limits^ \to \langle \mathop V\limits^ \to \)
\(\begin{array}{l}AB = AA' - BA'\\\\A'B' = BB' - BA'\\\\AA' = BB' = \mathop V\limits^ \to \\\\ \Rightarrow AB = A'B'\end{array}\)
در انتقال تحت بردار \(\mathop V\limits^ \to \) هیچ نقطه ثابت تبدیل وجود ندارد.
در شکل زیر، پاره خط های AD و BE و CF مساوی و موازی اند، ثابت کنید \(\mathop {ABC}\limits^\Delta \cong \mathop {DEF}\limits^\Delta \)
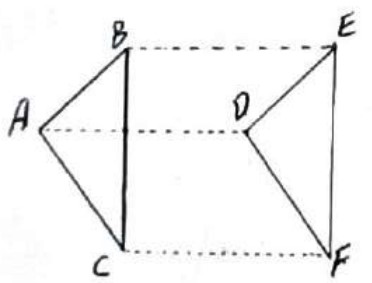
چون سه بردار AD، BE و CF مساوی و موازی اند لذا تحت یک بردار انتقال مانند بردار \(\mathop {AD}\limits^ \to \) داریم:
\(\begin{array}{l}A \Rightarrow D\\\\B \Rightarrow E\\\\C \Rightarrow F\\\\ \Rightarrow AB = DE\\\\AC = DF\\\\BC = EF\\\\ \Rightarrow \mathop {ABC}\limits^\Delta \cong \mathop {DEF}\limits^\Delta \end{array}\)
تهیه کننده: امیرحسین مطلبی
دوران
فصل 2 : تبدیل های هندسی و کاربردها
دوران
در سال های گذشته دیدید که برای دوران دادن هر شکل به مرکز دوران O و به اندازه زاویه \(\alpha \)، کتفی است هر نقطه از شکل مانند نقطه P را به مرکز دوران یعنی O وصل کنیم؛ سپس در جهت خواسته شده به کمک OP زاویه ای برابر \(\alpha \) رسم و روی ضلع دیگر این زاویه پاره خطی به اندازه OP جدا می کنیم، تا نقطه \(P'\) بدست آید.
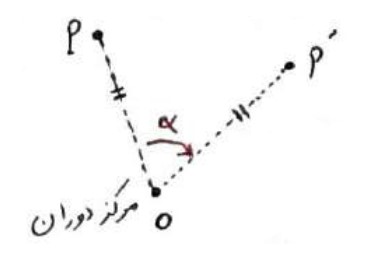
دوران R به مرکز نقطه ثابت O و زاویه \(\alpha \) تبدیلی از صفحه است که در آن \(A'\) تصویر نقطه A (در دوران به مرکز O و زاویه \(\alpha \)) است هر گاه دو شرط زیر برقرار باشد:
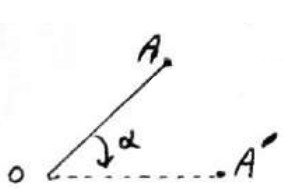
1) \(OA = OA'\)
2) \(A\hat OA = \alpha \)
مرکز دوران نقطه ثابت دوران است. (یعنی مرکز دوران تنها نقطه ای است که تصویرش تحت یک دوران خودش است.)
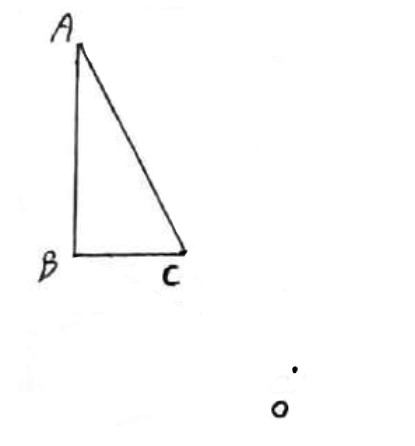
مثلث ABC زیر را حول مرکز O و به اندازه 90 درجه در جهت حرکت عقربه های ساعت دوران داده و تصویر آن را رسم کنیم.
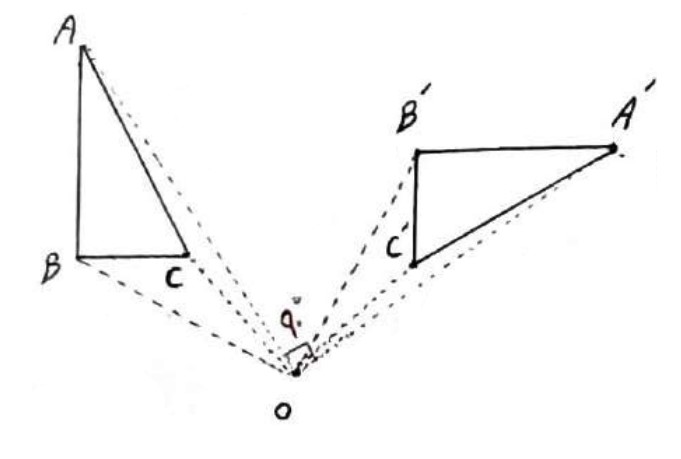
الف آیا این تبدیل موقعیت شکل اولیه را حفظ می کند؟
خیر.
ب آیا این تبدیل اندازه ها را حفظ می کند؟
بله، اندازه ها را حفظ می کند.
پ آیا این تبدیل جهت شکل را حفظ می کند؟
بله، جهت شکل را حفظ می کند.
ج آیا این تبدیل شیب پاره خط ها را حفظ می کند؟
خیر
د آیا می توان زاویه دوران را طوری تعیین کنید که دوران تحت آن، شیب خط را حفظ کند؟
بله، دوران های 0، 180 و 360 درجه.
تهیه کننده: امیرحسین مطلبی
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
ویژگی های دوران
فصل 2 : تبدیل های هندسی و کاربردها
ویژگی های دوران
- دوران شیب خط را لزوما حفظ نمی کند.
- دوران ایزومتری (طولپا) است و دوران یافته شکل با خودش همنهشت است.
- دوران جهت شکل را تغییر نمی دهد.
- دوران اندازه زاویه را حفظ می کند.
مثال
زاویه \(A\hat BC = \alpha \) ، تحت دوران 60 درجه در جهت A به C حول B به زاویه \({A_1}\hat B{C_1}\) تبدیل می شود؛ زاویه \(A\hat B{C_1}\) بر حسب \(\alpha \) را بدست آورید.
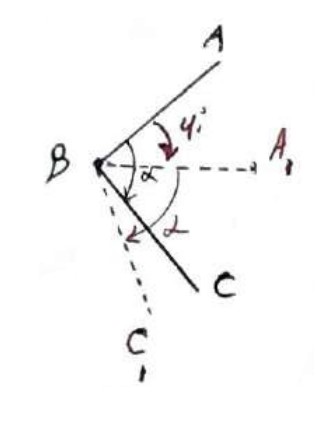
چون \(A\hat BC = \alpha \) و تحت دوران 60 درجه کل این زاویه حول نقطه B دوران یافته و زاویه \({A_1}\hat B{C_1} = \alpha \) :
\(A\hat B{C_1} = A\hat B{A_1} + {A_1}\hat B{C_1} = 60 + \alpha \)
قضیه
ثابت کنید دوران طولپا است.
حکم: \(AB = A'B'\)
اثبات
الف)
حالتی را در نظر می گیریم که مرکز دوران بر پاره خط AB و امتداد آن واقع نباشد و زاویه دوران از زاویه \(A\hat OB\) بیشتر باشد.
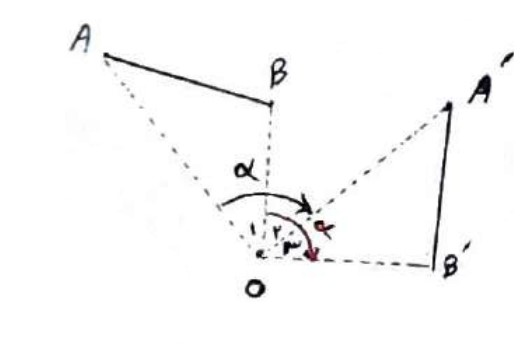
با توجه به شکل: \(\alpha = {O_1} + {O_2} = {O_2} + {O_3} \Rightarrow {\hat O_1} = {\hat O_3}\)
\(\begin{array}{l}{{\hat O}_1} = {{\hat O}_3}\\\\OA = OA'\\\\OB = OB'\\\\ \Rightarrow O\mathop A\limits^\Delta B \cong O\mathop {A'}\limits^\Delta B' \Rightarrow AB = A'B'\end{array}\)
ب)
حالتی را در نظر می گیریم که O روی امتداد AB باشد.
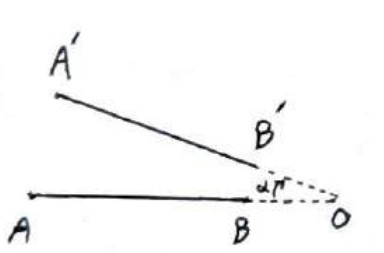
\(\begin{array}{l}AB = AO - OB\\\\A'B' = A'O - OB'\\\\OA = OA'\;,\;OB = OB'\\\\ \Rightarrow AB = A'B'\end{array}\)
نقطه \(A'\) تصویر نقطه A در بازتاب نسبت به خط L است. اگر \(AA' = 16\) و نقطه O روی خط L و \(OA = 10\) باشد، فاصله نقطه A از خط \(OA'\) چقدر است؟
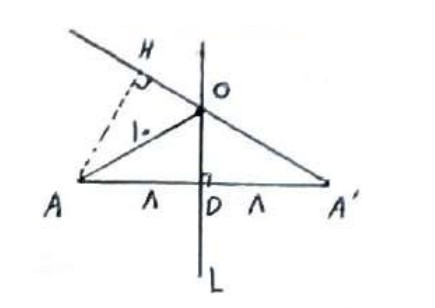
چون بازتاب طولپا است: \(OA' = OA = 10\)
\(\begin{array}{l}O{A^2} = A{D^2} + O{D^2} \Rightarrow {10^2} = {8^2} + O{D^2}\\\\ \Rightarrow O{D^2} = 100 - 64 = 36 \Rightarrow OD = 6\\\\{S_{O\mathop A\limits^\Delta A'}} = \frac{1}{2}OD \times AA' = \frac{1}{2}6 \times 16 = 48\\\\{S_{O\mathop A\limits^\Delta A'}} = \frac{1}{2}AH \times OA' = \frac{1}{2}AH \times 10 = 5AH\\\\5AH = 48 \Rightarrow AH = \frac{{48}}{5}\end{array}\)
تهیه کننده: امیرحسین مطلبی
تجانس
فصل 2 : تبدیل های هندسی و کاربردها
تجانس
یک تبدیل هندسی در صفحه است که تحت آن شکل های مشابه ایجاد می شود؛ در تجانس ابعاد شکل به یک نسبت ثابت بزرگ یا کوچک می شود، این نسبت ثابت را نسبت تجانس (مقیاس) می نامند و با نماد k نشان می دهند.
تجانس به مرکز O و نسبت k تبدیلی است که در آن \(M'\) مجانس M است هر گاه:
1) نقاط O، M و \(M'\) روی یک امتداد باشند.
2) \(OM' = \left| k \right|.OM\)
ضابطه تبدیل تجانس
تجانس به مرکز \(O\left( {0,0} \right)\) و نسبت k به صورت \(D\left( {x,y} \right) = \left( {kx\;,\;ky} \right)\) می باشد.
مثال
نقاط \(A\left( {1,2} \right)\) ، \(B\left( {0,1} \right)\) ، \(C\left( {1,0} \right)\) و \(D\left( {2,1} \right)\) راس های یک مربع هستند؛ مربع ABCD و تصویر مجانس آن را با در نظر گرفتن \(O\left( {0,0} \right)\) به عنوان مرکز تجانس و \(k = 2\) نسبت تجانس رسم کنید.
\(\begin{array}{l}A\left( {1,2} \right) \Rightarrow A'\left( {2,4} \right)\\\\B\left( {0,1} \right) \Rightarrow B'\left( {0,2} \right)\\\\C\left( {1,0} \right) \Rightarrow C'\left( {2,0} \right)\\\\D\left( {2,1} \right) \Rightarrow D'\left( {4,2} \right)\end{array}\)
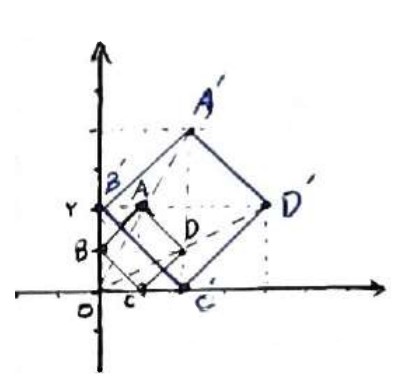
در تجانس به مرکز مبدا مختصات و نسبت k اگر \(M'\left( {x',y'} \right)\) تصویر \(M\left( {x,y} \right)\) باشد آنگاه:
\(\begin{array}{l}x' = kx\\\\y' = ky\\\\ \Rightarrow M'\left( {x',y'} \right) = \left( {kx,ky} \right)\end{array}\)
هرگاه بخواهیم در تجانس به مرکز O و نسبت k، تصویر نقطه ای مانند M را پیدا کنیم، ابتدا از M به O وصل کرده و سپس با توجه به رابطه \(OM' = KOM\) و علامت k، فقط \(M'\) در جهت OM یا خلاف جهت آن مشخص می شود.
1 اگر k مثبت باشد M و در \(M'\) یک طرف O قرار می گیرند.
2 اگر k منفی باشد M و \(M'\) در دو طرف O قرار می گیرند.
3 اگر \(M'\) مجانس M در تجانس به مرکز O و نسبت k باشد، آنگاه M نیز مجانس \(M'\) در تجانس به مرکز O و نسبت \(\frac{1}{k}\) است؛ زیرا:
\(OM' = k.OM \Rightarrow OM = \frac{1}{k}.OM'\)
تهیه کننده: امیرحسین مطلبی
ویژگی های تجانس
فصل 2 : تبدیل های هندسی و کاربردها
ویژگی های تجانس
- اگر در تجانس \(k > 0\) باشد، آن را تجانس مستقیم می نامند.
- اگر در تجانس \(k < 0\) باشد آن را تجانس معکوس می نامند.
- اگر \(\left| k \right| < 1\) باشد تصویر شکل کوچک تر می شود و آن را انقباض می نامیم.
- اگر \(\left| k \right| > 1\) باشد تصویر شکل بزرگ تر می شود و آن را انبساط می نامیم.
- اگر \(\left| k \right| = 1\) باشد، تجانس ایزومتری (طولپا) است.
- خطوطی که هر نقطه را به تصویر مجانسش وصل می کند در مرکز تجانس همرس می باشند.
- تجانس جهت شکل را تغییر نمی دهد.
- تجانس شیب خط را حفظ می کند.
- تجانس تبدیل طولپا نمی باشد.
- تجانس اندازه زاویه را حفظ می کند.
قضیه 1
ثابت کنید تجانس شیب خط را حفظ می کند.
اثبات
تجانس D به مرکز O و نسبت \(k > 0\) و خط AB را در 2 حالت در نظر می گیریم.
الف)
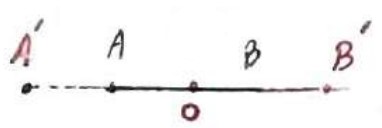
نقطه O روی AB باشد. در این صورت اگر \(A'\) و \(B'\) مجانس های A و B باشند روی خط AB قرار می گیرند، لذا \(A'B'\) روی AB واقع است و شیب خط تغییری نمی کند.
ب)
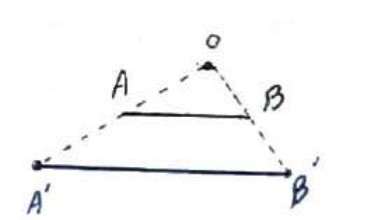
فقط O روی AB نباشد.
در این صورت اگر \(A'\) و \(B'\) مجانس های A و B باشند، طبق تعریف تجانس داریم:
\(\begin{array}{l}OA' = k.OA\\\\OB' = k.OB\\\\ \Rightarrow \frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = k \Rightarrow AB\parallel A'B'\end{array}\)
قضیه 2
ثابت کنید تجانس اندازه زاویه را حفظ می کند.
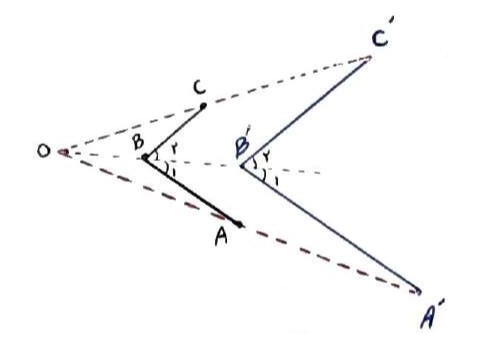
می دانیم تجانس شیب خط را حفظ می کند لذا خط و تصویر تجانس موازی اند.
\(\begin{array}{l}AB\parallel A'B' \Rightarrow {{\hat B}_1} = {{\hat B'}_1}\\\\BC\parallel B'C' \Rightarrow {{\hat B}_2} = {{\hat B'}_2}\\\\ \Rightarrow {{\hat B}_1} + {{\hat B}_2} = {{\hat B'}_1} + {{\hat B'}_2} \Rightarrow \hat B = \hat B'\end{array}\)
در تجانس به مرکز O و نسبت k طول پاره خط، k برابر می شود یعنی:
\(A'B' = k.AB\)
بنابراین محیط با ضریب k تغییر می کند:
\(P' = kP\)
مساحت با ضریب \({k^2}\) تغییر می کند:
\(S' = {k^2}.S\)
در واقع برقراری خواص بالا به این دلیل است که تصویر هر شکل در یک تجانس با خود شکل متشابه است.
دو شکل متشابه الزاما متجانس نیستند، مگر اینکه اضلاع آنها، نظیر به نظیر موازی باشند.
1 اگر \(A\left( {1,3} \right)\) ، \(B\left( {3,3} \right)\) و \(C\left( {3,0} \right)\) رئوس یک مثلث باشند، مثلث و تصویر مجانس آن را تحت تجانس مرکز \(O\left( {0,0} \right)\) و نسبت \(k = 2\) رسم کنید. طول پاره خط ها و محیط ها و مساحت ها را باهم مقایسه کنید.
\(\begin{array}{l}A\left( {1,3} \right) \Rightarrow A'\left( {2,6} \right)\\\\B\left( {3,3} \right) \Rightarrow B'\left( {6,6} \right)\\\\C\left( {3,0} \right) \Rightarrow C'\left( {6,0} \right)\end{array}\)
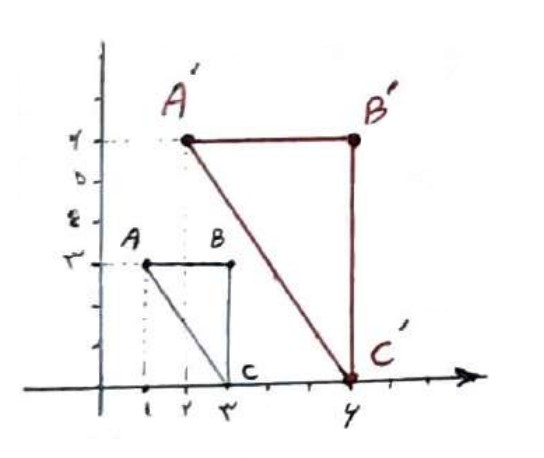
\(\begin{array}{l}AB = 2\\\\BC = 3\\\\ \Rightarrow AC = \sqrt {13} \\\\A'B' = 4\\\\B'C' = 6\\\\ \Rightarrow A'C' = 2\sqrt {13} \\\\{P_{A\mathop B\limits^\Delta C}} = 2 + 3 + \sqrt {13} = 5\sqrt {13} \\\\{P_{A'\mathop {B'}\limits^\Delta C'}} = 4 + 6 + 2\sqrt {13} = 2\left( {5 + \sqrt {13} } \right)\\\\ \Rightarrow P' = 2P\\\\{S_{A\mathop B\limits^\Delta C}} = \frac{1}{2}\left( {3 \times 2} \right) = 3\\\\{S_{A'\mathop {B'}\limits^\Delta C'}} = \frac{1}{2}\left( {6 \times 4} \right) = 12 = {2^2} \times 3\\\\ \Rightarrow S' = {2^2} \times S\end{array}\)
2 اگر n ضلعی \({A'_1}{A'_2} \cdots {A'_n}\) مجانس n ضلعی \({A_1}{A_2} \cdots {A_n}\) به مرکز O و به نسبت k باشد نشان دهید، این دو n ضلعی باهم متشابه اند.
\(\begin{array}{l}O{{A'}_1} = k.O{A_1}\\\\O{{A'}_2} = k.O{A_2}\\ \vdots \\O{{A'}_n} = k.O{A_n}\\\\ \Rightarrow \frac{{O{{A'}_1}}}{{O{A_1}}} = \frac{{O{{A'}_2}}}{{O{A_2}}} = \cdots = \frac{{O{{A'}_n}}}{{O{A_n}}} = k\end{array}\)
بنابراین همه اضلاع نظیر به نظیر متناسب اند و لذا طبق تعریف تشابه، این دو شکل متشابه اند.
تهیه کننده: امیرحسین مطلبی
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
تبدیل همانی
فصل 2 : تبدیل های هندسی و کاربردها
تبدیل همانی
تبدیلی که هر نقطه صفحه را به خود آن نقطه نظیر می کند تبدیل همانی نامیده می شود.
به عبارت دیگر تبدیل T را همانی گوییم هرگاه به ازای هر نقطه A از صفحه P داشته باشیم:
\(T\left( A \right) = A\)
معمولا تبدیل های همانی را I نشان می دهند؛ پس:
\(I\left( A \right) = A\)
تبدیل همانی طولپا است؛ زیرا تصویر هر پاره خط بر خودش منطبق است به عبارتی:
\(\begin{array}{l}A' = I\left( A \right) = A\\\\B' = I\left( B \right) = B\\\\ \Rightarrow A'B' = AB\end{array}\)
1 آیا بازتاب می تواند همانی باشد؟
بازتاب هیچگاه تبدیل همانی نیست؛ زیرا فقط تصویر نقاطی که روی محور بازتاب قرار دارد روی خود آن نقاط هم قرار دارد و تصویر نقاطی دیگر مثل A که روی محور قرار ندارند نقاط \(A'\) می باشد که در طرف دیگر محور بازتاب قرار دارد.
2 در چه شرایطی انتقال، دوران و تجانس می توانند همانی باشند؟
اگر طول بردار انتقال صفر باشد انتقال همانی است زیرا تصویر هر نقطه بر خودش منطبق است.
اگر زاویه دوران برابر 0 یا 360 درجه باشد دوران همانی است زیرا تصویر هر نقطه بر خودش منطبق است.
اگر نسبت تجانس \(k = 1\) باشد تجانس همانی است زیرا تصویر هر نقطه بر خودش منطبق است.
3 در هر یک از تبدیل های، انتقال غیر همانی، دوران غیر همانی و تجانس غیر همانی نقاط ثابت تبدیل را در صورت وجود مشخص کنید.
انتقال غیر همانی نقطه ثابت تبدیل ندارد. (هر نقطه باید تحت یک بردار غیر صفر در صفحه بلغزد و نمی توان بر روی خودش بلغزد.)
در دوران غیر همانی فقط مرکز دوران نقطه ثابت تبدیل است.
در تجانس غیر همانی فقط مرکز تجانس نقطه ثابت تبدیل است.
تهیه کننده: امیرحسین مطلبی
کاربرد تبدیل ها
فصل 2 : تبدیل های هندسی و کاربردها
کاربرد های از بازتاب (قرینه یابی)
بازتاب علاوه بر شاخه های مختلف ریاضی در دیگر علوم نظیر هنر، معماری، فیزیک و ... کاربرد دارد. مثلا در فیزیک ویژگی های بازتاب همان ویژگی های آینه تخت است.
هرگاه بخواهیم شکلی را به تکه های برابر تقسیم کنیم می توانیم از بازتاب استفاده کنیم زیرا بازتاب همان قرینه یابی است.
مثال
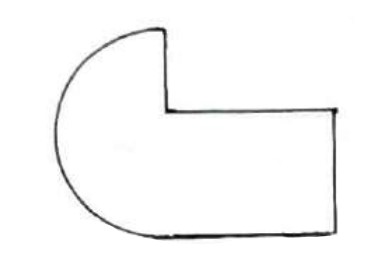
شکل زیر را به دو قسمت مساوی تقسیم کنید.
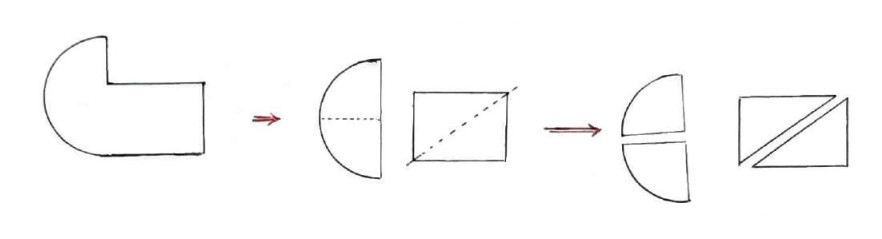
مسائل هم پیرامونی (هم محیطی)
در این گونه مسائل هدف این است که بدون اینکه محیط یک چند ضلعی تغییر کند، مساحت آن چند ضلعی را تغییر دهیم.
مثال
زمینی به شکل چند ضلعی ABCDE داریم که دور آن حصار کشیدیم، حال میخواهیم با ثابت نگه داشتن محیط و ثابت نگه داشتن تعداد اضلاع بدون اینکه اندازه حصار کشی تغییر کند مساحت زمین را افزایش دهیم. با استفاده از چه تبدیلی و چگونه این کار انجام می شود؟
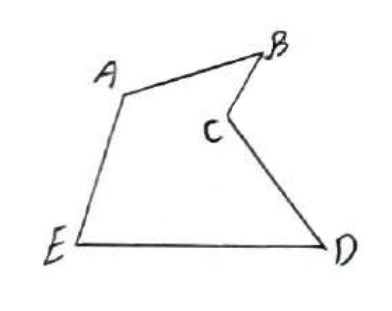
از B به D وصل می کنیم:
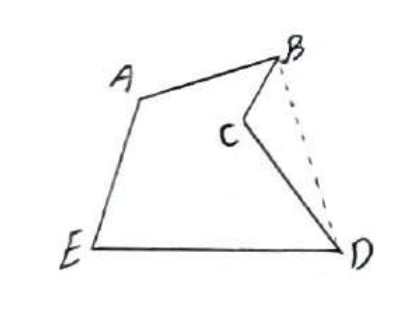
حال BD را به عنوان محور بازتاب در نظر می گیریم و تصویر نقاط B، D و C را نسبت به این محور بدست می آوریم:
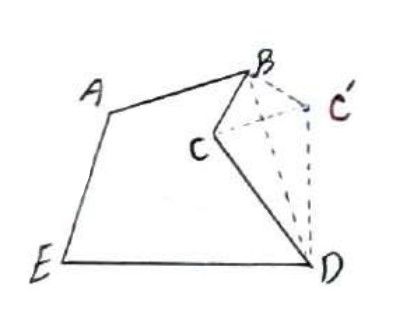
در این صورت چند ضلعی \(ABC'DE\) جواب مسئله است:
\(\begin{array}{l}{P_{ABC'DE}} = AB + BC' + C'D + DE + EA\\\\ \Rightarrow AB + BC + CD + DE + EA = {P_{ABCDE}}\end{array}\)
مراحل حل مسائل هم پیرامونی برای پند ضلعی های مقعر وقتی که افزایش مساحت مورد نظر باشد را تا آنجایی ادامه می دهیم که چند ضلعی محدب به دست آید.
تهیه کننده: امیرحسین مطلبی
مسائل کوتاه ترین مسیر
فصل 2 : تبدیل های هندسی و کاربردها
مسائل کوتاه ترین مسیر
نخستین بار توسط ریاضی دانی به نام هرون 150 تا 250 سال قبل از میلاد مسیح دستور پیدا کردن کوتاه ترین مسیر در شرایط خاص ارائه شد.
مثال
مردی می خواهد برای برداشتن آب از خانه به ساحل رودخانه ای که لبه ی مستقیمی دارد برود و بعد سطل آب را به اصطبل ببرد که در همان سمت رودخانه است. او از کدام نقطه از ساحل آب بردارد که مسافتی که در مجموع طی می کند کمترین حالت ممکن باشد.
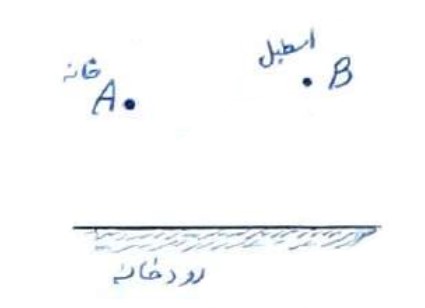
هدف این مسئله پیدا کردن نقطه ای مانند M روی خط d (ساحل) است به طوری که \(AM + MB\) کمترین مقدار ممکن باشد.
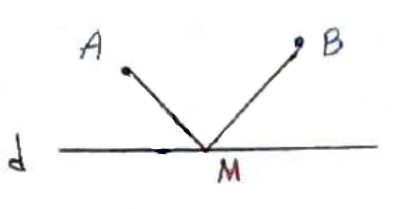
بازتاب نقطه A را نسبت به خط d پیدا کرده و آن را \(A'\) می نامیم. از \(A'\) به B وصل می کنیم، محل تلاقی این پاره خط d را M در نظر میگیریم. فقط M جواب مسئله است.
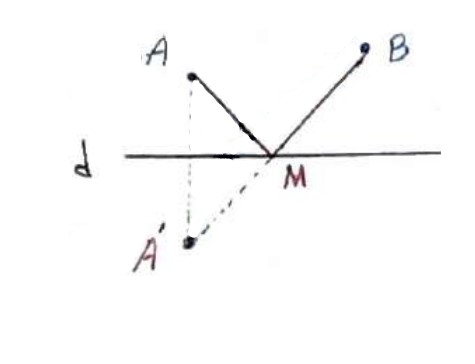
نشان می دهیم \(AM + MB\) کوتاه ترین مسیر است.
فرض می کنیم N نقطه دلخواه روی خط d باشد، آنگاه طبق نامساوی مثلث در \(AN'B\) آنگاه:
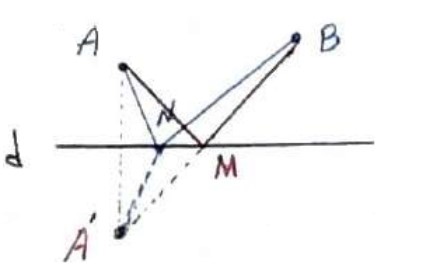
\(\begin{array}{l}A'B < A'N + NB\\\\A'M + MB < A'N + NB\\\\ \Rightarrow AM + MB < AN + NB\end{array}\)
تهیه کننده: امیرحسین مطلبی
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
روابط طولی در مثلث قائم الزاویه
فصل 3 : روابط طولی در مثلث
روابط طولی در مثلث قائم الزاویه
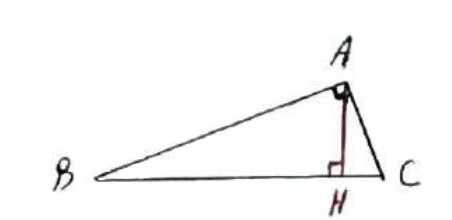
در هر مثلث قائم الزاویه، هر ضلع قائم واسطه هندسی وتر و تصویر آن ضلع بر وتر است:
1) \(A{B^2} = BC \times BH\)
2) \(A{C^2} = BC \times CH\)
ارتفاع های وارد بر وتر واسطه هندسی قطعه های ایجاد شده، روی وتر است:
3) \(A{H^2} = BH \times CH\)
رابطه فیثاغورس:
4) \(B{C^2} = A{B^2} + A{C^2}\)
حاصل ضرب اضلاع قائمه برابر است با حاصل ضرب وتر و ارتفاع وارد بر وتر:
5) \(AB \times AC = BC \times AH\)
ثابت کنید در هر مثلث قائم الزاویه ABC که \(\hat A = {90^0}\) با ارتفاع \(AH = {h_a}\) داریم:
\(\frac{1}{{h_a^2}} = \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}\)
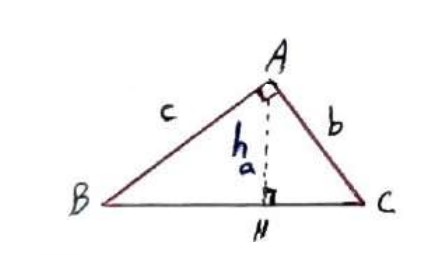
\(\begin{array}{l}\frac{1}{{{b^2}}} + \frac{1}{{{c^2}}} = \frac{{{c^2} + {b^2}}}{{{b^2}{c^2}}} = \frac{{{a^2}}}{{{b^2}{c^2}}}\\\\ \Rightarrow {\left( {\frac{a}{{bc}}} \right)^2} = {\left( {\frac{a}{{a{h_a}}}} \right)^2} = \frac{1}{{h_a^2}}\end{array}\)
تهیه کننده: امیرحسین مطلبی
قضیه سینوس ها
فصل 3 : روابط طولی در مثلث
قضیه سینوس ها
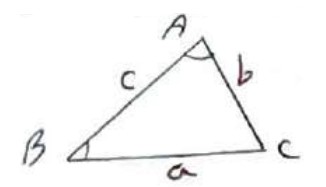
در مثلث دلخواه ABC داریم:
\(\frac{a}{{{\mathop{\rm Sin}\nolimits} A}} = \frac{b}{{{\mathop{\rm Sin}\nolimits} B}} = \frac{c}{{{\mathop{\rm Sin}\nolimits} C}} = 2R\)
اثبات:
حالت اول: \(A < {90^0}\)
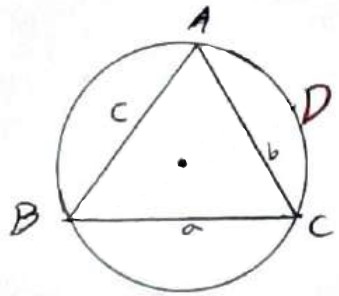
قطر BD را رسم می کنیم و D را به A وصل می کنیم. دو زاویه D و C محاطی و رو به رو به کمان AB هستند، لذا با هم برابر هستند:
\(\hat D = \hat C = \frac{{AB}}{2}\)
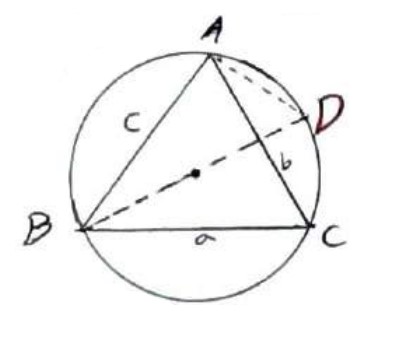
\(\begin{array}{l}\mathop {BAD}\limits^\Delta = {90^0}\\\\{\mathop{\rm Sin}\nolimits} D = \frac{c}{{BD}} \Rightarrow {\mathop{\rm Sin}\nolimits} C = \frac{c}{{BD}}\\\\ \Rightarrow \frac{c}{{{\mathop{\rm Sin}\nolimits} C}} = BD = 2R\\\\\frac{b}{{{\mathop{\rm Sin}\nolimits} B}} = 2R\;,\;\frac{a}{{{\mathop{\rm Sin}\nolimits} A}} = 2R\\\\ \Rightarrow \frac{a}{{{\mathop{\rm Sin}\nolimits} A}} = \frac{b}{{{\mathop{\rm Sin}\nolimits} B}} = \frac{c}{{{\mathop{\rm Sin}\nolimits} C}} = 2R\end{array}\)
حالت دوم: \(A > {90^0}\)
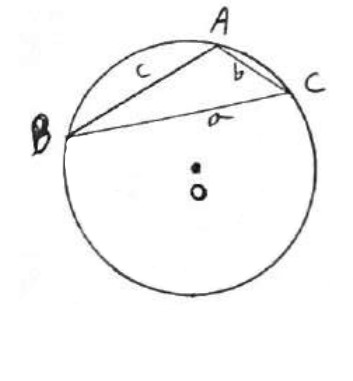
نقطه دلخواه \(A'\) روی کمان BC را به B و C وصل می کنیم.
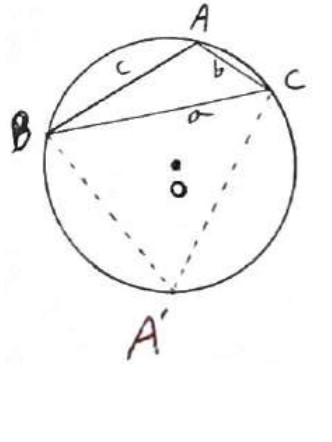
A و \(A'\) مکمل یکدیگرند یعنی \(\hat A + \hat A' = {180^0}\) زیرا \(ABA'C\) چهار ضلعی محاطی است پس قضایای اثبات شده زاویه های مقابل مکمل اند.
\(\begin{array}{l}\hat A + \hat A' = {180^0} \Rightarrow A > {90^0} \Rightarrow A' < {90^0}\\\\\frac{a}{{{\mathop{\rm Sin}\nolimits} A'}} = 2R\\\\ \Rightarrow {\mathop{\rm Sin}\nolimits} A = {\mathop{\rm Sin}\nolimits} \left( {180 - A'} \right) = {\mathop{\rm Sin}\nolimits} A'\\\\ \Rightarrow \frac{a}{{{\mathop{\rm Sin}\nolimits} A}} = 2R\;,\;\frac{b}{{{\mathop{\rm Sin}\nolimits} B}} = 2R\;,\;\frac{c}{{{\mathop{\rm Sin}\nolimits} C}} = 2R\end{array}\)
در مثلث ABC، \(BC = 10\) ، \(\hat A = {120^0}\) و \(AC = \frac{{10\sqrt 6 }}{3}\) مقدار شعاع دایره محیطی مثلث و اندازه زاویه های B و C را بدست آورید.
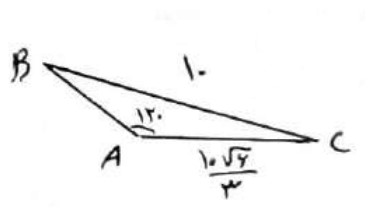
\(\begin{array}{l}\frac{a}{{{\mathop{\rm Sin}\nolimits} A}} = 2R \Rightarrow \frac{{10}}{{\frac{{\sqrt 3 }}{2}}} = 2R \Rightarrow \frac{{20}}{{\sqrt 3 }} = 2R\\\\ \Rightarrow R = \frac{{10}}{{\sqrt 3 }}\\\\\frac{b}{{{\mathop{\rm Sin}\nolimits} B}} = 2R \Rightarrow \frac{{\frac{{10\sqrt 6 }}{3}}}{{{\mathop{\rm Sin}\nolimits} B}} = 2\frac{{10}}{{\sqrt 3 }}\\\\ \Rightarrow {\mathop{\rm Sin}\nolimits} B = \frac{{10 \times 3\sqrt 2 }}{{3 \times 20}} = \frac{{\sqrt 2 }}{2} \Rightarrow \hat B = {45^0}\\\\\hat C = 180 - \left( {\hat B + \hat A} \right) = 180 - 165 = {15^0}\end{array}\)
تهیه کننده: امیرحسین مطلبی
قضیه کسینوس ها
فصل 3 : روابط طولی در مثلث
قضیه کسینوس ها
از قبل می دانیم در مثلث قائم الزاویه با داشتن دو ضلع قائمه از رابطه فیثاغورس می توان ضلع سوم را بدست آورد.
رابطه فیثاغورس: \({a^2} = {b^2} + {c^2}\)
در هر مثلث، مربع اندازه هر ضلع برابر است با مجموع مربع های اندازه های دو ضلع دیگر منهای دو برابر حاصل ضرب آنها در کسینوس زاویه بین آنها.
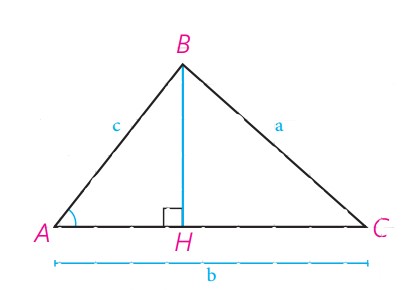
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc{\mathop{\rm Cos}\nolimits} A\\\\{b^2} = {a^2} + {c^2} - 2ac{\mathop{\rm Cos}\nolimits} B\\\\{c^2} = {a^2} + {b^2} - 2ab{\mathop{\rm Cos}\nolimits} C\end{array}\)
اثبات
رابطه اول را ثابت می کنیم دو رابطه دیگر به طور مشابه اثبات می شوند.
حالت اول در مثلث ABC زاویه \(\hat A < {90^0}\)
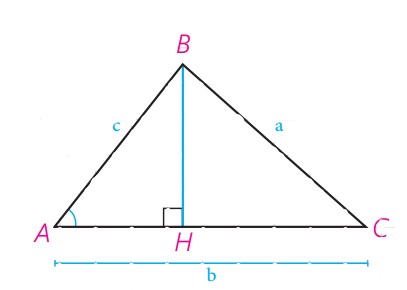
\(\begin{array}{l}\mathop {ABH}\limits^\Delta :{\mathop{\rm Cos}\nolimits} A = \frac{{AH}}{c} \Rightarrow AH = c \times {\mathop{\rm Cos}\nolimits} A\\\\CH = b - AH \Rightarrow CH = b - c{\mathop{\rm Cos}\nolimits} A\\\\{\mathop{\rm Sin}\nolimits} A = \frac{{BH}}{c} \Rightarrow BH = c \times {\mathop{\rm Sin}\nolimits} A\\\\{a^2} = B{H^2} + C{H^2}\\\\ \Rightarrow {a^2} = {\left( {c \times {\mathop{\rm Sin}\nolimits} A} \right)^2} + {\left( {b - c{\mathop{\rm Cos}\nolimits} A} \right)^2}\\\\{a^2} = {c^2}{{\mathop{\rm Sin}\nolimits} ^2}A + {b^2} - 2bc{\mathop{\rm Cos}\nolimits} A + {c^2}{{\mathop{\rm Cos}\nolimits} ^2}A\\\\{a^2} = {c^2}\left( {{{{\mathop{\rm Sin}\nolimits} }^2}A + {{{\mathop{\rm Cos}\nolimits} }^2}A} \right) + {b^2} - 2bc{\mathop{\rm Cos}\nolimits} A\\\\{a^2} = {c^2} + {b^2} - 2bc{\mathop{\rm Cos}\nolimits} A\end{array}\)
حالت دوم در مثلث ABC زاویه \(A > {90^0}\) باشد.
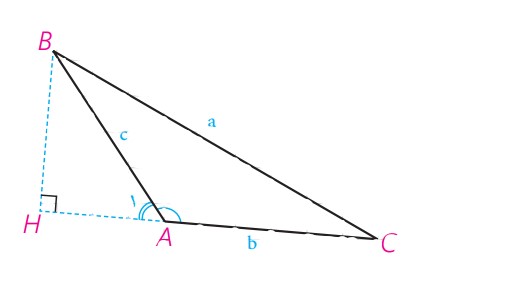
\(\begin{array}{l}{A_1} = 180 - A\\\\ \Rightarrow {\mathop{\rm Sin}\nolimits} {A_1} = {\mathop{\rm Sin}\nolimits} \left( {180 - A} \right) = {\mathop{\rm Sin}\nolimits} A\\\\ \Rightarrow {\mathop{\rm Cos}\nolimits} {A_1} = {\mathop{\rm Cos}\nolimits} \left( {180 - A} \right) = - {\mathop{\rm Cos}\nolimits} A\\\\{\mathop{\rm Cos}\nolimits} {A_1} = \frac{{AH}}{C} \Rightarrow AH = c \times {\mathop{\rm Cos}\nolimits} {A_1}\\\\ \Rightarrow AH = - c \times {\mathop{\rm Cos}\nolimits} A\\\\ \Rightarrow CH = b - c{\mathop{\rm Cos}\nolimits} A\\\\ \Rightarrow BH = c \times {\mathop{\rm Sin}\nolimits} A\\\\B{C^2} = B{H^2} + C{H^2}\\\\{a^2} = {\left( {C{\mathop{\rm Sin}\nolimits} A} \right)^2} + {\left( {b - c{\mathop{\rm Cos}\nolimits} A} \right)^2}\\\\{a^2} = {c^2}{{\mathop{\rm Sin}\nolimits} ^2}A + {b^2} - 2bc{\mathop{\rm Cos}\nolimits} A + {c^2}{{\mathop{\rm Cos}\nolimits} ^2}A\\\\{a^2} = {c^2}\left( {{{{\mathop{\rm Sin}\nolimits} }^2}A + {{{\mathop{\rm Cos}\nolimits} }^2}A} \right) + {b^2} - 2bc{\mathop{\rm Cos}\nolimits} A\\\\ \Rightarrow {a^2} = {c^2} + {b^2} - 2bc{\mathop{\rm Cos}\nolimits} A\end{array}\)
دو قایق از یک نقطه در دریاچه ای با سرعت های \(60km/h\) و \(100km/h\) و با زاویه \({120^0}\) از هم دور می شوند. نیم ساعت بعد دو قایق در چه فاصله ای از یکدیگر هستند؟
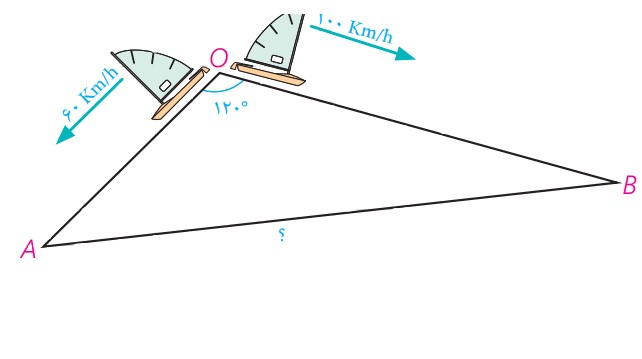
با توجه به نقطه شروع دو قایق و سرعت های ثابت، نیم ساعت بعد، مسافت طی شده توسط هر قایق محاسبه می شود:
\(\begin{array}{l}OA = 60 \times 0/5 = 30\;,\;OB = 100 \times 0/5 = 50\\\end{array}\)
حال به کمک قضیه کسینوس ها می نویسیم:
\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} - 2OA \times {\mathop{\rm Cos}\nolimits} {120^0}\\\\A{B^2} = 900 + 2500 - 2 \times 30 \times 50\left( { - \frac{1}{2}} \right)\\\\A{B^2} = 4900 \Rightarrow AB = 70km\end{array}\)
تهیه کننده: امیرحسین مطلبی
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
قضیه میانه ها
فصل 3 : روابط طولی در مثلث
قضیه میانه ها
در مثلث ABC میانه AM را رسم کرده ایم، ثابت کنید:
\({b^2} + {c^2} = 2A{M^2} + \frac{{{a^2}}}{2}\)
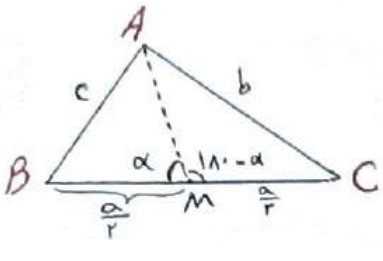
با استفاده از قضیه کسینوس ها در دو مثلث \(\mathop {ABM}\limits^\Delta \) و \(\mathop {ACM}\limits^\Delta \) داریم:
\(\begin{array}{l}\mathop {ABM}\limits^\Delta :A{B^2} = A{M^2} + B{M^2} - 2AM.BM{\mathop{\rm Cos}\nolimits} \alpha \\\\ \Rightarrow {c^2} = A{M^2} + {\left( {\frac{a}{2}} \right)^2} - 2AM.\left( {\frac{a}{2}} \right){\mathop{\rm Cos}\nolimits} \alpha \\\\\mathop {ACM}\limits^\Delta :A{C^2} = A{M^2} + C{M^2} - 2AM.CM - {\mathop{\rm Cos}\nolimits} \alpha \\\\ \Rightarrow {b^2} = A{M^2} + {\left( {\frac{a}{2}} \right)^2} + 2AM.\left( {\frac{a}{2}} \right){\mathop{\rm Cos}\nolimits} \alpha \\\\{c^2} + {b^2} = 2A{M^2} + \frac{{{a^2}}}{2}\end{array}\)
رابطه بالا برای میانه های دیگر مثلث نیز برقرار است:
\(\begin{array}{l}{a^2} + {c^2} = 2B{M^2} + \frac{{{b^2}}}{2}\\\\{a^2} + {b^2} = 2C{M^2} + \frac{{{c^2}}}{2}\end{array}\)
در مثلث ABC اگر \(AB = 4\) ، \(AC = 6\) و \(BC = 8\) باشد طول میانه AM را بدست آورید.
\(\begin{array}{l}{b^2} + {c^2} = 2A{M^2} + \frac{{{a^2}}}{2}\\\\{6^2} + {4^2} = 2A{M^2} + \frac{{{8^2}}}{2}\\\\64 + 16 = 2A{M^2} + 32\\\\A{M^2} = 8 \Rightarrow AM = \sqrt 8 \end{array}\)
تهیه کننده: امیرحسین مطلبی
قضیه نیم ساز های زوایای داخلی
فصل 3 : روابط طولی در مثلث
قضیه نیم ساز های زوایای داخلی
در هر مثلث نیم ساز زاویه داخلی، ضلع رو به رو به آن زاویه را به نسبت اندازه های دو ضلع دیگر مثلث تقسیم می کند.
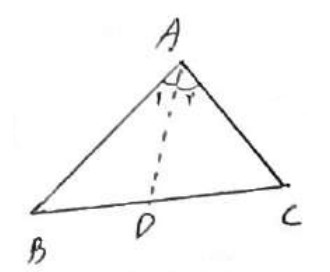
فرض: \({\hat A_1} = {\hat A_2}\)
حکم: \(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}}\)
اثبات
از نقطه C خطی موازی با نیم ساز AD رسم می کنیم تا امتداد AB را در E قطع کند.
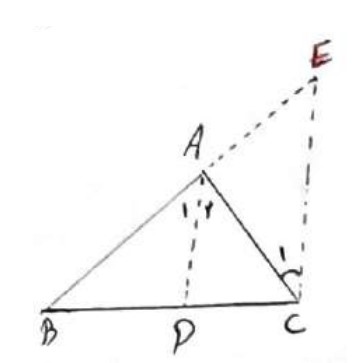
\(\begin{array}{l}AD\parallel EC \Rightarrow {{\hat A}_2} = {{\hat C}_1}\\\\AD\parallel EC \Rightarrow {{\hat A}_1} = \hat E\\\\ \Rightarrow {{\hat A}_1} = {{\hat A}_2} \Rightarrow {{\hat C}_1} = \hat E\\\\ \Rightarrow A\mathop E\limits^\Delta C \Rightarrow AE = AC\\\\\mathop {BEC}\limits^\Delta :AD\parallel EC \Rightarrow \frac{{BD}}{{DC}} = \frac{{AB}}{{AE}}\\\\ \Rightarrow AE = AC \Rightarrow \frac{{BD}}{{DC}} = \frac{{AB}}{{AC}}\end{array}\)
اندازه سه ضلع مثلث 8، 12 و 15 سانتی متر می باشند، اندازه پاره خط هایی که نیم ساز درونی زاویه بزرگتر مثلث بر ضلع مقابل آن پدید می آورد را تعیین کنید.
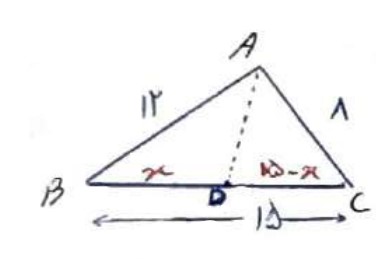
\(\begin{array}{l}\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} = \frac{{12}}{8}\\\\\frac{x}{{15 - x}} = \frac{3}{2} \Rightarrow 2x = 45 - 3x\\\\ \Rightarrow 5x = 45 \Rightarrow x = 9\\\\ \Rightarrow BD = 9\;,\;CD = 6\end{array}\)
تهیه کننده: امیرحسین مطلبی
قضیه محاسبه طول نیم ساز ها
فصل 3 : روابط طولی در مثلث
قضیه محاسبه طول نیم ساز ها
در هر مثلث، مربع اندازه هر نیم ساز داخلی برابر است با حاصل ضرب اندازه دو ضلع زاویه، منهای حاصل ضرب اندازه ی دو قطعه ای که نیم ساز روی ضلع مقابل ایجاد می کند.
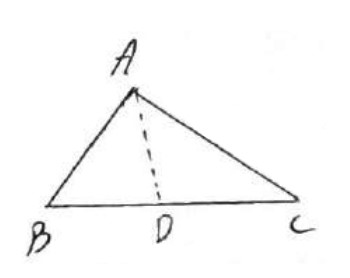
حکم: \(A{D^2} = AB \times AC - BD \times DC\)
اثبات
ابتدا دایره محیطی مثلث ABC را رسم می کنیم و نیم ساز AD را امتداد می دهیم تا دایره محیطی را در نقطه E قطع کند.
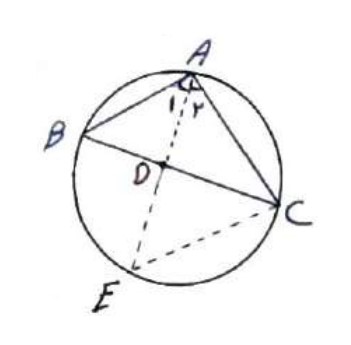
\(\begin{array}{l}AD \Rightarrow {{\hat A}_1} = {{\hat A}_2}\\\\\hat B = \hat E = \frac{{AC}}{2}\\\\\mathop {ABD}\limits^\Delta \sim \mathop {AEC}\limits^\Delta \Rightarrow \frac{{AC}}{{AD}} = \frac{{AE}}{{AB}} = \frac{{CE}}{{BD}}\\\\ \Rightarrow \frac{{AC}}{{AD}} = \frac{{AE}}{{AB}} \Rightarrow AB \times AC = AD \times AE\\\\ \Rightarrow AE = AD + DE\\\\ \Rightarrow AB \times AC = AD\left( {AD + DE} \right)\\\\ \Rightarrow AB \times AC = A{D^2}AD \times AE\\\\ \Rightarrow AD \times AE = BD \times DC\\\\ \Rightarrow AB \times AC = A{D^2}BD \times DC\\\\ \Rightarrow A{D^2} = AB \times AC - BD \times DC\end{array}\)
در مثلث ABC، \(AB = 7\) ، \(AC = 5\) و \(BC = 10\) است؛ طول نیم ساز زاویه داخلی C را بدست آورید.
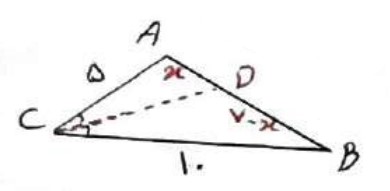
\(\begin{array}{l}\frac{{CA}}{{CB}} = \frac{{AD}}{{BD}} \Rightarrow \frac{5}{{10}} = \frac{{AD}}{{BD}} \Rightarrow \frac{1}{2} = \frac{x}{{7 - x}}\\\\ \Rightarrow 2x = 7 - x \Rightarrow x = \frac{7}{3} \Rightarrow AD = \frac{7}{3}\\\\BD = 7 - \frac{7}{3} = \frac{{14}}{3}\\\\C{D^2} = CA \times CB - AD \times BD\\\\ \Rightarrow C{D^2} = 5 \times 10 - \frac{7}{3} \times \frac{{14}}{3} = 50 - \frac{{98}}{9} = \frac{{352}}{9}\\\\ \Rightarrow CD = \frac{{\sqrt {352} }}{3}\end{array}\)
تهیه کننده: امیرحسین مطلبی
- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
قضیه هرون
فصل 3 : روابط طولی در مثلث
قضیه هرون
مساحت مثلث ABC با طول اضلاع a، b و c از رابطه زیر حاصل می شود:
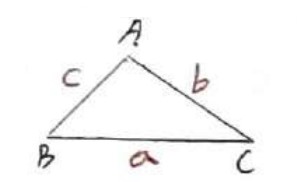
\(S = \sqrt {P\left( {P - a} \right)\left( {P - b} \right)\left( {P - c} \right)} \)
P نصف محیط است یعنی:
\(P = \frac{{a + b + c}}{2}\)
مثال
مساحت مثلثی با اضلاع 4، 5 و 7 را با استفاده از دستور هرون محاسبه کنید.
\(\begin{array}{l}P = \frac{{7 + 5 + 4}}{2} = \frac{{16}}{2} = 8\\\\S = \sqrt {P\left( {P - a} \right)\left( {P - b} \right)\left( {P - c} \right)} \\\\S = \sqrt {8\left( {8 - 4} \right)\left( {8 - 5} \right)\left( {8 - 7} \right)} \\\\S = \sqrt {8 \times 4 \times 3 \times 1} \Rightarrow S = 4\sqrt 6 \end{array}\)
قضیه
مساحت هر مثلث برابر است با نصف حاصل ضرب اندازه دو ضلع در سینوس زاویه بین آنها.
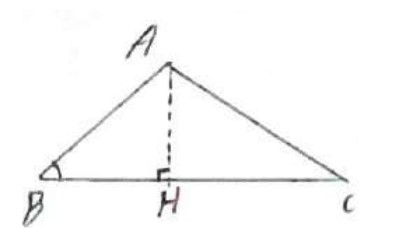
حکم: \({S_{A\mathop B\limits^\Delta C}} = \frac{1}{2}AB \times BC \times {\mathop{\rm Sin}\nolimits} B\)
اثبات
\(\begin{array}{l}{\mathop{\rm Sin}\nolimits} B = \frac{{AH}}{{AB}} \Rightarrow AH = AB \times {\mathop{\rm Sin}\nolimits} \hat B\\\\{S_{A\mathop B\limits^\Delta C}} = \frac{1}{2}AH \times BC\\\\ \Rightarrow {S_{A\mathop B\limits^\Delta C}} = \frac{1}{2}AB \times BC \times {\mathop{\rm Sin}\nolimits} B\end{array}\)
به طور مشابه اثبات می شود:
\(\begin{array}{l}S = \frac{1}{2}ab{\mathop{\rm Sin}\nolimits} C\\\\S = \frac{1}{2}bc{\mathop{\rm Sin}\nolimits} A\end{array}\)
1 چهار ضلعی ABCD که در آن \(\hat A = {90^0}\) است یک زمین کشاورزی را نشان می دهد مساحت این زمین را بدست آورید.
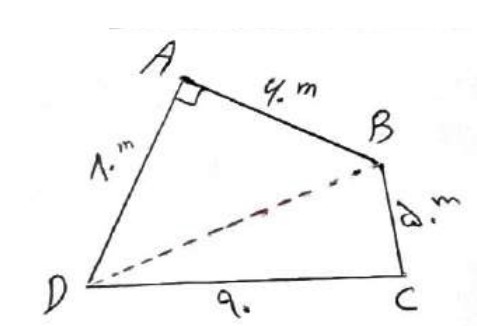
\(\begin{array}{l}B{D^2} = {80^2} + {60^2} \Rightarrow BD = \sqrt {10000} = 100\\\\{P_{B\mathop C\limits^\Delta D}} = \frac{{50 + 90 + 100}}{2} = 120\\\\{S_{A\mathop B\limits^\Delta D}} = \frac{1}{2} \times 60 \times 80 = 2400\\\\{S_{B\mathop C\limits^\Delta D}} = \sqrt {P\left( {P - a} \right)\left( {P - b} \right)\left( {P - c} \right)} \\\\ \Rightarrow \sqrt {120\left( {120 - 50} \right)\left( {120 - 90} \right)\left( {120 - 100} \right)} \\\\ \Rightarrow \sqrt {120 \times 20 \times 30 \times 70} = 600\sqrt {14} \\\\{S_T} = 2400 + 600\sqrt {14} \simeq 4650{m^2}\end{array}\)
2 مساحت مثلث زیر را بدست آورید.
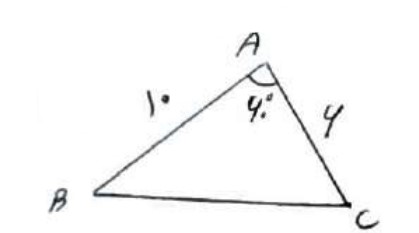
\(\begin{array}{l}{S_{A\mathop B\limits^\Delta C}} = \frac{1}{2} \times 6 \times 10 \times {\mathop{\rm Sin}\nolimits} {60^0}\\\\{S_{A\mathop B\limits^\Delta C}} = 3 \times 10 \times \frac{{\sqrt 3 }}{2} = 15\sqrt 3 \end{array}\)
تهیه کننده: امیرحسین مطلبی



1736019749.png)