جواب تمرین های ترکیبی صفحه 18 درس 1 ریاضی هشتم (عددهای صحیح و گویا)
تعداد بازدید : 84.72Mپاسخ تمرین های ترکیبی صفحه 18 ریاضی هشتم
-گام به گام تمرین های ترکیبی صفحه 18 درس عددهای صحیح و گویا
-تمرین های ترکیبی صفحه 18 درس 1
-شما در حال مشاهده جواب تمرین های ترکیبی صفحه 18 ریاضی هشتم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
مفاهیم و مهارت ها
در این فصل اصطلاحات زیر به کار رفته اند. مطمئن شوید که می توانید با جمله های خود، آنها را تعریف کنید و برای هر کدام مثالی بزنید.
1 عددهای طبیعی
2 عددهای صحیح
3 عددهای گویا
4 معکوس عدد گویا
1 عددهای طبیعی
عددهای طبیعی اولین عددهایی هستند که برای شمارش اشیاء در طبیعت به کار میبریم. آنها از ۱ شروع میشوند و تا بینهایت ادامه دارند.
مثال: ۱، ۲، ۳، ۱۰۰، ۴۵۰
نکته کلیدی: به یاد داشته باش که صفر جزو عددهای طبیعی نیست. این عددها پایهایترین بلوکهای سازنده دنیای ریاضیات هستند.
2 عددهای صحیح
دنیای عددهای صحیح، بزرگتر و کاملتر از عددهای طبیعی است. این مجموعه شامل تمام عددهای طبیعی، صفر و قرینهٔ عددهای طبیعی (یعنی عددهای منفی) میشود.
مثال: … , -3 , -2 , -1 , 0 , 1 , 2 , 3 , …
نکته کلیدی: فکر کن یک محور اعداد داری که از صفر شروع شده و هم به سمت راست (مثبت) و هم به سمت چپ (منفی) تا بینهایت ادامه دارد. عددهای صحیح، تمام ایستگاههای اصلی و کامل روی این محور هستند.
3 عددهای گویا
هر عددی که بتوانی آن را به صورت یک \(\frac{a}{b}\) بنویسی، به طوری که صورت (a) و مخرج (b) آن عددهای صحیح باشند و مخرج (b) صفر نباشد، یک عدد گویا است.
مثال: \( - 5\,,\,\frac{2}{3}\) (چون میتوان آن را به صورت \(\frac{{ - 5}}{1}\) نوشت)، 0/25 (چون برابر با \(\frac{1}{4}\) است) و حتی تمام عددهای صحیح و طبیعی، همگی گویا هستند.
نکته کلیدی: کلمه «گویا» به معنی «نسبتپذیر» است. یعنی این عددها نسبت بین دو عدد صحیح را بیان میکنند. این مجموعه اعداد، بیشتر عددهایی را که روزمره با آنها سروکار داریم، در بر میگیرد.
4 معکوس عدد گویا
معکوس یک عدد گویای غیرصفر، عددی است که اگر در عدد اصلی ضرب شود، حاصل آن همیشه برابر با ۱ میشود. برای پیدا کردن معکوس یک کسر، کافی است جای صورت و مخرج آن را عوض کنی.
مثال: معکوس کسر \(\frac{2}{3}\) برابر با \(\frac{3}{2}\) است. معکوس عدد 7- (که همان \(\frac{{ - 7}}{1}\) است) برابر با \( - \frac{1}{7}\) می شود.
نکته کلیدی: حواست باشد که علامت عدد در معکوس تغییر نمیکند و مهمتر از آن، عدد صفر تنها عددی است که معکوس ندارد، زیرا کسری که مخرج آن صفر باشد در ریاضیات تعریف نشده است.
در این فصل، روش های اصلی زیر معرفی شده اند. هر کدام را با یک مثال توضیح دهید و در دفتر خود، خلاصهٔ درس مربوط به آن را بنویسید.
1 محاسبهٔ حاصل یک عبارت، شامل عددهای صحیح با رعایت ترتیب عملیات
2 پیدا کردن راه حل مناسب برای محاسبهٔ یک عبارت
3 پیدا کردن عددهای گویای مساوی
4 نمایش جمع و تفریق عدد های گویا روی محور
5 محاسبهٔ جمع و تفریق دو عدد گویا
6 محاسبهٔ ضرب و تقسیم دو عدد گویا
7 پیدا کردن معکوس یک عدد گویا
8 محاسبهٔ حاصل یک عبارت، شامل عددهای گویا با رعایت ترتیب عملیات
۱ محاسبهی حاصل یک عبارت، شامل عددهای صحیح با رعایت ترتیب عملیات
اصل کلیدی: در ریاضیات، برای جلوگیری از سردرگمی، یک ترتیب استاندارد برای انجام عملیات وجود دارد. این اولویتبندی را به خاطر بسپار:
پرانتزها: همیشه اول از همه به سراغ داخلیترین پرانتزها برو.
ضرب و تقسیم: پس از پرانتزها، هر ضرب یا تقسیمی که وجود دارد را از چپ به راست انجام بده.
جمع و تفریق: در نهایت، جمع و تفریقها را از چپ به راست محاسبه کن.
یک مثال کاربردی:
در عبارت -8-2×5= ، اولویت با ضرب است.
-8-2×5=-8-10=-18
نکته مربی: همیشه قبل از شروع محاسبه، یک نگاه کلی به عبارت بینداز و نقشه راهت را مشخص کن: اول پرانتزها، بعد ضرب و تقسیم، و در آخر جمع و تفریق.
۲ پیدا کردن راه حل مناسب برای محاسبهی یک عبارت
اصل کلیدی: گاهی اوقات، هوشمندانه عمل کردن بهتر از سختکوشی است! قبل از شروع محاسبه، به دنبال راههایی برای سادهسازی بگرد. مثلاً عددهایی را پیدا کن که یکدیگر را خنثی میکنند یا حاصلشان یک عدد رُند میشود.
یک مثال کاربردی:
در عبارت 40+17+80-35-40 به جای محاسبه از چپ به راست، عددهای مناسب را کنار هم بگذار.
(40-40)+(35-80+17)=0-45+17=-28
نکته مربی: مثل یک کارآگاه به دنبال سرنخ باش! عددهای قرینه، یا عددهایی که با هم یک عدد رند (مثل ۱۰ یا ۱۰۰) میسازند، بهترین دوستان تو در سادهسازی عبارتها هستند.
۳ پیدا کردن عددهای گویای مساوی
اصل کلیدی: ارزش یک کسر تغییر نمیکند اگر صورت و مخرج آن را در یک عدد غیرصفر ضرب یا بر آن تقسیم کنیم. این کار مانند تغییر تعداد برشهای پیتزا است؛ اندازه برشها تغییر میکند، اما مقدار کل پیتزا ثابت است.
یک مثال کاربردی:
همانطور که در شکلهای کتاب دیدی، کسرهای \(\frac{{ - 4}}{6}\,\,,\,\,\frac{{ - 2}}{3}\) و \(\frac{{ - 6}}{9}\) همگی یک مقدار را روی محور نشان میدهند.
\(\frac{{ - 2}}{3} = - \frac{{2 \times 2}}{{3 \times 2}} = \frac{{ - 4}}{6}\)
نکته مربی: این مهارت، شاهکلید جمع و تفریق کسرهاست! برای اینکه بتوانی کسرها را با هم جمع یا تفریق کنی، اول باید با استفاده از این روش، آنها را هممخرج کنی.
۴ نمایش جمع و تفریق عددهای گویا روی محور
اصل کلیدی: هر عدد گویا یک حرکت روی محور است. عدد مثبت حرکت به راست و عدد منفی حرکت به چپ را نشان میدهد. برای جمع کردن، حرکت دوم را از انتهای حرکت اول شروع میکنیم.
یک مثال کاربردی:
برای نمایش \(( + \frac{3}{4}) + ( - \frac{6}{4})\)، ابتدا از صفر به اندازه \(\frac{3}{4}\) به راست میرویم و سپس از همان نقطه، به اندازه \(\frac{6}{4}\) به چپ برمیگردیم.
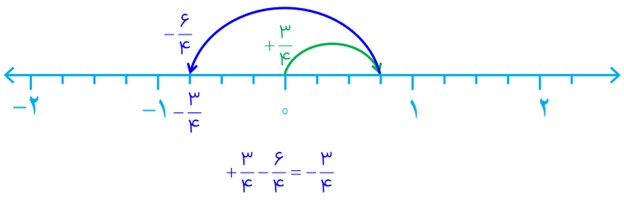
نکته مربی: محور اعداد، داستان تصویری یک عبارت ریاضی است. از این ابزار قدرتمند برای درک بهتر جمع و تفریق، به خصوص وقتی با عددهای منفی سروکار داری، استفاده کن.
۵ محاسبهی جمع و تفریق دو عدد گویا
اصل کلیدی: برای جمع یا تفریق کسرها، ابتدا باید آنها را هممخرج کنی. پس از پیدا کردن مخرج مشترک، فقط صورتها را با هم جمع یا تفریق میکنی و مخرج را ثابت نگه میداری.
یک مثال کاربردی:
برای محاسبه \(\frac{5}{6} - \frac{3}{4}\)، کوچکترین مخرج مشترک بین ۶ و ۴، عدد ۱۲ است.
\(\frac{5}{6} - \frac{3}{4} = \frac{{5 \times 2}}{{6 \times 2}} - \frac{{3 \times 3}}{{4 \times 3}} = \frac{{10}}{{12}} - \frac{9}{{12}} = \frac{{10 - 9}}{{12}}\, = \frac{1}{{12}}\)
نکته مربی: قبل از هر کاری، روی پیدا کردن کوچکترین مخرج مشترک (ک.م.م) تمرکز کن. این کار محاسبات تو را در ادامه مسیر بسیار سادهتر میکند.
۶ محاسبهی ضرب و تقسیم دو عدد گویا
اصل کلیدی:
ضرب: کار بسیار ساده است؛ صورتها در هم و مخرجها در هم ضرب میشوند.
تقسیم: تقسیم، در واقع یک ضرب پنهان است! برای تقسیم دو کسر، کسر اول را در معکوس کسر دوم ضرب کن.
یک مثال کاربردی:
ضرب:
\( - \frac{3}{4} \times ( - \frac{8}{{15}}) = + \frac{{3 \times 8}}{{4 \times 15}} = + \frac{{24}}{{60}} = \frac{2}{5}\)
تقسیم:
\(\begin{array}{l}( - \frac{7}{9}) \div ( - \frac{{28}}{{27}}) = ( - \frac{7}{9}) \times ( - \frac{{27}}{{28}}) = \\\\ + \frac{{7 \times 27}}{{9 \times 28}} = \frac{3}{4}\end{array}\)
نکته مربی: یک استراتژی هوشمندانه: قبل از ضرب کردن، تا جایی که ممکن است صورت را با مخرج ساده کن. این کار از بزرگ شدن بیدلیل عددها جلوگیری میکند.
۷ پیدا کردن معکوس یک عدد گویا
اصل کلیدی: معکوس یک عدد گویای غیرصفر، عددی است که اگر در آن ضرب شود، حاصل برابر با ۱ میشود. برای پیدا کردنش، فقط کافی است جای صورت و مخرج کسر را عوض کنی.
یک مثال کاربردی:
معکوس \( - \frac{3}{5}\) برابر است با \( - \frac{5}{3}\).
معکوس عدد 4- (که همان \(\frac{{ - 4}}{1}\) است) برابر است با \(\frac{1}{{ - 4}}\) یا \( - \frac{1}{4}\).
نکته مربی: یادت باشد، علامت عدد در معکوس تغییری نمیکند و تنها عددی که معکوس ندارد، صفر است.
۸ محاسبهی حاصل یک عبارت، شامل عددهای گویا با رعایت ترتیب عملیات
اصل کلیدی: قوانینی که برای ترتیب عملیات عددهای صحیح یاد گرفتی، دقیقاً برای عددهای گویا (کسرها، اعشار و اعداد مخلوط) هم کاربرد دارد. همان نقشه راه همیشگی است: اول پرانتز، بعد ضرب و تقسیم، و در آخر جمع و تفریق.
یک مثال کاربردی:
در عبارت \( - 1\frac{2}{3} - 1\frac{1}{4} \times \frac{{ - 8}}{5}\)، اولویت با ضرب است.
الف ضرب:
\(1\frac{1}{4} \times \frac{{ - 8}}{5} = \frac{5}{4} \times \frac{{ - 8}}{5} = \frac{{ - 8}}{4} = - 2\)
ب تفریق:
\( - 1\frac{2}{3} - ( - 2) = - \frac{5}{3} + 2 = \frac{{ - 5 + 6}}{3} = \frac{1}{3}\)
نکته مربی: با عبارات طولانی، آرامش خودت را حفظ کن. مرحله به مرحله و با دقت پیش برو. هر بار فقط یک عملیات را طبق اولویت انجام بده تا به جواب برسی. تو میتوانی!
تمرین های ترکیبی
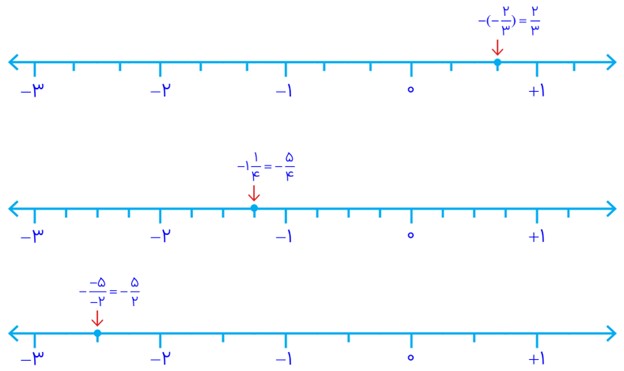
1 عدد های گویا را روی محور نمایش دهید.
\(\begin{array}{l} - ( - \frac{2}{3})\\\\ - 1\frac{1}{4}\\\\ - \frac{{ - 5}}{{ - 2}}\end{array}\)
\(\begin{array}{l} - ( - \frac{2}{3}) = \frac{2}{3}\\\\ - 1\frac{1}{4} = - \frac{5}{4}\\\\ - \frac{{ - 5}}{{ - 2}} = - \frac{5}{2}\end{array}\)
2 حاصل عبارت های زیر را به دست آورید.
\(\begin{array}{l}( - 2\frac{1}{2} + 1\frac{1}{3}) \div ( - 1\frac{1}{4} \times \frac{{ - 2}}{5}) = \\\\1 - \frac{{1 - 1\frac{1}{2}}}{{ - 1 + 1\frac{1}{2}}} = \end{array}\)
\(\begin{array}{l}( - 2\frac{1}{2} + 1\frac{1}{3}) \div ( - 1\frac{1}{4} \times \frac{{ - 2}}{5}) = \\\\( - \frac{5}{2} + \frac{4}{3}) \div ( - \frac{5}{4} \times \frac{{ - 2}}{5}) = \\\\(\frac{{ - 15 + 8}}{6}) \div (\frac{{10}}{{20}}) = \\\\( - \frac{7}{6}) \div (\frac{1}{2}) = - \frac{7}{6} \times \frac{2}{1} = \\\\ - \frac{{14}}{6} = - \frac{7}{3}\end{array}\)
\(\begin{array}{l}1 - \frac{{1 - 1\frac{1}{2}}}{{ - 1 + 1\frac{1}{2}}} = 1 - \frac{{1 - \frac{3}{2}}}{{ - 1 + \frac{3}{2}}} = \\\\1 - \frac{{\frac{{2 - 3}}{2}}}{{\frac{{ - 2 + 3}}{2}}} = 1 - \frac{{ - \frac{1}{2}}}{{\frac{1}{2}}} = \\\\1 - ( - 1) = 1 + 1 = 2\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















