جواب تمرین صفحه 63 درس 3 هندسه دهم (چند ضلعی ها)

\(\begin{array}{l}\frac{{n\left( {n - 2} \right)}}{3} = n\\\\ \Rightarrow {n^2} - 2n = 3n\\\\ \Rightarrow {n^2} = 5n\\\\ \Rightarrow n = 5\end{array}\)

قطرهای \(BD\) و \(B’D’\) را در دو چهار ضلعی رسم می کنیم. بدیهی است که دو مثلث \(BCD\) و \(B’C’D’\) همنهشت اند (ض ز ض). بنابراین :

\(\widehat {{B_1}} = \widehat {{{B'}_1}}\;\;\mathop  \Rightarrow \limits^{\widehat B = \widehat {B'}} \;\;\widehat {{B_2}} = \widehat {{{B'}_2}}\)

در دو مثلث ABD و A’B’D’ :

\(\begin{array}{l}\left. \begin{array}{l}AB = A'B'\\\widehat {{B_2}} = \widehat {{{B'}_2}}\\BD = B'D'\end{array} \right\} \Rightarrow A\mathop B\limits^\Delta  D \cong A'\mathop {B'}\limits^\Delta  D'\\\\\mathop  \Rightarrow \limits^{B\mathop C\limits^\Delta  D \cong B'\mathop {C'}\limits^\Delta  D'} \;A\mathop {BC}\limits^{} D \cong A'\mathop {B'C'}\limits^{} D'\end{array}\)

 قطرهای AC و A’C’ را در دو چهار ضلعی  رسم می کنیم. بدیهی است که دو مثلث ABC و A’B’C’ همنهشت اند . بنابراین :

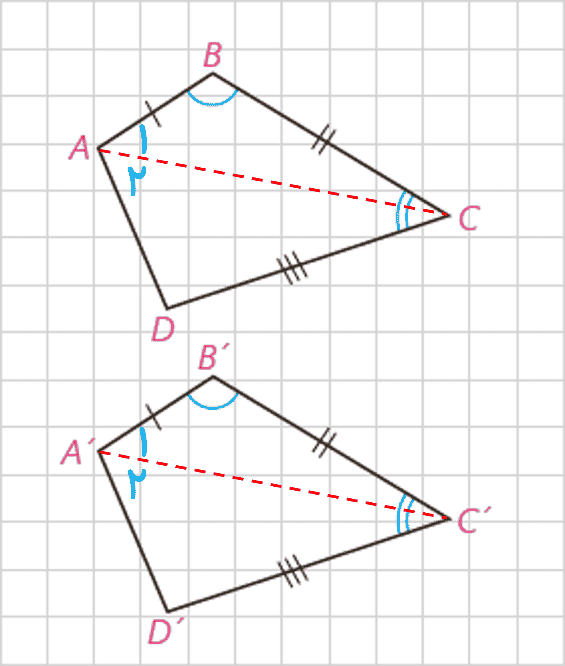
\(\widehat {{A_1}} = \widehat {{{A'}_1}}\;\;\mathop  \Rightarrow \limits^{\widehat A = \widehat {A'}} \;\;\widehat {{A_2}} = \widehat {{{A'}_2}}\)

در دو مثلث ADC و A’D’C’ :

\(\begin{array}{l}\left. \begin{array}{l}CD = C'D'\\\widehat {{A_2}} = \widehat {{{A'}_2}}\\AC = A'C'\end{array} \right\} \Rightarrow A\mathop D\limits^\Delta  C \cong A'\mathop {D'}\limits^\Delta  C'\\\\\mathop  \Rightarrow \limits^{A\mathop B\limits^\Delta  C \cong A'\mathop {B'}\limits^\Delta  C'} \;A\mathop {BC}\limits^{} D \cong A'\mathop {B'C'}\limits^{} D'\end{array}\)

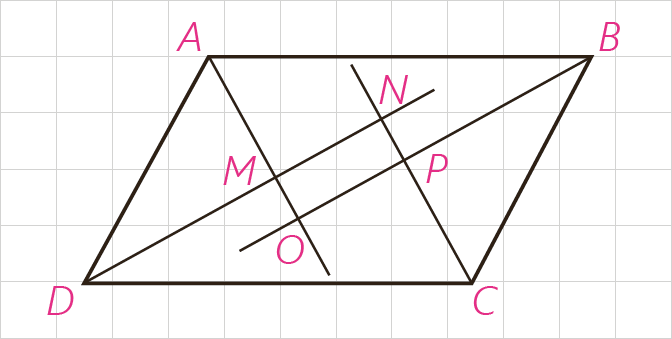
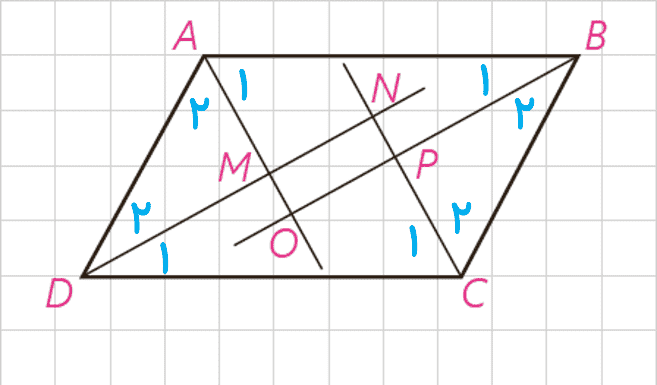
\(\begin{array}{*{20}{l}}\begin{array}{l}A\mathop {BC}\limits^{} D:\;\;\:\hat A + \hat B = {180^\circ }\\\\ \Rightarrow \frac{{\hat A}}{2} + \frac{{\hat B}}{2} = {90^\circ }\\\end{array}\\\begin{array}{l}O\mathop A\limits^\Delta  B:\;\;\:\widehat {{A_1}} + \widehat {{B_1}} = {90^\circ }\\\\ \Rightarrow \hat O = {90^\circ }\;\;\:\left( i \right)\end{array}\end{array}\)

به روش مشابه ثابت می شود که :

\(\begin{array}{*{20}{l}}\begin{array}{l}O\mathop A\limits^\Delta  B:\;\;\:\widehat {{C_1}} + \widehat {{D_1}} = {90^\circ }\\\\ \Rightarrow \hat N = {90^\circ }\;\;\:\left( {ii} \right)\\\end{array}\\\begin{array}{l}P\mathop B\limits^\Delta  C:\;\;\:\widehat {{B_2}} + \widehat {{C_2}} = {90^\circ }\\\\ \Rightarrow \hat P = {90^\circ }\;\;\:\left( {iii} \right)\\\end{array}\\\begin{array}{l}\hat M = {360^\circ } - \left( {\hat O + \hat N + \hat P} \right)\\\\ \Rightarrow \hat M = {90^\circ }\;\;\:\left( {iv} \right)\end{array}\end{array}\)

\(\begin{array}{l}\left( i \right)\:,\:\left( {ii} \right)\:,\:\left( {iii} \right)\:,\:\left( {iv} \right):\\\\\hat M = \hat N = \hat O = \hat P = {90^\circ }\end{array}\)

بنابراین چهار ضلعی MNOP مستطیل است.

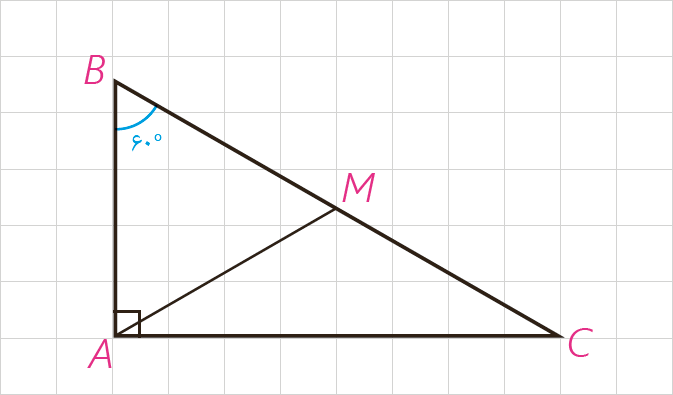
در مثلث قائم الزاویه، میانه وارد بر وتر (\(AM\))، نصف وتر است؛ بنابراین : \(AM = BM = CM = \frac{BC}{2}\).

\(\begin{array}{*{20}{l}}{A\mathop B\limits^\Delta C:\;\;\:\left\{ {\begin{array}{*{20}{l}}{\hat A = {{90}^\circ }}\\{\hat C = {{30}^\circ }}\end{array}} \right. \Rightarrow \hat B = {{60}^\circ }}\\\begin{array}{l}\\A\mathop B\limits^\Delta M:\;\;\:AM = BM \Rightarrow B\hat AM = \hat B = {60^\circ }\\\\ \Rightarrow AM = BM = AB \Rightarrow AB = \frac{{BC}}{2}\end{array}\\\begin{array}{l}\\A\mathop B\limits^\Delta C:\;\;\:\hat A = {90^\circ } \Rightarrow A{B^2} + A{C^2} = B{C^2}\:\:\mathop \Rightarrow \limits^{AB = \frac{{BC}}{2}} \:\:\\\\A{C^2} = B{C^2} - {\left( {\frac{{BC}}{2}} \right)^2} = \frac{{3B{C^2}}}{4} \Rightarrow AC = \frac{{\sqrt 3 }}{2}BC\end{array}\\\begin{array}{l}\\A\mathop B\limits^\Delta C:\;\;\:\left\{ {\begin{array}{*{20}{l}}{\hat A = {{90}^\circ }}\\{\hat B = {{45}^\circ }}\end{array}} \right. \Rightarrow \hat B = \hat C \Rightarrow \left\{ {\begin{array}{*{20}{l}}{AB = AC}\\{A{B^2} + A{C^2} = B{C^2}}\end{array}} \right.\end{array}\\\begin{array}{l}\\ \Rightarrow 2A{B^2} = B{C^2} \Rightarrow A{B^2} = \frac{{B{C^2}}}{2} \Rightarrow AB = \frac{{BC}}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}BC\end{array}\end{array}\)

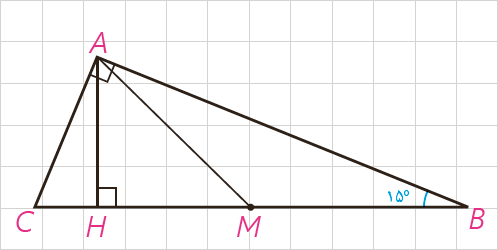
در مثلث قائم الزاویه، میانه وارد بر وتر (\(AM\))، نصف وتر است؛ بنابراین :

\(\begin{array}{l}A\mathop B\limits^\Delta  C:\;\;\:AM = BM = \frac{{BC}}{2}\\\\ \Rightarrow {{\hat A}_1} = \hat B = {15^\circ }\\\\ \Rightarrow {{\hat M}_1} = {{\hat A}_1} + \hat B = {30^\circ }\end{array}\)

از طرف دیگر در مثلث قائم الزاویه ضلع رو به رو به زاویه °30، نصف وتر است :

\(\begin{array}{l}A\mathop M\limits^\Delta  H:\;\;\:\left\{ {\begin{array}{*{20}{l}}{\hat H = {{90}^\circ }}\\{{{\hat M}_1} = {{30}^\circ }}\end{array}} \right. \Rightarrow AH = \frac{{AM}}{2} \Rightarrow \\\\AH = \frac{{\frac{{BC}}{2}}}{2} = \frac{{BC}}{4}\end{array}\)

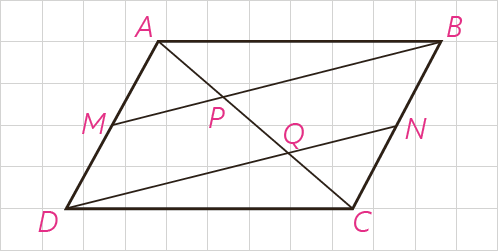
اگر در یک چهار ضلعی، دو ضلع موازی و مساوی باشند، آن چهار ضلعی متوازی الاضلاع است . در چهار ضلعی BMDN داریم :

\(\begin{array}{*{20}{l}}\begin{array}{l}AD = BC\:\:\mathop  \Rightarrow \limits^{ \div 2} \:\:\left\{ {\begin{array}{*{20}{l}}{BN = MD}\\{BN\parallel MD}\end{array}} \right.\\\\ \Rightarrow BM\parallel DN\\\end{array}\\\begin{array}{l}A\mathop D\limits^\Delta  Q:\;\;\:MP\parallel DQ\\\\ \Rightarrow \frac{{AP}}{{PQ}} = \frac{{AM}}{{MQ}} = 1 \Rightarrow AP = PQ\end{array}\\\begin{array}{l}B\mathop C\limits^\Delta  P:\;\;\:BP\parallel QN\\\\ \Rightarrow \frac{{CQ}}{{QP}} = \frac{{CN}}{{NB}} = 1 \Rightarrow CQ = PQ\end{array}\\\begin{array}{l}\\ \Rightarrow AP = PQ = QC\end{array}\end{array}\)

برهان :

فرض کنیم نقاط M ، N ، P و F به ترتیب وسط اضلاع AB ، BC ، CD و AD از چهار ضلعی ABCD باشند. باید ثابت کنیم چهار ضلعی MNEF متوازی الاضلاع است. قطر AC را رسم می کنیم:

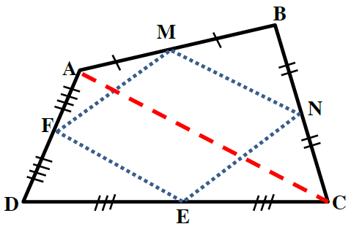
\(\begin{array}{*{20}{l}}\begin{array}{l}A\mathop B\limits^\Delta  C:\;\;\:\frac{{BM}}{{AB}} = \frac{{BN}}{{BC}} = \frac{1}{2}\:\:\\\\ \Rightarrow \:\:\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}MN\parallel AC\\\end{array}\\{MN = \frac{{AC}}{2}}\end{array}} \right.\;\;\:\left( i \right)\\\end{array}\\\begin{array}{l}A\mathop C\limits^\Delta  D:\;\;\:\frac{{DE}}{{DC}} = \frac{{DF}}{{DA}} = \frac{1}{2}\:\:\\\\ \Rightarrow \:\:\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}EF\parallel AC\\\end{array}\\{EF = \frac{{AC}}{2}}\end{array}} \right.\;\;\:\left( {ii} \right)\\\end{array}\\{\mathop  \Rightarrow \limits^{\left( i \right),\left( {ii} \right)} \;\;\:\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}MN\parallel EF\\\end{array}\\{MN = EF}\end{array}} \right.}\end{array}\)

به عبارت دیگر در چهار ضلعی MNEF ، دو ضلع موازی و مساوی اند . لذا چهار ضلعی MNEF متوازی الاضلاع است.

اگر قطرهای چهار ضلعی ABCD بر هم عمود باشند، چهار ضلعی MNEF مستطیل است . زیرا قطرهای چهار ضلعی ABCD با چهار ضلعی MNEF موازی اند .

اگر قطرهای چهار ضلعی ABCD با هم مساوی باشند، چهار ضلعی MNEF لوزی است و اندازه هر ضلع این لوزی، نصف طول قطر چهار ضلعی ABCD است :

\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}MN = EF = \frac{{AC}}{2}\\\end{array}\\{FM = EN = \frac{{BD}}{2}}\end{array}} \right.\\\\ \Rightarrow MN + NE + EF + FM = \\\\2\left( {\frac{{AC}}{2} + \frac{{BD}}{2}} \right) = AC + BD\end{array}\)

محیط چهار ضلعی بوجود آمده MNEF : AC + BD