جواب تمرین صفحه 72 درس 3 هندسه دهم (چند ضلعی ها)
تعداد بازدید : 84.74Mپاسخ تمرین صفحه 72 هندسه دهم
-گام به گام تمرین صفحه 72 درس چند ضلعی ها
-تمرین صفحه 72 درس 3
-شما در حال مشاهده جواب تمرین صفحه 72 هندسه دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 در یک لوزی اندازهٔ هر ضلع \(x = {-b \pm \sqrt{b^2-4ac} \over 2a}2\sqrt {10}\) و نسبت اندازه های دو قطر \(\frac{1}{3}\) است. مساحت لوزی را پیدا کنید.
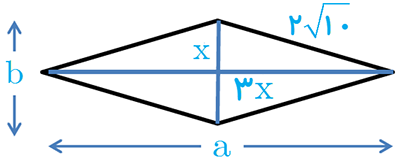
\(\begin{array}{l}{x^2} + {\left( {3x} \right)^2} = {\left( {2\sqrt {10} } \right)^2} \Rightarrow {x^2} + 9{x^2} = 40\\\\ \Rightarrow 10{x^2} = 40 \Rightarrow {x^2} = 4\\\\ \Rightarrow x = 2 \Rightarrow \left\{ \begin{array}{l}a = 6x = 12\\b = 2x = 4\end{array} \right.\\\\ \Rightarrow S = \frac{1}{2} \times a \times b = 24\end{array} \)
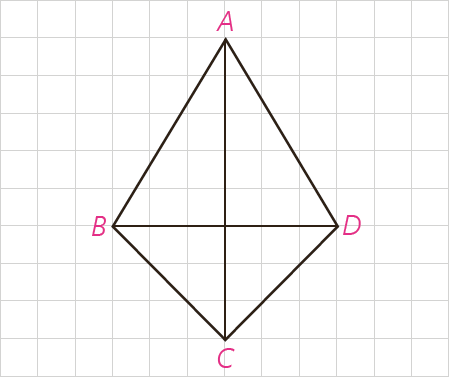
2 در چهارضلعی ABCD، مطابق شکل AB=AD و BC=CD است. آیا قطرهای این چهارضلعی برهم عموداند؟ چرا؟ نشان دهید در این چهارضلعی قطر AC روی نیمسازهای \(\angle A\) و \(\angle C\) است. اگر اندازه های دو قطر ٨ و ٦ باشند، مساحت آن را محاسبه کنید. چهارضلعی ای با این ویژگی کایت نام دارد. نشان دهید در کایت یک قطر عمودمنصف قطر دیگر است.
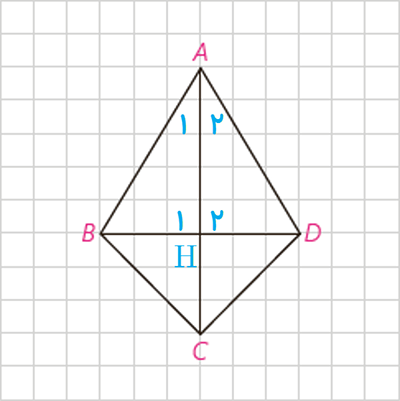
نکته: در فرمول های زیر (commen به معنای مشترک) می باشد.
\(\begin{array}{l}\left. \begin{array}{l}AB = AD\\CB = CD\\AC = common\quad \quad \quad \end{array} \right\} \Rightarrow A\mathop B\limits^\Delta C \cong A\mathop C\limits^\Delta D \Rightarrow \widehat {{A_1}} = \widehat {{A_2}}\\\\\left. \begin{array}{l}AB = AD\\\widehat {{A_1}} = \widehat {{A_2}}\\AH = commen\quad \quad \quad \end{array} \right\} \Rightarrow A\mathop B\limits^\Delta H \cong A\mathop D\limits^\Delta H \Rightarrow \widehat {{H_1}} = \widehat {{H_2}} = {90^ \circ }\\\\AC \bot BD \Rightarrow {S_{A\mathop {BC}\limits^{} D}} = \frac{1}{2}AC \times BD = 24\end{array}\)
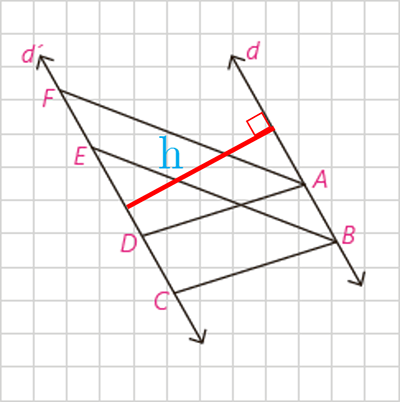
3 در شکل دو خط d و d' موازی اند و ABCD و ABEF هردو متوازی الاضلاع اند. اگر مساحت یکی از این متوازی الاضلاع ها برابر S باشد، مساحت دیگری برحسب S چقدر است؟

فرض می کنیم فاصله دو خط موازی d و d’ باشند. در این صورت داریم :
\({S_{A\mathop {BC}\limits^{} D}} = {S_{A\mathop {BE}\limits^{} F}} = AB \times h\)
4 در ذوزنقهٔ شکل مقابل اندازه های دو قاعده a و b و اندازه های دو زاویهٔ مجاور به یک قاعده °٤٥ است. مساحت ذوزنقه را برحسب a و b محاسبه کنید. از A و B بر قاعده DC عمود کنید.
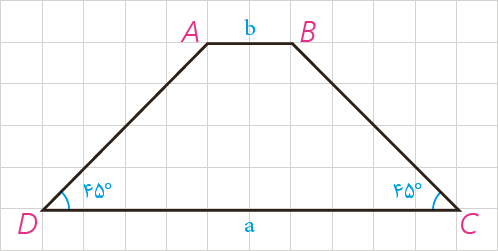
عمودهای AF و BE را بر ضلع DC وارد می کنیم. چهار ضلعی ABEF مستطیل است؛ بنابراین :
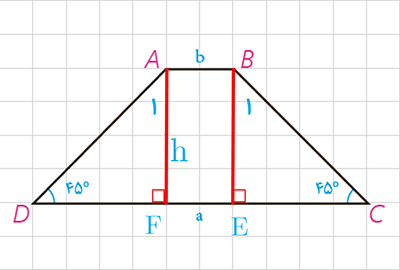
\(\begin{array}{l}AB = EF = b\\\\A\mathop D\limits^\Delta F:\quad \widehat {{A_1}} = \widehat D = {45^ \circ } \Rightarrow AF = DF = h\\\\B\mathop C\limits^\Delta E:\quad \widehat {{B_1}} = \widehat C = {45^ \circ } \Rightarrow BE = CE = h\\\\ \Rightarrow CD = 2h + b = a \Rightarrow h = \frac{{a - b}}{2}\\\\{S_{ABCD}} = \frac{1}{2}\left( {a + b} \right)h\\\\ \Rightarrow {S_{ABCD}} = \frac{{a + b}}{2} \times \frac{{a - b}}{2} = \frac{{{a^2} - {b^2}}}{2}\end{array}\)
5 مساحت ذوزنقهٔ مقابل را به دو طریق به دست آورید. از مساوی قرار دادن آنها چه نتیجه ای به دست می آید؟
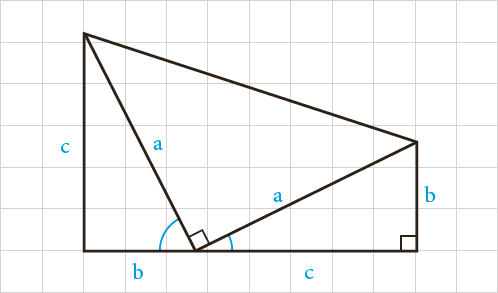
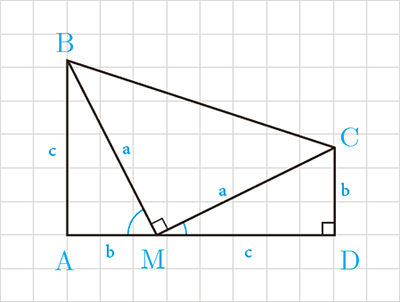
\(\begin{array}{l}{S_{ABCD}} = \frac{1}{2}\left( {AB + CD} \right) \times AD\\ = \frac{1}{2}\left( {b + c} \right)\left( {b + c} \right) = \frac{1}{2}{\left( {b + c} \right)^2}\quad \left( i \right)\\\\{S_{ABCD}} = {S_{A\mathop B\limits^\Delta M}} + {S_{C\mathop D\limits^\Delta M}} + {S_{M\mathop B\limits^\Delta C}}\\ = \frac{1}{2}bc + \frac{1}{2}bc + \frac{1}{2}{a^2} = bc + \frac{1}{2}{a^2}\quad \left( {ii} \right)\\\\\mathop \Rightarrow \limits^{\quad \left( i \right),\left( {ii} \right)} \quad \frac{1}{2}{\left( {b + c} \right)^2} = bc + \frac{1}{2}{a^2}\\ \Rightarrow {\left( {b + c} \right)^2} = 2bc + {a^2}\\\\ \Rightarrow {b^2} + 2bc + {c^2} = 2bc + {a^2}\end{array}\)
\(\Rightarrow {b^2} + {c^2} = {a^2}\) رابطه فیثاغورث :
6 در متوازی الاضلاع ABCD، M وسط ضلع BC است و پاره خط AM قطر BD را در N قطع کرد هاست. نشان دهید:
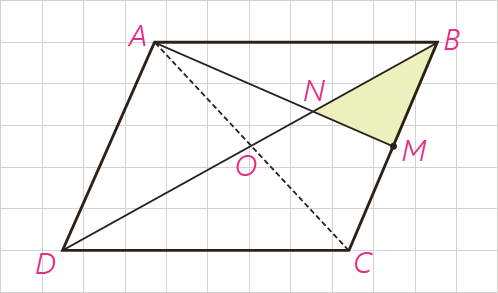
\({S_{BMN}} = \frac{1}{{12}}{S_{ABCD}}\)
\(A\mathop B\limits^\Delta C \cong A\mathop C\limits^\Delta D \Rightarrow {S_{A\mathop B\limits^\Delta C}} = {S_{A\mathop C\limits^\Delta D}} = \frac{1}{2}{S_{A\mathop {BC}\limits^{} D}}\quad \left( i \right)\)
میانه های هر مثلث، آن را به شش قسمت با مساحت های مساوی تقسیم می کند؛ بنابراین :
\(\begin{array}{l}A\mathop B\limits^\Delta C:\quad \left\{ \begin{array}{l}BM = MC\\AO = OC\end{array} \right. \Rightarrow {S_{M\mathop N\limits^\Delta B}} = \frac{1}{6}{S_{A\mathop B\limits^\Delta C}}\quad \left( {ii} \right)\\\\\mathop \Rightarrow \limits^{\left( i \right),\left( {ii} \right)} \quad {S_{M\mathop N\limits^\Delta B}} = \frac{1}{6}\left( {\frac{1}{2}{S_{A\mathop {BC}\limits^{} D}}} \right) = \frac{1}{{12}}{S_{A\mathop {BC}\limits^{} D}}\end{array}\)
7 در مثلث ABC، خط MN موازی ضلع BC است و \(\frac{{AM}}{{MB}} = \frac{1}{2}\) همچنین \(\frac{{PC}}{{PB}} = \frac{1}{3}\) است \({S_{AQN}}\) و \({S_{MQPB}}\) چه کسری از مساحت مثلث ABC است؟
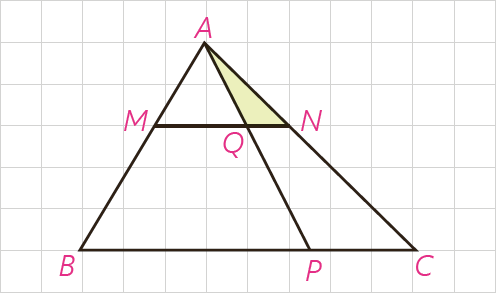
\(\begin{array}{l}\frac{{PC}}{{PB}} = \frac{1}{3} \Rightarrow \frac{{PC}}{{BC}} = \frac{1}{4}\\\\ \Rightarrow \frac{{{S_{A\mathop P\limits^\Delta C}}}}{{{S_{A\mathop B\limits^\Delta C}}}} = \frac{1}{4} \Rightarrow {S_{A\mathop B\limits^\Delta C}} = 4{S_{A\mathop P\limits^\Delta C}}\quad \left( i \right)\\\\A\mathop B\limits^\Delta C:\quad MN\parallel BC \Rightarrow \left\{ \begin{array}{l}\frac{{AN}}{{AC}} = \frac{{AM}}{{AB}} = \frac{1}{3}\\A\mathop Q\limits^\Delta N \sim A\mathop P\limits^\Delta C\end{array} \right.\\\\ \Rightarrow \frac{{{S_{A\mathop Q\limits^\Delta N}}}}{{{S_{A\mathop P\limits^\Delta C}}}} = {\left( {\frac{1}{3}} \right)^2} = \frac{1}{9} \Rightarrow {S_{A\mathop P\limits^\Delta C}} = 9{S_{A\mathop Q\limits^\Delta N}}\quad \left( {ii} \right)\\\\\mathop \Rightarrow \limits^{\left( i \right),\left( {ii} \right)} \quad {S_{A\mathop B\limits^\Delta C}} = 4\left( {4{S_{A\mathop Q\limits^\Delta N}}} \right) = 36{S_{A\mathop Q\limits^\Delta N}}\\\\ \Rightarrow \frac{{{S_{A\mathop Q\limits^\Delta N}}}}{{{S_{A\mathop B\limits^\Delta C}}}} = \frac{1}{{36}}\end{array}\)
\(\begin{array}{l}\frac{{PB}}{{BC}} = \frac{3}{4} \Rightarrow \frac{{{S_{A\mathop P\limits^\Delta B}}}}{{{S_{A\mathop B\limits^\Delta C}}}} = \frac{3}{4} \Rightarrow {S_{A\mathop P\limits^\Delta B}} = \frac{3}{4}{S_{A\mathop B\limits^\Delta C}}\quad \left( i \right)\\\\A\mathop B\limits^\Delta C:\quad MQ\parallel BP \Rightarrow A\mathop Q\limits^\Delta M \sim A\mathop P\limits^\Delta B\\\\ \Rightarrow \frac{{{S_{A\mathop Q\limits^\Delta M}}}}{{{S_{A\mathop B\limits^\Delta P}}}} = {\left( {\frac{1}{3}} \right)^2} = \frac{1}{9} \Rightarrow {S_{A\mathop B\limits^\Delta P}} = 9{S_{A\mathop Q\limits^\Delta M}}\\\\ \Rightarrow {S_{BPQM}} = \frac{8}{9}{S_{A\mathop B\limits^\Delta P}}\quad \left( {ii} \right)\\\\\mathop \Rightarrow \limits^{\left( i \right),\left( {ii} \right)} \quad {S_{BPQM}} = \frac{8}{9}\left( {\frac{3}{4}{S_{A\mathop B\limits^\Delta C}}} \right) = \frac{2}{3}{S_{A\mathop B\limits^\Delta C}}\\\\ \Rightarrow \frac{{{S_{BPQM}}}}{{{S_{A\mathop B\limits^\Delta C}}}} = \frac{2}{3}\end{array}\)
8 با توجه به مساحت چندضلع یهای شبکه ای، مساحت قسمت سایه زده را محاسبه کنید. (راهنمایی: مساحت چند ضلعی داخلی را از مساحت چند ضلعی بیرونی کم کنید.)
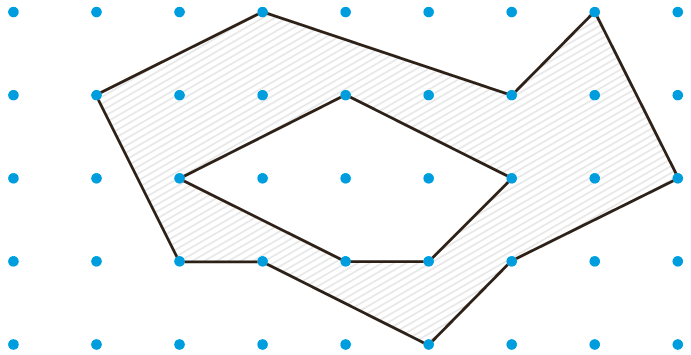
\(\begin{array}{l}\left. \begin{array}{l}\left. \begin{array}{l}{b_1} = 9\\{i_1} = 13\end{array} \right\} \Rightarrow {S_1} = \frac{{{b_1}}}{2} - 1 + {i_1} = \frac{{33}}{2}\\\left. \begin{array}{l}{b_2} = 5\\{i_2} = 3\end{array} \right\} \Rightarrow {S_2} = \frac{{{b_2}}}{2} - 1 + {i_2} = \frac{9}{2}\end{array} \right\}\\\\ \Rightarrow S = {S_1} - {S_2} = 12\end{array}\)
9 یک مستطیل شبکه ای با ضل عهای افقی و قائم که اندازه های ضل عهای آن m و n واحداند مفروض است. مساحت آن را ابتدا به روش معمول و سپس به کمک فرمول پیک محاسبه و آنها را مقایسه کنید.
مساحت به روش معمول : \(S = m \times n\)
مساحت به روش قضیه پیک :
\(\begin{array}{l}b = 2m + 2n\\\\i = \left( {m + 1} \right) \times \left( {n + 1} \right) - \left( {2m + 2n} \right)\\ = mn - m - n + 1\\\\S = \frac{b}{2} - 1 + i = \frac{{2m + 2n}}{2}\\\\ - 1 + \left( {mn - m - n + 1} \right)\\\\ = m + n - 1 + mn - m - n + 1\\\\ = mn = m \times n\end{array}\)
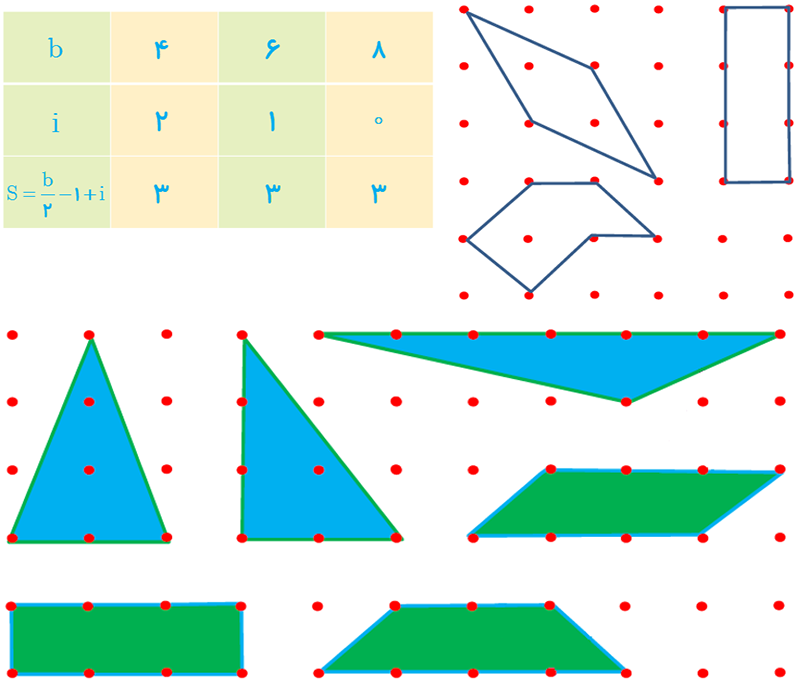
10 مساحت یک چندضلعی شبکه ای 3 واحد است. جدولی تشکیل دهید و تعداد نقاط مرزی و تعداد نقاط درونی را در حالت هایی که امکان دارد، مشخص کنید. اگر این چندضلعی شبکه ای مثلث باشد در هر حالت شکل آن را رسم کنید. در حالتی که نقاط مرزی بیشترین تعداد ممکن را دارند، شکل های چهارضلعی های نظیر آن را نیز رسم کنید.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















