جواب تمرین صفحه 52 درس 2 ریاضیات گسسته (گراف و مدل سازی)
تعداد بازدید : 84.73Mپاسخ تمرین صفحه 52 ریاضیات گسسته
-گام به گام تمرین صفحه 52 درس گراف و مدل سازی
-تمرین صفحه 52 درس 2
-شما در حال مشاهده جواب تمرین صفحه 52 ریاضیات گسسته هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
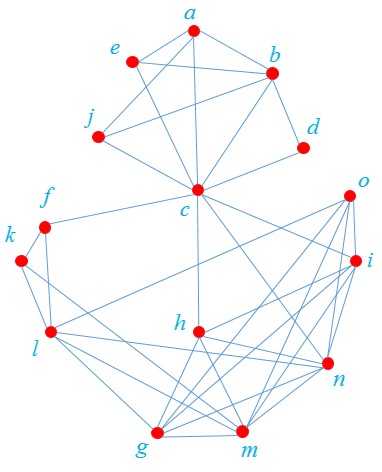
1 در مثال ایستگاه های رادیویی (دومین مثال این درس)
الف تعداد و محل نصب ایستگاه ها را مشخص نمایید.
ب اگر مجبور باشیم یکی از ایستگاه ها را در شهر b احداث کنیم حداقل چند ایستگاه دیگر و در چه شهرهایی باید احداث کنیم؟
الف
حداقل سه ایستگاه باید نصب شود که می توان آن ایستگاه ها را به صورت\(\left\{ {g\;,\;a\;,\;k} \right\}\) یا\(\left\{ {f\;,\;d\;,\;j} \right\}\) یا\(\left\{ {g\;,\;b\;,\;i} \right\}\) یا\(\left\{ {d\;,\;c\;,\;i} \right\}\) یا ... انتخاب کرد.
ب
حداقل دو ایستگاه دیگر باید احداث نمود. این دو ایستگاه می تواند\(\left\{ {g\;,\;i} \right\}\) یا\(\left\{ {f\;,\;k} \right\}\) یا ... باشد.
٢ نقشه مقابل نقشه یک منطقه شامل چند روستا و جاده های بین آن روستاهاست و مسافت جاده های بین روستاها در آن مشخص شده است. قصد داریم چند بیمارستان مجهز در برخی روستاها احداث کنیم به گونه ای که فاصله هر روستا تا نزدیکترین بیمارستان به آن روستا از 10 کیلومتر بیشتر نباشد و از طرفی کمترین تعداد ممکن بیمارستان را احداث کنیم. ابتدا با توجه به نقشه فوق، مسئله مورد نظر را با یک گراف مناسب مدلسازی کنید و سپس تعداد و محل احداث بیمارستانها را مشخص کنید.
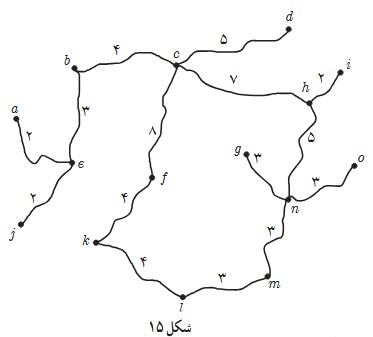
ابتدا هر روستا را به عنوان یک رأس گراف (با حرف کوچک انگلیسی) مشخص می کنیم، سپس بین دو رأس (دو روستا) به شرطی یال رسم می کنیم که فاصله ی بین آن دو بیشتر از 10 کیلومتر نباشد.
\(\gamma (G) \ge \left[ {\frac{{15}}{{8 + 1}}} \right] + 1 = 2\)
یک مجموعه احاطه گری می تواند\(\left\{ {c\;,\;m} \right\}\) باشد، بنابراین کافیست دو بیمارستان در روستاهای\(c\) و\(m\) احداث کرد.
3 عدد احاطه گری را برای هر یک از گراف های زیر مشخص نمایید.
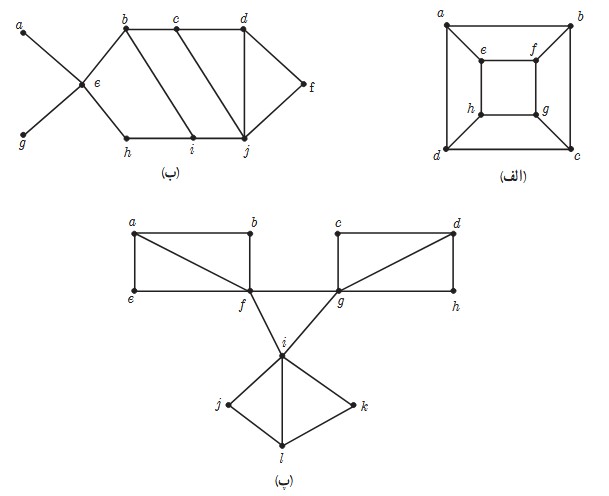
الف
\(\gamma (G) \ge \left[ {\frac{8}{{3 + 1}}} \right] = 2\)
مجموعه \(\left\{ {a\;,\;g} \right\}\) یک مجموعه احاطه گری برای آن است؛ بنابراین: \(\gamma (G) = 2\)
ب
\(\gamma (G) \ge \left[ {\frac{{10}}{{4 + 1}}} \right] = 2\)
مجموعه \(\left\{ {e\;,\;j} \right\}\) یک مجموعه احاطه گری برای آن است؛ بنابراین: \(\gamma (G) = 2\)
پ
\(\gamma (G) \ge \left[ {\frac{{12}}{{5 + 1}}} \right] = 2\)
مجموعه \(\left\{ {f\;,\;d\;,\;l} \right\}\) یک مجموعه احاطه گری برای آن است؛ بنابراین: \(\gamma (G) = 2\)
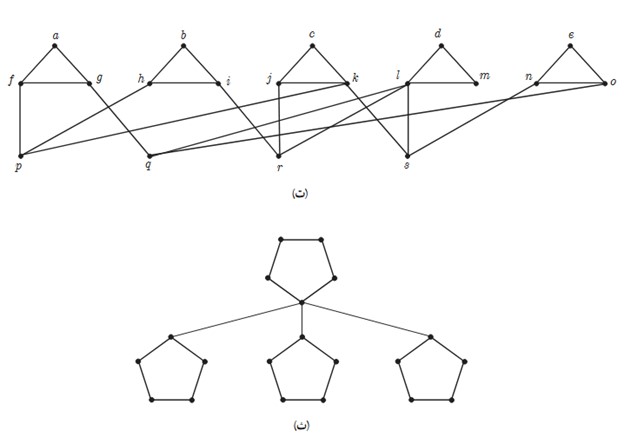
ت
\(\gamma (G) \ge \left[ {\frac{{19}}{{5 + 1}}} \right] + 1 = 4\)
از طرفی از هر مثلث حداقل یک رأس باید انتخاب کنیم، به عنوان نمونه مجموعه \(\left\{ {f\;,\;i\;,\;k\;,\;l\;,\;e} \right\}\) یک مجموعه احاطه گری برای آن است؛ بنابراین: \(\gamma (G) = 5\)
ث
\(\gamma (G) \ge \left[ {\frac{{20}}{{5 + 1}}} \right] + 1 = 4\)
از طرفی از هر پنج ضلعی حداقل دو رأس باید انتخاب کنیم، لذا 8=2×4 یعنی \(\gamma (G) = 8\) به عنوان نمونه، رئوس قرمز رنگ به عنوان یک مجموعه احاطه گری محسوب می شوند.
4 اگر برای گراف G داشته باشیم\(\gamma \left( G \right) = 1\) ، در این صورت به چه ویژگی هایی از گراف G می توان پی برد؟ ((G)∆ و حداقل و حداکثر تعداد یال هایی را که گراف G می تواند داشته باشد مشخص کنید).
حداقل یک رأس با ماکزیمم درجه (رأس فول) وجود دارد. با فرض اینکه گراف دارای\(n \) رأس باشد، حداقل باید\(n - 1\) یال داشته باشد که می توان شکل مقابل را برای آن پیشنهاد کرد.
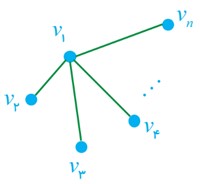
حداقل میزان تعداد یال\(\frac{{n(n - 1)}}{2}\) می باشد ( حالتی که گراف کامل باشد)، در هر صورت\(\Delta \;(G) = n - 1\) است.
5 \(\gamma \left( {{C_n}} \right)\;,\;\gamma \left( {{P_n}} \right)\) را به ازای هر\(n \in N\) مشخص کنید.
با توجه به اینکه در هر دو، حداکثر درجه رئوس 2 می باشد، داریم:
\(\gamma \;({P_n}) = \gamma \;({C_n}) = \left[ {\frac{n}{{1 + 2}}} \right] = \left[ {\frac{n}{3}} \right]\)
6 اگر G یک گراف \(-k\) منتظم n رأسی باشد نشان دهید \(\left[ {\frac{n}{{k + 1}}} \right] \le \gamma \left( G \right)\)
در گراف \(-k\) منتظم n رأسی، \(\Delta = \delta = k\) می باشد، بنابراین: \(\gamma \;(G) \ge \left[ {\frac{n}{{k + 1}}} \right]\)
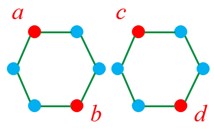
7 یک گراف 2ــ منتظم 12 رأسی بکشید که عدد احاطه گری آن کمترین مقدار ممکن باشد.
\(\gamma \;(G) \ge \left[ {\frac{{12}}{{2 + 1}}} \right] = 4\) ، مجموعه ی\(\left\{ {a\;,\;b\;,\;c\;,\;d} \right\}\) یک مجموعه ی احاطه گری است، بنابراین عدد احاطه گری آن 4 می باشد:
8 الف یک گراف 6 رأسی که \(-γ \) مجموعه آن با اندازه یک باشد رسم کنید.
ب یک گراف 6 رأسی که \(-γ \) مجموعه آن با اندازه دو باشد رسم کنید.
پ فرض کنید n و k دو عدد طبیعی باشند و\(k \le \frac{n}{2}\) روشی برای رسم یک گراف n رأسی که عدد احاطه گری آن k باشد، ارائه دهید.
الف
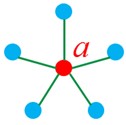
مجموعه احاطه گری گراف روبرو\(\left\{ a \right\}\) است.
ب
در گراف مقابل مجموعه احاطه گری\(\left\{ {a\;,\;b} \right\}\) است.

پ
کافیست گراف را به صورت k بخشی رسم کنیم و در هر بخش رأسی که همه ی رئوس آن بخش را احاطه می کند، در نظر بگیریم.
9 الف یک گراف 6 رأسی با عدد احاطه گری 2 رسم کنید که یک مجموعه احاطه گر یکتا با اندازه 2 داشته باشد.
ب یک گراف 6 رأسی با عدد احاطه گری 2 رسم کنید که بیش از یک مجموعه احاطه گر با اندازه 2 داشته باشد.
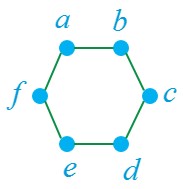
الف
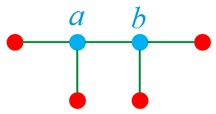
مجموعه احاطه گری آن \(\left\{ {a\;,\;b} \right\}\) است.
ب
گراف مقابل دارای سه مجموعه ی احاطه گری به اندازه 2 می باشد، که عبارتند از:
\(\left\{ {a\;,\;d} \right\}\) و \(\left\{ {f\;,\;c} \right\}\) و \(\left\{ {e\;,\;b} \right\}\)
10 برای هر\(\left( {n \ge 4} \right)\;\;n \in N\) دلخواه توضیح دهید که
الف چگونه می توانید یک گراف n رأسی با عدد احاطه گری 2 رسم کنید که یک مجموعه احاطه گر یکتا با اندازه 2 داشته باشد.
ب چگونه می توانید یک گراف n رأسی با عدد احاطه گری 2 رسم کنید که بیش از یک مجموعه احاطه گر با اندازه 2 داشته باشد.
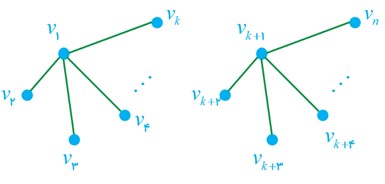
الف
کافیست مطابق شکل روبرو، یک گراف دو بخشی رسم کنیم به طوری که یک بخش آن شامل k رأس و بخش آن شامل n-k رأس باشد.
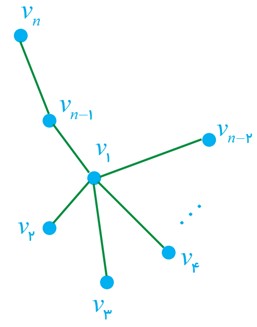
ب
مطابق شکل روبرو باید گراف را رسم کرد که دو مجموعه ی احاطه گری آن\(\left\{ {{v_1}\;,\;{v_n}} \right\}\) و\(\left\{ {{v_1}\;,\;{v_{n - 1}}} \right\}\) می باشند.
11 گراف P12 را رسم کنید.
الف یک γــ مجموعه از آن را مشخص نمایید.
ب یک مجموعه احاطه گر مینیمال 6 عضوی از آن را مشخص نمایید.

الف
مجموعه\(\left\{ {b\;,\;e\;,\;h\;,\;k} \right\}\) یک 4- مجموعه است.
ب
مجموعه\(\left\{ {b\;,\;c\;,\;f\;,\;g\;,\;j\;,\;k} \right\}\) یک مجموعه احاطه گر مینیمال 6 عضوی است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















