جواب فعالیت صفحه 50 درس 2 ریاضیات گسسته (گراف و مدل سازی)
تعداد بازدید : 84.72Mپاسخ فعالیت صفحه 50 ریاضیات گسسته
-گام به گام فعالیت صفحه 50 درس گراف و مدل سازی
-فعالیت صفحه 50 درس 2
-شما در حال مشاهده جواب فعالیت صفحه 50 ریاضیات گسسته هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 می خواهیم عدد احاطه گری گراف شکل 12 را مشخص کنیم.
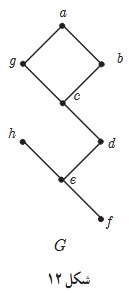
الف ابتدا میبینیم که با توجه به کران پایین\(\left[ {\frac{n}{{\Delta + 1}}} \right]\) برای \(γ(G)\)حداقل احاطه کردن رئوس لازم است اما در مراحل بعدی میبینیم که 2 رأس برای احاطه تمام رئوس این گراف کافی نیست.
ب برای احاطه کردن رأس h حداقل یکی از رئوس e یا h باید در مجموعه احاطه گر باشند و با بودن هر کدام از آنها در مجموعه احاطه گر، رئوس g,c,b,a کماکان احاطه نشده باقی می مانند.
پ برای احاطه کردن رئوس g,c,b,a حداقل دو رأس دیگر نیاز هست، زیرا هیچ رأسی به تنهایی نمی تواند هر چهارتای آنها را احاطه کند.
ت بنابراین حداقل 3 رأس باید در هر مجموعه احاطه گر از گراف G باشد یعنی \(\gamma \left( G \right) \ge 3\)
ث از طرفی چون {a, c, e} یک مجموعه احاطه گر است،\(\gamma \left( G \right) \le 3\) پس \(\gamma \left( G \right) = 3\)
ب
زیرا \(\left[ {\frac{5}{{3 + 1}}} \right] + 1 = 2\)
پ
زیرا \(\left[ {\frac{3}{{3 + 1}}} \right] + 1 = 1\)
٢ می خواهیم عدد احاطه گر گراف شکل 13 را مشخص نماییم.
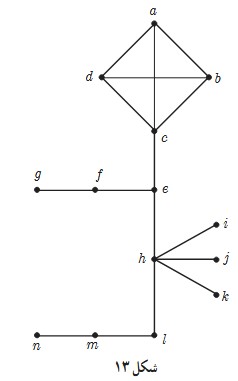
الف ابتدا کران پایین\(\left[ {\frac{n}{{\Delta + 1}}} \right]\) را بررسی می کنیم که عدد\(\left[ {\frac{{14}}{6}} \right] = 3\) می دهد. پس \(\gamma \left( G \right) \ge 3\)
ب اما حداقل یکی از رئوس a ، b ، c و d باید انتخاب شود. چرا؟
پ حداقل یکی از رئوس f و g باید انتخاب شود. چرا؟
ت حداقل یکی از رئوس i و h باید انتخاب شود. چرا؟
ث حداقل یکی از رئوس m و n باید انتخاب شود. چرا؟
ج بنابراین حداقل 4 رأس در هر مجموعه احاطه گر باید باشد. لذا\(\gamma \left( G \right) \ge 4\) و با توجه به اینکه {c,f,h,m} یک مجموعه احاطه گر است لذا\(\gamma \left( G \right) \le 4\) بنابراین\(\gamma \left( G \right) = 4\) .
ب
زیرا \(\left[ {\frac{4}{{4 + 1}}} \right] + 1 = 1\)
پ
زیرا \(\left[ {\frac{3}{{3 + 1}}} \right] + 1 = 1\)
ت
زیرا \(\left[ {\frac{4}{{5 + 1}}} \right] + 1 = 1\)
ث
زیرا \(\left[ {\frac{3}{{2 + 1}}} \right] = 1\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















