جواب فصل 3 توابع نمایی و لگاریتمی حسابان یازدهم
تعداد بازدید : 3.13Mپاسخ به تمامی سوالات فصل توابع نمایی و لگاریتمی - حل المسائل فصل 3 توابع نمایی و لگاریتمی - گام به گام 1401 کتاب حسابان یازدهم - گام به گام کتاب حسابان یازدهم مطابق با آخرین تغییرات کتب درسی
فعالیت صفحه 72 درس توابع نمایی و لگاریتمی حسابان یازدهم
پاسخ فعالیت صفحه 72 درس 3
جواب فعالیت صفحه 72 درس 3 حسابان یازدهم
یک توده باکتری را در محیط کشت در نظر بگیرید. فرض کنید با نمونه گیری از این جامعه، مشخص شده است که جرم باکتری ها در هر ساعت دو برابر می شود. اگر جرم باکتری ها را پس از t ساعت با m(t) نشان دهیم و با 1 گرم شروع کنیم یعنی m(0)=1، آن گاه باتوجه به جدول، به پرسش های زیر پاسخ دهید.
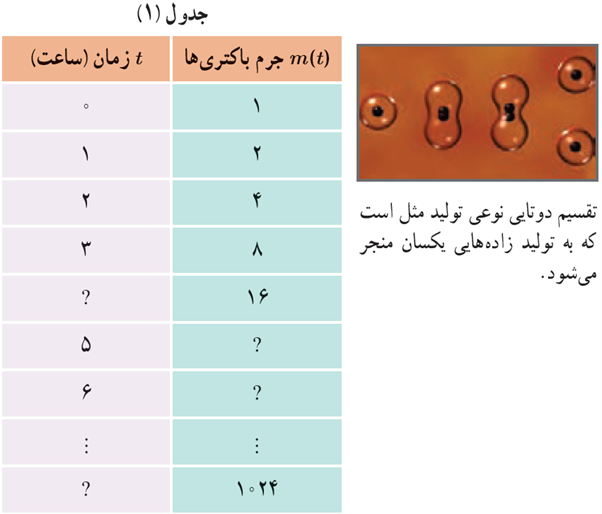
الف در زمان های t=6 و t=5 جرم باکتری ها را به دست آورید.
ب پس از چند ساعت جرم باکتری ها 256 گرم می شود؟ پس از چند ساعت به 1024 گرم می رسد؟
پ آیا از اعداد این جدول می توان الگویی را برای محاسبه جرم باکتری ها در هر زمان به دست آورد؟
اگر بخواهیم جرم باکتری ها را در مرحلهٔ یازدهم یا مرحله ای بالاتر پیدا کنیم، قطعاً محاسبات، خیلی دشوارتر و وقت گیر خواهد شد. برای ساده تر شدن محاسبات، جدول (1) را بر اساس توان های 2، بازنویسی می کنیم تا جدول (2) حاصل شود. در جدول (2) به جای علامت سؤال ها اعداد مناسب قرار دهید.

الف
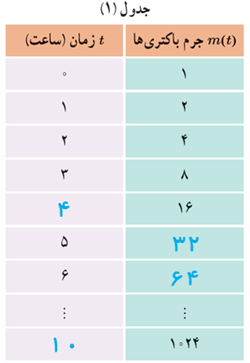
\(\begin{array}{l}m\left( 5 \right) = 32\\m\left( 6 \right) = 64\end{array}\)
ب
\(\begin{array}{l}m\left( t \right) = 256 \Rightarrow t = 8\\m\left( t \right) = 1024 \Rightarrow t = 10\end{array}\)
پ
\(m\left( t \right) = {2^t}\)

مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
فعالیت صفحه 73 درس توابع نمایی و لگاریتمی حسابان یازدهم
پاسخ فعالیت صفحه 73 درس 3
جواب فعالیت صفحه 73 درس 3 حسابان یازدهم
در نمودار فعالیت قبل، طول نقاط مشخص شده اعداد صحیح نامنفی هستند. می توان نقاطی از آن نمودار، با طول اعداد گویا را نیز به دست آورد.
الف جاهای خالی جدول را با قرار دادن اعداد مناسب پر کنید.
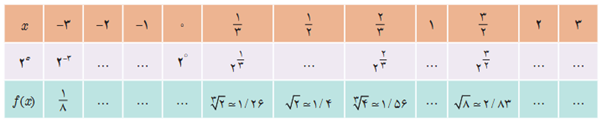
ب نقاط به دست آمده را در یک صفحهٔ شطرنجی مشخص کنید (برخی از نقاط در دستگاه مشخص شده اند).
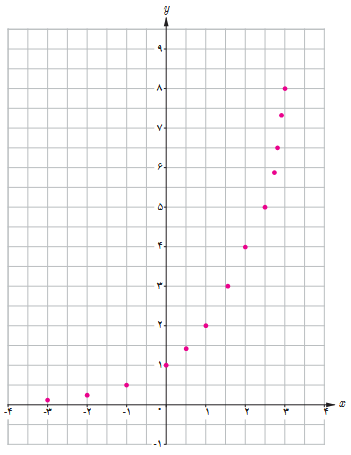
همان طور که ملاحظه می شود دامنهٔ تابع \(y = {2^x}\) همهٔ اعداد حقیقی و برد آن همواره اعداد مثبت است.
اگر تعداد نقاط خیلی زیاد شوند، شکلی شبیه نمودار روبه رو حاصل می شود.
پ چرا نمودار روبه رو یک تابع است؟
ت نقطۀ \(x = \sqrt 2 \) را روی محور xها مشخص کنید، سپس مقدار تقریبی \({2^{\sqrt 2 }}\) را با استفاده از نمودار پیدا کنید.
ث کدام یک از اعداد زیر، بین دو عدد 23 و 22 قرار دارد؟
\(\begin{array}{l}{2^{\frac{5}{2}}}\;\;\;\;\;{2^{\frac{3}{2}}}\\\\{2^5}\;\;\;\;\;{2^{ - 1}}\end{array}\)
ج چرا نمودار تابع \(y = {2^x}\) محور xها را قطع نمی کند؟
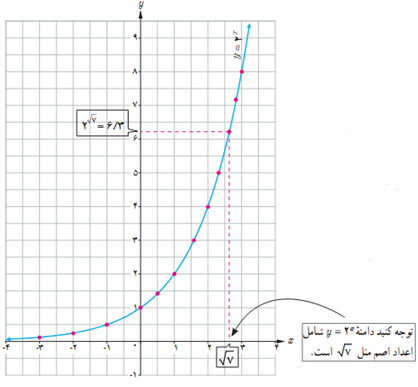
الف

ب
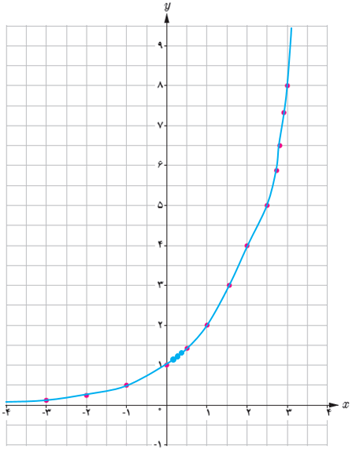
پ
اگر خطی موازی محور y رسم کنیم، نمودار را حداکثر در یک نقطه قطع می کند.
ت
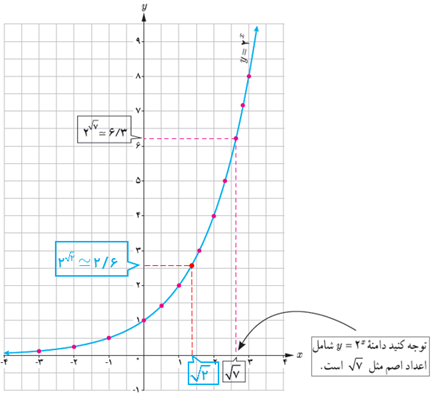
ث
\({2^{\frac{5}{2}}}\)
ج
چرا که هر چه به سمت چپ محور x برویم، نمودار فقط به این محور نزدیک می شود. همچنین هنگامی تابع \(y = {2^x}\) به صفر می رسد که توان عدد 2 ، منفی بینهایت (\( - \;\infty \)) باشد.
گام به گام کتاب های پایه یازدهم
گام به گام جامع کتاب حسابان یازدهم
گام به گام جامع کتاب فیزیک یازدهم ریاضی
گام به گام جامع کتاب شیمی یازدهم
گام به گام جامع کتاب هندسه یازدهم
گام به گام جامع کتاب آمار و احتمال یازدهم ریاضی
گام به گام جامع کتاب زمین شناسی
گام به گام جامع کتاب فارسی یازدهم
گام به گام جامع کتاب نگارش یازدهم
گام به گام جامع کتاب عربی یازدهم
گام به گام جامع کتاب زبان انگلیسی یازدهم
گام به گام جامع کتاب کتاب کار انگلیسی یازدهم
گام به گام جامع کتاب انسان و محیط زیست
گام به گام جامع کتاب دین و زندگی یازدهم
گام به گام جامع کتاب آزمایشگاه علوم تجربی یازدهم
گام به گام جامع کتاب تاریخ معاصر ایران
کاردرکلاس صفحه 75 درس توابع نمایی و لگاریتمی حسابان یازدهم
پاسخ کاردرکلاس صفحه 75 درس 3
جواب کاردرکلاس صفحه 75 درس 3 حسابان یازدهم
الف نمودار تابع \(y = {\left( {\frac{1}{2}} \right)^x}\) را رسم کنید و آن را با نمودار \(y = {2^x}\) مقایسه کنید.
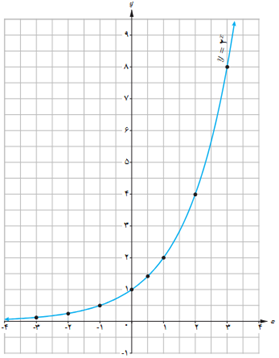
ب دامنه و برد تابع را به دست آورید.
پ نقطه \(\left( {0/5\;,\;{{\left( {\frac{1}{2}} \right)}^{0/5}}} \right)\) را روی نمودار مشخص کنید.
الف و پ
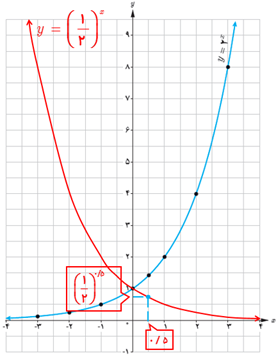
نسبت به محور y متقارن است.
ب
\(\left\{ \begin{array}{l}D = \mathbb{R}\\R = \left( {0\;,\;\infty } \right)\end{array} \right.\)
کاردرکلاس صفحه 76 درس توابع نمایی و لگاریتمی حسابان یازدهم
پاسخ کاردرکلاس صفحه 76 درس 3
جواب کاردرکلاس صفحه 76 درس 3 حسابان یازدهم
1 نمودارهای سه تابع \(h(x) = {5^x}\,,\,g(x) = {3^x}\,,\,f(x) = {2^x}\) در شکل (1) رسم شده اند. ضابطه هر تابع را روی نمودار آن بنویسید.
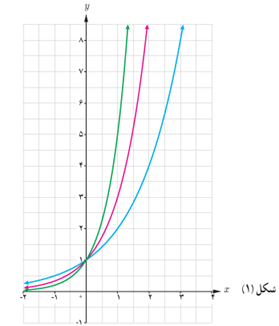
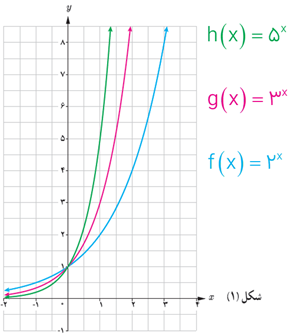
2 دامنه و برد هر تابع را بنویسید.
\(\begin{array}{l}h\left( x \right) = {5^x}\\\left\{ \begin{array}{l}D = \mathbb{R}\\R = \left( {0\;,\;\infty } \right)\end{array} \right.\\\\g\left( x \right) = {3^x}\\\left\{ \begin{array}{l}D = \mathbb{R}\\R = \left( {0\;,\;\infty } \right)\end{array} \right.\\\\f\left( x \right) = {2^x}\\\left\{ \begin{array}{l}D = \mathbb{R}\\R = \left( {0\;,\;\infty } \right)\end{array} \right.\end{array}\)
3 آیا این توابع یک به یک هستند؟ چرا؟
بله؛ زیرا هر خطی موازی محور x رسم شود، توابع را حداکثر در یک نقطه قطع می کند.
4 نمودارهای توابع \(v\left( x \right) = {\left( {\frac{1}{3}} \right)^x}\;,\;u\left( x \right) = {\left( {\frac{1}{2}} \right)^x}\) و \(t\left( x \right) = {\left( {\frac{1}{5}} \right)^x}\) در شکل (2) رسم شده اند. ابتدا ضابطه هر یک را روی نمودار آن بنویسید و سپس دامنه و برد آنها را به دست آورید. آیا این توابع یک به یک هستند؟
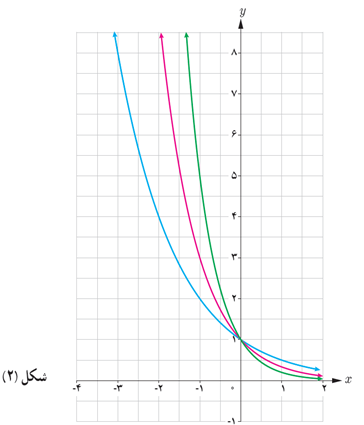
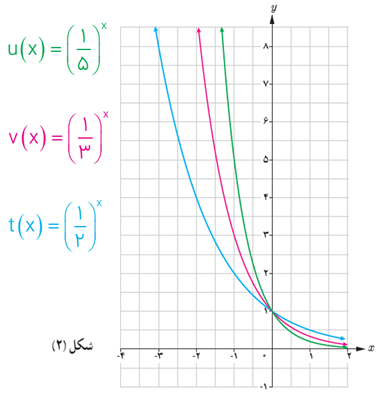
\(\begin{array}{l}u\left( x \right) = {\left( {\frac{1}{5}} \right)^x}\\\left\{ \begin{array}{l}D = \mathbb{R}\\R = \left( {0\;,\;\infty } \right)\end{array} \right.\\\\v\left( x \right) = {\left( {\frac{1}{3}} \right)^x}\\\left\{ \begin{array}{l}D = \mathbb{R}\\R = \left( {0\;,\;\infty } \right)\end{array} \right.\\\\t\left( x \right) = {\left( {\frac{1}{2}} \right)^x}\\\left\{ \begin{array}{l}D = \mathbb{R}\\R = \left( {0\;,\;\infty } \right)\end{array} \right.\end{array}\)
بله؛ این توابع نیز یک به یک هستند.
5
الف اعداد مقابل را از کوچک به بزرگ مرتب کنید:
\({2^4}\;,\;{\left( {\frac{1}{2}} \right)^2}\;,\;{2^2}\;,\;{2^3}\;,\;{\left( {\frac{1}{2}} \right)^4}\;,\;{\left( {\frac{1}{2}} \right)^3}\)
ب جاهای خالی را پر کنید:
در تابع \(f\left( x \right) = {a^x}\) ،
- اگر \(a>1\)، با افزایش مقدار x، مقادیر f ........ می یابند.
- اگر \(0<a<1\)، با افزایش مقدار x، مقادیر تابع f ........ می یابند.
الف
\({\left( {\frac{1}{2}} \right)^4}\;,\;{\left( {\frac{1}{2}} \right)^3}\;,\;{\left( {\frac{1}{2}} \right)^2}\;,\;{2^2}\;,\;{2^3}\;,\;{2^4}\)
ب
- افزایش
- کاهش
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
تمرین صفحه 77 درس توابع نمایی و لگاریتمی حسابان یازدهم
پاسخ تمرین صفحه 77 درس 3
جواب تمرین صفحه 77 درس 3 حسابان یازدهم
1 تحت شرایط ایده آل، جرم یک تودهٔ معین از باکتری ها در هر ساعت دو برابر می شود. فرض کنید در ابتدا 100 میلی گرم باکتری وجود دارد.
الف جرم توده پس از t ساعت را به صورت یک تابع نمایی بنویسید.
ب جرم توده را پس از 20 ساعت برآورد کنید.
الف
\(m\left( t \right) = 100{\left( 2 \right)^t}\)
ب
\(t = 20 \Rightarrow m\left( {20} \right) = 100{\left( 2 \right)^{20}}\)
2 نمودار توابع \(y = {2^x} - 1\;\;,\;y = {2^x} + 1\;\;,\;\;y = {2^x}\) در شکل روبه رو آمده اند. ضابطه هر تابع را روی آن مشخص کنید. با مقایسه نمودارهای توابع \(y = {a^x} - 2\;\;,\;\;y = {a^x} + 2\;\;,\;\;y = {a^x}\) با یکدیگر چه نتیجه ای می گیرید؟ (a>1)
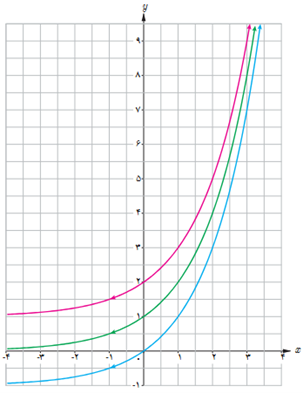
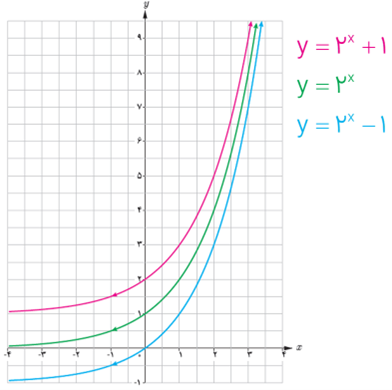
ابتدا نمودار \(y = {a^x}\) را رسم می کنیم و سپس 2 واحد آن را در جهت بالا انتقال می دهیم و در این صورت نمودار \(y = {a^x} + 2\) بدست می آید و اگر نمودار \(y = {a^x}\) را 2 واحد به سمت پایین انتقال دهیم، نمودار\(y = {a^x} - 2\) رسم می شود.
3 داروها در بدن با ادرار دفع می شوند. فرض کنید 10 میلی گرم از یک نوع دارو در بدن شخصی قرار دارد و مقدار آن پس از t ساعت از رابطه \(A\left( t \right) = 10{\left( {0/8} \right)^t}\) به دست می آید.
الف مقدار دارو پس از 8 ساعت چقدر است؟
ب چه درصدی از دارو در هر ساعت از بین می رود؟
الف
\(A\left( 8 \right) = 10{\left( {0/8} \right)^8} \simeq 1/7\)
ب
\(\begin{array}{l}\left| {\frac{{A\left( {t + 1} \right) - A\left( t \right)}}{{A\left( t \right)}}} \right| \times 100 = \left| {\frac{{10{{\left( {0/8} \right)}^{t + 1}} - 10{{\left( {0/8} \right)}^t}}}{{10{{\left( {0/8} \right)}^t}}}} \right| \times 100\\\\ = \left| {\frac{{0/8 - 1}}{1}} \right| \times 100 = 20\% \end{array}\)
4
الف سه عدد بین اعداد\({3^{2/5}}\) و \({3^{\sqrt {10} }}\) پیدا کنید.
ب نامعادلهٔ توانی \({4^{2a - 1}} > \frac{1}{{1024}}\) را حل کنید.
پ اگر y، x و z سه عدد حقیقی باشند، به طوری که \({a^x} > {a^y} > {a^z}\) ، آن گاه چه رابطه ای بین x و y و z برقرار است؟ (a>1)
الف
\(\sqrt {10} \simeq 3/1\quad \Rightarrow \quad {3^{2/5}}\;,\;{3^{2/6}}\;,\;{3^{2/8}}\;,\;{3^3}\;,\;{3^{\sqrt {10} }}\)
ب
\({4^{2x - 1}} > \frac{1}{{1024}} = \frac{1}{{4{}^5}} = {4^{ - 5}} \Rightarrow 2x - 1 > - 5 \Rightarrow x > - 2\)
پ
\(x > y > z\)
5 ابتدا مقدار تقریبی هر عدد را به کمک نمودار پیدا کنید. سپس به کمک ماشین حساب، درستی پاسخ خود را بررسی کنید.
الف \({3^{1 - \sqrt 2 }}\)
ب \({2^{1/25}}\)
پ \({3^{\frac{3}{2}}}\)
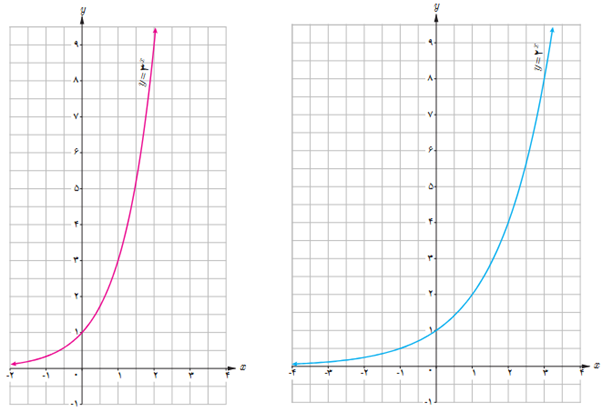
الف
\({3^{1 - \sqrt 2 }} \simeq 0/63\)
ب
\({2^{1/25}} \simeq 2/37\)
پ
\({3^{\frac{3}{2}}} \simeq 5/2\)
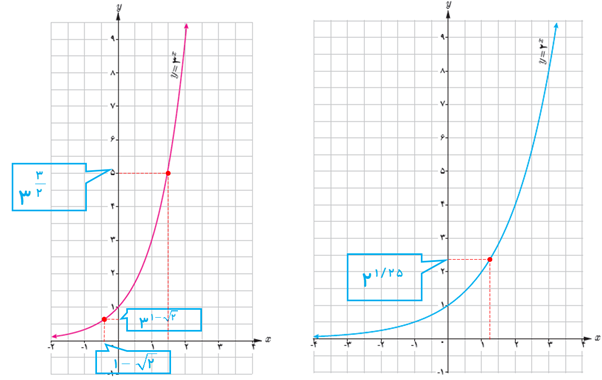
6 الف در شکل زیر خط \(y = \frac{{13}}{2}\) نمودار\(y = {2^x}\) راقطع کرده است. طول نقطه برخورد بین کدام دو عدد صحیح قرار دارد؟چرا؟
ب خط \(y = \sqrt 7 \) را رسم کنید. طول نقطه برخورد این خط و نمودار \(y = {2^x}\) بین کدام دو عدد صحیح قرار دارد؟

الف
بین دو عدد 2 و 3 ؛ زیرا : \({2^2} < \frac{{13}}{2} < {2^3}\)
ب

بین دو عدد 1 و 2.
7 در تصفیهٔ آب، داخل فیلترها، لایهٔ تمیز کننده ای قرار دارد که حدود 30 درصد از ناخالصی ها را حذف می کند و در نتیجه 70 درصد از ناخالصی ها باقی می ماند. اگر داخل این فیلترها، دو لایه قرار دهیم، آنگاه \(0/7×0/7=0/49\) یا 49 درصد از ناخالصی ها باقی می ماند.
الف درصد ناخالصی های موجود در آب از کدام رابطه به دست می آید؟
ب با قرار دادن چند لایه در فیلتر می توان بیش از 96 درصد از ناخالصی های آب را از بین برد؟
الف
\(0/7 \to 0/7 \times 100 = 70\% \) :یک لایه
\({\left( {0/7} \right)^2} \to 0/49 \times 100 = 49\% \) :دو لایه
\({\left( {0/7} \right)^n} \to {\left( {\frac{7}{{100}}} \right)^n} \times 100 = \frac{{{7^n}}}{{{{100}^{n - 1}}}}\% \) :n لایه
ب
\(\begin{array}{l}100\% - 96\% = 4\% \\\frac{{{7^n}}}{{{{10}^{n - 2}}}}\% < 4\% \Rightarrow \frac{{\frac{{{7^n}}}{{{{10}^{n - 2}}}}}}{{100}} = 0/04\\ \Rightarrow {\left( {0/7} \right)^n} < 0/04 \simeq {\left( {0/7} \right)^9} \Rightarrow n > 9 \Rightarrow n = 10\end{array}\)
گام به گام کتاب های پایه یازدهم
گام به گام جامع کتاب حسابان یازدهم
گام به گام جامع کتاب فیزیک یازدهم ریاضی
گام به گام جامع کتاب شیمی یازدهم
گام به گام جامع کتاب هندسه یازدهم
گام به گام جامع کتاب آمار و احتمال یازدهم ریاضی
گام به گام جامع کتاب زمین شناسی
گام به گام جامع کتاب فارسی یازدهم
گام به گام جامع کتاب نگارش یازدهم
گام به گام جامع کتاب عربی یازدهم
گام به گام جامع کتاب زبان انگلیسی یازدهم
گام به گام جامع کتاب کتاب کار انگلیسی یازدهم
گام به گام جامع کتاب انسان و محیط زیست
گام به گام جامع کتاب دین و زندگی یازدهم
گام به گام جامع کتاب آزمایشگاه علوم تجربی یازدهم
گام به گام جامع کتاب تاریخ معاصر ایران
فعالیت صفحه 81 درس توابع نمایی و لگاریتمی حسابان یازدهم
پاسخ فعالیت صفحه 81 درس 3
جواب فعالیت صفحه 81 درس 3 حسابان یازدهم
1 باتوجه به نمودار تابع \(f\left( x \right) = {3^x}\) نمودار تابع f-1 را رسم کنید و جدول زیر را کامل کنید.

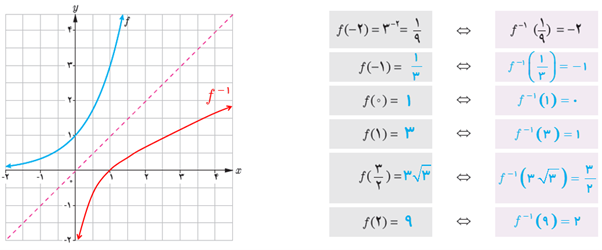
2 گزینهٔ درست را با ✔ و گزینه غلط را با × علامت بزنید.
- نقطۀ \(\left( { - 2\;,\;\frac{1}{9}} \right)\) روی نمودار f قرار دارد.
- نقطۀ \(\left( { - 1\;,\;\frac{1}{3}} \right)\) روی نمودار f-1 قرار دارد.
- نقطۀ \(\left( {1\;,\;0} \right)\) روی نمودار f قرار دارد.
- نقطۀ \(\left( {\frac{1}{9}\;,\; - 2} \right)\) روی نمودار f-1 قرار دارد.
- تابع f-1 یک به یک است.
- نقطۀ \(\left( { - 2\;,\;\frac{1}{9}} \right)\) روی نمودار f قرار دارد. ✔
- نقطۀ \(\left( { - 1\;,\;\frac{1}{3}} \right)\) روی نمودار f-1 قرار دارد. ×
- نقطۀ \(\left( {1\;,\;0} \right)\) روی نمودار f قرار دارد. ×
- نقطۀ \(\left( {\frac{1}{9}\;,\; - 2} \right)\) روی نمودار f-1 قرار دارد. ✔
- تابع f-1 یک به یک است. ✔
کاردرکلاس صفحه 83 درس توابع نمایی و لگاریتمی حسابان یازدهم
پاسخ کاردرکلاس صفحه 83 درس 3
جواب کاردرکلاس صفحه 83 درس 3 حسابان یازدهم
1 الف نمودار سه تابع \(h\left( x \right) = {\log _5}x\;\;,\;\;g\left( x \right) = {\log _3}x\;\;,\;\;f\left( x \right) = {\log _2}x\) در شکل زیر رسم شده اند. ضابطه هریک را روی نمودار آن بنویسید.
ب محل دقیق هریک از نقاط زیر را روی نمودار متناظرش نشان دهید.
(5 , 1) و (9 , 2) و (16 , 4)
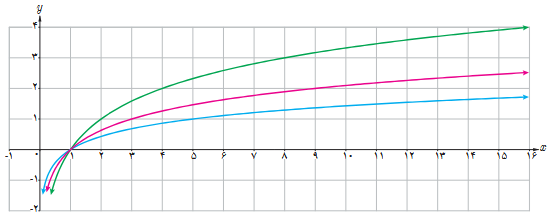
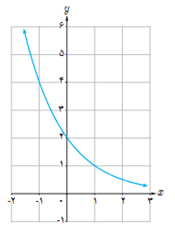
پ با توجه به نمودار \(y = {\left( {\frac{1}{2}} \right)^x}\) نمودار \(y = {\log _{\frac{1}{2}}}x\) را رسم کنید و سپس آنها را با هم مقایسه کنید.
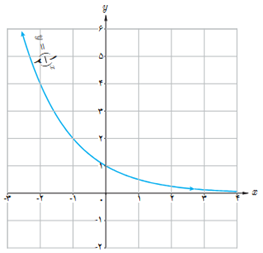
الف و ب
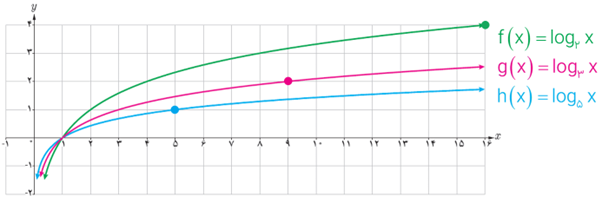
پ
نسبت به خط x=y قرینه اند:

2 مشخص کنید هر یک از نمودارهای زیر به کدام یک از ضابطه های زیر تعلق دارد؟
الف \(y = - {2^x} + 2\)
ب \(y = {\log _2}x + 1\)
پ \(y = {\left( {\frac{1}{2}} \right)^{x - 1}}\)

الف
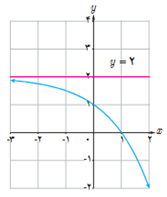
ب
ضابطه (ب) را نمی دهد:
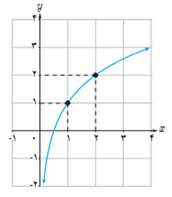
پ
3 حاصل عبارت های زیر را به دست آورید.
الف \({\log _3}81\)
ب \({\log _{\frac{1}{6}}}\frac{1}{6}\)
پ \({\log _2}8\)
الف
\({\log _3}81 = 4\)
ب
\({\log _{\frac{1}{6}}}\frac{1}{6} = 1\)
پ
\({\log _2}8 = 3\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
تمرین صفحه 85 درس توابع نمایی و لگاریتمی حسابان یازدهم
پاسخ تمرین صفحه 85 درس 3
جواب تمرین صفحه 85 درس 3 حسابان یازدهم
1- با استفاده از تعریف لگاریتم، حاصل عبارت های زیر را بیابید:
\({\log _{10}}0/01\;\;,\;\;{\log _6}\frac{1}{6}\;\;,\;\;{\log _2}\sqrt 2 \;\;,\;\;{\log _7}\sqrt[3]{{{7^2}}}\)
\(\begin{array}{l}{\log _{10}}0/01 = - 2\\\\{\log _6}\frac{1}{6} = - 1\\\\{\log _2}\sqrt 2 = \frac{1}{2}\\\\{\log _7}\sqrt[3]{{{7^2}}} = \frac{2}{3}\end{array}\)
2 نمودار تابع \(y = {\log _a}x\) را برای دو حالت \(a>1\) و \(0<a<1\) با هم مقایسه کنید.
- دامنه هر دو تابع مجموعه اعداد حقیقی مثبت و برد آنها مجموعه اعداد حقیقی است.
- در حالت 1< a ، شکل نمودار تابع به صورت افزایشی و در حالت 1> a >0، شکل نمودار به صورت کاهشی است.
- هر دو تابع از نقطه (1، 0) عبور می کنند.
3
الف خط y=27 نمودار تابع \(y = {3^x}\) را در چه نقطه ای قطع می کند؟
ب خط y=10 نمودار تابع \(y = {\left( {0/01} \right)^x}\) را در چه نقطه ای قطع می کند؟
الف
\(\left\{ \begin{array}{l}y = 27\\y = {3^x}\end{array} \right. \Rightarrow {3^x} = 27 = {3^3} \Rightarrow x = 3 \Rightarrow A\left| \begin{array}{l}3\\27\end{array} \right.\)
ب
\(\begin{array}{l}\left\{ \begin{array}{l}y = 10\\y = {\left( {0/01} \right)^x}\end{array} \right. \Rightarrow {\left( {0/01} \right)^x} = 10 \Rightarrow {\left( {{{10}^{ - 2}}} \right)^x} = 10\\ \Rightarrow - 2x = 1 \Rightarrow x = - \frac{1}{2} \Rightarrow B\left| \begin{array}{l} - \frac{1}{2}\\10\end{array} \right.\end{array}\)
4 نمودار دو تابع \(g\left( x \right) = {2^x}\;,\;f\left( x \right) = {x^2}\) را رسم کنید و سپس آنها را با هم مقایسه کنید.
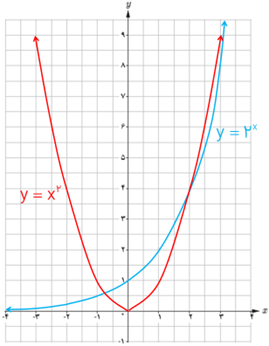
تابع \(y = {2^x}\) همواره افزایشی و یک به یک است در حالی که تابع \(y = {x^2}\) یک به یک نیست. این دو نمودار یکدیگر را در سه نقطه قطع می کنند. دو نقطه آن به طول های 4=x و 2=x و طول نقطه سوم بین دو طول 0 و 1- قرار دارد.
5 عبارت درست را با ✔ و عبارت غلط را با × علامت بزنید.
- لگاریتم اعداد مثبت کمتر از 1 همواره عددی منفی است.
- لگاریتم اعداد منفی تعریف نمی شود.
- تابع لگاریتم، تابعی یک به یک است.
- تابع لگاریتم محور yها را قطع می کند.
- اگر نقطۀ (b,d) روی نمودار \(y = {a^x}\) قرار داشته باشد، آنگاه (b,d) روی نمودار \(y = {\log _a}x\) قرار دارد.
- اگر \(a>b>0\) آنگاه \({\log _{10}}a > {\log _{10}}b\)
- لگاریتم اعداد مثبت کمتر از 1 همواره عددی منفی است. ×
- لگاریتم اعداد منفی تعریف نمی شود. ✔
- تابع لگاریتم، تابعی یک به یک است. ✔
- تابع لگاریتم محور yها را قطع می کند. ×
- اگر نقطۀ (b,d) روی نمودار \(y = {a^x}\) قرار داشته باشد، آنگاه (b,d) روی نمودار \(y = {\log _a}x\) قرار دارد. ✔
- اگر \(a>b>0\) آنگاه \({\log _{10}}a > {\log _{10}}b\) ×
6 نمودار تابع های زیر را رسم کنید.
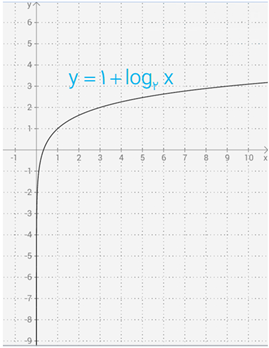
الف \(y = 1 + {\log _3}x\)
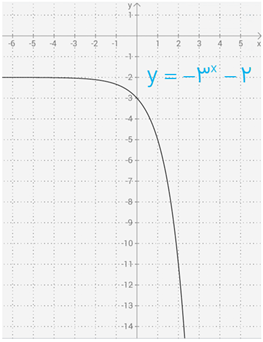
ب \(y = - {3^x} - 2\)
پ \(y = 4{\left( {\frac{1}{3}} \right)^x}\)
الف
ب
پ
گام به گام کتاب های پایه یازدهم
گام به گام جامع کتاب حسابان یازدهم
گام به گام جامع کتاب فیزیک یازدهم ریاضی
گام به گام جامع کتاب شیمی یازدهم
گام به گام جامع کتاب هندسه یازدهم
گام به گام جامع کتاب آمار و احتمال یازدهم ریاضی
گام به گام جامع کتاب زمین شناسی
گام به گام جامع کتاب فارسی یازدهم
گام به گام جامع کتاب نگارش یازدهم
گام به گام جامع کتاب عربی یازدهم
گام به گام جامع کتاب زبان انگلیسی یازدهم
گام به گام جامع کتاب کتاب کار انگلیسی یازدهم
گام به گام جامع کتاب انسان و محیط زیست
گام به گام جامع کتاب دین و زندگی یازدهم
گام به گام جامع کتاب آزمایشگاه علوم تجربی یازدهم
گام به گام جامع کتاب تاریخ معاصر ایران
کاردرکلاس صفحه 87 درس توابع نمایی و لگاریتمی حسابان یازدهم
پاسخ کاردرکلاس صفحه 87 درس 3
جواب کاردرکلاس صفحه 87 درس 3 حسابان یازدهم
1- نشان دهید که اگر a,b,c>0 و c≠1، آنگاه
\({\log _c}\frac{a}{b} = {\log _c}a - {\log _c}b\)
\(\begin{array}{l}{\log _c}\frac{a}{b} = {\log _c}\left( {a \times \frac{1}{b}} \right) = {\log _c}a + {\log _c}\frac{1}{b}\\ = {\log _c}a + {\log _c}{b^{ - 1}} = {\log _c}a - {\log _c}b\end{array}\)
2 اگر \(b = \log 3\;,\;a = \log 2\) ، حاصل عبارت های زیر را برحسب a و b بنویسید.
الف \(\log 0/75\)
ب \(3\log \sqrt[3]{4} - \log 250\)
پ \(\log 0/005\)
الف
\(\log 0/75 = \log \frac{3}{4} = \log 3 - \log 4 = \log 3 - 2\log 2 = b - 2a\)
ب
\(\begin{array}{l}3\log \sqrt[3]{4} - \log 250 = 3\log {2^{\frac{2}{3}}} - \log \frac{{1000}}{{{2^2}}}\\\\ = 3 \times \frac{2}{3}\log 2 - \left( {\log 1000 - 2\log 2} \right)\\\\ = 2a - \left( {3 - 2a} \right) = 4a - 3\end{array}\)
پ
\(\begin{array}{l}\log 0/005 = \log \frac{1}{{200}} = \log 1 - \log \left( {2 \times {{10}^2}} \right)\\\\ = 0 - \left( {\log 2 + 2\log 10} \right) = - a - 2\end{array}\)
فعالیت صفحه 88 درس توابع نمایی و لگاریتمی حسابان یازدهم
پاسخ فعالیت صفحه 88 درس 3
جواب فعالیت صفحه 88 درس 3 حسابان یازدهم
معادله های لگاریتمی زیر را حل کنید:
الف \({\log _5}\left( {2x - 1} \right) = {\log _5}x\)
ب \({\log _3}\left( {x - 1} \right) + {\log _3}\left( {\frac{x}{2} + 1} \right) = 2\)
پ \(\log x + \log \left( {x + 3} \right) = 1\)
الف
\(\begin{array}{l}\left\{ \begin{array}{l}2x - 1 > 0 \Rightarrow x > \frac{1}{2}\quad \left( i \right)\\x > 0\quad \left( {ii} \right)\end{array} \right.\quad \mathop \Rightarrow \limits^{\left( i \right),\left( {ii} \right)} \;x > \frac{1}{2}\quad \left( {iii} \right)\\{\log _5}\left( {2x - 1} \right) = {\log _5}x \Rightarrow 2x - 1 = x\;\mathop \Rightarrow \limits^{\left( {iii} \right)} \;x = 1\end{array}\)
ب
\(\begin{array}{l}\left\{ \begin{array}{l}x - 1 > 0 \Rightarrow x > 1\quad \left( i \right)\\\frac{x}{2} + 1 > 0 \Rightarrow x > - 2\quad \left( {ii} \right)\end{array} \right.\quad \mathop \Rightarrow \limits^{\left( i \right),\left( {ii} \right)} \;x > 1\quad \left( {iii} \right)\\\\{\log _3}\left( {x - 1} \right) + {\log _3}\left( {\frac{x}{2} + 1} \right) = 2\\\\ \Rightarrow {\log _3}\left\{ {\left( {x - 1} \right)\left( {\frac{x}{2} + 1} \right)} \right\} = 2\\\\ \Rightarrow \frac{1}{2}{x^2} + \frac{1}{2}x - 1 = 9 \Rightarrow {x^2} + x - 20 = 0\\\\ \Rightarrow \left( {x - 4} \right)\left( {x + 5} \right) = 0\\\\ \Rightarrow \left\{ \begin{array}{l}x = - 5\\x = 4\end{array} \right.\;\mathop \Rightarrow \limits^{\left( {iii} \right)} \;x = 4\end{array}\)
پ
\(\begin{array}{l}\left\{ \begin{array}{l}x > 0\quad \left( i \right)\\x + 3 > 0 \Rightarrow x > - 3\quad \left( {ii} \right)\end{array} \right.\quad \mathop \Rightarrow \limits^{\left( i \right),\left( {ii} \right)} \;x > 0\quad \left( {iii} \right)\\\\\log x + \log \left( {x + 3} \right) = 1 \Rightarrow \log \left\{ {x\left( {x + 3} \right)} \right\} = 1\\\\ \Rightarrow {x^2} + 3x = 10\\\\ \Rightarrow {x^2} + 3x - 10 = 0 \Rightarrow \left( {x + 5} \right)\left( {x - 2} \right) = 0\\\\ \Rightarrow \left\{ \begin{array}{l}x = - 5\\x = 2\end{array} \right.\;\mathop \Rightarrow \limits^{\left( i \right),\left( {ii} \right)} \;x = 2\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه یازدهم- آزمون آنلاین تمامی دروس پایه یازدهم
- گام به گام تمامی دروس پایه یازدهم
- ویدئو های آموزشی تمامی دروس پایه یازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه یازدهم
- فلش کارت های آماده دروس پایه یازدهم
- گنجینه ای جامع از انشاء های آماده پایه یازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه یازدهم
تمرین صفحه 90 درس توابع نمایی و لگاریتمی حسابان یازدهم
پاسخ تمرین صفحه 90 درس 3
جواب تمرین صفحه 90 درس 3 حسابان یازدهم
1 معادلات لگاریتمی زیر را حل کنید.
\({\log _4}{m^2} - {\log _4}m - 3 = 0\) الف
ب \({\log _2}\left( {12b - 21} \right) - {\log _2}\left( {{b^2} - 3} \right) = 2\)
پ \({\log _{\frac{1}{{10}}}}\left( {{x^2} - 1} \right) = - 1\)
الف
\(\begin{array}{l}{\log _4}{m^2} - {\log _4}m - 3 = 0 \Rightarrow {\log _4}\left( {\frac{{{m^2}}}{{3m}}} \right) = 0\\\\ \Rightarrow \frac{m}{3} = 1 \Rightarrow m = 1\end{array}\)
ب
\(\begin{array}{l}{\log _2}\left( {12b - 21} \right) - {\log _2}\left( {{b^2} - 3} \right) = 2 \Rightarrow {\log _2}\left\{ {\frac{{12b - 21}}{{{b^2} - 3}}} \right\} = 2\\\\ \Rightarrow \frac{{12b - 21}}{{{b^2} - 3}} = 4\\\\ \Rightarrow 4{b^2} - 12 = 12b - 21 \Rightarrow 4{b^2} - 12b + 9 = 0\\\\ \Rightarrow {\left( {2b - 3} \right)^2} = 0 \Rightarrow b = \frac{3}{2}\\\\ \Rightarrow 12b - 21 = 18 - 21 = - 3\end{array}\)
پ
\(\begin{array}{l}{\log _{\frac{1}{{10}}}}\left( {{x^2} - 1} \right) = - 1 \Rightarrow {x^2} - 1 = {\left( {\frac{1}{{10}}} \right)^{ - 1}}\\\\ \Rightarrow {x^2} - 1 = 10\\\\ \Rightarrow {x^2} = 9 \Rightarrow \left\{ \begin{array}{l}x = 3\\x = - 3\end{array} \right.\end{array}\)
2 الف در فعالیت 1 از درس اول این فصل، دیدیم که جرم باکتری ها در زمان t از فرمول \(m\left( t \right) = {2^t}\) به دست می آید. معکوس این تابع را بنویسید و آن را تفسیر کنید.
ب با استفاده از وارون تابع m(t)، برآورد کنید در چه زمانی جرم باکتری ها حدود 5000 گرم می شود؟
\(\log 2 \simeq 0/301\)
الف
\(m\left( t \right) = {2^t} \Leftrightarrow {m^{ - 1}}\left( t \right) = {\log _2}m\left( t \right) = t\)
تفسیرش این است که اگر بخواهیم بدانیم که چه میزان زمان لازم است تا (t)m گرم باکتری تولید شود، بایستی از رابطه بالا استفاده کنیم.
ب
\(\begin{array}{l}m\left( t \right) = 5000 \Rightarrow t = {\log _2}5000 = {\log _2}{5^4} \times {2^3}\\\\ = 4{\log _2}5 + 3{\log _2}2 = 4{\log _2}\frac{{10}}{2} + 3\end{array}\)
\( = 4\left( {{{\log }_2}10 - {{\log }_2}2} \right) + 3\)
ساعت \( = 4{\log _2}10 - 1 = 4 \times \frac{1}{{{{\log }_{10}}2}} - 1 \simeq \frac{4}{{0/301}} - 1 \simeq 12/5 \equiv 12:30'\)
3 درستی یا نادرستی عبارت های زیر را بررسی کنید:
الف \(\left( {b \ne 1\;,\;a\;,\;b > 0} \right)\;\;\;{a^{{{\log }_b}a}} = 0\)
ب \(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\left( {d \ne 1\;,\;a\;,\;b\;,\;c\;,\;d > 0} \right)\;\;\;{\log _d}abc = {\log _d}a + {\log _d}b + {\log _d}c\)
پ \(\log x\;\log y = \log x + \log y\)
ت لگاریتم هر عدد مثبت، همواره عددی مثبت است.
الف
\(\left( {b \ne 1\;,\;a\;,\;b > 0} \right)\;\;\;{a^{{{\log }_b}a}} = 0\) ×
\(\begin{array}{l}{a^{{{\log }_b}a}} = a\mathop \Rightarrow \limits^{\left( {{{\log }_b}} \right)} {\log _b}\left( {{a^{{{\log }_b}a}}} \right) = {\log _b}a \Rightarrow {\log _b}a \times {\log _b}a = {\log _b}a\\\\ \Rightarrow {\log _b}a = 1 \Rightarrow a = b \times \end{array}\)
ب
\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\left( {d \ne 1\;,\;a\;,\;b\;,\;c\;,\;d > 0} \right)\;\;\;{\log _d}abc = {\log _d}a + {\log _d}b + {\log _d}c\) ✔
\(\begin{array}{l}{\log _d}abc = {\log _d}a\left( {bc} \right) = {\log _d}a + {\log _d}bc\\\\ = {\log _d}a + {\log _d}b + {\log _d}c\end{array}\)
پ
\(\log x\;\log y = \log x + \log y\) ×
\(\begin{array}{l}\log x\;\log y = \log x + \log y\\\\ \Rightarrow \log {x^{\log y}} = \log xy \Rightarrow xy = {x^{\log y}} \times \end{array}\)
ت
لگاریتم هر عدد مثبت، همواره عددی مثبت است. ×
\(\log \left( {0/1} \right) = \log {10^{ - 1}} = - \log 10 = - 1\)
4 نیمه عمر عنصری چهار روز و جرم اولیه یک نمونه از آن یک گرم است.
الف جرم m(t) را که پس از t روز باقی می ماند، بیابید.
ب طی چند روز، این جرم به 0/01 گرم کاهش می یابد؟
الف
\(m\left( t \right) = 1 \times {2^{ - \;\frac{t}{4}}} = {2^{ - \;\frac{t}{4}}}\)
ب
\(\begin{array}{l}\left\{ \begin{array}{l}m\left( t \right) = {2^{ - \;\frac{t}{4}}}\\m\left( t \right) = 0/01\end{array} \right. \Rightarrow 0/01 = {2^{ - \;\frac{t}{4}}}\\\\ \Rightarrow \log {10^{ - 2}} = \log {2^{ - \;\frac{t}{4}}} = - \;\frac{t}{4}\log 2\\\\ \Rightarrow - 2 = - \;\frac{t}{4}\log 2\end{array}\)
روز \( \Rightarrow t = \frac{8}{{\log 2}} \simeq \frac{8}{{0/301}} \simeq 26/5\)
5 عبارات زیر را ساده کنید. \(\left( {\log 3 = 0/4771\;\;,\;\;\log 2 = 0/301} \right)\)
الف \(\log \left( {18 \times 375} \right)\)
ب \(\log \sqrt {0/75} \)
پ \({\log _2}\frac{{\sqrt 8 }}{{\sqrt[4]{2}}}\)
الف
\(\begin{array}{l}\log \left( {18 \times 375} \right) = \log \left( {2 \times {3^2} \times 3 \times {5^3}} \right)\\\\ = \log \left( {2 \times {3^3} \times {{\left( {\frac{{10}}{2}} \right)}^3}} \right) = \log \left( {{2^{ - 2}} \times {3^3} \times {{10}^3}} \right)\\\\ = - 2\log 2 + 3\log 3 + 3\log 10\\\\ \simeq - 2 \times 0/301 + 3 \times 0/4771 + 3 = 3/8293\end{array}\)
ب
\(\begin{array}{l}\log \sqrt {0/75} = \frac{1}{2}\log \frac{3}{4} = \frac{1}{2}\left( {\log 3 - \log {2^2}} \right) = \frac{1}{2}\left( {\log 3 - 2\log 2} \right)\\\\ = \frac{1}{2}\left( {0/4771 - 2 \times 0/301} \right)\\\\ = - 0/06245\end{array}\)
پ
\(\begin{array}{l}{\log _2}\frac{{\sqrt 8 }}{{\sqrt[4]{2}}} = {\log _2}\sqrt {{2^3}} - {\log _2}\sqrt[4]{2} = {\log _2}{2^{\frac{3}{2}}} - {\log _2}{2^{\frac{1}{4}}}\\\\ = \frac{3}{2}{\log _2}2 - \frac{1}{4}{\log _2}2\\\\ = \frac{3}{2} - \frac{1}{4} = \frac{5}{4}\end{array}\)
6 اگر نمودار تابع با ضابطهٔ \(f\left( x \right) = {\log _a}x\) از نقطۀ \((\frac{1}{2}\;,\; - 4)\) عبور کند، مقدار a چند است؟
\(\begin{array}{l}\left. \begin{array}{l}f(x) = {\log _a}x\\(\frac{1}{2}\;,\;4)\end{array} \right\} \Rightarrow f(\frac{1}{2}) = 4 \Rightarrow 4 = {\log _a}\frac{1}{2}\\\\ \Rightarrow {a^4} = \frac{1}{2}\,\,\,\,\,\,\mathop \Rightarrow \limits^{a > 0\atop a \ne 1} \,\,\,\,\,a = \sqrt[4]{{\frac{1}{2}}} = \frac{1}{{\sqrt[4]{2}}} = \frac{{\sqrt[4]{8}}}{2}\end{array}\)
7 گزینه های درست را با ✔ و گزینه های نادرست را با × علامت بزنید.
\(\begin{array}{l}{\log _b}a \times {\log _a}b = 1\\\\\log \;5 = \log \;3 + \log \;2\end{array}\)
\({\log _b}a \times {\log _a}b = 1\) ✔
\(\begin{array}{l}{b^{{{\log }_b}a \times {{\log }_a}b}} = {b^1} = b \Rightarrow \\{({b^{{{\log }_b}a}})^{{{\log }_a}b}} = {a^{{{\log }_a}b}} = b\end{array}\)
\(\log \;5 = \log \;3 + \log \;2\) ×
\(\begin{array}{l}\log 5 = \log (3 \times 2) = \log 6\\ \Rightarrow 5 = 6\mathop {}\nolimits^{} \times \end{array}\)
8 نیمه عمر یک ماده هسته ای 30 سال است. نمونه ای از این ماده 128 میلی گرم جرم دارد. جرمی که پس از 300 سال باقی می ماند چقدر است؟
\(\begin{array}{l}m\left( t \right) = 128 \times {2^{ - \;\frac{t}{{30}}}} \Rightarrow m\left( {300} \right) = 128 \times {2^{ - \;\frac{{300}}{{30}}}}\\\\ = {2^7} \times {2^{ - 10}} = {2^{ - \,3}} = 0/125\end{array}\)



1736019749.png)















