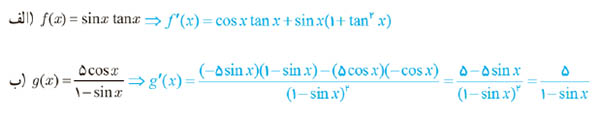جواب فصل 4 مشتق حسابان دوازدهم
تعداد بازدید : 3.13Mپاسخ به تمامی سوالات فصل مشتق - حل المسائل فصل 4 مشتق - گام به گام 1401 کتاب حسابان دوازدهم - گام به گام کتاب حسابان دوازدهم مطابق با آخرین تغییرات کتب درسی
فعالیت صفحه 72 درس مشتق حسابان دوازدهم
پاسخ فعالیت صفحه 72 درس 4
جواب فعالیت صفحه 72 درس 4 حسابان دوازدهم
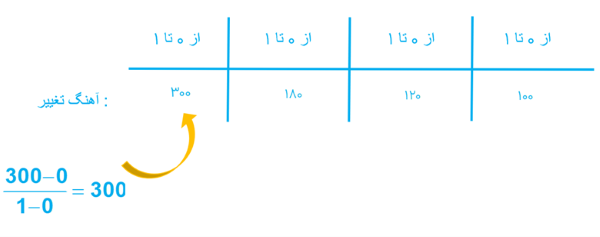
1 شیب هر یک از خط های داده شده را مشخص کنید.
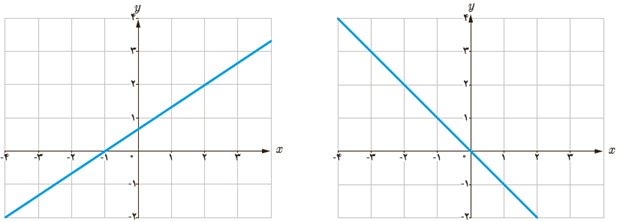
\(\begin{array}{l}A = \left| \begin{array}{l} - 1\\\\0\end{array} \right.\,\,\,\,\,,\,\,\,\,\,B = \left| \begin{array}{l}2\\\\2\end{array} \right.\\\\{m_{AB}} = \frac{{2 - 0}}{{2 - ( - 1)}} = \frac{2}{3}\\\\ \Rightarrow {m_{AB}} > 0\end{array}\)
\(\begin{array}{l}A = \left| \begin{array}{l} - 2\\\\2\end{array} \right.\,\,\,\,\,,\,\,\,\,\,B = \left| \begin{array}{l}0\\\\0\end{array} \right.\\\\{m_{AB}} = \frac{{0 - 2}}{{0 - ( - 2)}} = \frac{{ - 2}}{2} = - 1\\\\ \Rightarrow {m_{AB}} < 0\end{array}\)
2 با توجه به جدول روبه رو، نمودار مربوط به خط های d1 ، d2 ، d3 و d4 را روی شکل مشخص کنید.
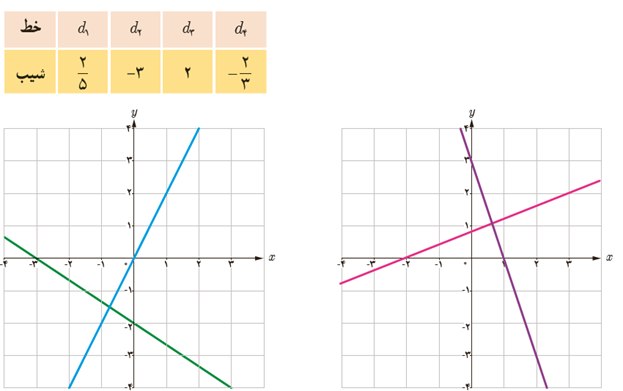
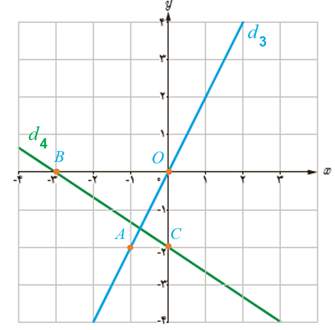
\(\begin{array}{l}A\left| {\begin{array}{*{20}{c}}{ - 1}\\{ - 2}\end{array}} \right.\;,\;O\left| {\begin{array}{*{20}{c}}0\\0\end{array}} \right. \Rightarrow m = \frac{{0 - ( - 2)}}{{0 - ( - 1)}} = 2 = {m_{{d_3}}}\\B\left| {\begin{array}{*{20}{c}}{ - 3}\\0\end{array}} \right.\;,\;C\left| {\begin{array}{*{20}{c}}0\\{ - 2}\end{array}} \right. \Rightarrow m = \frac{{ - 2 - 0}}{{0 - ( - 3)}} = - \frac{2}{3} = {m_{{d_4}}}\end{array}\)

\(\begin{array}{l}D\left| {\begin{array}{*{20}{c}}{ - 2}\\0\end{array}} \right.\;,\;E\left| {\begin{array}{*{20}{c}}3\\2\end{array}} \right. \Rightarrow m = \frac{{3 - ( - 2)}}{{2 - 0}} = \frac{5}{2} = {m_{{d_1}}}\\F\left| {\begin{array}{*{20}{c}}0\\3\end{array}} \right.\;,\;G\left| {\begin{array}{*{20}{c}}1\\0\end{array}} \right. \Rightarrow m = \frac{{0 - 3}}{{1 - 0}} = - 3 = {m_{{d_2}}}\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دوازدهم- آزمون آنلاین تمامی دروس پایه دوازدهم
- گام به گام تمامی دروس پایه دوازدهم
- ویدئو های آموزشی تمامی دروس پایه دوازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دوازدهم
- فلش کارت های آماده دروس پایه دوازدهم
- گنجینه ای جامع از انشاء های آماده پایه دوازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دوازدهم
فعالیت صفحه 74 درس مشتق حسابان دوازدهم
پاسخ فعالیت صفحه 74 درس 4
جواب فعالیت صفحه 74 درس 4 حسابان دوازدهم
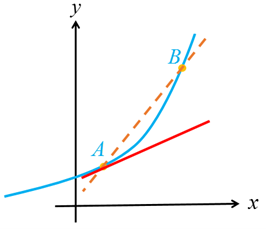
اکنون سعی می کنیم که به کمک نمودار منحنی، خط مماس بر منحنی در یک نقطه را بررسی کنیم. نقطه ثابت A را روی منحنی زیر در نظر می گیریم. خطی که از A و B می گذرد یک خط قاطع نامیده می شود. روی منحنی نقطه های دیگری را نزدیک تر به نقطه A اختیار می کنیم و خط های گذرنده از A و آن نقطه ها را رسم می کنیم. حدس بزنید که وقتی نقاط به قدر کافی به A نزدیک می شوند، برای خط های قاطع چه اتفاقی می افتد؟ به عبارت دیگر خط های قاطع به چه خطی نزدیک می شوند؟
خط مماس
اکنون نقطه C را سمت چپ نقطه A اختیار می کنیم و خط قاطع AC را رسم می کنیم. مانند قبل نقاط دیگری را نزدیک تر به نقطه A اختیار می کنیم. حدس می زنید برای خط های قاطع چه اتفاقی می افتد؟
به طور شهودی می توان گفت:
شیب خط مماس بر منحنی در نقطه A حد شیب خط های قاطع گذرنده از A است به شرطی که نقطه ها به قدر کافی به A نزدیک شوند.
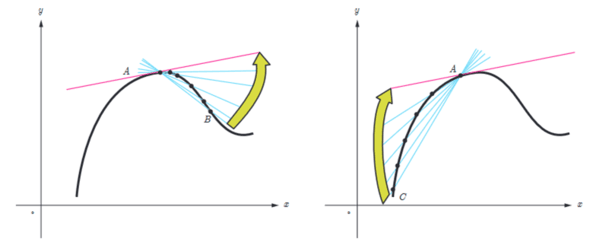
به خط مماس نزدیک می شوند.
گام به گام کتاب های پایه دوازدهم
گام به گام جامع کتاب حسابان دوازدهم
گام به گام جامع کتاب فیزیک دوازدهم ریاضی
گام به گام جامع کتاب شیمی دوازدهم
گام به گام جامع کتاب هندسه دوازدهم
گام به گام جامع کتاب ریاضیات گسسته
گام به گام جامع کتاب فارسی دوازدهم
گام به گام جامع کتاب نگارش دوازدهم
گام به گام جامع کتاب عربی دوازدهم
گام به گام جامع کتاب زبان انگلیسی دوازدهم
گام به گام جامع کتاب کتاب کار انگلیسی دوازدهم
گام به گام جامع کتاب دین و زندگی دوازدهم
گام به گام جامع کتاب هویت اجتماعی
گام به گام جامع کتاب سلامت و بهداشت
گام به گام جامع کتاب مدیریت خانواده و سبک زندگی (پسران)
فعالیت صفحه 74 درس مشتق حسابان دوازدهم
پاسخ فعالیت صفحه 74 درس 4
جواب فعالیت صفحه 74 درس 4 حسابان دوازدهم
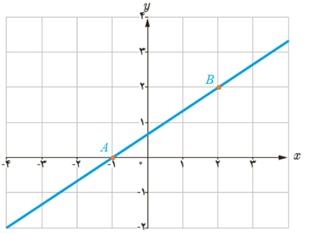
الف تابع \(f\left( x \right) = - {x^2} + 10x\) داده شده است، اگر \(0 \le x \le 10\) نقاط \(A(2,f(2))\), \(B(6,f(6))\), \(C(5,f(5)) \), \(D(4,f(4))\) و \(E(3,f(3)) \) را روی منحنی در نظر می گیریم. شیب خطی که از نقاط A و B می گذرد یعنی mAB از دستور زیر به دست می آید:
\({m_{AB}} = \frac{{{v_B} - {v_A}}}{{{x_B} - {x_A}}} = \frac{{f\left( 6 \right) - f\left( 2 \right)}}{{6 - 2}} = \frac{{24 - 16}}{4} = \frac{8}{4} = 2\)
به همین روش mAC و mAD و mAE را به دست آورید.
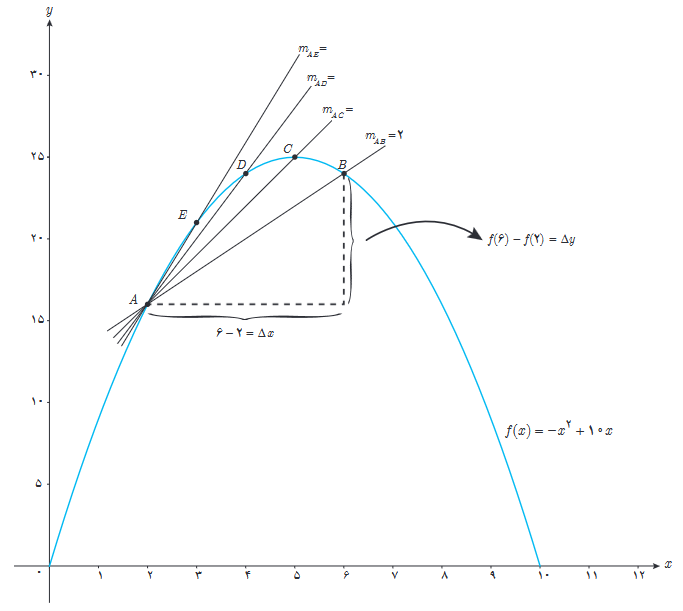
\(\begin{array}{l}A\left| {\begin{array}{*{20}{c}}2\\{16}\end{array}\quad ,\quad } \right.B\left| {\begin{array}{*{20}{c}}6\\{24}\end{array}\quad ,\quad } \right.C\left| {\begin{array}{*{20}{c}}5\\{25}\end{array}\quad ,\quad D} \right.\left| {\begin{array}{*{20}{c}}4\\{24}\end{array}\quad ,\quad E} \right.\left| {\begin{array}{*{20}{c}}3\\{21}\end{array}} \right.\\{m_{AC}} = \frac{{{y_C} - {y_A}}}{{{x_C} - {x_A}}} = \frac{{25 - 16}}{{5 - 2}} = \frac{9}{3} = 3\\{m_{AD}} = \frac{{{y_D} - {y_A}}}{{{x_D} - {x_A}}} = \frac{{24 - 16}}{{4 - 2}} = \frac{8}{2} = 4\\{m_{AE}} = \frac{{{y_E} - {y_A}}}{{{x_E} - {x_A}}} = \frac{{21 - 16}}{{3 - 2}} = \frac{5}{1} = 5\end{array}\)
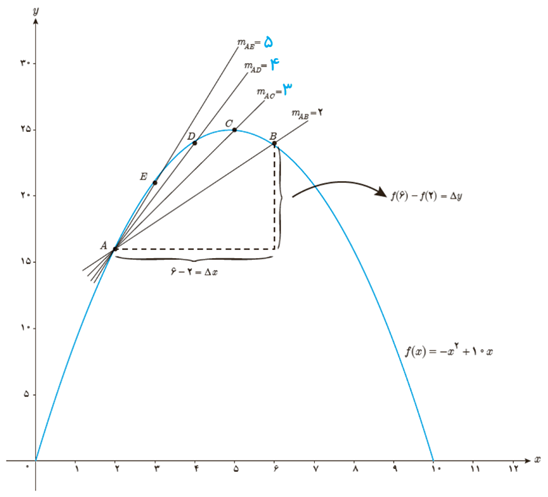
همان طور که می دانید برای محاسبه شیب خط AB نسبت تغییر عمودی را به تغییر افقی به دست می آوریم. اگر این تغییرات را به ترتیب با Δy و Δx نمایش دهیم، داریم:
\({m_{AB}} = \frac{{\Delta y}}{{\Delta x}}\)
در هنگام محاسبه شیب های بالا، توضیح دهید که Δxها چگونه تغییر می کنند؟
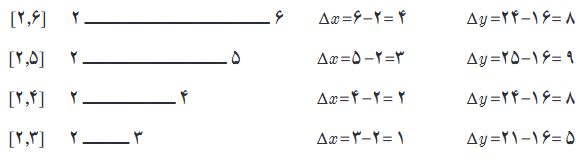
مقدارشان کوچکتر می شود.
ب حال فرض کنید که با ادامه روندی که در قسمت (الف) اختیار کردیم، نقاط بیشتری را نزدیک به A انتخاب کنیم. شیب خطوط به دست آمده به شیب خط مماس بر منحنی در نقطه A نزدیک می شود. برای درک بهتر این موضوع، منحنی \(f\left( x \right) = - {x^2} + 10x\) در فاصله [2,3] رسم شده است. در ادامه نمودار تابع در بازه [2,2/4] رسم شده است.
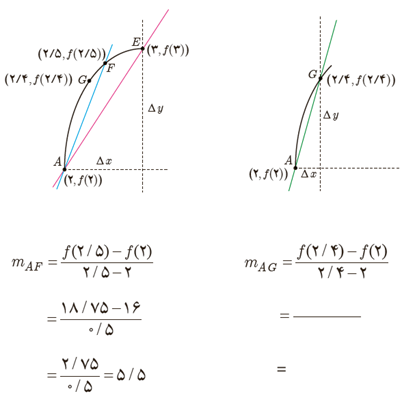
\(\begin{array}{l}{m_{AG}} = \frac{{f(2/4) - f(2)}}{{2/4 - 2}}\\\\ = \frac{{18/25 - 16}}{{2/4 - 2}} = \frac{{2/25}}{{0/4}}\\\\ = 5/625\end{array}\)
اگر به همین ترتیب بازه های کوچک تری در نظر بگیریم، شیب خطوط به دست آمده به شیب خط مماس بر منحنی در نقطه A نزدیک می شود. برای درک بهتر این موضوع، با تکمیل جدول و مقایسه شیب خط های قاطع، شیب خط مماس را حدس بزنید.


مقدارهای بدست آمده به عدد 6 نزدیک می شوند.
کار در کلاس صفحه 78 درس مشتق حسابان دوازدهم
پاسخ کار در کلاس صفحه 78 درس 4
جواب کار در کلاس صفحه 78 درس 4 حسابان دوازدهم
معادله خط مماس بر منحنی تابع y=x2+3 را در نقطه ای به طول 2- بنویسید.
\(\begin{array}{l}f( - 2) = {( - 2)^2} + 3 = 7\\\\f( - 2 + h) = {( - 2 + h)^2} + 3\\\\ = 4 - 4h + {h^2} + 3 = {h^2} - 4h + 7\\\\ \Rightarrow f'( - 2) = \mathop {\lim }\limits_{h \to \:0} \frac{{f( - 2 + h) - f( - 2)}}{h}\\\\ = \mathop {\lim }\limits_{h \to \:0} \frac{{h(h - 4)}}{h} = \mathop {\lim }\limits_{h \to \:0} (h - 4) = - 4\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دوازدهم- آزمون آنلاین تمامی دروس پایه دوازدهم
- گام به گام تمامی دروس پایه دوازدهم
- ویدئو های آموزشی تمامی دروس پایه دوازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دوازدهم
- فلش کارت های آماده دروس پایه دوازدهم
- گنجینه ای جامع از انشاء های آماده پایه دوازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دوازدهم
کار در کلاس صفحه 80 درس مشتق حسابان دوازدهم
پاسخ کار در کلاس صفحه 80 درس 4
جواب کار در کلاس صفحه 80 درس 4 حسابان دوازدهم
اگر f’(a) موجود باشد، ثابت کنید.
\(\mathop {\lim }\limits_{h \to 0} \frac{{f\left( {a + h} \right) - f\left( a \right)}}{h} = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( x \right) - f\left( a \right)}}{{x - a}}\)
راهنمایی: تغییر متغیر a + h = x را به کار برید. توجه کنید وقتی که \( h\to 0\) آنگاه \(x \to a \)
اگر قرار دهیم \(a + h = x\) نتیجه می گیریم که\(h = x - a\) . حال اگر\(h \to 0\) پس\(x - a \to 0\) ، یعنی \(x \to a\)؛ لذا :
\(\mathop {\lim }\limits_{h \to \;0} \frac{{f(a + h) - f(a)}}{{x - a}} = \mathop {\lim }\limits_{x \to \;a} \frac{{f(x) - f(a)}}{{x - a}}\)
گام به گام کتاب های پایه دوازدهم
گام به گام جامع کتاب حسابان دوازدهم
گام به گام جامع کتاب فیزیک دوازدهم ریاضی
گام به گام جامع کتاب شیمی دوازدهم
گام به گام جامع کتاب هندسه دوازدهم
گام به گام جامع کتاب ریاضیات گسسته
گام به گام جامع کتاب فارسی دوازدهم
گام به گام جامع کتاب نگارش دوازدهم
گام به گام جامع کتاب عربی دوازدهم
گام به گام جامع کتاب زبان انگلیسی دوازدهم
گام به گام جامع کتاب کتاب کار انگلیسی دوازدهم
گام به گام جامع کتاب دین و زندگی دوازدهم
گام به گام جامع کتاب هویت اجتماعی
گام به گام جامع کتاب سلامت و بهداشت
گام به گام جامع کتاب مدیریت خانواده و سبک زندگی (پسران)
کار در کلاس صفحه 80 درس مشتق حسابان دوازدهم
پاسخ کار در کلاس صفحه 80 درس 4
جواب کار در کلاس صفحه 80 درس 4 حسابان دوازدهم
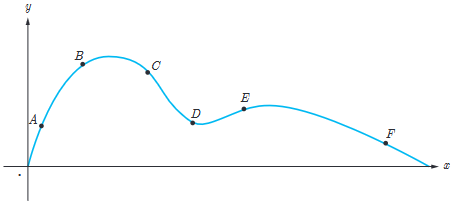
الف برای تابع \(f(x)=-x2+10x \), f’(8) و f’(5) را حساب کنید.
ب دو نقطه روی منحنی مشخص کنید که مقدار مشتق تابع در آنها قرینه یکدیگر باشد.
پ به کمک شکل توضیح دهید که تابع در چه نقاطی دارای مشتق مثبت و در چه نقاطی مشتق منفی است.
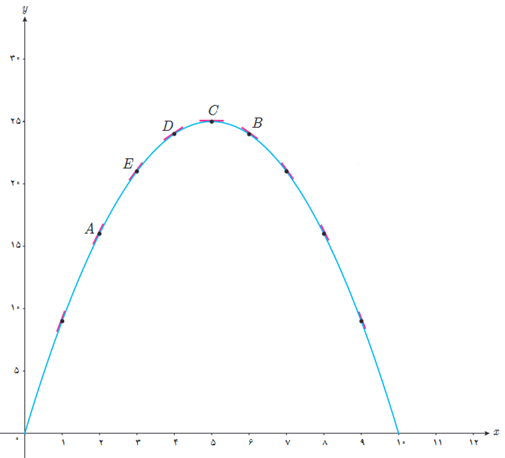
ت بدون محاسبه و تنها به کمک نمودار، شیب خط های مماس بر منحنی در نقاط 3 و 4 را با هم مقایسه کنید.
ث با محاسبه f’(3) و f’(4) صحت حدس خود را بررسی نمایید.
الف
\(\begin{array}{l}f(8) = - {(8)^2} + 10(8) = 16\\ \Rightarrow f'(8) = \mathop {\lim }\limits_{x \to 8} \frac{{f(x) - f(8)}}{{x - 8}} = \mathop {\lim }\limits_{x \to 8} \frac{{ - {x^2} + 10x - 16}}{{x - 8}} = \mathop {\lim }\limits_{x \to 8} \frac{{ - (x - 2)(x - 8)}}{{x - 8}} = - 6\\\\f(5) = - {(5)^2} + 10(5) = 25\\ \Rightarrow f'(5) = \mathop {\lim }\limits_{x \to 5} \frac{{f(x) - f(5)}}{{x - 5}} = \mathop {\lim }\limits_{x \to 5} \frac{{ - {x^2} + 10x - 25}}{{x - 5}} = \mathop {\lim }\limits_{x \to 5} \frac{{ - {{(x - 5)}^2}}}{{x - 5}} = \mathop {\lim }\limits_{x \to 5} - (x - 5) = 0\end{array}\)
ب
A و F
پ
در نقاط A و E و D، شیب مثبت و در نقاط B و G و F شیب منفی است.
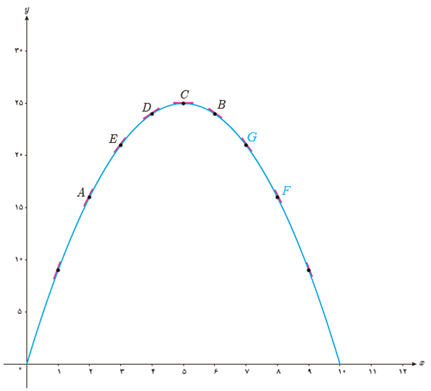
ت
\(f'(3) > f'(4)\) و \({m_E} > {m_D}\)
ث
\(\begin{array}{l}f(3) = - {(3)^2} + 10(3) = 21\\ \Rightarrow f'(3) = \mathop {\lim }\limits_{x \to 3} \frac{{f(x) - f(3)}}{{x - 3}} = \mathop {\lim }\limits_{x \to 3} \frac{{ - {x^2} + 10x - 21}}{{x - 3}} = \mathop {\lim }\limits_{x \to 3} \frac{{ - (x - 7)(x - 3)}}{{x - 3}} = 4\\\\f(4) = - {(4)^2} + 10(4) = 24\\ \Rightarrow f'(4) = \mathop {\lim }\limits_{x \to 4} \frac{{f(x) - f(4)}}{{x - 4}} = \mathop {\lim }\limits_{x \to 4} \frac{{ - {x^2} + 10x - 24}}{{x - 4}} = \mathop {\lim }\limits_{x \to 4} \frac{{ - (x - 6)(x - 4)}}{{x - 4}} = \mathop {\lim }\limits_{x \to 4} - (x - 6) = 2\end{array}\)
لذا \(f'(3) > f'(4)\)
تمرین صفحه 81 درس مشتق حسابان دوازدهم
پاسخ تمرین صفحه 81 درس 4
جواب تمرین صفحه 81 درس 4 حسابان دوازدهم
1 اگر \(f\left( x \right) = 3{x^2} - 2x + 1\) ، f’(2) را به دست آورید و معادله خط مماس بر منحنی f را در نقطه ای به طول 2 واقع بر آن بنویسید.
\(\begin{array}{l}f'(2) = \mathop {\lim }\limits_{x \to 2} \frac{{f(x) - f(2)}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{3{x^2} + 2x + 1 - 9}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{3{x^2} + 2x - 8}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{(x - 2)(3x + 4)}}{{x - 2}}\\\quad \quad \;{\kern 1pt} = \mathop {\lim }\limits_{x \to 2} (3x + 4) = 10\\ \Rightarrow y - 9 = 10(x - 2)\\ \Rightarrow y - 9 = 10x - 20\quad \Rightarrow \quad y = 10x - 11\end{array}\)
معادله خط مماس: \(y = 10x - 11\)
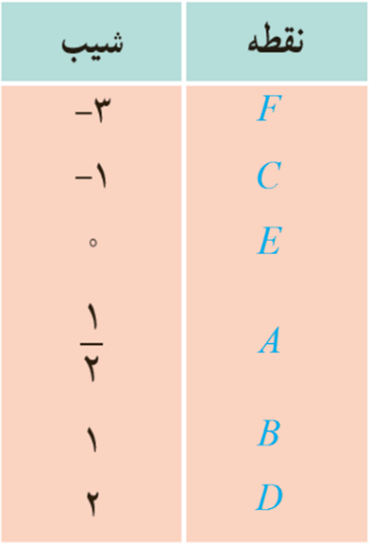
2 نقاط داده شده روی منحنی زیر را با شیب های ارائه شده در جدول نظیر کنید.
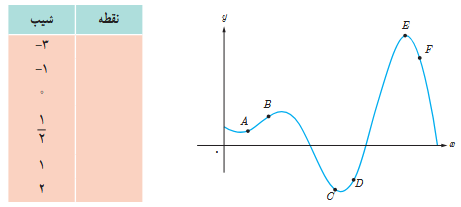
3 برای نمودار y=f(x) در شکل زیر شیب های داده شده از «الف» تا «ج» را از کوچک ترین به بزرگ ترین مرتب کنید.
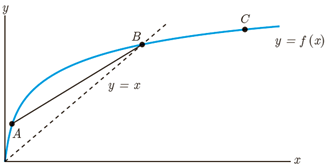
الف شیب نمودار در نقطه A
ب شیب نمودار در نقطه B
پ شیب نمودار در نقطه C
ت شیب خط AB
ث شیب خط y=2
ج شیب خط y=x
شیب های داده شده از «الف» تا «ج« را به ترتیب m2 ، m1 ، ... و m6 در نظر بگیرید.
الف
\({m_1}\)
ب
\({m_2}\)
پ
\({m_3}\)
ت
\({m_4}\)
ث
\({m_5} = 0\)
ج
\({m_6} = 1\)
\({m_5} < {m_2} < {m_3} < {m_4} < {m_6} < {m_1}\)
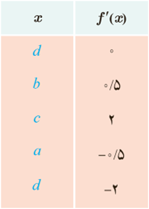
4 با در نظر گرفتن نمودار f در شکل، نقاط به طول های d، c، b، a و e را با مشتق های داده شده در جدول نظیر کنید.

5 نقاطی مانند F، E، D، C، B، A و G را روی نمودار y=f(x) مشخص کنید به طوری که:
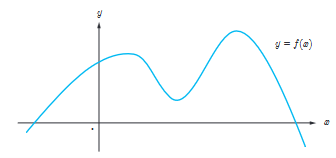
الف A ، نقطه ای روی نمودار است که شیب خط مماس بر نمودار در آن منفی است.
ب B نقطه ای روی نمودار تابع است که مقدار تابع و مقدار مشتق در آن منفی است.
پ C نقطه ای روی نمودار است که مقدار تابع در آنجا صفر است ولی مقدار مشتق در آن مثبت است.
ت D نقطه ای روی منحنی است که مشتق در آنجا صفر است.
ث نقاط E و F نقاط متفاوتی روی منحنی هستند که مشتق یکسان دارند.
ج G نقطه ای روی منحنی است که مقدار تابع در آنجا مثبت ولی مقدار مشتق منفی است.
6- اگر \(f'\left( { - 1} \right)\;,\;f\left( x \right) = {x^2} - 2\) را به دست آورید.
\(\begin{array}{l}f( - 1) = {( - 1)^3} - 2 = - 3\\ \Rightarrow f'( - 1) = \mathop {\lim }\limits_{x \to \; - 1} \frac{{f(x) - f( - 1)}}{{x + 1}} = \mathop {\lim }\limits_{x \to \; - 1} \frac{{{x^3} - 2 + 3}}{{x + 1}} = \mathop {\lim }\limits_{x \to \; - 1} \frac{{{x^3} + 1}}{{x + 1}} = \mathop {\lim }\limits_{x \to \; - 1} \frac{{(x + 1)({x^2} - x + 1)}}{{x + 1}}\\\begin{array}{*{20}{c}}{}&{}&{}\end{array}\;\;\;{\kern 1pt} {\kern 1pt} = \mathop {\lim }\limits_{x \to \; - 1} ({x^2} - x + 1) = 3\end{array}\)
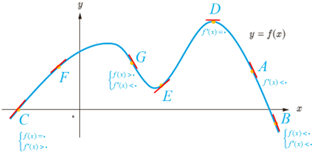
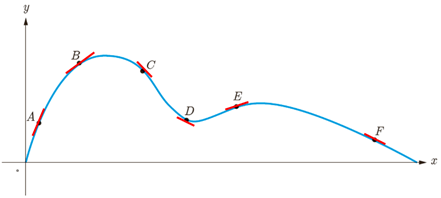
7 نقاط E، D، C، B، A و F را روی منحنی روبه رو در نظر می گیریم. در مورد شیب منحنی در این نقاط کدام گزاره درست و کدام یک نادرست است؟
الف شیب منحنی در همه این نقاط مثبت است.
ب \({m_A} < {m_B}\) (شیب خط مماس بر منحنی در نقطه A را با mA نمایش داده ایم)
پ \({m_E} < {m_B} < {m_A}\)
ت شیب منحنی در نقاط F، D و C منفی است.
ث \({m_F} < {m_D} < {m_C}\)
ج \({m_C} < {m_D} < {m_F} < {m_E} < {m_B} < {m_A}\)
الف)
نادرست؛ مثلاً در نقطه شیب منفی است.
ب)
نادرست.
پ)
درست.
ت)
درست.
ث)
نادرست؛
ج)
نادرست.
الف
نادرست؛ مثلاً در نقطه F شیب منفی است.
ب
نادرست.
پ
درست.
ت
درست.
ث
نادرست؛ \({m_C} < {m_D} < {m_F}\)
ج
نادرست.
8 برای تابع f در شکل زیر داریم: f’(4)=1/5 و f(4)=25 با توجه به شکل مختصات نقاط B، A و C را بیابید.
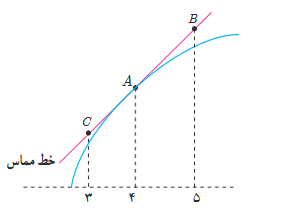
نقطه A که بر روی نمودار قرار دارد؛ پس مختصات آن معلوم است : \(A\left| {\begin{array}{*{20}{c}}4\\{25}\end{array}} \right.\)
حال نقاط B و C بر روی خطی قرار دارند که در نقطه A بر نمودار مماس هستند؛ پس بایستی ابتدا معادله خط مماس بر نمودار در نقطه A را بدست می آوریم و از آنجا مختصات باقی نقاط را محاسبه می کنیم:
\(\begin{array}{l}m = f'(4) = 1/5\\y - {y_A} = m(x - {x_A}) \Rightarrow y - 25 = 1/5(x - 4) \Rightarrow y = 1/5x + 19\\ \Rightarrow \left\{ \begin{array}{l}{x_B} = 5 \Rightarrow {y_B} = 26/5 \Rightarrow \quad B\left| {\begin{array}{*{20}{c}}5\\{26/5}\end{array}} \right.\\{x_C} = 3 \Rightarrow {y_C} = 23/5 \Rightarrow \quad C\left| {\begin{array}{*{20}{c}}3\\{23/5}\end{array}} \right.\end{array} \right.\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دوازدهم- آزمون آنلاین تمامی دروس پایه دوازدهم
- گام به گام تمامی دروس پایه دوازدهم
- ویدئو های آموزشی تمامی دروس پایه دوازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دوازدهم
- فلش کارت های آماده دروس پایه دوازدهم
- گنجینه ای جامع از انشاء های آماده پایه دوازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دوازدهم
فعالیت صفحه 84 درس مشتق حسابان دوازدهم
پاسخ فعالیت صفحه 84 درس 4
جواب فعالیت صفحه 84 درس 4 حسابان دوازدهم
نمودار تابع \(f\left( x \right) = \left\{ \begin{array}{l}{x^2}\;\;\;\;\;x \ne 2\\1\;\;\;\;\;\;\;x = 2\end{array} \right.\) (شکل مقابل) را درنظر می گیریم:
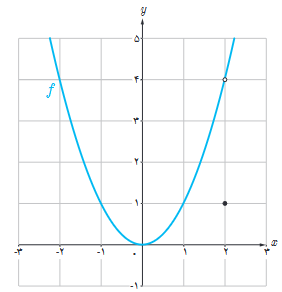
الف چگونه به کمک نمودار تابع و تعریف مشتق به عنوان شیب خط مماس می توانید استدلال کنید که f’(2) وجود ندارد؟
اگر برای بررسی مشتق پذیری این تابع در x=2 تعریف مشتق f در x=2 را به کار گیریم:
\(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{f\left( x \right) - f\left( 2 \right)}}{{x - 2}} = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{{x^2} - 1}}{{x - 2}} = \)
حد صورت کسر برابر 3 است و حد مخرج کسر برابر صفر است. وقتی \(x \to 2\) ، داریم:
\(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{{x^2} - 1}}{{x - 2}} = + \infty \)=حد راست
\(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{{x^2} - 1}}{{x - 2}} = + \infty \) =حد چپ
بنابراین \(\mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - f\left( 2 \right)}}{{x - 2}}\) موجود (و متناهی) نیست، پس f’(2) وجود ندارد.
ب نقطه دیگری (به جز x=2) در نظر بگیرید. آیا تابع در این نقطه مشتق پذیر است؟ پاسخ خود را با پاسخ دوستانتان مقایسه کنید.
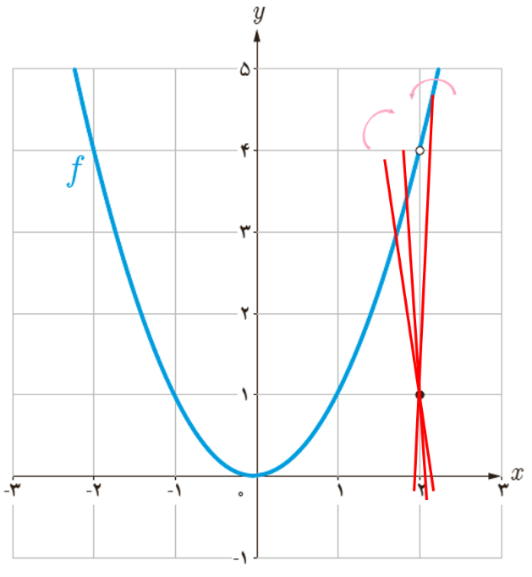
الف
شیب خط های قاطع که از نقطۀ \(x = 2\) می گذرند، به عدد حقیقی و منحصر بفردی میل نمی کنند:
ب
بله؛ هر نقطه ای که طول آن به غیر از x=2 باشد، تابع در آن مشتق پذیر خواهد بود.
گام به گام کتاب های پایه دوازدهم
گام به گام جامع کتاب حسابان دوازدهم
گام به گام جامع کتاب فیزیک دوازدهم ریاضی
گام به گام جامع کتاب شیمی دوازدهم
گام به گام جامع کتاب هندسه دوازدهم
گام به گام جامع کتاب ریاضیات گسسته
گام به گام جامع کتاب فارسی دوازدهم
گام به گام جامع کتاب نگارش دوازدهم
گام به گام جامع کتاب عربی دوازدهم
گام به گام جامع کتاب زبان انگلیسی دوازدهم
گام به گام جامع کتاب کتاب کار انگلیسی دوازدهم
گام به گام جامع کتاب دین و زندگی دوازدهم
گام به گام جامع کتاب هویت اجتماعی
گام به گام جامع کتاب سلامت و بهداشت
گام به گام جامع کتاب مدیریت خانواده و سبک زندگی (پسران)
کار در کلاس صفحه 85 درس مشتق حسابان دوازدهم
پاسخ کار در کلاس صفحه 85 درس 4
جواب کار در کلاس صفحه 85 درس 4 حسابان دوازدهم
تابع g (شکل زیر) را به صورت \(g\left( x \right) = \left\{ \begin{array}{l}{x^2}\;\;\;\;\;\;x \le 1\\x + 1\;\;\;\;x > 1\end{array} \right.\) درنظر می گیریم.
چرا g’(1) موجود نیست؟
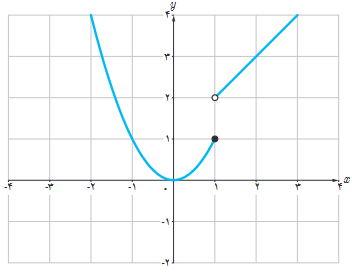
زیرا شیب خط های قاطع که از نقطۀ x=1 می گذرند، به عدد حقیقی و منحصر بفردی میل نمی کنند. همچنین:
\(\mathop {\lim }\limits_{x \to 1} \frac{{g(x) - g(1)}}{{x - 1}} = \left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} \frac{{x + 1 - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{x}{{x - 1}} = + \infty \\\mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} (x + 1) = 2\end{array} \right.\)
پس g’(1) وجود ندارد.
کار در کلاس صفحه 87 درس مشتق حسابان دوازدهم
پاسخ کار در کلاس صفحه 87 درس 4
جواب کار در کلاس صفحه 87 درس 4 حسابان دوازدهم
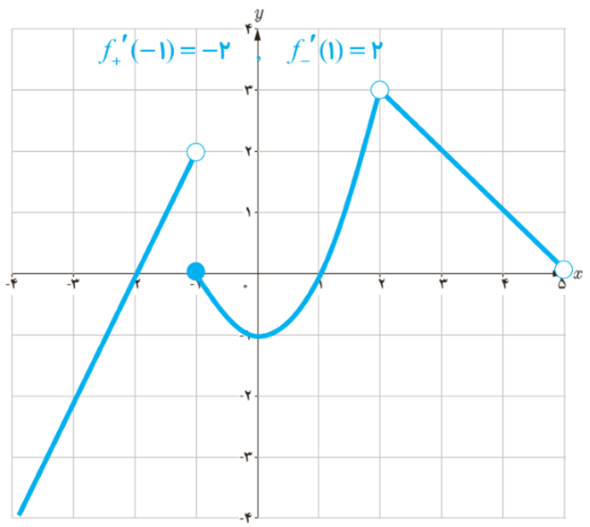
نشان دهید که مشتق تابع f در مثال قبل در x=-1 نیز موجود نیست.
در صورت امکان معادله نیم مماس های راست و چپ در x=-1 را بنویسید.
\(\begin{array}{*{20}{l}}\begin{array}{l}f'( - 1) = \mathop {\lim }\limits_{x \to - 1} \frac{{f(x) - f( - 1)}}{{x + 1}} = \\\\\mathop {\lim }\limits_{x \to - 1} \frac{{\left| {{x^2} - 1} \right| - 0}}{{x + 1}}\end{array}\\\begin{array}{l}\\{f_ + }^\prime ( - 1) = \mathop {\lim }\limits_{x \to - {1^ + }} \frac{{ - ({x^2} - 1)}}{{x + 1}} = \\\\\mathop {\lim }\limits_{x \to - {1^ + }} - (x - 1) = 2\\\\{f_ - }^\prime ( - 1) = \mathop {\lim }\limits_{x \to - {1^ - }} \frac{{({x^2} - 1)}}{{x + 1}} = \\\end{array}\\{\mathop {\lim }\limits_{x \to - {1^ - }} (x - 1) = - 2}\end{array}\)
ابتدا معادله نیم مماس راست را می نویسیم:
\(\begin{array}{l}m = {f_ + }^\prime ( - 1) = 2\\\\A\left| \begin{array}{l} - 1\\\\0\end{array} \right.\\\\y - {y_A} = m(x - {x_A})\\\\ \Rightarrow y - 0 = 2(x + 1)\\\\ \Rightarrow y = 2x + 2\end{array}\)
حال معادله نیم مماس چپ را می نویسیم:
\(\begin{array}{l}m = {f_ - }^\prime ( - 1) = - 2\\\\A\left| \begin{array}{l} - 1\\\\0\end{array} \right.\\\\y - {y_A} = m(x - {x_A})\\\\ \Rightarrow y - 0 = - 2(x + 1)\\\\ \Rightarrow y = - 2x - 2\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دوازدهم- آزمون آنلاین تمامی دروس پایه دوازدهم
- گام به گام تمامی دروس پایه دوازدهم
- ویدئو های آموزشی تمامی دروس پایه دوازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دوازدهم
- فلش کارت های آماده دروس پایه دوازدهم
- گنجینه ای جامع از انشاء های آماده پایه دوازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دوازدهم
کار در کلاس صفحه 89 درس مشتق حسابان دوازدهم
پاسخ کار در کلاس صفحه 89 درس 4
جواب کار در کلاس صفحه 89 درس 4 حسابان دوازدهم
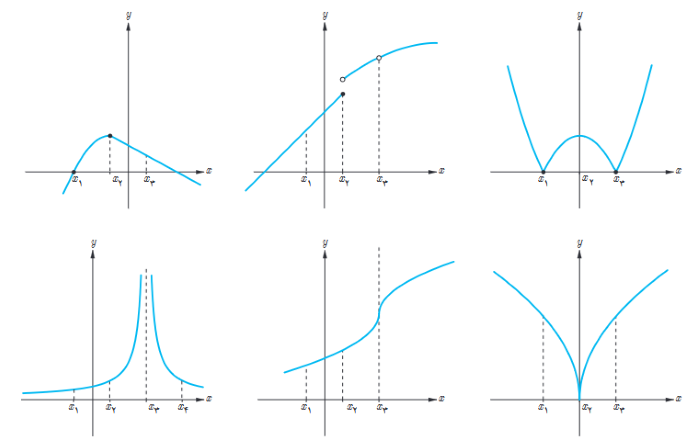
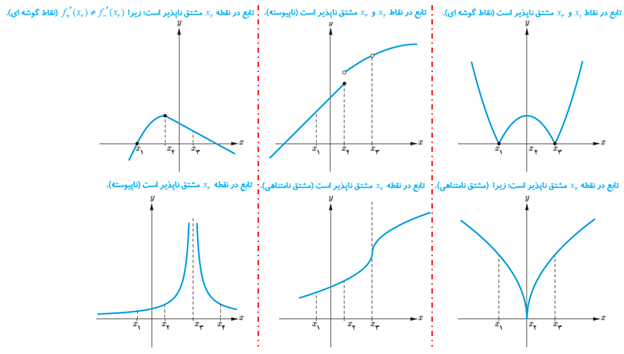
در شکل های زیر مشخص کنید که هر تابع در کدام نقطه یا نقاط مشخص شده مشتق پذیر نیست.
گام به گام کتاب های پایه دوازدهم
گام به گام جامع کتاب حسابان دوازدهم
گام به گام جامع کتاب فیزیک دوازدهم ریاضی
گام به گام جامع کتاب شیمی دوازدهم
گام به گام جامع کتاب هندسه دوازدهم
گام به گام جامع کتاب ریاضیات گسسته
گام به گام جامع کتاب فارسی دوازدهم
گام به گام جامع کتاب نگارش دوازدهم
گام به گام جامع کتاب عربی دوازدهم
گام به گام جامع کتاب زبان انگلیسی دوازدهم
گام به گام جامع کتاب کتاب کار انگلیسی دوازدهم
گام به گام جامع کتاب دین و زندگی دوازدهم
گام به گام جامع کتاب هویت اجتماعی
گام به گام جامع کتاب سلامت و بهداشت
گام به گام جامع کتاب مدیریت خانواده و سبک زندگی (پسران)
فعالیت صفحه 90 درس مشتق حسابان دوازدهم
پاسخ فعالیت صفحه 90 درس 4
جواب فعالیت صفحه 90 درس 4 حسابان دوازدهم
تابع f(x)=x2 را درنظر می گیریم.

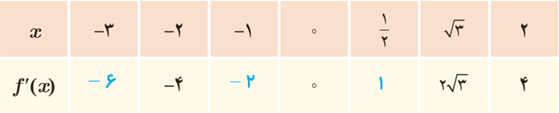
الف جدول زیر را کامل کنید (مشتق تابع در برخی نقاط حساب شده اند).

\(\begin{array}{l}f'\left( { - 2} \right) = \mathop {\lim }\limits_{x \to - 2} \frac{{f\left( x \right) - f\left( { - 2} \right)}}{{x - \left( { - 2} \right)}} = \mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} - 4}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \left( {x - 2} \right) = - 4\\\\f'\left( {\sqrt 3 } \right) = \mathop {\lim }\limits_{x \to - 2} \frac{{f\left( x \right) - f\left( {\sqrt 3 } \right)}}{{x - \sqrt 3 }} = \mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} - 3}}{{x - \sqrt 3 }} = \mathop {\lim }\limits_{x \to - 2} \frac{{\left( {x - 3} \right)\left( {x + 3} \right)}}{{x - \sqrt 3 }} = 2\sqrt 3 \\\\f'\left( 0 \right) = \mathop {\lim }\limits_{x \to - 0} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to - 2} \frac{{{x^2}}}{x} = 0\end{array}\)
ب می دانیم مشتق تابع در یک نقطه (در صورت وجود) برابر شیب خط مماس بر منحنی در آن نقطه است و از طرفی مماس بر منحنی در هر نقطه یکتاست، بنابراین f’(x) تابعی از x است.حدس می زنید در چه نقاطی مشتق تابع f(x)=x2 وجود دارد؟
الف
ب
با توجه به اینکه:
نمودار f(x)=x2 یک منحنی هموار و پیوسته است
فرمول مشتق آن، f′(x)=2x ، برای تمام اعداد حقیقی x تعریف شده و مقدار دارد.
حدس میزنیم که مشتق تابع f(x)=x2 در تمام نقاط x که عضو مجموعه اعداد حقیقی (R) هستند، وجود دارد.
کار در کلاس صفحه 92 درس مشتق حسابان دوازدهم
پاسخ کار در کلاس صفحه 92 درس 4
جواب کار در کلاس صفحه 92 درس 4 حسابان دوازدهم
اگر \(f\left( x \right) = \left\{ \begin{array}{l}5x\;\;\;\;x \ne 1\\2\;\;\;\;\;\;x = 1\end{array} \right.\) دامنه f و دامنه \(f’\) را محاسبه کنید و ضابطه \(f’\) را به دست آورید. نمودار \(f\) و نمودار \(f’\) را رسم کنید.
\({D_f} = \left\{ {x \in \mathbb{R}|x \ne 1} \right\} \cup \left\{ 1 \right\} = \mathbb{R}\)
تابع در نقطۀ \(x = 1\) پیوسته نیست؛ لذا \(f'(1)\) وجود ندارد، پس \({D_{f'}} = \mathbb{R} - \left\{ 1 \right\}\)
\(f'(x) = \left\{ \begin{array}{l}5\quad \quad x \ne 1\\\emptyset \quad \;\;\,x = 1\end{array} \right.\)
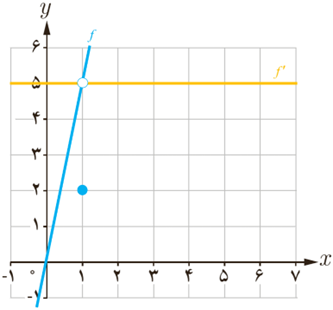
\((\emptyset )\) یعنی تعریف نشده!
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دوازدهم- آزمون آنلاین تمامی دروس پایه دوازدهم
- گام به گام تمامی دروس پایه دوازدهم
- ویدئو های آموزشی تمامی دروس پایه دوازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دوازدهم
- فلش کارت های آماده دروس پایه دوازدهم
- گنجینه ای جامع از انشاء های آماده پایه دوازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دوازدهم
کار در کلاس صفحه 95 درس مشتق حسابان دوازدهم
پاسخ کار در کلاس صفحه 95 درس 4
جواب کار در کلاس صفحه 95 درس 4 حسابان دوازدهم
1 مشتق تابع های زیر را به دست آورید:
\(f\left( x \right) = \frac{1}{{x - 4}}\) الف
\(g\left( x \right) = \sqrt x \left( {3{x^2} + 5} \right)\) ب
\(h\left( x \right) = \frac{x}{{2{x^2} + x - 1}}\) پ
الف
\(f\left( x \right) = \frac{1}{{x - 4}} \Rightarrow f'(x) = \frac{{ - 1}}{{{{(x - 4)}^2}}}\)
ب
\(g\left( x \right) = \sqrt x \left( {3{x^2} + 5} \right) \Rightarrow g'(x) = \frac{1}{{2\sqrt x }}(3{x^2} + 5) + \sqrt x (6x) = \frac{{15{x^2} + 5}}{{2\sqrt x }}\)
پ
\(h\left( x \right) = \frac{x}{{2{x^2} + x - 1}} \Rightarrow h'(x) = \frac{{1(2{x^2} + x - 1) - x(4x + 1)}}{{{{(2{x^2} + x - 1)}^2}}} = \frac{{ - 2{x^2} + x - 2}}{{{{(2{x^2} + x - 1)}^2}}}\)
2 اگر f و g توابع مشتق پذیر باشند و \(f(2)=3 \), \(f’(2)=5 \), \(g(2)=8\) و \(g’(2)=-6\) مقدار \((fg)’(2) \)و \((\frac{f}{g})'\left( 2 \right)\) را به دست آورید.
\(\begin{array}{l}(f.g)'(2) = f'(2).g(2) + f(2).g'(2) = 5 \times 8 + ( - 6) \times 3 = 22\\\\(\frac{f}{g})'(2) = \frac{{f'(2).g(2) - f(2).g'(2)}}{{{g^2}(2)}} = \frac{{5 \times 8 - ( - 6) \times 3}}{{{8^2}}} = \frac{{58}}{{64}} = \frac{{29}}{{32}}\end{array}\)
گام به گام کتاب های پایه دوازدهم
گام به گام جامع کتاب حسابان دوازدهم
گام به گام جامع کتاب فیزیک دوازدهم ریاضی
گام به گام جامع کتاب شیمی دوازدهم
گام به گام جامع کتاب هندسه دوازدهم
گام به گام جامع کتاب ریاضیات گسسته
گام به گام جامع کتاب فارسی دوازدهم
گام به گام جامع کتاب نگارش دوازدهم
گام به گام جامع کتاب عربی دوازدهم
گام به گام جامع کتاب زبان انگلیسی دوازدهم
گام به گام جامع کتاب کتاب کار انگلیسی دوازدهم
گام به گام جامع کتاب دین و زندگی دوازدهم
گام به گام جامع کتاب هویت اجتماعی
گام به گام جامع کتاب سلامت و بهداشت
گام به گام جامع کتاب مدیریت خانواده و سبک زندگی (پسران)
کار در کلاس صفحه 96 درس مشتق حسابان دوازدهم
پاسخ کار در کلاس صفحه 96 درس 4
جواب کار در کلاس صفحه 96 درس 4 حسابان دوازدهم
مشتق توابع زیر را به دست آورید.
\(f\left( x \right) = \sin x\;\tan x\) الف
\(g\left( x \right) = \frac{{5\cos x}}{{1 - \sin x}}\) ب
الف
\(f\left( x \right) = \sin x\;\tan x \Rightarrow f'(x) = \cos x\tan x + \sin x(1 + {\tan ^2}x)\)
ب
\(g\left( x \right) = \frac{{5\cos x}}{{1 - \sin x}} \Rightarrow g'(x) = \frac{{( - 5\sin x)(1 - \sin x) - (5\cos x)( - \cos x)}}{{{{(1 - \sin x)}^2}}} = \frac{{5 - 5\sin x}}{{{{(1 - \sin x)}^2}}} = \frac{5}{{1 - \sin x}}\)
کار در کلاس صفحه 97 درس مشتق حسابان دوازدهم
پاسخ کار در کلاس صفحه 97 درس 4
جواب کار در کلاس صفحه 97 درس 4 حسابان دوازدهم
مشتق تابع های زیر را به دست آورید.
\(f\left( x \right) = {\left( {{x^2} + 1} \right)^3}\left( {5x - 1} \right)\) الف
\(g\left( x \right) = {\cos ^3}x\) ب
\(h\left( x \right) = \sin \left( {3{x^2} + 5} \right)\) پ
الف
\(f\left( x \right) = {\left( {{x^2} + 1} \right)^3}\left( {5x - 1} \right) \Rightarrow f'(x) = 3(2x){({x^2} + 1)^2}(5x - 1) + {({x^2} + 1)^3}(5)\)
ب
\(g\left( x \right) = {\cos ^3}x \Rightarrow g'(x) = - 3\sin x{\cos ^2}x\)
پ
\(h\left( x \right) = \sin \left( {3{x^2} + 5} \right) \Rightarrow h'(x) = 6x\cos (3{x^2} + 5)\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دوازدهم- آزمون آنلاین تمامی دروس پایه دوازدهم
- گام به گام تمامی دروس پایه دوازدهم
- ویدئو های آموزشی تمامی دروس پایه دوازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دوازدهم
- فلش کارت های آماده دروس پایه دوازدهم
- گنجینه ای جامع از انشاء های آماده پایه دوازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دوازدهم
کار در کلاس صفحه 97 درس مشتق حسابان دوازدهم
پاسخ کار در کلاس صفحه 97 درس 4
جواب کار در کلاس صفحه 97 درس 4 حسابان دوازدهم
مشتق پذیری روی بازه های \([a,b)\) و \((a,b]\) را به طور مشابه تعریف کنید.
الف تابع f روی بازه \([a,b) \) مشتق پذیر است هرگاه …
ب تابع f روی بازه \((a,b]\) مشتق پذیر است هرگاه …
الف
f روی بازه های (a,b) مشتق پذیر باشد و در نقطۀ a مشتق راست داشته باشد.
ب
f روی بازه های (a,b) مشتق پذیر باشد و در نقطۀ b مشتق چپ داشته باشد.
گام به گام کتاب های پایه دوازدهم
گام به گام جامع کتاب حسابان دوازدهم
گام به گام جامع کتاب فیزیک دوازدهم ریاضی
گام به گام جامع کتاب شیمی دوازدهم
گام به گام جامع کتاب هندسه دوازدهم
گام به گام جامع کتاب ریاضیات گسسته
گام به گام جامع کتاب فارسی دوازدهم
گام به گام جامع کتاب نگارش دوازدهم
گام به گام جامع کتاب عربی دوازدهم
گام به گام جامع کتاب زبان انگلیسی دوازدهم
گام به گام جامع کتاب کتاب کار انگلیسی دوازدهم
گام به گام جامع کتاب دین و زندگی دوازدهم
گام به گام جامع کتاب هویت اجتماعی
گام به گام جامع کتاب سلامت و بهداشت
گام به گام جامع کتاب مدیریت خانواده و سبک زندگی (پسران)
کار در کلاس صفحه 98 درس مشتق حسابان دوازدهم
پاسخ کار در کلاس صفحه 98 درس 4
جواب کار در کلاس صفحه 98 درس 4 حسابان دوازدهم
اگر\(f\left( x \right) = \left\{ \begin{array}{l}2x + 4\;\;\;\;\;\;\;\;x < - 1\\{x^2} - 1\;\;\;\;\;\; - 1 \le x < 2\\ - x + 5\;\;\;\;\;\;\;2 < x < 5\end{array} \right.\) نمودار f را رسم کنید و مشتق پذیری f را روی بازه های \([-1,1] \)، \((2,5) \) و \([-2,0] \) بررسی کنید.
تابع در نقطۀ [1،1-] مشتق پذیر است.
تابع در نقطۀ (2،5) مشتق پذیر است.
تابع در نقطۀ [2،0-] مشتق پذیر نیست؛ زیرا در فاصلۀ [2،0-] پیوسته نیست، چون تابع در x=-1 ناپیوسته و مشتق ناپذیر است.
تمرین صفحه 99 درس مشتق حسابان دوازدهم
پاسخ تمرین صفحه 99 درس 4
جواب تمرین صفحه 99 درس 4 حسابان دوازدهم
1 دو تابع مختلف مانند f و g مثال بزنید که هر دو در x=2 پیوسته باشند ولی در این نقطه مشتق پذیر نباشند.
\(f(x) = \left| {x - 2} \right|\quad ,\quad g(x) = \left\{ \begin{array}{l}{x^2}\quad \quad ,x < 2\\x + 2\quad ,x \ge 2\end{array} \right.\)
2 با محاسبه مشتق راست و مشتق چپ توابع داده شده در نقطه A، نشان دهید که این توابع در نقطه A مشتق پذیر نیستند.

الف
\(\left\{ \begin{array}{l}{f_ + }^\prime (0) = 2(0) = 0\\{f_ - }^\prime (0) = - 1\end{array} \right.\)
وجود ندارد \({f^\prime }(0)\;:\)
ب
\(\left\{ \begin{array}{l}{f_ + }^\prime (1) = \frac{{ - 1}}{{{{(1)}^2}}} = - 1\\{f_ - }^\prime (1) = 0\end{array} \right.\)
وجود ندارد \({f^\prime }(1)\;:\)
پ
\(\left\{ \begin{array}{l}{f_ + }^\prime (4) = \frac{1}{2}\\{f_ - }^\prime (4) = \frac{1}{{2\sqrt 4 }} = \frac{1}{4}\end{array} \right.\)
وجود ندارد \({f^\prime }(2)\;:\)
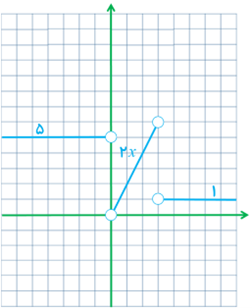
3 تابع \(f\left( x \right) = \left\{ \begin{array}{l}5x - 4\;\;\;\;\;\;\;\;x < 0\\{x^2}\;\;\;\;\;\;\;\;\;\;0 \le x \le 3\\x + 6\;\;\;\;\;\;\;\;\;\;x > 3\end{array} \right.\) داده شده است.
الف نمودار تابع f را رسم کنید.
ب با توجه به نمودار تابع f بگویید که چرا f’(0) و f’(3) وجود ندارند؟
پ ضابطه تابع مشتق را بنویسید.
ت نمودار تابع \(f’\) را رسم کنید.
الف

ب
\({f^\prime }(0)\) وجود ندارد چون تابع در \(x = 0\) ناپیوسته است.
\({f^\prime }(3)\) وجود ندارد \({f_ + }^\prime (3) = 1\quad ,{f_ - }^\prime (3) = 6\quad \to \)
پ
\(f'(x) = \left\{ \begin{array}{l}5\quad \quad x < 0\\2x\quad \;\,{\kern 1pt} 0 < x < 3\\1\quad \quad x > 3\end{array} \right.\)
ت
4 نمودار تابعی را رسم کنید که مشتق آن
الف در یک نقطه برابر صفر شود.
ب در x=2 برابر 3 شود
پ در تمام نقاط مثبت باشد.
ت در تمام نقاط یکسان باشد.
ث در تمام نقاط منفی باشد.
الف
ب
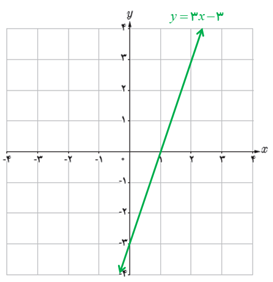
پ

ت
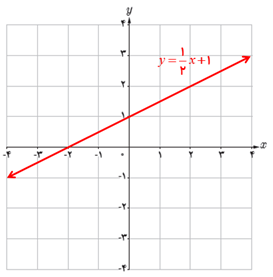
ث
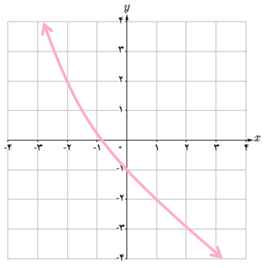
5
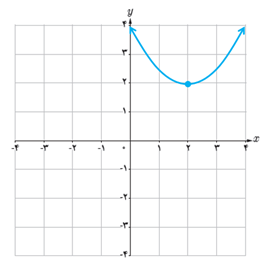
الف با استفاده از نمودار تابع \(f\left( x \right) = {x^2} + 2x + 3\) (شکل مقابل) مقادیر زیر را به ترتیب صعودی مرتب کنید.
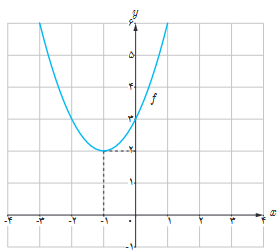
f'(3) و f’(0) و f’(-1) و f’(2)
ب صحت ادعای خود در (الف) را با محاسبه مشتق تابع\(f\left( x \right) = {x^2} + 2x + 3\) بررسی کنید.
پ تابع مشتق را رسم کنید.
الف
\(0 = f'( - 1) < f'(0) < f'(2) < f'(3)\)
ب
\(f'(x) = 2x + 2 \Rightarrow \left\{ \begin{array}{l}f'( - 1) = 0\\f'(0) = 2\\f'(2) = 6\\f'(3) = 8\end{array} \right.\)
پ
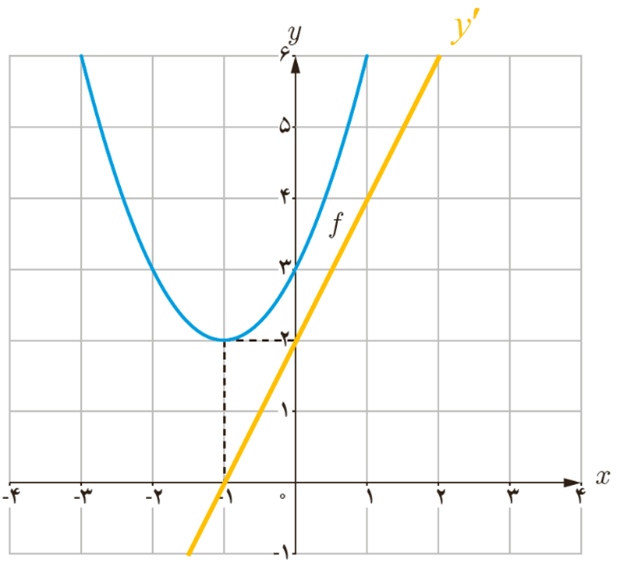
6 مشتق پذیری تابع\(f\left( x \right) = \left\{ \begin{array}{l}{x^2} + 3\;\;\;\;\;x \ge 1\\2x\;\;\;\;\;\;\;\;\;x < 1\end{array} \right.\) را در نقطه x=1 بررسی کنید.
تابع در نقطه \(x = 1\) ناپیوسته است؛ پس در این نقطه مشتق پذیر نیست \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f(x) = 1\\\mathop {\lim }\limits_{x \to {1^ - }} f(x) = 2\end{array} \right. \to \)
7 سه تابع مختلف مثال بزنید که مشتق آنها با هم برابر باشند.
\(\left\{ \begin{array}{l}f(x) = 3x\\g(x) = 3x - 10\\h(x) = 3x + 5\end{array} \right.\)
8 اگر \(f(x) = |x2-4|\) به کمک تعریف مشتق، مشتق پذیری f را در نقاط به طول های 2 و 2- بررسی کنید.
\(\left\{ \begin{array}{l}f(x) = \left\{ \begin{array}{l}{x^2} - 4\quad \quad \quad ,x < - 2\\ - ({x^2} - 4)\quad \;\,{\kern 1pt} {\kern 1pt} {\kern 1pt} , - 2 \le x \le 2\\{x^2} - 4\quad \quad \quad ,x > 2\end{array} \right.\\f'(x) = \left\{ \begin{array}{l}2x\quad \quad \quad ,x < - 2\\ - 2x\quad \;\,{\kern 1pt} \;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} , - 2 < x < 2\\2x\quad \quad \quad ,x > 2\end{array} \right.\end{array} \right.\quad \Rightarrow \quad \left\{ \begin{array}{l}\left\{ \begin{array}{l}{f_ + }^\prime (2) = 4\\{f_ - }^\prime (2) = - 4\end{array} \right. \Rightarrow {f_ + }^\prime (2) \ne {f_ - }^\prime (2) \Rightarrow \cancel{\exists }f'(2)\\\left\{ \begin{array}{l}{f_ + }^\prime ( - 2) = 4\\{f_ - }^\prime ( - 2) = - 4\end{array} \right. \Rightarrow {f_ + }^\prime ( - 2) \ne {f_ - }^\prime ( - 2) \Rightarrow \cancel{\exists }f'( - 2)\end{array} \right.\)
9 مشتق تابع \(f\left( x \right) = \sqrt[3]{{{x^2}}}\) را به دست آورده و مشخص کنید در چه نقطه ای مماس قائم دارد؟
\(\begin{array}{l}f(x) = \sqrt[3]{{{x^2}}} = {x^{\frac{2}{3}}} \Rightarrow f'(x) = \frac{2}{3}{x^{\frac{2}{3} - 1}} = \frac{2}{3}{x^{\frac{{ - 1}}{3}}} = \frac{2}{{3\sqrt[3]{x}}}\\ \Rightarrow \left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to \;{0^ - }} f'(x) = \mathop {\lim }\limits_{x \to \;{0^ - }} \frac{2}{{3\sqrt[3]{x}}} = \frac{2}{{{0^ - }}} = - \infty \\\mathop {\lim }\limits_{x \to \;{0^ + }} f'(x) = \mathop {\lim }\limits_{x \to \;{0^ + }} \frac{2}{{3\sqrt[3]{x}}} = \frac{2}{{{0^ + }}} = + \infty \end{array} \right. \Rightarrow x = 0\end{array}\)
تابع در نقطه\(x = 0\) پیوسته است و ومماس قائم دارد.
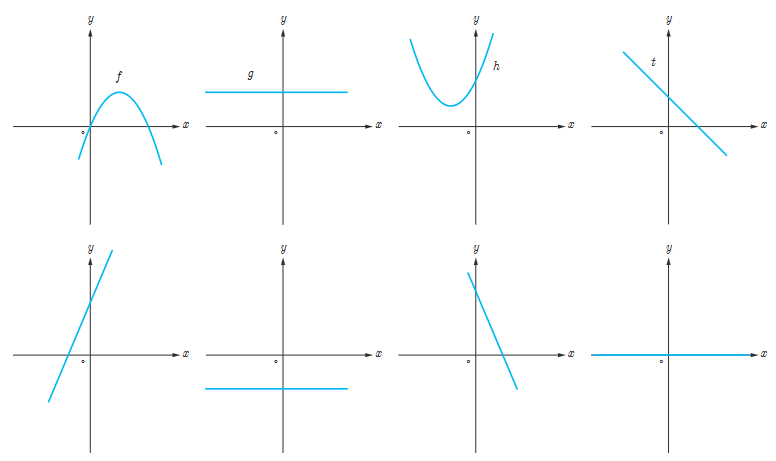
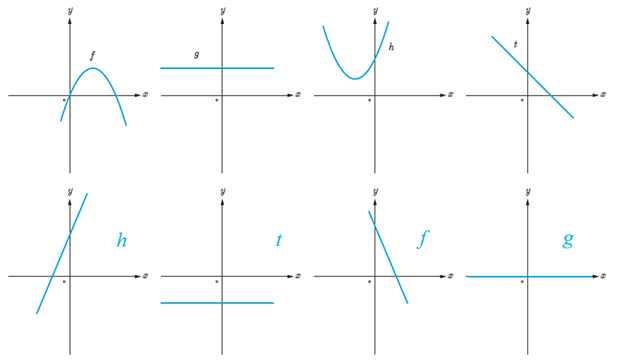
10 نمودار توابع f و g و h و t را به نمودار مشتق آنها، نظیر کنید.
11 نمودار توابع f و g را در شکل مقابل درنظر بگیرید.
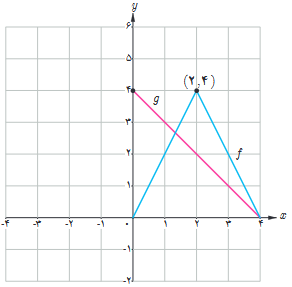
الف اگر h(x)=f(x).g(x) مطلوب است h’(2) ، h’(1) و h’(3)
ب اگر \(k\left( x \right) = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) مطلوب است k’(2) ، k’(1) و k’(3)
الف
\(\begin{array}{l}\left\{ \begin{array}{l}f(1) = 2\\f'(1) = 2\\g(1) = 3\\g'(1) = - 1\end{array} \right. \Rightarrow h'(1) = f'(1) \cdot g(1) + f(1) \cdot g'(1) = 2 \times 3 + 2 \times ( - 1) = 4\\\left\{ \begin{array}{l}f(2) = 4\\f'(2) = \xcancel{{}}\\g(2) = 2\\g'(2) = - 1\end{array} \right. \Rightarrow h'(2) = f'(2) \cdot g(2) + f(2) \cdot g'(2) = \xcancel{{}} \Rightarrow \xcancel{\exists }h'(2)\\\left\{ \begin{array}{l}f(3) = 2\\f'(3) = - 2\\g(3) = 1\\g'(3) = - 1\end{array} \right. \Rightarrow h'(3) = f'(3) \cdot g(3) + f(3) \cdot g'(3) = ( - 2) \times 1 + 2 \times ( - 1) = - 4\end{array}\)
ب
\(\begin{array}{l}\left\{ \begin{array}{l}f(1) = 2\\f'(1) = 2\\g(1) = 3\\g'(1) = - 1\end{array} \right. \Rightarrow k'(1) = \frac{{f'(1) \cdot g(1) - f(1) \cdot g'(1)}}{{{g^2}(1)}} = \frac{{2 \times 3 - 2 \times ( - 1)}}{{{3^2}}} = \frac{8}{9}\\\left\{ \begin{array}{l}f(2) = 4\\f'(2) = \xcancel{{}}\\g(2) = 2\\g'(2) = - 1\end{array} \right. \Rightarrow k'(2) = \frac{{f'(2) \cdot g(2) - f(2) \cdot g'(2)}}{{{g^2}(2)}} = \xcancel{{}} \Rightarrow \xcancel{\exists }k'(2)\\\left\{ \begin{array}{l}f(3) = 2\\f'(3) = - 2\\g(3) = 1\\g'(3) = - 1\end{array} \right. \Rightarrow k'(3) = \frac{{f'(3) \cdot g(3) - f(3) \cdot g'(3)}}{{{g^2}(3)}} = \frac{{( - 2) \times 1 - 2 \times ( - 1)}}{{{1^2}}} = 0\end{array}\)
12 اگر f’(1)=3 و g’(1)=5 مطلوب است، \((f+g)’(1)\) و \((3f+2g)’(1)\)
\(\begin{array}{l}(f + g)'(1) = f'(1) + g'(1) = 3 + 5 = 8\\\\(3f + 2g)'(1) = 3f'(1) + 2g'(1) = 3 \times 3 + 2 \times 5 = 19\end{array}\)
13 اگر \(f\left( x \right) = \left\{ \begin{array}{l}{x^2}\;\;\;\;x \le 0\\x\;\;\;\;\;x > 0\end{array} \right.\) نشان دهید \(f{'_ + }(0)\) و \(f{'_ - }(0)\) موجودند ولی f’(0) موجود نیست.
\(f(x) = \left\{ \begin{array}{l}{x^2}\quad \quad x \le 0\\x\quad \quad \,\;x > 0\end{array} \right. \Rightarrow f'(x) = \left\{ \begin{array}{l}2x\quad \quad x < 0\\1\quad \quad \,\;\;x > 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{f_ - }^\prime (0) = 2 \times 0 = 0\\{f_ + }^\prime (0) = 1\end{array} \right. \Rightarrow {f_ - }^\prime (0) \ne {f_ + }^\prime (0) \Rightarrow \cancel{\exists }{f^\prime }(0)\)
14 مشتق توابع داده شده را به دست آورید.
\(f\left( x \right) = \left( {3{x^2} - 4} \right){\left( {2x - 5} \right)^2}\) الف
\(f\left( x \right) = \left( {\sqrt {3x + 2} } \right)\left( {{x^3} + 1} \right)\) ب
\(f\left( x \right) = \frac{{{x^2} - 3x + 1}}{{ - 3x + 2}}\) پ
\(f\left( x \right) = \frac{{9x - 2}}{{\sqrt x }}\) ت
الف
\(f\left( x \right) = \left( {3{x^2} - 4} \right){\left( {2x - 5} \right)^2} \Rightarrow f'(x) = 6x{(2x - 5)^3} + 3(2){(2x - 5)^2}(3{x^2} - 4)\)
ب
\(f\left( x \right) = \left( {\sqrt {3x + 2} } \right)\left( {{x^3} + 1} \right) \Rightarrow f'(x) = \frac{{(2x - 3)( - 3x + 2) - ({x^2} - 3x + 1)( - 3)}}{{{{( - 3x + 2)}^2}}}\)
پ
\(f\left( x \right) = \frac{{{x^2} - 3x + 1}}{{ - 3x + 2}} \Rightarrow f'(x) = \frac{3}{{2\sqrt {3x + 2} }}({x^3} + 1) + 3{x^2}\sqrt {3x + 2} \)
ت
\(f\left( x \right) = \frac{{9x - 2}}{{\sqrt x }} \Rightarrow f'(x) = \frac{{9\sqrt x - \left( {9x - 2} \right)\frac{1}{{2\sqrt x }}}}{x}\)
15 مشتق توابع مثلثاتی زیر را به دست آورید.
\(f\left( x \right) = {\sin ^3}x + {\cos ^2}x\) الف
\(f\left( x \right) = {\tan ^2}x - 2\cos x\) ب
\(f\left( x \right) = \frac{{1 - \sin x}}{{1 + \sin x}}\) پ
\(f\left( x \right) = \sin x\;\cos 2x\) ت
الف
\(f\left( x \right) = {\sin ^3}x + {\cos ^2}x \Rightarrow f'(x) = 3\cos x{\sin ^2}x - 2\sin x\cos x\)
ب
\(f\left( x \right) = {\tan ^2}x - 2\cos x \Rightarrow f'(x) = \frac{{ - \cos x(1 + \sin x) - (1 - \sin x)cosx}}{{{{(1 + \sin x)}^2}}} = \frac{{ - 2\cos x}}{{{{(1 + \sin x)}^2}}}\)
پ
\(f\left( x \right) = \frac{{1 - \sin x}}{{1 + \sin x}} \Rightarrow f'(x) = 2(1 + {\tan ^2}x)\tan x + 2\sin x\)
ت
\(f\left( x \right) = \sin x\;\cos 2x \Rightarrow f'(x) = \cos x\cos 2x - 2\sin x\sin 2x\)
16 اگر \(f\left( x \right) = {\sin ^2}x - \cos 2x\) مقادیر زیر را حساب کنید.
\(f''\left( {\frac{\pi }{6}} \right)\) الف
\(f''\left( {\frac{\pi }{2}} \right) - f'\left( {\frac{\pi }{2}} \right)\) ب
\(\begin{array}{l}f'(x) = 2\cos x\sin x + 2\sin 2x = \sin 2x + 2\sin 2x = 3\sin 2x\\\\f''(x) = 6\cos 2x\end{array}\)
الف
\(f''\left( {\frac{\pi }{6}} \right) = 6\cos (2 \times \frac{\pi }{6}) = 6\cos (\frac{\pi }{3}) = 6 \times \frac{1}{2} = 3\)
ب
\(f''\left( {\frac{\pi }{2}} \right) - f'\left( {\frac{\pi }{2}} \right) = 6\cos (2 \times \frac{\pi }{2}) - 3sin(2 \times \frac{\pi }{2}) = 6\cos (\pi ) - 3sin(\pi ) = - 6\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دوازدهم- آزمون آنلاین تمامی دروس پایه دوازدهم
- گام به گام تمامی دروس پایه دوازدهم
- ویدئو های آموزشی تمامی دروس پایه دوازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دوازدهم
- فلش کارت های آماده دروس پایه دوازدهم
- گنجینه ای جامع از انشاء های آماده پایه دوازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دوازدهم
کار در کلاس صفحه 104 درس مشتق حسابان دوازدهم
پاسخ کار در کلاس صفحه 104 درس 4
جواب کار در کلاس صفحه 104 درس 4 حسابان دوازدهم
نمودار زیر موقعیت یک ذره را در لحظه t نمایش می دهد. مقادیر زیر را از کوچک به بزرگ مرتب کنید: (محاسبۀ عددی لازم نیست.)
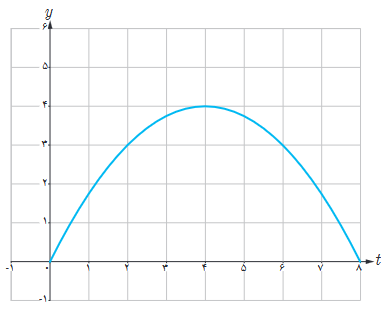
A سرعت متوسط بین t=1 و t=3
B سرعت متوسط بین t=5 و t=6
C سرعت لحظه ای در t=1
D سرعت لحظه ای در t=3
E سرعت لحظه ای در t=5
F سرعت لحظه ای در t=6
گام به گام کتاب های پایه دوازدهم
گام به گام جامع کتاب حسابان دوازدهم
گام به گام جامع کتاب فیزیک دوازدهم ریاضی
گام به گام جامع کتاب شیمی دوازدهم
گام به گام جامع کتاب هندسه دوازدهم
گام به گام جامع کتاب ریاضیات گسسته
گام به گام جامع کتاب فارسی دوازدهم
گام به گام جامع کتاب نگارش دوازدهم
گام به گام جامع کتاب عربی دوازدهم
گام به گام جامع کتاب زبان انگلیسی دوازدهم
گام به گام جامع کتاب کتاب کار انگلیسی دوازدهم
گام به گام جامع کتاب دین و زندگی دوازدهم
گام به گام جامع کتاب هویت اجتماعی
گام به گام جامع کتاب سلامت و بهداشت
گام به گام جامع کتاب مدیریت خانواده و سبک زندگی (پسران)
کار در کلاس صفحه 105 درس مشتق حسابان دوازدهم
پاسخ کار در کلاس صفحه 105 درس 4
جواب کار در کلاس صفحه 105 درس 4 حسابان دوازدهم
الف آهنگ متوسط رشد در بازه زمانی [0,25] چقدر است؟
ب آهنگ لحظه ای تغییر قد کودک را در 25 ماهگی و 49 ماهگی، با هم مقایسه کنید. کدام یک بیشتر است؟
پ اگر قد علی در 16 ماهگی، 80 سانتی متر و در 36 ماهگی، 95 سانتی متر باشد، آهنگ متوسط تغییر رشد او را در این فاصله حساب کنید و با نمودار بالا مقایسه کنید.
الف
سانتی متر / ماه \(\frac{{f(25) - f(0)}}{{25 - 0}} = \frac{{7\sqrt {25} + 50 - 50}}{{25}} = \frac{7}{5} = 1/4\)
ب
سانتی متر / ماه \(f'(x) = \frac{7}{{2\sqrt x }} \Rightarrow f'(25) = \frac{7}{{2\sqrt {25} }} = \frac{7}{{10}} = 0/7\)
سانتی متر / ماه \(f'(49) = \frac{7}{{2\sqrt {49} }} = \frac{7}{{14}} = 0/5\)
\(f'(49) < f'(25)\)
پ
سانتی متر / ماه \( = \frac{{f(36) - f(16)}}{{36 - 16}} = \frac{{95 - 80}}{{20}} = \frac{3}{4} = 0/75\) =آهنگ متوسط
کار در کلاس صفحه 108 درس مشتق حسابان دوازدهم
پاسخ کار در کلاس صفحه 108 درس 4
جواب کار در کلاس صفحه 108 درس 4 حسابان دوازدهم
با توجه به مثال قبل:
الف سرعت جسم هنگام پرتاب و هنگام برخورد به زمین را به دست آورید.
ب سرعت متوسط جسم را در بازه زمانی [5,8] به دست آورید.
پ لحظاتی را معلوم کنید که سرعت جسم \(35 m/s \)و \(-35 m/s\) است.
الف
\(t = 0 \Rightarrow h'(0) = 40m/ s\) :هنگام پرتاب
\(t = 8 \Rightarrow h'(0) = 40 m/s\) :هنگام برخورد به زمین
ب
\( = \frac{{h(8) - h(5)}}{{8 - 5}} = \frac{{0 - 75}}{3} = - 25\;m/s\) سرعت متوسط
پ
\( = h'(t) = - 10t + 40 \Rightarrow \left\{ \begin{array}{l}h'(t) = 35 \Rightarrow 35 = - 10t + 40 \Rightarrow t = 0/5\;s\\h'(t) = - 35 \Rightarrow - 35 = - 10t + 40 \Rightarrow t = 7/5\;s\end{array} \right.\) سرعت لحظه ای
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه دوازدهم- آزمون آنلاین تمامی دروس پایه دوازدهم
- گام به گام تمامی دروس پایه دوازدهم
- ویدئو های آموزشی تمامی دروس پایه دوازدهم
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس پایه دوازدهم
- فلش کارت های آماده دروس پایه دوازدهم
- گنجینه ای جامع از انشاء های آماده پایه دوازدهم
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه پایه دوازدهم
تمرین صفحه 108 درس مشتق حسابان دوازدهم
پاسخ تمرین صفحه 108 درس 4
جواب تمرین صفحه 108 درس 4 حسابان دوازدهم
1 جدول زیر درجه حرارت T (سانتی گراد) را در شهری از ساعت 8 تا 18 در یک روز نشان می دهد.

آهنگ تغییر متوسط درجه حرارت نسبت به زمان را:
الف از ساعت 8 تا ساعت 12 به دست آورید.
ب از ساعت 12 تا ساعت 18 به دست آورید.
پ پاسخ ها را تفسیر کنید.
الف
\(\frac{{T(12) - T(8)}}{{12 - 8}} = \frac{{19 - 11}}{4} = 2\)
ب
\(\frac{{T(18) - T(12)}}{{18 - 12}} = \frac{{9 - 19}}{6} = - \frac{5}{3}\)
پ
در بازه ی زمانی ساعت 8 تا ساعت 12 ظهر، درجه حرارت با آهنگ 2 درجه سانتی گراد در ساعت در حال افزایش است. اما در بازه ی زمانی ساعت 12 ظهر تا ساعت 18 درجه حرارت با آهنگ \( - \;\frac{5}{3}\) درجه سانتی گراد در ساعت در حال کاهش است.
2 کسری از جمعیت یک شهر که به وسیله یک ویروس آلوده شده اند برحسب زمان (هفته) در نمودار روبه رو نشان داده شده است.
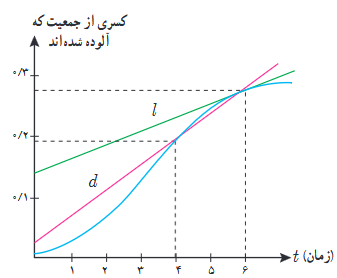
الف شیب خطوط l و d چه چیز هایی را نشان می دهند.
ب گسترش آلودگی در کدام یک از زمان های t=2 ، t=1 یا t=3 بیشتر است؟
پ قسمت ب را برای t=5 ، t=4 و t=6 بررسی کنید.
الف
شیب خطl ، آهنگ تغییر لحظه ای کسری از جمعیت آلوده شده در لحظۀ t=6 (هفتۀ ششم) نشان می دهد.
شیب خطd ، آهنگ تغییر متوسط کسری از جمعیت آلوده شده در فاصلۀ زمانیt=4 تا t=6 (هفتۀ چهارم تا هفتۀ ششم) نشان می دهد.
ب
در t=3 (هفتۀ سوم).
پ
در t=4 (هفتۀ چهارم).
3 نمودار روبه رو نمایش میزان فروش تعداد نوعی کالا (N) پس از صرف t میلیون تومان هزینه برای تبلیغ است.
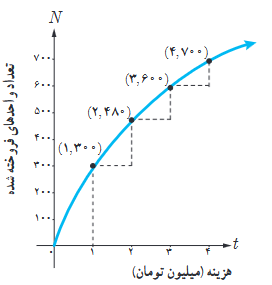
الف آهنگ تغییر N برحسب t را وقتی t از 0 تا 1، 1 تا 2 ، 2 تا 3 و 3 تا 4 تغییر می کند به دست آورید.
ب به نظر شما چرا آهنگ تغییرات، وقتی که مقادیر t افزایش می یابند، در حال کاهش است؟
الف
ب
زیرا با افزایش هزینه، تعداد کالاهای فروخته شده کم می شود، و رشد کمتری دارد. در نتیجه خریداران کم می شوند.
4 معادله حرکت متحرکی به صورت \(f\left( t \right) = {t^2} - t + 10\) برحسب متر در بازه زمانی [0,5] (t بر حسب ثانیه) داده شده است. در کدام لحظه سرعت لحظه ای با سرعت متوسط در بازهٔ زمانی [0,5] با هم برابرند؟
\( = \frac{{f(5) - f(0)}}{{5 - 0}} = \frac{{30 - 10}}{5} = 4m/s\) سرعت متوسط
\( = 2t - 1 \Rightarrow 2t - 1 = 4 \Rightarrow t = 2/5\;s\) سرعت لحظه ای
5 توپی از یک پل به ارتفاع 11 متر به هوا پرتاب می شود. F(t) نشان دهنده فاصله توپ از سطح زمین در زمان t است. برخی از مقادیر f(t) در جدول زیر نمایش داده شده است.

بر اساس جدول کدام یک از مقادیر زیر می تواند سرعت توپ را هنگامی که در ارتفاع نظیر زمان 0/4 ثانیه است، نشان دهد؟
\(1/23 m/s\) الف
\(12/91 m/s\) ب
\(11/5 m/s\) پ
\(16/03 m/s\) ت
\(\left\{ \begin{array}{l}\frac{{f(0/4) - f(0/3)}}{{0/1}} = 12\;m/s\\\frac{{f(0/5) - f(0/4)}}{{0/1}} = 11\;m/s\end{array} \right. \Rightarrow f'(0/4) = \frac{{12 + 11}}{2} = 11/5\;m/s\)
لذا گزینه (ج) جواب صحیح است.
6 کدام یک از عبارات زیر درست و کدام یک نادرست است:
الف آهنگ تغییر متوسط تابعی مانند f در بازه [0,1] همیشه کمتر از شیب آن منحنی در نقطه است.
ب اگر تابعی صعودی باشد، آهنگ تغییر متوسط آن، همواره صعودی است.
پ تابعی وجود ندارد که برای آن هم f’(a)=0 و هم f(a)=0
الف
نادرست
ب
نادرست

پ
نادرست؛ مثلاً
\(\left\{ \begin{array}{l}y = f(x) = {(x - 1)^2}\\a = 1\end{array} \right. \Rightarrow f'(x) = 2(x - 1) \Rightarrow f(a) = f'(a) = 0\)
7 یک توده باکتری پس از t ساعت دارای جرم \(m\left( t \right) = \sqrt t + 2{t^3}\) گرم است.
الف جرم این توده باکتری در بازه زمانی \(3 \le t \le 4\) چند گرم افزایش می یابد؟
ب آهنگ رشد جرم توده باکتری در لحظه t=3 چقدر است؟
الف
\(\frac{{m(4) - m(3)}}{{4 - 3}} = \frac{{130 - \sqrt 3 - 54}}{1} \simeq 74\;g\)
ب
\(m'(t) = \frac{1}{{2\sqrt t }} + 6{t^2} \Rightarrow m'(3) = \frac{1}{{2\sqrt 3 }} + 6{(3)^2} \simeq 54/3\;g\)
8 گنجایش ظرفی 40 لیتر مایع است. در لحظهٔ t=0 سوراخی در ظرف ایجاد می شود. اگر حجم مایع باقی مانده در ظرف پس از t ثانیه از رابطه \(V = 40{\left( {1 - \frac{t}{{100}}} \right)^2}\) به دست آید:
الف آهنگ تغییر متوسط حجم مایع در بازه زمانی [0,1] چقدر است؟
ب در چه زمانی، آهنگ تغییر لحظه ای حجم برابر آهنگ تغییر متوسط آن در بازه [0,100] می شود؟
الف
لیتر \(\frac{{V(1) - V(0)}}{{1 - 0}} = 39/204 - 40 = - 0/796\)
ب
\(\left. \begin{array}{l}\frac{{V(100) - V(0)}}{{100 - 0}} = - 0/4\\V'(t) = - 0/8(1 - \frac{t}{{100}})\end{array} \right\} \Rightarrow - 0/8(1 - \frac{t}{{100}}) = - 0/4 \to 1 - \frac{t}{{100}} = \frac{1}{2} \Rightarrow t = 50\;s\)



1736019749.png)