جواب تمرین صفحه 22 درس 1 ریاضی دوازدهم تجربی (تابع)
تعداد بازدید : 86.5Mپاسخ تمرین صفحه 22 ریاضی دوازدهم تجربی
-گام به گام تمرین صفحه 22 درس تابع
-تمرین صفحه 22 درس 1
-شما در حال مشاهده جواب تمرین صفحه 22 ریاضی دوازدهم تجربی هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 اگر\(f = \left\{ {\left( {7,8} \right),\left( {5,3} \right),\left( {9,8} \right),\left( {11,4} \right)} \right\}\) و\(g = \left\{ {\left( {5,7} \right),\left( {3,5} \right),\left( {7,9} \right),\left( {9,11} \right)} \right\}\) ، توابع fog و gof را به دست آورید.
\(\begin{array}{l}fog = \left\{ {(5\;,\;8)\;,\;(3\;,\;3)\;,\;(7\;,\;8)\;,\;(9\;,\;4)} \right\}\\gof = \left\{ {(5\;,\;5)} \right\}\end{array}\)
2 در هر قسمت موارد خواسته شده را در صورت امکان به دست آورید.
\(f\left( x \right) = {x^2} - 5\;\;;\;\;g\left( x \right) = \sqrt {x + 6} \;\;:\;\;{D_{fog}}\;,\;\left( {fog} \right)\left( x \right)\) الف
\(f\left( x \right) = \sqrt {3 - 2x} \;\;;\;\;g\left( x \right) = \frac{6}{{3x - 5}}\;\;:\;\;{D_{fog}}\;,\;\left( {fog} \right)\left( x \right)\) ب
\(f\left( x \right) = \sqrt {x + 2} \;\;;\;\;g\left( x \right) = \sqrt {{x^2} - 16} \;\;:\;\;{D_{gof}}\;,\;\left( {gof} \right)\left( x \right)\) پ
\(f\left( x \right) = \sin x\;\;;\;\;g\left( x \right) = \sqrt x \;\;:\;\;{D_{gof}}\;,\;\left( {gof} \right)\left( x \right)\) ت
الف
\(\begin{array}{l}\left\{ \begin{array}{l}f(x) = {x^2} - 5\quad \; \to \quad {D_f} = \mathbb{R}\\g(x) = \sqrt {x + 6} \quad \to \quad {D_g} = \left[ { - 6\;,\; + \infty } \right)\end{array} \right.\\\\ \Rightarrow {D_{fog}} = \left\{ {x \in {D_g}|g(x) \in {D_f}} \right\}\\\\ = \left\{ {\left[ { - 6\;,\; + \infty } \right)|\sqrt {x + 6} \in \mathbb{R}} \right\} = \left\{ {\left[ { - 6\;,\; + \infty } \right)|\sqrt {x + 6} \ge 0} \right\}\\\\ \Rightarrow {D_{fog}} = \left[ { - 6\;,\; + \infty } \right) \cap \left[ { - 6\;,\; + \infty } \right) = \left[ { - 6\;,\; + \infty } \right)\\\\fog(x) = f(g(x)) = {(g(x))^2} - 5 = {(\sqrt {x + 6} )^2} - 5 = x + 1\end{array}\)
ب
\(\begin{array}{l}\left\{ \begin{array}{l}f(x) = \sqrt {3 - 2x} \quad \; \to \quad {D_f} = \left( { - \;\infty \;,\;\frac{3}{2}} \right]\\g(x) = \frac{6}{{3x - 5}}\quad \;\;\;\, \to \quad {D_g} = \mathbb{R} - \left\{ {\frac{5}{3}} \right\}\end{array} \right.\\\\ \Rightarrow {D_{fog}} = \left\{ {x \in {D_g}|g(x) \in {D_f}} \right\}\\\\ = \left\{ {\mathbb{R} - \left\{ {\frac{5}{3}} \right\}|\frac{6}{{3x - 5}} \le \frac{3}{2}} \right\}\\\\\frac{6}{{3x - 5}} - \frac{3}{2} \le 0 \Rightarrow \frac{{ - 9x + 27}}{{6x - 10}} \le 0\\\\ \Rightarrow x \in \mathbb{R} - \left[ {\frac{5}{3}\;,\;3} \right)\\\\ \Rightarrow {D_{fog}} = \left\{ {\mathbb{R} - \left\{ {\frac{5}{3}} \right\}|\mathbb{R} - \left[ {\frac{5}{3}\;,\;3} \right)} \right\}\\\\ = \mathbb{R} - \left\{ {\frac{5}{3}} \right\} \cap \mathbb{R} - \left[ {\frac{5}{3}\;,\;3} \right) = \mathbb{R} - \left[ {\frac{5}{3}\;,\;3} \right)\\\\fog(x) = f(g(x)) = \sqrt {3 - 2g(x)} \\\\ = \sqrt {3 - 2\left( {\frac{6}{{3x - 5}}} \right)} = \sqrt {\frac{{9x - 27}}{{3x - 5}}} \end{array}\)
تعیین علامت عبارت \(\frac{{ - 9x + 27}}{{6x - 10}} \le 0\) :

پ
\(\begin{array}{l}\left\{ \begin{array}{l}f(x) = \sqrt {x + 2} \quad \;\,\;\, \to \quad {D_f} = \left[ { - 2\;,\; + \infty } \right)\\g(x) = \sqrt {{x^2} - 16} \quad \to \quad {D_g} = \mathbb{R} - \left( { - 4\;,\;4} \right)\end{array} \right.\\\\ \Rightarrow {D_{gof}} = \left\{ {x \in {D_f}|f(x) \in {D_g}} \right\}\\\\ = \left\{ {\left[ { - 2\;,\; + \infty } \right)|\sqrt {x + 2} \in \mathbb{R} - \left( { - 4\;,\;4} \right)} \right\}\\\\ = \left\{ {\left[ { - 2\;,\; + \infty } \right)|\sqrt {x + 2} \ge 4} \right\}\\\\ = \left\{ {\left[ { - 2\;,\; + \infty } \right)|x \ge 14} \right\} = \left\{ {\left[ { - 2\;,\; + \infty } \right)|} \right\} = \left[ { - 2\;,\; + \infty } \right) \cap \left[ {14\;,\; + \infty } \right)\\\\ \Rightarrow {D_{gof}} = \left[ {14\;,\; + \infty } \right)\\\\gof(x) = g(f(x)) = \sqrt {{{\left( {\sqrt {x + 2} } \right)}^2} - 16} = \sqrt {x - 14} \end{array}\)
ت
\(\begin{array}{l}\left\{ \begin{array}{l}f(x) = \sin x\quad \; \to \quad {D_f} = \mathbb{R}\\g(x) = \sqrt x \quad \;\;\,\, \to \quad {D_g} = \left[ {0\;,\; + \infty } \right)\end{array} \right.\\\\ \Rightarrow {D_{gof}} = \left\{ {x \in {D_f}|f(x) \in {D_g}} \right\}\\\\ = \left\{ {\mathbb{R}|\sin x \in \left[ {0\;,\; + \infty } \right)} \right\}\\\\ = \left\{ {\mathbb{R}|\sin x \ge 0} \right\} = \left\{ {\mathbb{R}|\left[ {2k\pi \;,\;2k\pi + \pi } \right]\quad ,\quad k \in \mathbb{Z}} \right\}\\\\ = \mathbb{R} \cap \left[ {2k\pi \;,\;2k\pi + \pi } \right]\quad ,\quad k \in \mathbb{Z}\\\\ \Rightarrow {D_{gof}} = \left[ {2k\pi \;,\;2k\pi + \pi } \right]\quad ,\quad k \in \mathbb{Z}\\\\gof(x) = g(f(x)) = \sqrt {\sin x} \end{array}\)
3 اگر \(f\left( {g\left( x \right)} \right) = 3{x^2} - 6x + 14\) و\(f\left( x \right) = 3x - 4\) ، ضابطۀ تابع g(x) را به دست آورید.
\(\begin{array}{l}\left\{ \begin{array}{l}f(g(x)) = 3{x^2} - 6x + 14\\f(x) = 3x - 4\\g(x) = ?\end{array} \right.\\\\ \Rightarrow \left\{ \begin{array}{l}f(g(x)) = 3g(x) - 4 = 3{x^2} - 6x + 14\\ \Rightarrow 3g(x) = 3{x^2} - 6x + 18\end{array} \right.\\\\ \Rightarrow g(x) = {x^2} - 2x + 6\end{array}\)
4 مشخص کنید کدام یک از جملات زیر درست و کدام یک نادرست است؟
الف اگر \(f\left( x \right) = {x^2} - 4\) و\(g\left( x \right) = \sqrt {{x^2} - 4} \) ؛ آنگاه \((fog)(5)=-25\).
ب برای دو تابع f و g که f≠g تساوی \((fog)(x)=(gof)(x)\) هیچ وقت برقرار نیست.
پ اگر f(7)=5 و g(4)=7، آنگاه \((fog)(4)=5\).
ت اگر \(f\left( x \right) = \sqrt x \) و \(g(x)=2x-1\)، آنگاه \((fog)(5)=g(2)\).
الف
نادرست
\(\begin{array}{l}fog(5) = f(g(5)) = {(g(5))^2} - 4\\ = {(\sqrt {{5^2} - 4} )^2} - 4 = 21 - 4 = 17\end{array}\)
ب
نادرست
\(\begin{array}{l}\left\{ \begin{array}{l}f(x) = 3x\\g(x) = 2x\end{array} \right. \to \left\{ \begin{array}{l}fog(x) = f(g(x)) = 3(2x) = 6x\\gof(x) = g(f(x)) = 2(3x) = 6x\end{array} \right.\\\\ \to fog(x) = gof(x)\end{array}\)
پ
درست
\(fog(4) = f(g(4)) = f(7) = 5\)
ت
درست
\(\left\{ \begin{array}{l}fog(5) = f(g(5)) = \sqrt {2 \times 5 - 1} = \sqrt 9 = 3\\g(2) = 2 \times 2 - 1 = 3\end{array} \right.\)
5 الناز می خواهد از فروشگاه بهار یک لپ تاپ با قیمت بیش از دو میلیون تومان خریداری نماید. این فروشگاه در ماه رمضان مسابقه ای برگزار کرده و به برندگان کارت تخفیف 20 درصدی داده است و الناز نیز در این مسابقه برنده شده است. همچنین این فروشگاه روزهای پنج شنبه به مشتریان خود در خریدهای بیش از یک و نیم میلیون تومان، 200 هزار تومان تخفیف نقدی می دهد. با استفاده از تابع مرکب نشان دهید کدام یک از حالت های الف یا ب به نفع الناز است؟
الف اول کارت تخفیف 20 درصدی و بعد تخفیف نقدی را استفاده کند.
ب اول تخفیف نقدی را استفاده کند و بعد کارت تخفیف را ارائه دهد.
الف
حالت الف مقرون به صرفه است؛ چرا که :
\(\begin{array}{l}\left\{ \begin{array}{l}f(x) = x - \frac{2}{{10}}x = \frac{8}{{10}}x = \frac{4}{5}x\quad (x > 0)\\g(x) = x - 200,000\quad (x > 1,500,000)\end{array} \right.\\\\ \to g(f(x)) = f(x) - 200,000 = \frac{4}{5}x - 200,000\\\\\frac{{80}}{{100}} \times 2,000,000 - 200,000 = 1,400,000\end{array}\)
ب
\(\begin{array}{l}f(g(x)) = f(x - 200,000) = \frac{4}{5}x - 160,000\\\frac{{80}}{{100}} \times (2,000,000 - 200,000) = 1,440,000\end{array}\)
6 تابع\(h\left( x \right) = {\left( {3{x^2} - 4x + 1} \right)^5}\) ترکیب کدام دو تابع زیر است؟
\(f\left( x \right) = \sqrt[5]{x}\;\;;\;\;g\left( x \right) = 3{x^2} - 4x + 1\) الف
\(k\left( x \right) = {x^5}\;\;;\;\;l\left( x \right) = 3{x^2} - 4x + 1\) ب
الف
\(\left\{ \begin{array}{l}fog(x) = f(g(x)) = \sqrt[5]{{3{x^2} - 4x + 1}}\quad \quad \to \quad \times \\gof(x) = g(f(x)) = 3\sqrt[5]{{{x^2}}} - 4\sqrt[5]{x} + 1\quad \to \quad \times \end{array} \right.\)
ب
\(\begin{array}{l}kol(x) = k(l(x)) = {(3{x^2} - 4x + 1)^5} = h(x)\\lok(x) = l(k(x)) = 3{({x^5})^2} - 4({x^5}) + 1\quad \quad \to \quad \times \end{array}\)
7 هریک از توابع زیر را به صورت ترکیب دو تابع بنویسید. آیا جواب منحصر به فرد است؟
\(h\left( x \right) = \sqrt[3]{{{x^2} + 1}}\) الف
\(l\left( x \right) = \sqrt {{x^2} + 5} \) ب
الف
\(h(x) = \sqrt[3]{{{x^2} + 1}} \to \left\{ \begin{array}{l}f(x) = {x^2} + 1\\g(x) = \sqrt[3]{x}\end{array} \right.\)
ب
\(l(x) = \sqrt {{x^2} + 5} \to \left\{ \begin{array}{l}f(x) = {x^2} + 5\\g(x) = \sqrt x \end{array} \right.\)
خیر؛ منحصر بفرد نیست.
8 با توجه به نمودارهای توابع f و g، مقادیر زیر را در صورت وجود بیابید.

الف \((fog)(-1)\)
ب \((gof)(0)\)
پ \((fog)(1)\)
ت \((gof)(-1)\)
الف
\(\left( {fog} \right)\left( { - 1} \right) = f(g( - 1)) = f( - 3) = 1\)
ب
\(\left( {gof} \right)\left( 0 \right) = g(f(0)) = g(2) = - 6\)
پ
\(\left( {fog} \right)\left( 1 \right) = f(g(1)) = f( - 5) = 3\)
ت
\(\left( {gof} \right)\left( { - 1} \right) = g(f( - 1)) = g(1) = - 5\)
9 با توجه به ضابطه های توابع f و g، معادلات مورد نظر را تشکیل داده و آنها را حل کنید.
\(f\left( x \right) = 2x - 5\;\;;\;\;g\left( x \right) = {x^2} - 3x + 8\;\;:\;\;\left( {fog} \right)\left( x \right) = 7\) الف
\(f\left( x \right) = 3{x^2} + x - 1\;\;;\;\;g\left( x \right) = 1 - 2x\;\;:\;\;\left( {gof} \right)\left( x \right) = - 5\) ب
الف
\(\begin{array}{l}f(g(x)) = 2({x^2} - 3x + 8) - 5 = 7\\\\ \Rightarrow 2{x^2} - 6x + 11 = 7 \Rightarrow 2{x^2} - 6x + 4 = 0\\\\ \to \Delta = {b^2} - 4ac = {( - 6)^2} - 4(2)(4) = 4\\\\ \Rightarrow x = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{6 \pm \sqrt 4 }}{4} \Rightarrow \left\{ \begin{array}{l}x = 1\\x = 2\end{array} \right.\end{array}\)
ب
\(\begin{array}{l}g(f(x)) = 1 - 2(3{x^2} + x - 1) = - 5 \Rightarrow - 6{x^2} - 2x + 3 = - 5\\\\ \Rightarrow - 6{x^2} - 2x + 8 = 0\\\\ \to \Delta = {b^2} - 4ac = {( - 2)^2} - 4( - 6)(8) = 196\\\\ \Rightarrow x = \frac{{ - b \pm \sqrt \Delta }}{{2a}} = \frac{{2 \pm \sqrt {196} }}{{ - 12}} \Rightarrow \left\{ \begin{array}{l}x = 1\\x = - \frac{4}{3}\end{array} \right.\end{array}\)
10 با استفاده از نمودار y=cosx، نمودار توابع زیر رسم شده است، ضابطه هر نمودار را مشخص کنید.
الف \(y = - \frac{1}{2}\cos \left( { - \frac{1}{2}x} \right)\)
ب \(y = 2\cos 2x\)
پ \(y = \cos \left( {\frac{1}{2}x} \right)\)
ت \(y = - \cos 2x\)
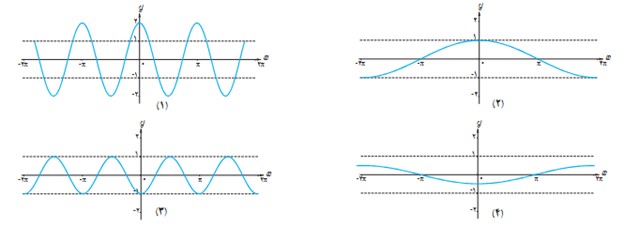
الف
4
ب
1
پ
2
ت
3
11 نمودار توابع \(y=-sin2x-1 \) و \(y = 2\sin \left( {\frac{{ - 1}}{3}x} \right)\) را به کمک نمودار تابع \(y=sinx\) در بازۀ \([-π,π]\) رسم کنید.

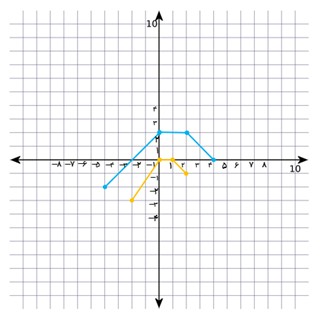
12 با استفاده از نمودار تابع f، نمودارهای خواسته شده را رسم کنید.

الف \(y = \frac{1}{2}f\left( {2x} \right) - 1\)
ب \(y = - f\left( { - x} \right) + 2\)
پ \(y = 2f\left( {x - 1} \right) - 3\)
ت \(y = 2f\left( {\frac{1}{2}x} \right)\)
الف
ب

پ
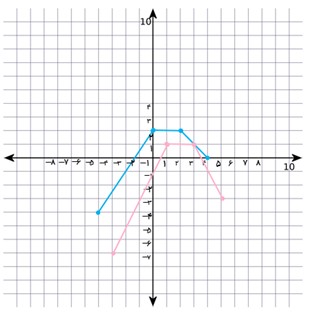
ت

مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















