1736019749.png)
گام به گام تمرین صفحه 29 درس 1 ریاضی دوازدهم تجربی (تابع)
تعداد بازدید : 59.96Mپاسخ تمرین صفحه 29 ریاضی دوازدهم تجربی
-گام به گام تمرین صفحه 29 درس تابع
-تمرین صفحه 29 درس 1
-1 ضابطهٔ تابع وارون توابع یک به یک زیر را به دست آورید.
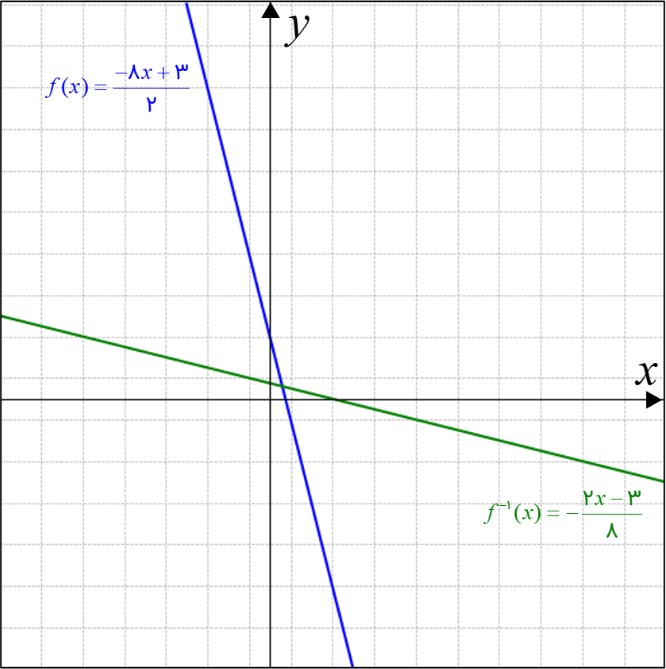
\(f(x) = \frac{{ - 8x + 3}}{2}\) الف
\(\begin{array}{l}y = f(x)\\\\ \Rightarrow y = \frac{{ - 8x + 3}}{2}\\\\ \Rightarrow 2y = - 8x + 3\\\\ \Rightarrow 2y - 3 = - 8x\\\\ \Rightarrow x = - \frac{{2y - 3}}{8} \Rightarrow \left\{ \begin{array}{l}x \to y\\\\y \to x\end{array} \right.\\\\ \Rightarrow y = - \frac{{2x - 3}}{8}\\\\ \Rightarrow {f^{ - 1}}(x) = - \frac{{2x - 3}}{8}\end{array}\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
قبل از اینکه تابع معکوس \(f(x)\) را بدست بیاریم، ابتدا بایستی ببینیم که یک به یک هست یا نه.
همگی توابع یک جمله ای، توابعی وارون پذیر می باشند.
اما بیایید بررسی کنیم، ببینیم که آیا تابع \(f(x)\) وارون پذیر هست یا خیر. برای بررسی کافی است که دو مقدار \(f({x_1})\) و \(f({x_2})\) را برابر هم قرار دهیم. بعد از ساده سازی، بایستی \({x_1} = {x_2}\) شود. در غیر این صورت تابع \(f(x)\) وارون پذیر نمی باشد. ابتدا بررسی لازم را انجام دهیم:
\(\begin{array}{l}f({x_1}) = f({x_2})\\\\ \Rightarrow \frac{{ - 8{x_1} + 3}}{2} = \frac{{ - 8{x_2} + 3}}{2}\\\\ \Rightarrow - 8{x_1} + 3 = - 8{x_2} + 3\\\\ \Rightarrow - 8{x_1} = - 8{x_2}\\\\ \Rightarrow {x_1} = {x_2}\end{array}\)
چون \({x_1} = {x_2}\) پس تابع \(f(x)\) وارون پذیر است و وارون آن را هم در بالا بدست آوردیم.
دامنه و برد توابع وارون:
دامنه تابع \(f(x)\) با برد تابع \({f^{ - 1}}(x)\) با هم مساوی است و برابر \(\mathbb{R}\) می باشد.
برد تابع \(f(x)\) با دامنه تابع \({f^{ - 1}}(x)\) با هم مساوی است و برابر \(\mathbb{R}\) می باشد.
در شکل زیر، نمودار هر دو تابع کشیده شده است.
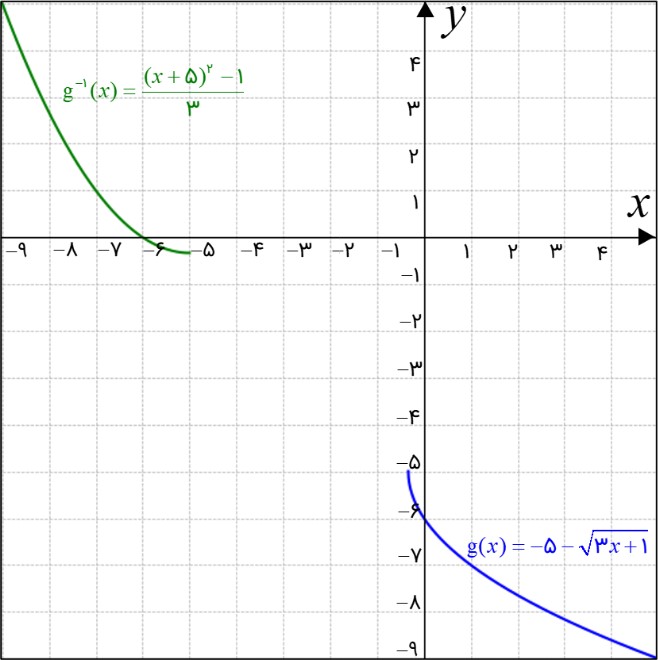
\(g(x) = - 5 - \sqrt {3x + 1} \) ب
\(\begin{array}{l}y = g(x)\\\\ \Rightarrow y = - 5 - \sqrt {3x + 1} \\\\ \Rightarrow y + 5 = - \sqrt {3x + 1} \\\\ \Rightarrow {(y + 5)^2} = 3x + 1\\\\ \Rightarrow 3x = {(y + 5)^2} - 1\\\\ \Rightarrow x = \frac{{{{(y + 5)}^2} - 1}}{3} \Rightarrow \left\{ \begin{array}{l}x \to y\\\\y \to x\end{array} \right.\\\\ \Rightarrow y = \frac{{{{(x + 5)}^2} - 1}}{3}\\\\ \Rightarrow {g^{ - 1}}(x) = \frac{{{{(x + 5)}^2} - 1}}{3}\end{array}\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
برای این قسمت هم بایستی بررسی کنیم ببینیم آیا تابع وارون پذیر هست یا خیر.
\(\begin{array}{l}g({x_1}) = g({x_2})\\\\ \Rightarrow - 5 - \sqrt {3{x_1} + 1} = - 5 - \sqrt {3{x_2} + 1} \\\\ \Rightarrow - \sqrt {3{x_1} + 1} = - \sqrt {3{x_2} + 1} \\\\ \Rightarrow \sqrt {3{x_1} + 1} = \sqrt {3{x_2} + 1} \\\\ \Rightarrow 3{x_1} + 1 = 3{x_2} + 1\\\\ \Rightarrow 3{x_1} = 3{x_2}\\\\ \Rightarrow {x_1} = {x_2}\end{array}\)
دامنه تابع \(g(x)\) با برد تابع \({g^{ - 1}}(x)\) با هم مساوی است و برابر \([ - \frac{1}{3}\,,\,\infty )\) می باشد. (چرا؟)
می دانیم که بایستی زیر رادیکال بزرگتر و مساوی با صفر باشد. پس برای اینکه دامنه تابع \(g(x)\) را بدست آوریم، کافی است که زیر رادیکال را بزرگتر و مساوی با صفر قرار دهیم. داریم:
\(\begin{array}{l}3x + 1 \ge 0\\\\ \Rightarrow 3x \ge - 1\\\\ \Rightarrow x \ge - \frac{1}{3}\\\\ \Rightarrow {D_g} = {R_{{g^{ - 1}}}} = [ - \frac{1}{3}\,,\,\infty )\end{array}\)
برد تابع \(f(x)\) با دامنه تابع \({f^{ - 1}}(x)\) با هم مساوی است و برابر \(( - \infty \,,\, - 5]\) می باشد. (چرا؟)
برای محاسبه برد، به صورت زیر عمل می کنیم:
\(\begin{array}{l}x \ge - \frac{1}{3}\\\\ \Rightarrow 3x \ge - 1\\\\ \Rightarrow 3x + 1 \ge 0\\\\ \Rightarrow \sqrt {3x + 1} \ge 0\\\\ \Rightarrow - \sqrt {3x + 1} \le 0\\\\ \Rightarrow - 5 - \sqrt {3x + 1} \le - 5\\\\ \Rightarrow {R_g} = {D_{{g^{ - 1}}}} = ( - \infty \,,\, - 5]\end{array}\)
در شکل زیر، نمودار هر دو تابع کشیده شده است.
2 در مورد هر یک از قسمت های زیر نشان دهید که f و g وارون یکدیگرند.
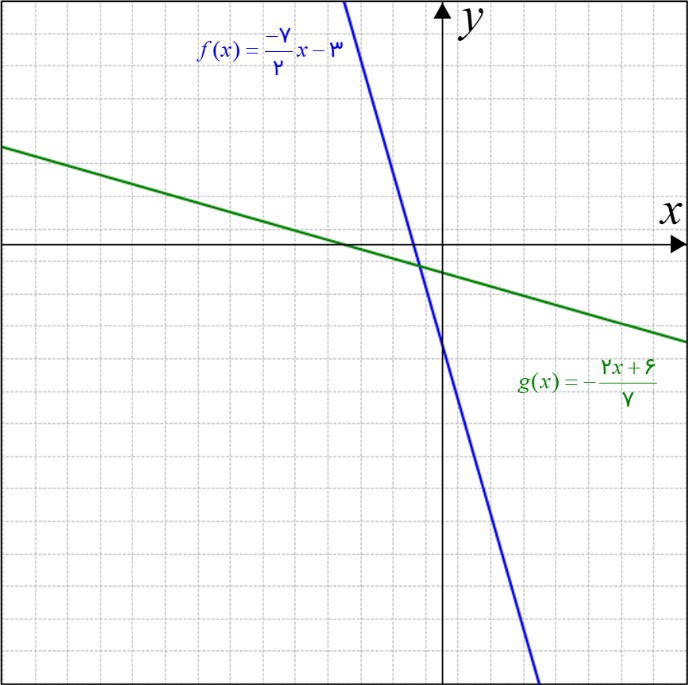
\(f(x) = \frac{{ - 7}}{2}x - 3\,\,\,\,\,,\,\,\,\,\,g(x) = - \frac{{2x + 6}}{7}\) الف
برای نشان دادن اینکه توابع f و g وارون یکدیگر هستند، کافی است که نشان دهیم نتیجه ترکیب این دو تابع در هم، همان تابع x می شود:
\(\begin{array}{l}fog(x) = f(g(x)) = f( - \frac{{2x + 6}}{7}) = \\\\\frac{{ - 7}}{2}( - \frac{{2x + 6}}{7}) - 3 = \frac{{2x + 6}}{2} - 3 = \\\\x + 3 - 3 = x\\\\gof(x) = g(f(x)) = g(\frac{{ - 7}}{2}x - 3) = \\\\ - \frac{{2(\frac{{ - 7}}{2}x - 3) + 6}}{7} = - \frac{{ - 7x - 6 + 6}}{7} = \\\\ - \frac{{ - 7x}}{7} = - ( - x) = x\end{array}\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
برای اینکه دو تابع وارون یکدیگر باشند، بایستی که نتیجه ترکیب این دو تابع برابر با تابع x شود. البته حتما در نظر داشته باشید که دامنه یکی از تابع ها برابر با برد تابع دیگری است و همچنین دامنه آن تابع نیز برابر با برد این تابع می باشد:
\(\begin{array}{l}\left\{ \begin{array}{l}f(x) = {g^{ - 1}}(x)\\\\g(x) = {f^{ - 1}}(x)\end{array} \right.\,\,\,\,\,\, \Rightarrow \,\,\,\,\,\left\{ \begin{array}{l}fog(x) = fo{f^{ - 1}}(x) = f({f^{ - 1}}(x)) = x\\\\gof(x) = go{g^{ - 1}}(x) = g({g^{ - 1}}(x)) = x\end{array} \right.\\\\\left\{ \begin{array}{l}{D_f} = {R_g} = \mathbb{R}\\\\{D_g} = {R_f} = \mathbb{R}\end{array} \right.\end{array}\)
در شکل زیر، نمودار هر دو تابع کشیده شده است.
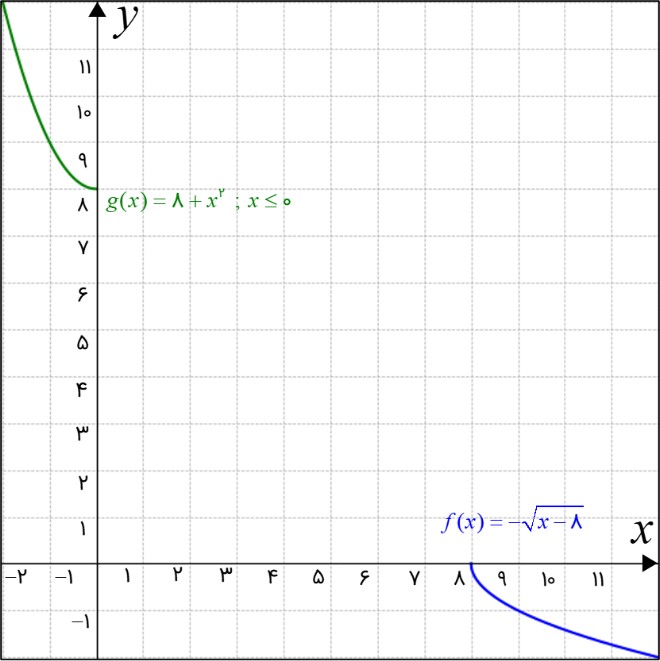
\(f(x) = - \sqrt {x - 8} \,\,\,\,\,,\,\,\,\,\,g(x) = 8 + {x^2}\,\,;\,\,x \le 0\) ب
برای این قسمت هم کافی است که مشابه قسمت الف عمل کنیم:
\(\begin{array}{l}f(x) = - \sqrt {x - 8} \,\,\,\,\,,\,\,\,\,\,g(x) = 8 + {x^2}\,\,;\,\,x \le 0\\\\fog(x) = f(g(x)) = f(8 + {x^2}) = \\\\ - \sqrt {(8 + {x^2}) - 8} = - \sqrt {{x^2}} = - \left| x \right| = - ( - x) = x\\\\gof(x) = g(f(x)) = g( - \sqrt {x - 8} ) = \\\\8 + {( - \sqrt {x - 8} )^2} = 8 + (x - 8) = x\end{array}\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
تنها توضیحی که بهتر هست در اینجا عرض کنیم این هست که وقتی fog(x) را محاسبه می کنیم، بهتر هست که یادمان باشد برای دامنه تابع g(x) داریم \(x \le 0\) ، پس به همین علت است که وقتی |x| را محاسبه می کنیم، آن را برابر با x– قرار می دهیم:
\(x \le 0 \Rightarrow \left| x \right| = - x\)
به این قسمت حتما توجه کنید!
در شکل زیر، نمودار هر دو تابع کشیده شده است.
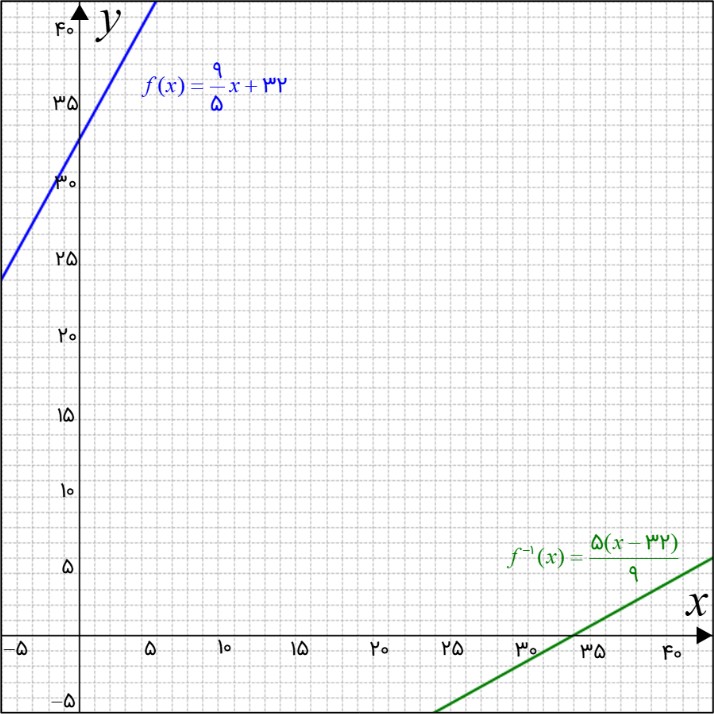
3 رابطهٔ بین درجهٔ سانتی گراد و فارنهایت که برای اندازه گیری دما استفاده می شوند به صورت \(f(x) = \frac{9}{5}x + 32\) است که در آن x میزان درجهٔ سانتی گراد و \(f(x)\) میزان درجهٔ فارنهایت است. \({f^{ - 1}}(x)\) را به دست آورده و توضیح دهید چه چیزی را نشان می دهد.
\(\begin{array}{l}y = f(x) = \frac{9}{5}x + 32\\\\y = f(x) \Rightarrow x = {f^{ - 1}}(y)\,\,\,\,\,(1)\\\\y = \frac{9}{5}x + 32 \Rightarrow y - 32 = \frac{9}{5}x\\\\ \Rightarrow x = \frac{{5(y - 32)}}{9}\,\,\,\,\,(2)\\\\(1)\,\,\,\,\,,\,\,\,\,\,(2) \Rightarrow \left\{ \begin{array}{l}x = {f^{ - 1}}(y)\\\\x = \frac{{5(y - 32)}}{9}\end{array} \right. \Rightarrow {f^{ - 1}}(y) = \frac{{5(y - 32)}}{9}\\\\ \Rightarrow {f^{ - 1}}(x) = \frac{{5(x - 32)}}{9}\end{array}\)
تابع \({f^{ - 1}}(x)\) ، مقدار درجه سانتی گراد را بر حسب درجه فارنهایت به ما می دهد.
توضیح تکمیلی (برای بهتر درک کردن مسئله):
روش حل این مسئله به این صورت هست که بایستی تابع معکوس آن را بدست بیاورید. روش حلی که برای بدست آوردن تابع معکوس استفاده شده، خیلی مرسوم هست:
اول از همه تابع \(f(x)\) را برابر y قرار می دهیم و از آنجا x را بر حسب y بدست می آوریم. در این صورت تساوی \(x = {f^{ - 1}}(y)\) بدست می آید. (شماره 1)
سپس تابع اصلی را که بر حسب x نوشته شده است را برابر y قرار می دهیم، یعنی \(y = \frac{9}{5}x + 32\) که بعد از ساده سازی دوباره x را بر حسب y بدست می آوریم که می شود \(x = \frac{{5(y - 32)}}{9}\) (شماره 2)
شماره های 1 و 2 را با هم برابر قرار می دهیم، چرا که هر دو برابر x هستند.
در نهایت کافی است که به جای y از متغیر x استفاده کنیم.
به این صورت تابع معکوس بدست می آید.
فقط دامنه و برد تابعی که می خواهید تابع معکوس آن را بدست آورید حتما در نظر داشته باشید. منظور مطمئن باشید که دامنه تابع معکوس با برد تابع اصلی و برد تابع معکوس با دامنه تابع اصلی برابر باشند.
\(\left\{ \begin{array}{l}{D_{{f^{ - f}}}} = {R_f}\\\\{R_{{f^{ - f}}}} = {D_f}\end{array} \right.\)
در شکل زیر، نمودار هر دو تابع کشیده شده است.
4 توابع زیر یک به یک نیستند. با محدود کردن دامنهٔ آنها توابعی یک به یک بسازید و ضابطهٔ وارون آنها را به دست آورید.
\(f(x) = \left| x \right|\) الف
\(\begin{array}{l}\left\{ \begin{array}{l}f(x) = \left| x \right|\\\\x \ge 0\end{array} \right. \Rightarrow f(x) = x\\\\y = f(x) = x\\\\y = f(x) \Rightarrow x = {f^{ - 1}}(y)\,\,\,\,\,(1)\\\\y = x \Rightarrow x = y\,\,\,\,\,(2)\\\\(1)\,\,\,\,\,,\,\,\,\,\,(2) \Rightarrow \left\{ \begin{array}{l}x = {f^{ - 1}}(y)\,\\\\x = y\end{array} \right. \Rightarrow {f^{ - 1}}(y) = y\\\\ \Rightarrow {f^{ - 1}}(x) = x\end{array}\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
بیایید تابع \(f(x) = \left| x \right|\) را رسم کنیم:
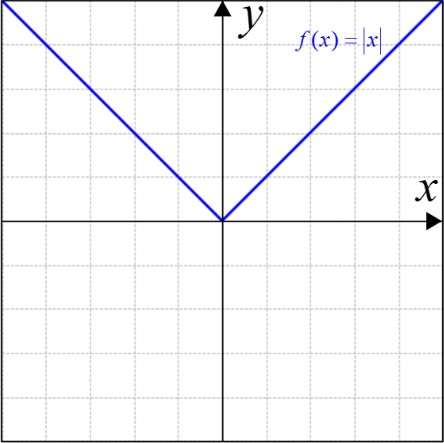
اگر نمودار جوابی که حل کردیم را بکشیم، تابع اصلی و معکوس آن یکی می شود:
\(\begin{array}{l}\left\{ \begin{array}{l}f(x) = \left| x \right|\\\\x \ge 0\end{array} \right. \Rightarrow f(x) = x\\\\{f^{ - 1}}(x) = x\,\,\,\,\,;\,\,\,\,\,x \ge 0\end{array}\)
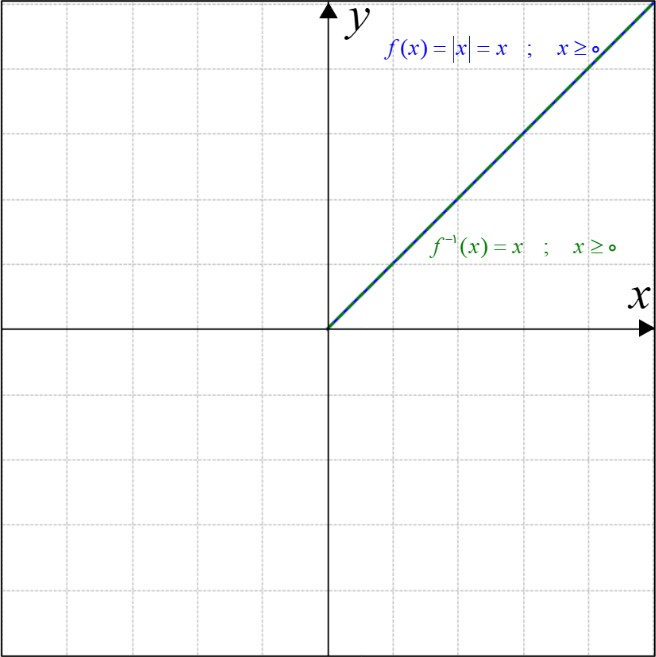
البته اگر \(x \le 0\) باشد، تابع اصلی و معکوس آن به صورت زیر می شود:
\(\begin{array}{l}\left\{ \begin{array}{l}f(x) = \left| x \right|\\\\x \le 0\end{array} \right. \Rightarrow f(x) = - x\\\\{f^{ - 1}}(x) = x\,\,\,\,\,;\,\,\,\,\,x \ge 0\end{array}\)
در شکل زیر، نمودار هر دو تابع کشیده شده است.
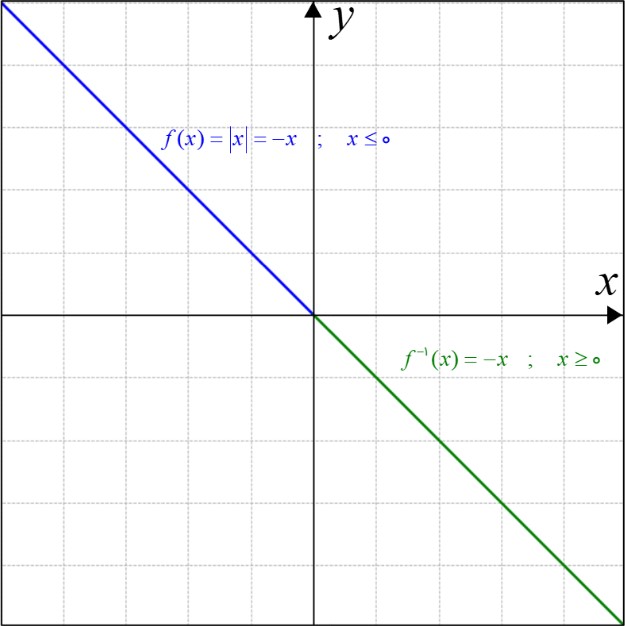
فقط دقت کنید که به این علت دامنه تابع معکوس \(x \ge 0\) شد که برد تابع اصلی تابع بزرگتر یا مساوی با صفر است:
\({D_{{f^{ - 1}}}} = {R_f} = \left[ {0\,,\,\infty } \right)\)
\(g(x) = - {x^2}\) ب
\(\begin{array}{l}\left\{ \begin{array}{l}g(x) = - {x^2}\\\\x \ge 0\,\,\,\,\,\,(1)\end{array} \right.\\\\y = g(x) = - {x^2}\\\\y = g(x) \Rightarrow x = {g^{ - 1}}(y)\,\,\,\,\,(2)\\\\y = - {x^2} \Rightarrow - y = {x^2}\\\\x = \pm \sqrt { - y} \\\\(1)\,\,\,\,\, \Rightarrow x = \sqrt { - y} \,\,\,\,\,(3)\\\\(2)\,\,\,\,\,,\,\,\,\,\,(3) \Rightarrow \left\{ \begin{array}{l}x = {g^{ - 1}}(y)\,\\\\x = \sqrt { - y} \end{array} \right. \Rightarrow {g^{ - 1}}(y) = \sqrt { - y} \\\\ \Rightarrow {g^{ - 1}}(x) = \sqrt { - x} \end{array}\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
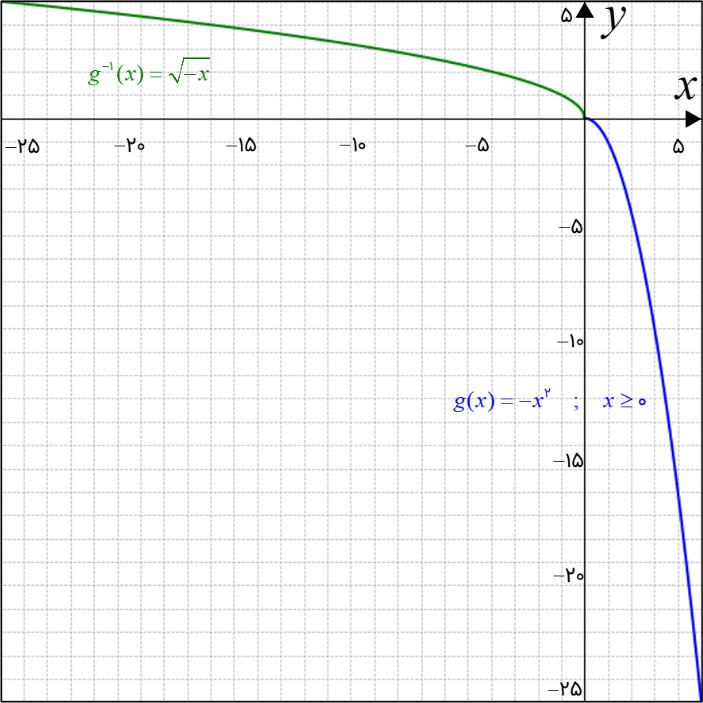
تابع \(g(x) = - {x^2}\) را بایستی در بازه \(x \ge 0\) بررسی کنیم. چرا که در این بازه، یک به یک و وارون پذیر می باشد. فقط بایستی در نظر داشته باشیم که در این بازه، نمودار این تابع در ناحیه چهارم محور مختصات قرار می گیرد. بنابراین معکوس این تابع در ناحیه دوم محور مختصات قرار می گیرد.
در شکل زیر نمودار تابع داده شده در مسئله با تابع معکوس آن کشیده شده است:
\(\begin{array}{l}\left\{ \begin{array}{l}g(x) = - {x^2}\\\\x \ge 0\end{array} \right.\\\\{g^{ - 1}}(x) = \sqrt { - x} \end{array}\)
البته اگر \(x \le 0\) باشد، تابع اصلی و معکوس آن به صورت زیر می شود:
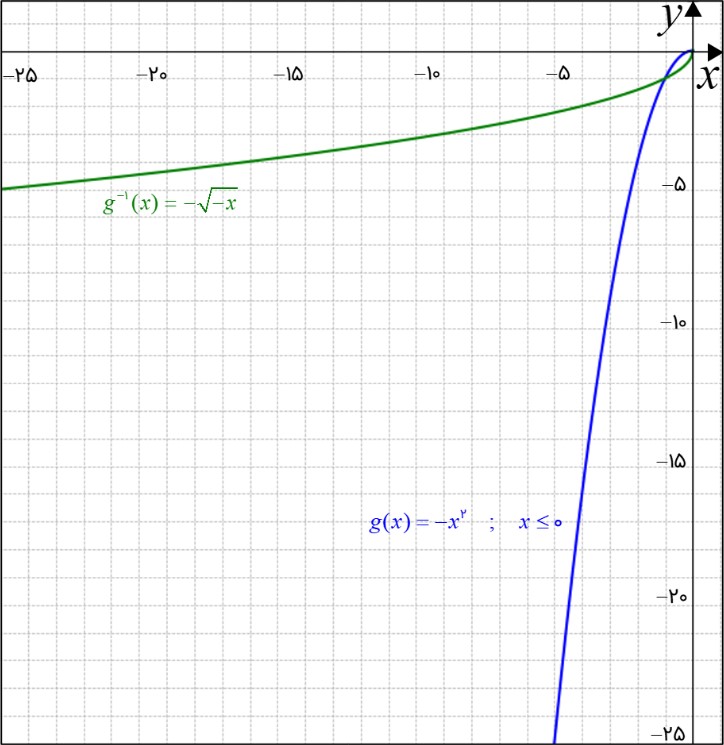
\(\begin{array}{l}\left\{ \begin{array}{l}g(x) = - {x^2}\\\\x \le 0\end{array} \right.\\\\{g^{ - 1}}(x) = - \sqrt { - x} \end{array}\)
در شکل زیر نمودار تابع داده شده در مسئله با تابع معکوس آن با توجه به بازه ی \(x \ge 0\) رسم شده است:
\(h(x) = {x^2} + 4x + 3\) پ
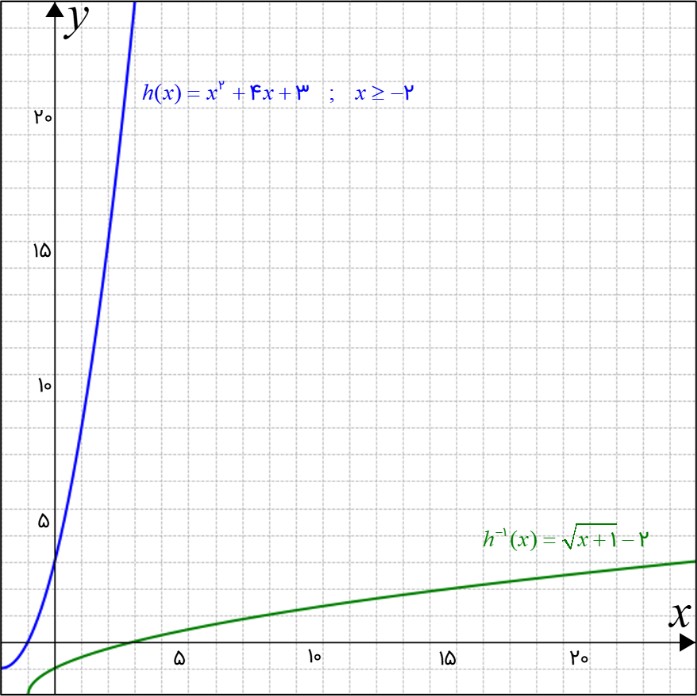
\(\begin{array}{l}h(x) = {x^2} + 4x + 3 = {(x + 2)^2} - 1\\\\\left\{ \begin{array}{l}h(x) = {(x + 2)^2} - 1\\\\x \ge - 2\,\,\,\,\,\,(1)\end{array} \right.\\\\y = h(x) = {(x + 2)^2} - 1\\\\y = h(x) \Rightarrow x = {h^{ - 1}}(y)\,\,\,\,\,(2)\\\\y = {(x + 2)^2} - 1 \Rightarrow y + 1 = {(x + 2)^2}\\\\ \Rightarrow x + 2 = \pm \sqrt {y + 1} \Rightarrow x = \pm \sqrt {y + 1} - 2\\\\(1)\,\,\,\,\, \Rightarrow x = \sqrt {y + 1} - 2\,\,\,\,\,(3)\\\\(2)\,\,\,\,\,,\,\,\,\,\,(3) \Rightarrow \left\{ \begin{array}{l}x = {h^{ - 1}}(y)\,\\\\\sqrt {y + 1} - 2\end{array} \right. \Rightarrow {h^{ - 1}}(y) = \sqrt {y + 1} - 2\\\\ \Rightarrow {h^{ - 1}}(x) = \sqrt {x + 1} - 2\end{array}\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
برای این تابع قبل از اینکه معکوس آن را بدست آوریم، بایستی آن را به صورت فرم مربع (توان دوم) در آوریم تا بتوانیم آن را تبدیل به تابع معکوس کنیم.
مربع کردن تابع چند جمله ای درجه 2:
برای مربع کردن تابع \(y = {x^2} + Bx + C\) ، ابتدا جمله ی \({(\frac{B}{2})^2}\) را با تابع جمع و تفریق می کنیم، سپس آن را به صورت زیر تبدیل به مربع می کنیم:
\(\begin{array}{l}y = {x^2} + Bx + C = {x^2} + Bx + {(\frac{B}{2})^2} + C - {(\frac{B}{2})^2}\\\\ \Rightarrow y = {(x - \frac{B}{2})^2} + (C - \frac{{{B^2}}}{4})\end{array}\)
سپس معکوس آن را بدست می آوریم.
فرم کلی مربع کردن تابع چند جمله ای درجه 2:
البته اگر تابع به فرم \(y = a{x^2} + bx + c\) باشد، به صورت درآوردن به فرم مربع، ابتدا از a فاکتور می گیریم تا ضریب عبارت \({x^2}\) ، برابر یک شود؛ یعنی به صورت زیر عمل می کنیم:
\(\begin{array}{l}y = a{x^2} + bx + c = a({x^2} + \frac{b}{a}x) + c = \\\\a({x^2} + \frac{b}{a}x + {(\frac{b}{{2a}})^2} - {(\frac{b}{{2a}})^2}) + c\\\\ \Rightarrow y = a({x^2} + \frac{b}{a}x + {(\frac{b}{{2a}})^2}) + (c - \frac{{{b^2}}}{{4a}})\end{array}\)
فقط این نکته را در نظر داشته باشید که چون تابع درجه 2 می باشد، در دو بازه ی جداگانه یک به یک خواهد بود. در جواب مسئله، فقط بازه ی \(\left[ { - 2\,,\,\infty } \right)\) در نظر گرفته شده است.
در شکل زیر نمودار تابع داده شده در مسئله با تابع معکوس آن کشیده شده است:
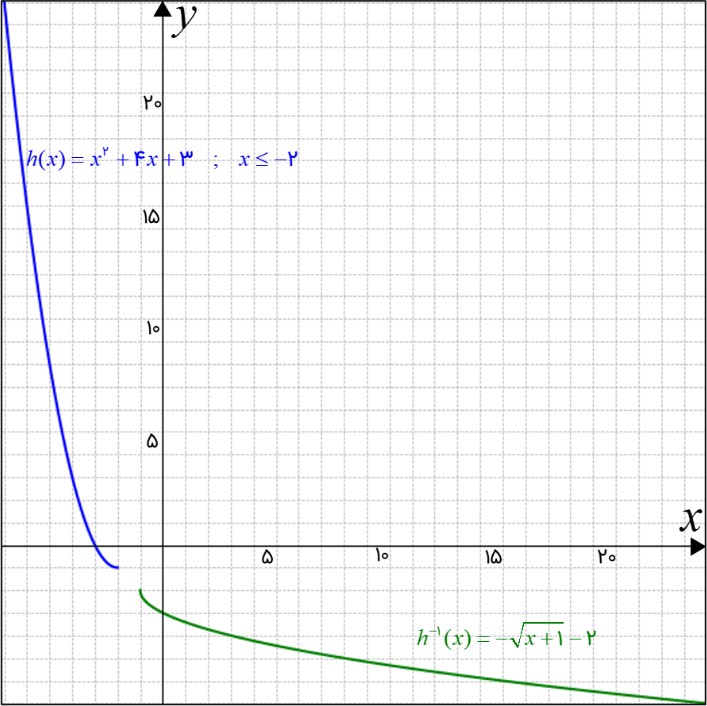
اگر دامنه را بازه \(\left( { - \infty \,,\, - 2} \right]\) در نظر بگیریم، انگاه تابع معکوس به صورت زیر می شود:
\(\begin{array}{l}\left\{ \begin{array}{l}h(x) = {x^2} + 4x + 3\\\\x \le - 2\end{array} \right.\\\\{h^{ - 1}}(x) = - \sqrt {x + 1} - 2\end{array}\)
در شکل زیر نمودار تابع داده شده در مسئله با تابع معکوس آن کشیده شده است:
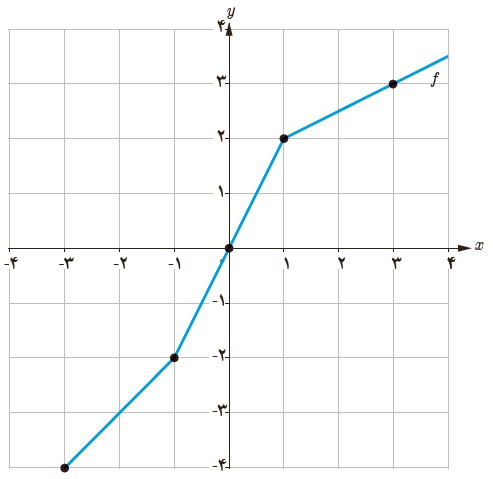
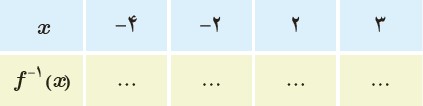
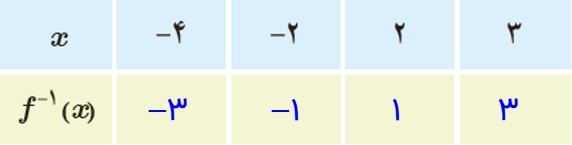
5 از نمودار تابع f برای تکمیل جدول استفاده کنید.
توضیح تکمیلی (برای بهتر درک کردن مسئله):
برای حل این جواب کافی است که نمودار تابع معکوس آن را بکشیم.
چطور وارون یک تابع را رسم کنیم؟
دو روش وجود دارد:
روش اول:
ابتدا خط y=x را رسم می کنیم و سپس قرینه این خطوط را نسبت به خط y=x می کشیم. نموداری که بدست می آید، تابع وارون تابع f می باشد.
روش دوم:
نقاط مشخص شده تابع f را می نویسیم. سپس در این مختصات نقاط کافی است که جای x ها را با y ها عوض کنیم. حال مختصات نقطه های جدید را روی نمودار معین می کنیم و نقطه ها را با خط به هم وصل می کنیم. نموداری که بدست می آید، تابع وارون تابع f می باشد.
در شکل زیر نمودار تابع وارون تابع f کشیده شده است:
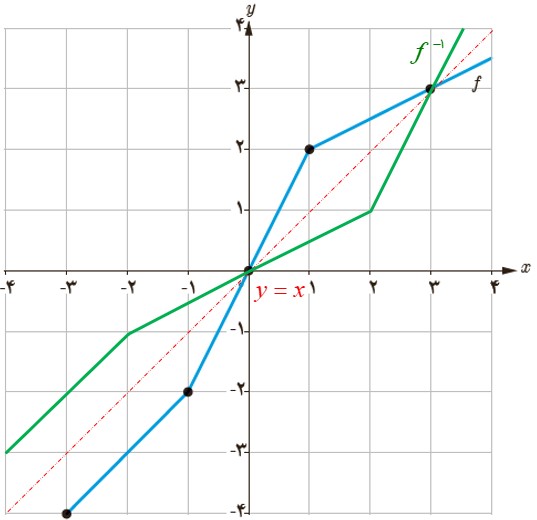
حال فقط کافی است که مقدار تابع \({f^{ - 1}}\) را به ازای x های داخل جدول داده شده در صورت مسئله بدست آوریم.
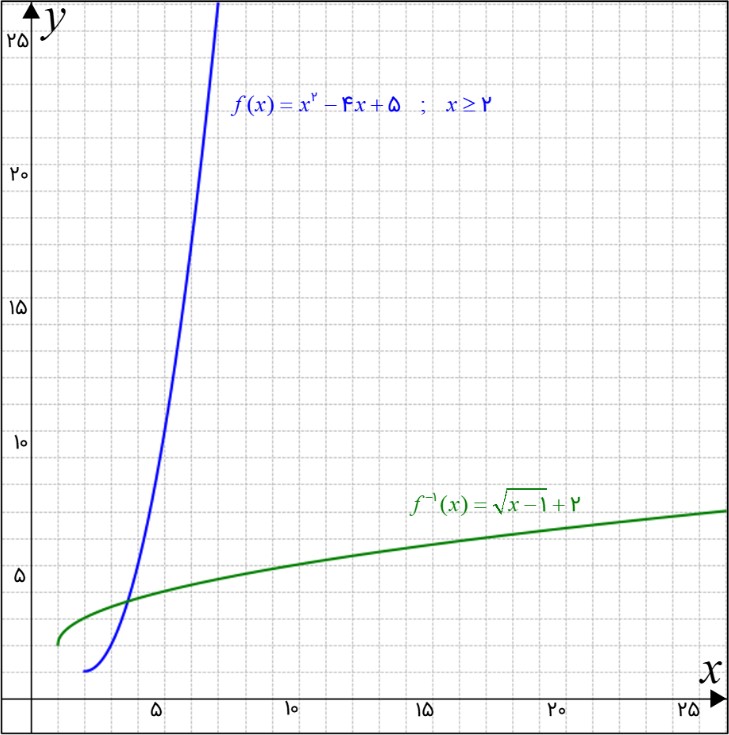
6 با محدود کردن دامنهٔ تابع \(f(x) = {x^2} - 4x + 5\) ، یک تابع یک به یک به دست آورده و دامنه و برد f و وارون آن را بنویسید و این دو تابع را رسم کنید.
\(\begin{array}{l}\left\{ \begin{array}{l}f(x) = {x^2} - 4x + 5 = {(x - 2)^2} + 1\\\\x \ge 2\,\,\,\,\,(1)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{D_f} = \left[ {2\,,\,\infty } \right)\\\\{R_f} = \left[ {1\,,\,\infty } \right)\end{array} \right.\\\\y = f(x) = {(x - 2)^2} + 1\\\\y = f(x) \Rightarrow x = {f^{ - 1}}(y)\,\,\,\,\,(2)\\\\y = {(x - 2)^2} + 1 \Rightarrow y - 1 = {(x - 2)^2}\\\\ \Rightarrow x - 2 = \pm \sqrt {y - 1} \Rightarrow x = \pm \sqrt {y - 1} + 2\\\\(1)\,\,\,\,\, \Rightarrow x = \sqrt {y - 1} + 2\,\,\,\,\,(3)\\\\(2)\,\,\,\,\,,\,\,\,\,\,(3) \Rightarrow {f^{ - 1}}(y) = \sqrt {y - 1} + 2\\\\ \Rightarrow {f^{ - 1}}(x) = \sqrt {x - 1} + 2 \Rightarrow \left\{ \begin{array}{l}{D_{{f^{ - 1}}}} = {R_f} = \left[ {1\,,\,\infty } \right)\\\\{R_{{f^{ - 1}}}} = {D_f} = \left[ {2\,,\,\infty } \right)\end{array} \right.\end{array}\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
تابع f را با توجه به آنچه در توضیح تکمیلی جواب مسئله 4 قسمت پ گفتیم، ابتدا به فرم تابع مربع در می آوریم، سپس معکوس آن را بدست می آوریم. البته این مسئله برای بازه \(\left[ {2\,,\,\infty } \right)\) حل شده است.
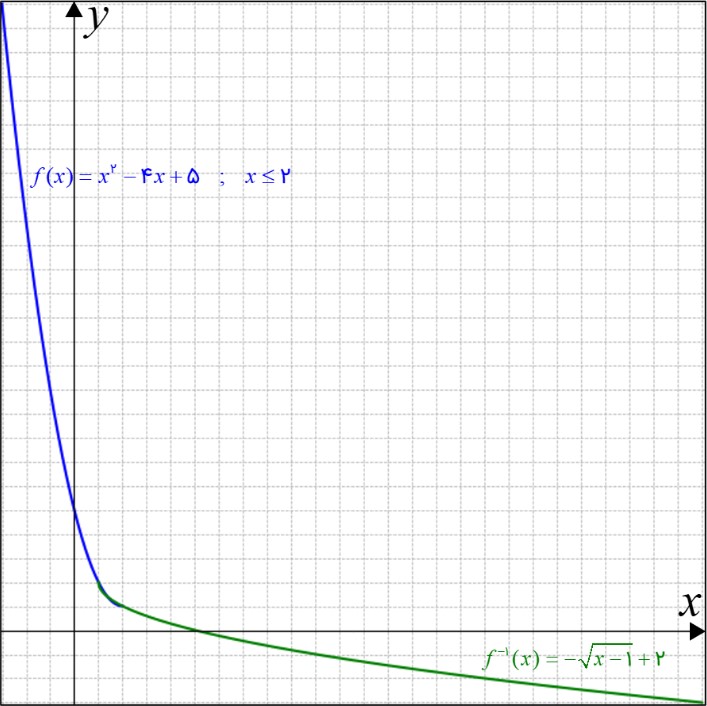
اگر بخواهیم همین مسئله را برای بازه \(\left( { - \infty \,,\,2} \right]\) حل کنیم، تابع معکوس آن به صورت زیر می شود:
\(\begin{array}{l}\left\{ \begin{array}{l}h(x) = {x^2} - 4x + 5\\\\x \le 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{D_f} = \left( { - \infty \,,\,2} \right]\\\\{R_f} = \left[ {1\,,\,\infty } \right)\end{array} \right.\\\\{f^{ - 1}}(x) = - \sqrt {x - 1} + 2 \Rightarrow \left\{ \begin{array}{l}{D_{{f^{ - 1}}}} = {R_f} = \left[ {1\,,\,\infty } \right)\\\\{R_{{f^{ - 1}}}} = {D_f} = \left( { - \infty \,,\,2} \right]\end{array} \right.\end{array}\)
در شکل زیر نمودار تابع داده شده در مسئله با تابع معکوس آن کشیده شده است:
7 اگر \(f(x) = \frac{1}{8}x - 3\) و \(g(x) = {x^3}\) ، مقادیر زیر را به دست آورید.
\({(fog)^{ - 1}}(5)\) الف
\(\begin{array}{l}{(fog)^{ - 1}}(5) = a\\\\ \Rightarrow fog(a) = 5\\\\ \Rightarrow f(g(a)) = 5\\\\ \Rightarrow f({a^3}) = 5\\\\ \Rightarrow \frac{1}{8}{a^3} - 3 = 5\\\\ \Rightarrow \frac{1}{8}{a^3} = 8\\\\ \Rightarrow {a^3} = 64\\\\ \Rightarrow a = \sqrt[3]{{64}} = 4\\\\ \Rightarrow {(fog)^{ - 1}}(5) = 4\end{array}\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
می دانیم که اگر داشته باشیم \(f\left( a \right) = b\) ، آنگاه \({f^{ - 1}}\left( b \right) = a\) . حال به جای تابع f ، تابع fog را داریم.
پس داریم:
\({(fog)^{ - 1}}(5) = a \Rightarrow fog(a) = 5\)
از آنجا هم تابع fog را بر حسب توابع f و g بدست آوردیم و مسئله را حل کردیم.
روش دیگر:
در روش دیگر، تابع fog را بدست آورده و سپس وارون آن را بدست می آوریم:
\(\begin{array}{l}\left\{ \begin{array}{l}f(x) = \frac{1}{8}x - 3\\\\g(x) = {x^3}\end{array} \right. \Rightarrow fog(x) = f(g(x)) = f({x^3}) = \frac{1}{8}{x^3} - 3\\\\y = fog(x) = \frac{1}{8}{x^3} - 3\\\\y = fog(x) \Rightarrow x = {(fog)^{ - 1}}(y)\,\,\,\,\,(1)\\\\y = \frac{1}{8}{x^3} - 3 \Rightarrow y + 3 = \frac{1}{8}{x^3} \Rightarrow {x^3} = 8(y + 3)\\\\ \Rightarrow x = \sqrt[3]{{8(y + 3)}}\,\,\,\,\,(2)\\\\(1)\,\,\,\,\,,\,\,\,\,\,(2) \Rightarrow {(fog)^{ - 1}}(y) = \sqrt[3]{{8(y + 3)}}\\\\ \Rightarrow {(fog)^{ - 1}}(x) = \sqrt[3]{{8(x + 3)}}\end{array}\)
حال کافی است که به جای x ، مقدار 5 را جایگذاری کرده و محاسبه نماییم:
\({(fog)^{ - 1}}(5) = \sqrt[3]{{8(5 + 3)}} = \sqrt[3]{{8 \times 8}} = \sqrt[3]{{64}} = 4\)
\(({f^{ - 1}}o{f^{ - 1}})(6)\) ب
برای حل این مسئله تنها راه این است که وارون تابع f را بدست آوریم و سپس با همان ترکیب کرده و سپس مقدار 6 را جایگذاری کرده و محاسبه نماییم:
\(\begin{array}{l}y = f(x) = \frac{1}{8}x - 3\\\\y = f(x) \Rightarrow x = {f^{ - 1}}(y)\,\,\,\,\,(1)\\\\y = \frac{1}{8}x - 3 \Rightarrow y + 3 = \frac{1}{8}x \Rightarrow x = 8(y + 3)\,\,\,\,\,(2)\\\\(1)\,\,\,\,\,,\,\,\,\,\,(2) \Rightarrow {f^{ - 1}}(y)\, = 8(y + 3)\\\\ \Rightarrow {f^{ - 1}}(x)\, = 8(x + 3) = 8x + 24\\\\{f^{ - 1}}o{f^{ - 1}}(x) = {f^{ - 1}}({f^{ - 1}}(x)\,) = {f^{ - 1}}(8x + 24)\, = \\\\8(8x + 24) + 24 = 64x + 192 + 24\\\\ \Rightarrow {f^{ - 1}}o{f^{ - 1}}(x) = 64x + 216\\\\{f^{ - 1}}o{f^{ - 1}}(6) = 64(6) + 216 = 384 + 216 = 600\end{array}\)
\(({g^{ - 1}}o{f^{ - 1}})(5)\) پ
برای حل این مسئله می توانیم وارون (معکوس) توابع f و g را بدست آورده، در یکدیگر ترکیب کرده و تابع مورد نظر را بدست بیاوریم و در نهایت مقدار 5 را در آن جایگذاری کرده و محاسبه نماییم:
\(\begin{array}{l}{f^{ - 1}}(x)\, = 8x + 24\,\,\,\,\,(1)\\\\g(x) = {x^3} \Rightarrow y = g(x) = {x^3}\\\\y = g(x) \Rightarrow x = {g^{ - 1}}(y)\,\,\,\,\,(2)\\\\y = {x^3} \Rightarrow x = \sqrt[3]{y}\,\,\,\,\,(3)\\\\(2)\,\,\,\,\,,\,\,\,\,\,(3) \Rightarrow {g^{ - 1}}(y)\, = \sqrt[3]{y}\\\\{g^{ - 1}}(x)\, = \sqrt[3]{x}\,\,\,\,\,\,(4)\\\\{g^{ - 1}}o{f^{ - 1}}(5)\, = {g^{ - 1}}({f^{ - 1}}(5)\,) = {g^{ - 1}}(8(5) + 24) = {g^{ - 1}}(64) = \\\\\sqrt[3]{{64}} = 4\end{array}\)
توضیح تکمیلی (برای بهتر درک کردن مسئله):
روش دیگری برای حل این مسئله هست که در قالب فرمول آمده است:
وارون ترکیب دو تابع:
برای دو تابع وارون پذیر (معکوس پذیر) f و g، همواره رابطه زیر برقرار است:
\({(fog)^{ - 1}}(x) = {g^{ - 1}}o{f^{ - 1}}(x)\)
حال کافی است که از این فرمول استفاده کنیم:
\(({g^{ - 1}}o{f^{ - 1}})(5) = {(fog)^{ - 1}}(5) = 4\)
مقدار آن در قسمت الف محاسبه شده است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
