جواب تمرین صفحه 52 درس 2 حسابان یازدهم (تابع)
تعداد بازدید : 81.09Mپاسخ تمرین صفحه 52 حسابان یازدهم
-گام به گام تمرین صفحه 52 درس تابع
-تمرین صفحه 52 درس 2
-شما در حال مشاهده جواب تمرین صفحه 52 حسابان یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 دامنهٔ توابع زیر را بیابید.
الف \(f\left( x \right) = \frac{{x - 1}}{{2 - x}}\)
ب \(f\left( x \right) = \frac{{ - 3x}}{{{x^2} + 1}}\)
پ \(f\left( x \right) = \frac{{2x + 3}}{{{x^2} + x - 12}}\)
ت \(f\left( x \right) = \sqrt {3x + 1}\)
ث \(f\left( x \right) = 2\sqrt x - 3\)
ج \(f\left( x \right) = \sqrt {8 - x}\)
الف \({D_f} = \mathbb{R} - \left\{ 2 \right\}\)
ب \({D_f} = \mathbb{R}\)
پ \({D_f} = \mathbb{R} - \left\{ { - 4\;,\;3} \right\}\)
ت \({D_f} = \left[ { - \frac{1}{3}\;,\;\infty } \right)\)
ث \({D_f} = \left[ {0\;,\;\infty } \right)\)
ج \({D_f} = \left( { - \infty \;,\;8} \right]\)
2 توضیح دهید که چگونه با استفاده از نمودار تابع \(f\left( x \right) = \frac{1}{x}\) می توان نمودار تابع \(g\left( x \right) = - \frac{1}{x}\) را رسم کرد.
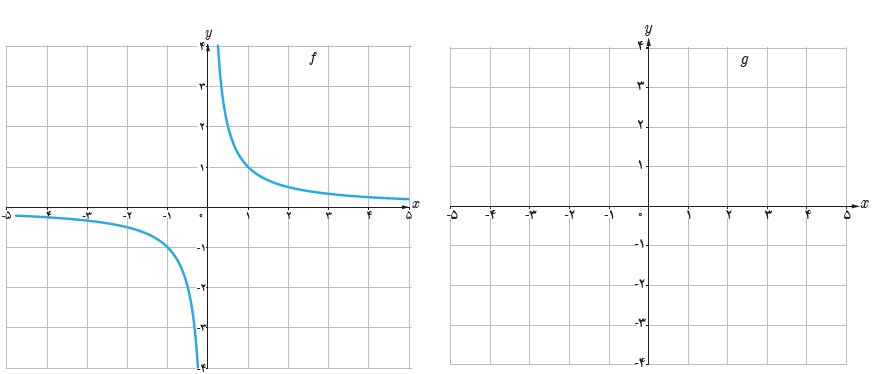
با قرینه کردن تابع f نسبت به محور x ، تابع g بدست می آید:
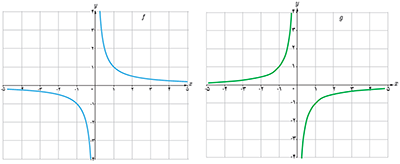
3 نمودار تابع \(y = - \sqrt x \) را با استفاده از نمودار تابع \(y = \sqrt x \) رسم کنید.
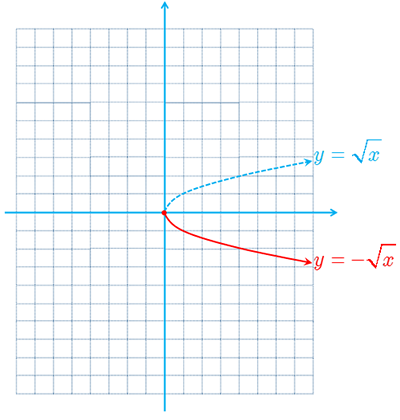
4 نمودار توابع زیر را رسم نموده و دامنه و برد هر یک را معلوم کنید.
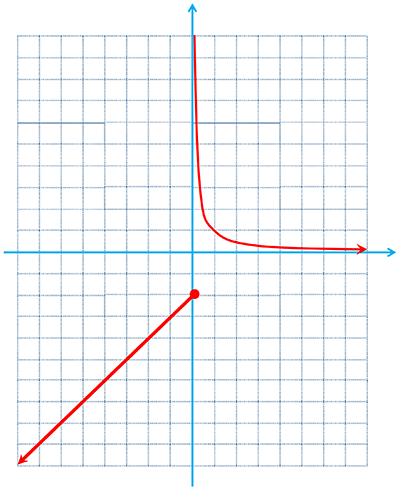
الف \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}\begin{array}{l}\frac{1}{x}\;\;\;\;\;\;\;\;\;\;x \ge 0\\\end{array}\\{x - 2\;\;\;\;\;\;x \le 0}\end{array}} \right.\)
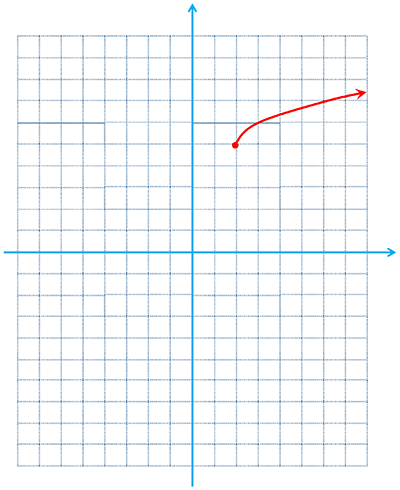
ب \(f\left( x \right) = \sqrt {x - 2} + 5\)
پ \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\sqrt x + 2\:\,\,\,\,\:\:\:\:\:\:\:\:\:x > 0}\end{array}}\\{\sqrt {x + 2} \:\:\:\:\:\: - 2 \le x \le 0}\end{array}} \right.\)
ت \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{ - \frac{1}{x}\,\,\,\,\:\:\:\:\:\:\:\:\:x > 0}\end{array}}\\{ - \sqrt x \:\:\:\:\,\,\,\,\,\,\,\,\:x \ge 0}\end{array}} \right.\)
الف
\(\left\{ \begin{array}{l}{D_f} = \mathbb{R}\\{R_f} = \left( { - \;\infty \;,\; - 2} \right]\; \cup \left( {0\;,\; + \infty } \right)\end{array} \right.\)
ب
\(\left\{ \begin{array}{l}{D_f} = \left[ {2\;,\; + \infty } \right)\\{R_f} = \left[ {5\;,\; + \infty } \right)\end{array} \right.\)
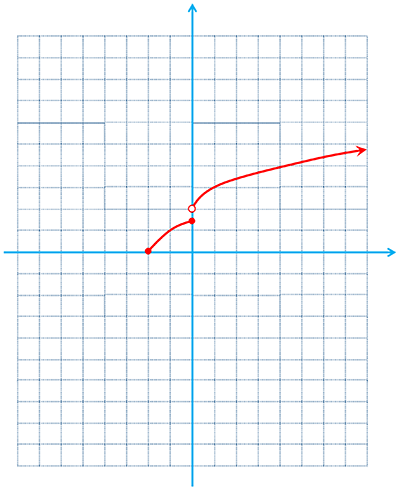
پ
\(\left\{ \begin{array}{l}{D_f} = \left[ { - 2\;,\; + \infty } \right)\\{R_f} = \left[ {0\;,\;\sqrt 2 } \right]\; \cup \left( {0\;,\;2} \right)\end{array} \right.\)
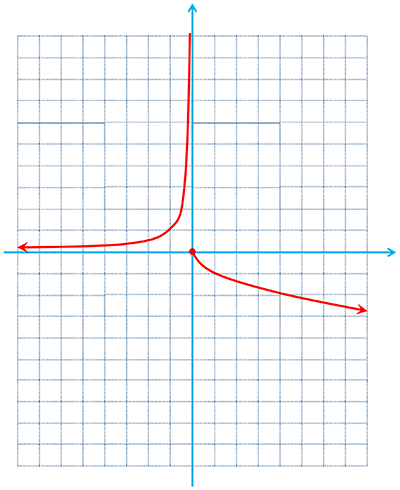
ت
\(\left\{ \begin{array}{l}{D_f} = \mathbb{R}\\{R_f} = \mathbb{R}\end{array} \right.\)
5 کدام یک از معادلات زیر یک تابع را مشخص می کند؟
الف \(3x + 2y = 12\)
ب x = 1
پ y = -2
ت \(f\left( x \right) = \left\{ \begin{array}{l}x + 3\;\;\;\;x \le 0\\x - 1\;\;\;\;\;x > 0\end{array} \right.\)
ث y2 = x2
ج y = |x|
الف تابع است.
ب تابع نیست.
پ تابع است.
ت تابع نیست.
ث تابع نیست.
ج تابع است.
6 هزینه پاک سازی x درصد از آلودگی های شهری و صنعتی از رودخانه ای، به وسیله تابع \(f\left( x \right) = \frac{{255x}}{{100 - x}}\) محاسبه می شود که در آن x درصد آلودگی و f(x) هزینه پاک سازی برحسب میلیون تومان است..
الف هزینه پاک سازی 50% از آلودگی این رودخانه چقدر است؟
ب دامنه این تابع در این حالت (واقعی) را به کمک یک بازه نمایش دهید.
الف
\(\begin{array}{l}f\left( x \right) = \frac{{255x}}{{100 - x}} \Rightarrow x = 50\\\\ \Rightarrow f\left( {50} \right) = \frac{{255\left( {50} \right)}}{{100 - 50}} = 255\end{array}\)
255 میلیون تومان
ب
\({D_f} = \left[ {0\;,\;100} \right)\)
7 نمودار تابع های زیر را رسم کنید.
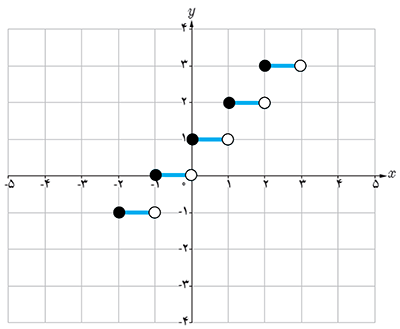
الف \(f\left( x \right) = \left[ x \right] + 1\;\;\;,\;\;\; - 2 \le x < 3\)
ب \(f\left( x \right) = \left[ {\frac{1}{2}x} \right]\;\;\;,\;\;\; - 4 \le x \le 4\)
الف
\(\begin{array}{l} - 2 \le x < - 1 \Rightarrow \left[ x \right] = - 2 \Rightarrow f\left( x \right) = - 2 + 1 = - 1\\ - 1 \le x < 0 \Rightarrow \left[ x \right] = - 1 \Rightarrow f\left( x \right) = - 1 + 1 = 0\\0 \le x < 1 \Rightarrow \left[ x \right] = 0 \Rightarrow f\left( x \right) = 0 + 1 = 1\\1 \le x < 2 \Rightarrow \left[ x \right] = 1 \Rightarrow f\left( x \right) = 1 + 1 = 2\\2 \le x < 3 \Rightarrow \left[ x \right] = 2 \Rightarrow f\left( x \right) = 2 + 1 = 3\end{array}\)
ب
\(\begin{array}{l} - 2 \le x < - 1 \Rightarrow \left[ x \right] = - 2 \Rightarrow f\left( x \right) = - 2 + 1 = - 1\\ - 1 \le x < 0 \Rightarrow \left[ x \right] = - 1 \Rightarrow f\left( x \right) = - 1 + 1 = 0\\0 \le x < 1 \Rightarrow \left[ x \right] = 0 \Rightarrow f\left( x \right) = 0 + 1 = 1\\1 \le x < 2 \Rightarrow \left[ x \right] = 1 \Rightarrow f\left( x \right) = 1 + 1 = 2\\2 \le x < 3 \Rightarrow \left[ x \right] = 2 \Rightarrow f\left( x \right) = 2 + 1 = 3\end{array}\)
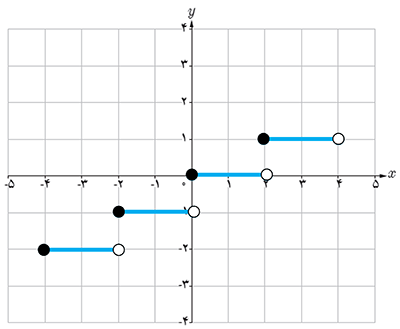
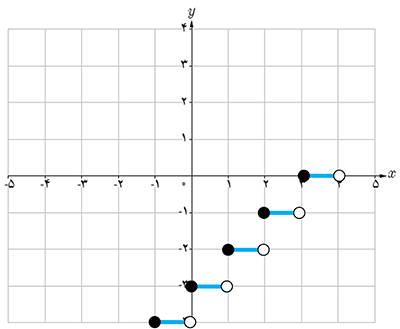
8 نمودارهای دو تابع y=[x-3] و y=[x]-3 را در یک دستگاه مختصات رسم کنید. چه رابطه ای بین این دو تابع وجود دارد؟
\(\begin{array}{l}y = \left[ x \right] - 3\\ - 1 \le x < 0 \Rightarrow \left[ x \right] = - 1 \Rightarrow f\left( x \right) = - 4\\0 \le x < 1 \Rightarrow \left[ x \right] = 0 \Rightarrow f\left( x \right) = - 3\\1 \le x < 2 \Rightarrow \left[ x \right] = 1 \Rightarrow f\left( x \right) = - 2\\2 \le x < 3 \Rightarrow \left[ x \right] = 2 \Rightarrow f\left( x \right) = - 1\\3 \le x < 4 \Rightarrow \left[ x \right] = 3 \Rightarrow f\left( x \right) = 0\\\\y = \left[ {x - 3} \right]\\ - 1 \le x < 0 \Rightarrow - 4 \le x - 3 < - 3 \Rightarrow \left[ {x - 3} \right] = - 4 \Rightarrow f\left( x \right) = - 4\\0 \le x < 1 \Rightarrow - 3 \le x - 3 < - 2 \Rightarrow \left[ {x - 3} \right] = - 3 \Rightarrow f\left( x \right) = - 3\\1 \le x < 2 \Rightarrow - 2 \le x - 3 < - 1 \Rightarrow \left[ {x - 3} \right] = - 2 \Rightarrow f\left( x \right) = - 2\\2 \le x < 3 \Rightarrow - 1 \le x - 3 < 0 \Rightarrow \left[ {x - 3} \right] = - 1 \Rightarrow f\left( x \right) = - 1\\3 \le x < 4 \Rightarrow 0 \le x - 3 < 1 \Rightarrow \left[ {x - 3} \right] = 0 \Rightarrow f\left( x \right) = 0\end{array}\)
این دو تابع با هم برابرند.
9 اگر تعداد افرادی که،طی یک مدت معین، به وسیله یک نوع ویروس آلوده می شوند با دستور \(n\left( t \right) = \frac{{9500t - 2000}}{{4 + t}}\) به دست آید که در آن t>0 زمان برحسب ماه است:
الف تعداد افرادی که در انتهای ماه پنجم آلوده شده اند چقدر است؟
ب پس از چند ماه تعداد افراد آلوده به 5500 نفر خواهد رسید؟
الف
\(\begin{array}{l}n\left( t \right) = \frac{{9500t - 2000}}{{4 + t}} \Rightarrow \\n\left( 5 \right) = \frac{{9500\left( 5 \right) - 2000}}{{4 + 5}} = \left[ {5055/\bar 5} \right] = 5055\end{array}\)
ب
\(\begin{array}{l}n\left( t \right) = \frac{{9500t - 2000}}{{4 + t}} \Rightarrow 5500 = \frac{{9500t - 2000}}{{4 + t}} \Rightarrow \\22000 + 5500t = 9500t - 2000\\ \Rightarrow 4000t = 24000 \Rightarrow t = 6\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















