جواب فعالیت صفحه 57 درس 2 حسابان یازدهم (تابع)
تعداد بازدید : 80.73Mپاسخ فعالیت صفحه 57 حسابان یازدهم
-گام به گام فعالیت صفحه 57 درس تابع
-فعالیت صفحه 57 درس 2
-شما در حال مشاهده جواب فعالیت صفحه 57 حسابان یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
تابع \(\left\{ \begin{array}{l}f:R \to R\\f\left( x \right) = 2x + 5\end{array} \right.\) را در نظر می گیریم.
الف به کمک نمودار f توضیح دهید که چرا f یک به یک است.
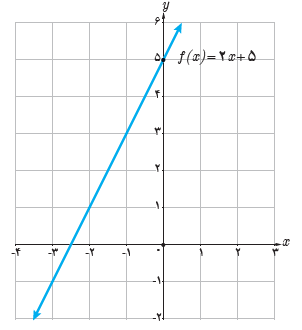
ب نمودار روبه رو را توضیح دهید:
\(\left( {11,3} \right) \in {f^{ - 1}}\) و \(\left( {3,11} \right) \in f\)
به عبارت دیگر f(3)=11 و f-1(11)=3
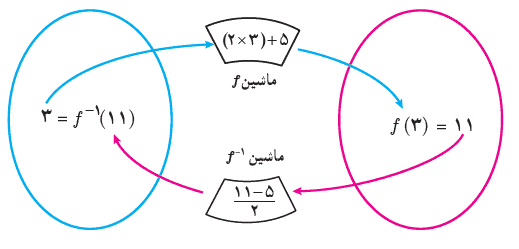
پ در حالت کلی برای هر عنصر \(x \in {D_f}\) ، نمودار مقابل را مانند ب کامل کنید.
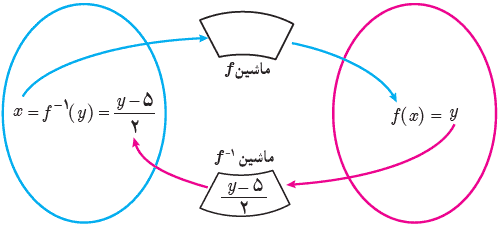
ت بنابراین می توان نوشت:
\(\begin{array}{l}f\left( x \right) = 2x + 5\;\;\;\;\;\left( {x \in {D_f}} \right)\\{f^{ - 1}}\left( y \right) = \frac{{y - 5}}{2}\;\;\;\;\left( {y \in {R_f}} \right)\end{array}\)
f-1 را به صورت های دیگری هم می توانیم نمایش دهیم. یک نمایش دیگر را بنویسید:
\(\begin{array}{l}\left\{ \begin{array}{l}{f^{ - 1}}:R \to R\\{f^{ - 1}}\left( y \right) = \frac{{y - 5}}{2}\end{array} \right.\\\\\left\{ \begin{array}{l}{f^{ - 1}}:R \to R\\{f^{ - 1}}\left( t \right) = \frac{{t - 5}}{2}\end{array} \right.\\\\\left\{ \begin{array}{l}{f^{ - 1}}:R \to R\\................\end{array} \right.\end{array}\)
آنچه که اهمیت دارد این است که دامنه f-1 همان برد f است. بنابراین یک نمایش مناسب برای f-1 به صورت زیر است:
\(\left\{ \begin{array}{l}{f^{ - 1}}:R \to R\\{f^{ - 1}}\left( x \right) = \frac{{x - 5}}{2}\end{array} \right.\)
عملیات به دست آوردن f-1 را به کمک نمودارهای صفحه قبل توضیح دهید.
\(\begin{array}{l}f\left( x \right) = 2x + 5\;\; \Rightarrow \;\;y = 2x + 5\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \Rightarrow \;\;2x = y - 5\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \Rightarrow \;\;x = \frac{{y - 5}}{2}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \Rightarrow \;\;{f^{ - 1}}\left( y \right) = \frac{{y - 5}}{2}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \Rightarrow \;\;{f^{ - 1}}\left( x \right) = \frac{{x - 5}}{2}\end{array}\)
الف چون هر خط افقی تابع را فقط در یک نقطه قطع می کند و همچنین هر عضو از دامنه فقط به یک عضو از برد نظیر شده است.
ب شکل رو به رو، دامنه f را گرفته و توسط ماشین f، آن را به برد f تبدیل می کند. برعکس همین عمل توسط ماشین معکوس f یا f-1 انجام می گیرد.
پ
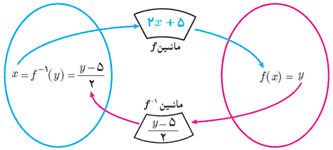
ت
\(\begin{array}{l}\left\{ \begin{array}{l}{f^{ - 1}}:R \to R\\{f^{ - 1}}\left( y \right) = \frac{{y - 5}}{2}\end{array} \right.\\\\\left\{ \begin{array}{l}{f^{ - 1}}:R \to R\\{f^{ - 1}}\left( t \right) = \frac{{t - 5}}{2}\end{array} \right.\\\\\left\{ \begin{array}{l}{f^{ - 1}}:R \to R\\{f^{ - 1}}\left( a \right) = \frac{{a - 5}}{2}\end{array} \right.\end{array}\)
ابتدا x را بر y بدست می آوریم. رابطه ای که بدست می آید، تابع معکوس f است ولی بر حسب متغیر y. در نتیجه به جای y، x را جای گذاری می کنیم. تابع بدست آمده، معکوس f برحسب متغیر x است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















