جواب تمرین صفحه 62 درس 2 حسابان یازدهم (تابع)
تعداد بازدید : 80.73Mپاسخ تمرین صفحه 62 حسابان یازدهم
-گام به گام تمرین صفحه 62 درس تابع
-تمرین صفحه 62 درس 2
-شما در حال مشاهده جواب تمرین صفحه 62 حسابان یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 تابعی از دنیای واقعی مثال بزنید که یک به یک نباشد.
ارتباط میان معلم ریاضی و تمام شاگردان یک کلاس
2 آیا تابع \(f\left( x \right) = \frac{2}{5}\) وارون تابع \(g\left( x \right) = \frac{5}{2}\) است؟
خیر؛ زیرا \(\left( {0\;,\;\frac{2}{5}} \right) \in f\) ولی \(\left( {\frac{2}{5}\;,\;0} \right) \notin g\) توابع f و g به خاطر یک به یک نبودن وارون پذیر نیستند.
3 به کمک رسم نمودار وارون پذیری توابع زیر را بررسی کنید و ضابطه تابع وارون را برای هر کدام که وارون پذیرند، به دست آورید:
الف \(f\left( x \right) = {\left( {x + 5} \right)^2}\;\;\;,\;\;\;\;x \ge - 5\)
ب \(f\left( x \right) = - \left| {x - 1} \right| + 1\;\;\;,\;\;\;\;x \ge 2\)
پ \(f\left( x \right) = {(x - 3)^2}\)
ت \(f\left( x \right) = \sqrt {x + 2} - 3\)
الف
\(\begin{array}{l}y = {\left( {x + 5} \right)^2} \Rightarrow \pm \sqrt y = x + 5\\\;\mathop \Rightarrow \limits^{\left( i \right)} \;\sqrt y = x + 5\\ \Rightarrow x = \sqrt y - 5 \Rightarrow {f^{ - 1}}\left( y \right) = \sqrt y - 5\\ \Rightarrow {f^{ - 1}}\left( x \right) = \sqrt x - 5\\\left\{ \begin{array}{l}{D_{{f^{ - 1}}}} = \left[ {0\;,\;\infty } \right)\\{R_{{f^{ - 1}}}} = \left[ { - 5\;,\;\infty } \right)\end{array} \right.\end{array}\)
تابع f وارون پذیر است
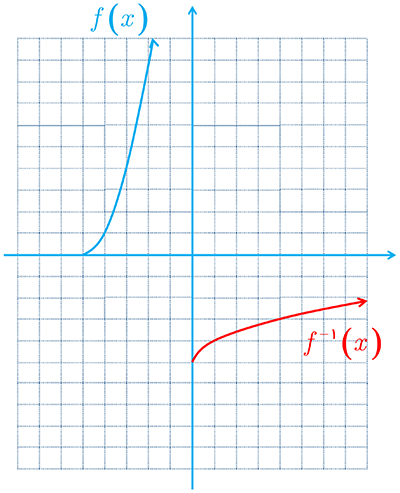
ب
\(\begin{array}{l}\left\{ \begin{array}{l}{D_f} = \left[ {2\;,\;\infty } \right)\\{R_f} = \left( { - \infty \;,\;0} \right]\quad \left( i \right)\end{array} \right.\\y = - \left| {x - 1} \right| + 1 \Rightarrow y - 1 = - \left| {x - 1} \right| \\\Rightarrow \;1 - y\; = \left| {x - 1} \right|\\ \Rightarrow \pm \left( {\;1 - y} \right) = x - 1\\\;\mathop \Rightarrow \limits^{\left( i \right)} \;\left( {\;1 - y} \right) = x - 1 \Rightarrow x = 2 - y\\{f^{ - 1}}\left( y \right) = 2 - y \Rightarrow {f^{ - 1}}\left( x \right) = 2 - x\\\left\{ \begin{array}{l}{D_{{f^{ - 1}}}} = \left( { - \infty \;,\;0} \right]\\{R_{{f^{ - 1}}}} = \left[ {2\;,\;\infty } \right)\end{array} \right.\end{array}\)
تابع f وارون پذیر است
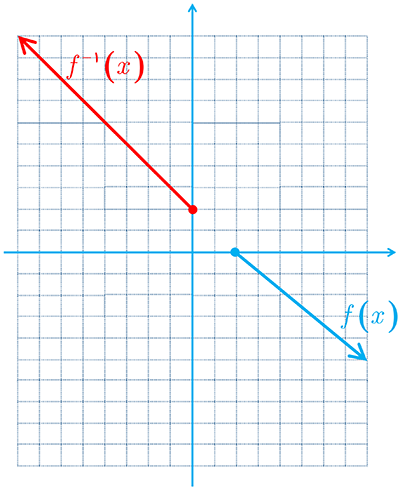
پ
تابع f وارون پذیر نیست
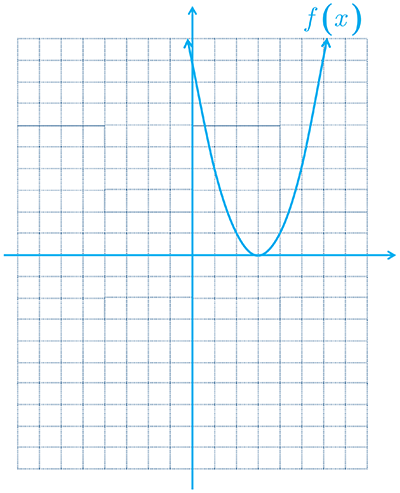
ت
\(\begin{array}{l}\left\{ \begin{array}{l}{D_f} = \left[ { - 2\;,\;\infty } \right)\\{R_f} = \left[ { - 3\;,\;\infty } \right)\quad \left( i \right)\end{array} \right.\\\\y = \sqrt {x + 2} - 3 \Rightarrow y + 3 = \sqrt {x + 2} \\\\\Rightarrow {\left( {y + 3} \right)^2} = x + 2\\\\ \Rightarrow x = {\left( {y + 3} \right)^2} - 2\\\\\left\{ \begin{array}{l}{D_{{f^{ - 1}}}} = \left[ { - 3\;,\;\infty } \right)\\{R_{{f^{ - 1}}}} = \left[ { - 2\;,\;\infty } \right)\end{array} \right.\end{array}\)
تابع f وارون پذیر است
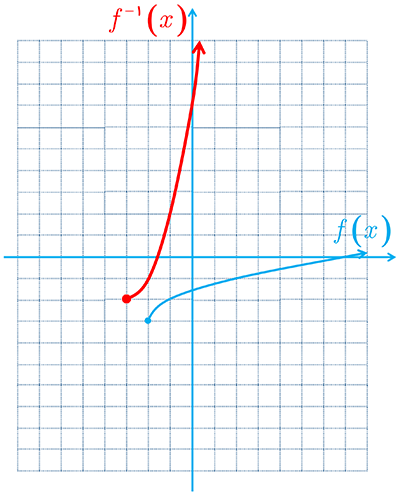
4 اگر سنگی از ارتفاع 100 متری سقوط کند، ارتفاع آن (h برحسب متر) بعد از t ثانیه از رابطهٔ \(h\left( t \right) = 100 - 5{t^2}\) به دست می آید.
الف دامنه و برد h را به دست آورید.
ب چرا h تابعی یک به یک است؟
پ تابع وارون h را به دست آورید.
الف
\(\begin{array}{l}h\left( t \right) = 100 - 5{t^2} \Rightarrow 0 = 100 - 5{t^2}\\\\ \Rightarrow {t^2} = 20 \Rightarrow \left\{ \begin{array}{l}t = \pm \sqrt {20} \\t \ge 0\end{array} \right. \\\\\Rightarrow t = \sqrt {20} \\\\\left\{ \begin{array}{l}{D_h} = \left[ {0\;,\;\sqrt {20} } \right]\\{R_h} = \left[ {0\;,\;100} \right]\end{array} \right.\end{array}\)
ب زیرا به هر ارتفاعی از برد، تنها و تنها یک زمان از دامنه نظیر می شود.
پ
\(\begin{array}{l}\left\{ \begin{array}{l}{D_h} = \left[ {0\;,\;\sqrt {20} } \right]\\{R_h} = \left[ {0\;,\;100} \right]\end{array} \right.\\\\h\left( t \right) = y = 100 - 5{t^2} \Rightarrow {t^2} = \frac{{100 - y}}{5} \\\\\Rightarrow t = \sqrt {\frac{{100 - y}}{5}} \\\\ \Rightarrow {h^{ - 1}}\left( t \right) = \sqrt {\frac{{100 - t}}{5}} \\\\\left\{ \begin{array}{l}{D_{{h^{ - 1}}}} = \left[ {0\;,\;100} \right]\\{R_{{h^{ - 1}}}} = \left[ {0\;,\;\sqrt {20} } \right]\end{array} \right.\end{array}\)
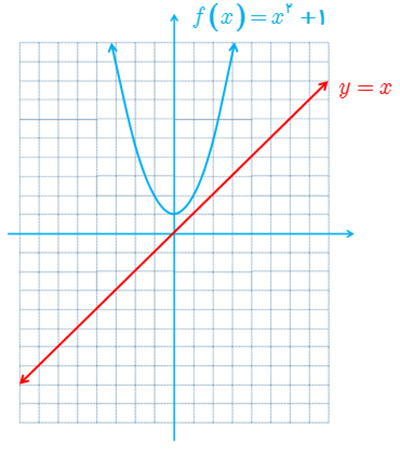
5 نمودار تابعی مانند f را رسم کنید که وارون پذیر نباشد و برای هر عدد حقیقی x داشته باشیم x<f(x).
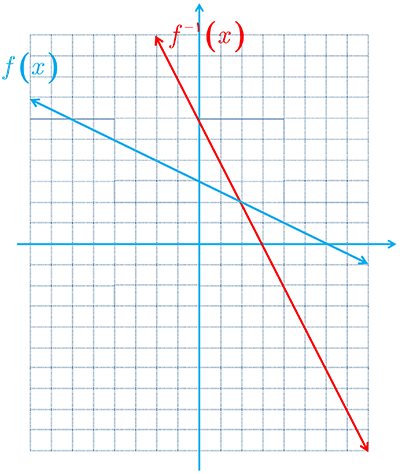
6 وارون تابع \(f\left( x \right) = - \frac{1}{2}x + 3\) را بیابید و نمودار f و وارون آن را رسم کنید.
\(\begin{array}{l}f\left( x \right) = - \frac{1}{2}x + 3\\\\y = - \frac{1}{2}x + 3 \Rightarrow y - 3 = - \frac{1}{2}x \\\\\Rightarrow x = - 2\left( {y - 3} \right)\\\\ \Rightarrow {f^{ - 1}}\left( y \right) = - 2y + 6 \\\\\Rightarrow {f^{ - 1}}\left( x \right) = - 2x + 6\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















