1736019749.png)
جواب فعالیت صفحه 106 درس 4 حسابان یازدهم (مثلثات)
تعداد بازدید : 78.86Mپاسخ فعالیت صفحه 106 حسابان یازدهم
-گام به گام فعالیت صفحه 106 درس مثلثات
-فعالیت صفحه 106 درس 4
-شما در حال مشاهده جواب فعالیت صفحه 106 حسابان یازدهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
1 همانند فعالیت قبل، تابع y=cosx در زیر رسم شده است. مجموعه زوج های مرتب داده شده از این تابع را تکمیل کنید و نقاط به دست آمده را مانند نمونه بر روی نمودار نمایش دهید.
\(\begin{array}{l}f = \{ \left( {0,1} \right)\;,\;\left( {\frac{\pi }{3},\frac{1}{2}} \right)\;,\;\left( {\frac{\pi }{2},...} \right)\;,\;\left( {\frac{{2\pi }}{3},...} \right)\;,\;\\\\\left( {\pi , - 1} \right)\;,\;\left( {\frac{{4\pi }}{3},...} \right)\;,\;\left( {\frac{{3\pi }}{2},...} \right)\;,\;\\\\\left( {\frac{{5\pi }}{3},...} \right)\;,\;\left( {2\pi ,...} \right)\} \end{array}\)
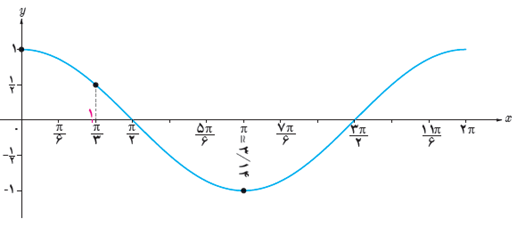
\(\begin{array}{l}f = \{ \left( {0,1} \right)\;,\;\left( {\frac{\pi }{3},\frac{1}{2}} \right)\;,\;\left( {\frac{\pi }{2},0} \right)\;,\;\left( {\frac{{2\pi }}{3}, - \frac{1}{2}} \right)\;,\;\\\\\left( {\pi , - 1} \right)\;,\;\left( {\frac{{4\pi }}{3}, - \,\frac{1}{2}} \right)\;,\;\left( {\frac{{3\pi }}{2},0} \right)\;,\;\\\\\left( {\frac{{5\pi }}{3},\frac{1}{2}} \right)\;,\;\left( {2\pi ,1} \right)\} \end{array}\)
2 در نمودار بالا ابتدا نقطه نظیر \(\sqrt 2 \) رادیان را بر روی محور xها بیابید و سپس مکان \(\cos \sqrt 2 \) را بر روی محور yها به طور تقریبی پیدا کنید. درستی پاسخ خود را با ماشین حساب بررسی کنید.
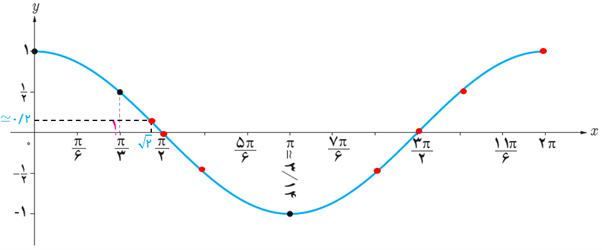
\(\cos {\left( {\sqrt 2 } \right)^{rad}} \simeq 0/15\)
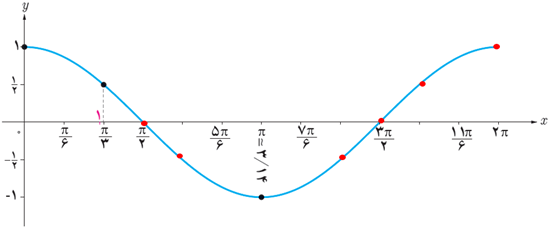
3 از درس های قبل می دانیم که cos(x+2kπ)=cosx و نیز cos(-x)=cosx با استفاده از این روابط مقدار تابع y=cosx را در دیگر نقاط داده شده بر روی محور xها به دست آورید و نمودار تابع را از دو طرف ادامه دهید. آیا نمودار این تابع در بازه های \([2π , 4π]\)و \([0 , 2π]\)و \([-2π , 0]\) با هم متفاوت هستند؟
خیر؛ بلکه همه با هم یکسان هستند :
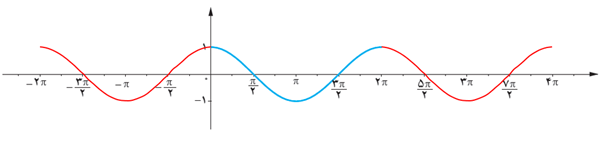
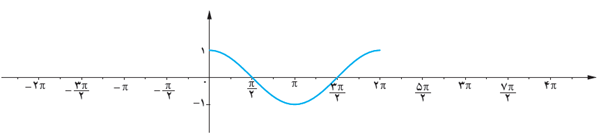
4 باتوجه به نمودار تابع y=cosx در بازه \([-2π , 4π]\) به سؤالات زیر پاسخ دهید.
الف آیا می توان بر روی محور xها عددی مانند x یافت که برای آن \(\cos x = \frac{1}{3}\) باشد؟
ب آیا می توان بر روی محور xها عددی مانند x یافت که برای آن cosx=2 باشد؟
پ بیشترین و کمترین مقدار تابع y=cosx در این بازه چقدر است؟
الف
بله؛ 6 عدد بر روی محور طول ها وجود دارد که : \(\cos {x_ \circ } = \frac{1}{3}\)
ب
خیر؛ چنین عددی بر محور طول ها وجود ندارد.
پ
\(\left\{ \begin{array}{l}{y_{Max}} = 1\\{y_{Min}} = - 1\end{array} \right. \Rightarrow - 1 \le \cos x \le 1\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
