گام به گام مثال صفحه 19 درس ترسیم های هندسی و استدلال هندسه (1)
تعداد بازدید : 50.06Mپاسخ مثال صفحه 19 هندسه (1)
-گام به گام مثال صفحه 19 درس ترسیم های هندسی و استدلال
-مثال صفحه 19 درس 1
-مثال: استدلال استنتاجی زیر را کامل کنید و نتیجه بگیرید که سه ارتفاع هر مثلث همرس اند.
استدلال: مثلث دلخواه ABC را در نظر بگیرید و از هر رأس آن خطی به موازات ضلع مقابل به آن رأس رسم کنید تا مطابق شکل مقابل مثلثی مانند DEF به وجود آید.
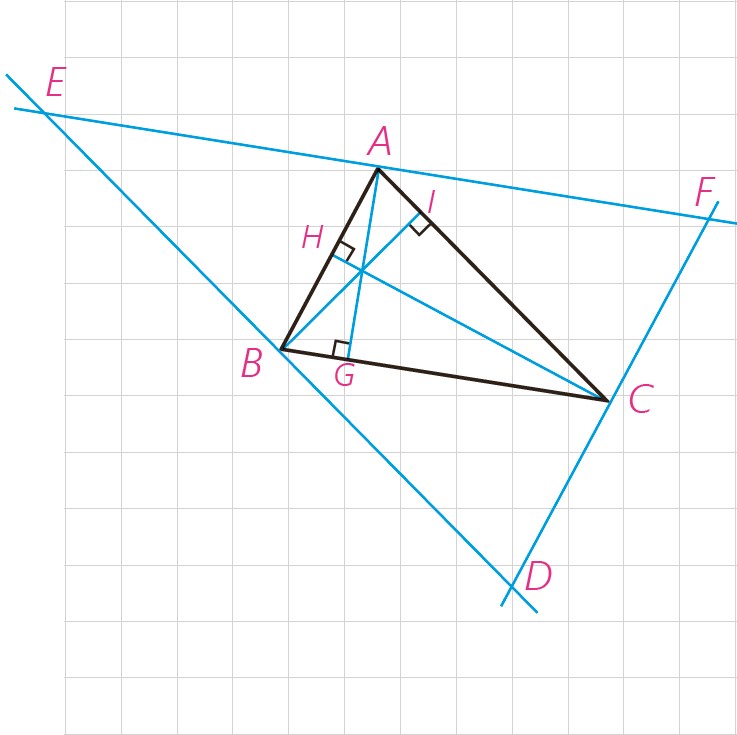
مثلث ABC با مثلث های ACF و ABE همنهشت است (چرا؟).
چهار ضلعی ABCF متوازی الاضلاع است، زیرا ضلع های AB و CF و ضلع های BC و AF دو به دو با هم موازی اند. در نتیجه داریم:
\(\left\{ \begin{array}{l}AB = CF\\\\BC = AF\\\\AC = AC\end{array} \right. \Rightarrow A\mathop B\limits^\Delta C \cong A\mathop C\limits^\Delta F\)
همچنین چهار ضلعی AEBC متوازی الاضلاع است، زیرا ضلع های AE و BC و ضلع های AC و EB دو به دو با هم موازی اند در نتیجه داریم:
\(\left\{ \begin{array}{l}AE = BC\\\\EB = AC\\\\AB = AB\end{array} \right. \Rightarrow A\mathop B\limits^\Delta C \cong A\mathop B\limits^\Delta E\)
بنابراین AE=BC=AF و لذا نقطهٔ A .............. پاره خط EF است.
وسط
از طرفی:
\(\left. \begin{array}{l}AG \bot BC\\\\BC\parallel EF\end{array} \right\} \Rightarrow AG\,\,\, \ldots \,\,\,EF\)
\(\left. \begin{array}{l}AG \bot BC\\\\BC\parallel EF\end{array} \right\} \Rightarrow AG\,\,\, \bot \,\,\,EF\)
لذا خط AG .......................................... پاره خط EF است.
عمود منصف
به طور مشابه می توان نشان داد:
پاره خط BI، .......................................... پاره خط DE است.
عمود منصف
پاره خط CH، .......................................... پاره خط DF است.
عمود منصف
بنابراین، ارتفاع های مثلث ABC، روی عمود منصف های اضلاع مثلث ............ هستند و درنتیجه همرس اند.
DEF
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
