گام به گام مثال صفحه 24 درس ترسیم های هندسی و استدلال هندسه (1)
تعداد بازدید : 50.07Mپاسخ مثال صفحه 24 هندسه (1)
-گام به گام مثال صفحه 24 درس ترسیم های هندسی و استدلال
-مثال صفحه 24 درس 1
-مثال: از یک نقطه غیر واقع بر خط نمی توان بیش از یک عمود بر آن خط رسم کرد.
فرض: نقطه ای مانند A غیر واقع بر خطی مانند d وجود دارد.
حکم: از نقطهٔ A نمی توان بیش از یک عمود بر خط d رسم کرد.
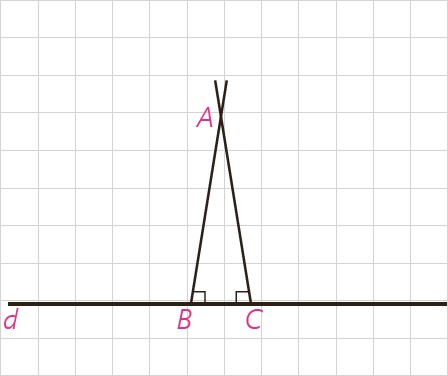
استدلال: با برهان غیرمستقیم فرض می کنیم حکم غلط باشد؛ یعنی فرض می کنیم از نقطهٔ A دو عمود بر خط d رسم کرده ایم که مانند شکل، خط d را در نقاط B و C قطع کرده اند. در این صورت مجموع زوایای داخلی مثلث ABC بزرگ تر از \({180^ \circ }\)
خواهد شد و این غیرممکن است. پس امکان رسم دو عمود از یک نقطهٔ غیر واقع بر یک خطوجود ندارد؛ یعنی حکم نمی تواند غلط باشد.
حال می خواهیم درستی عکس قضیهٔ 1 را با برهان غیرمستقیم ثابت کنیم.
عکس قضیۀ 1: اگر در مثلثی دو زاویه نابرابر باشند، ضلع مقابل به زاویهٔ بزرگ تر، بزرگ تر است از ضلع روبه رو به زاویهٔ کوچک تر.
برای واضح شدن مسئله و کمک به حل آن، شکل مثلث را رسم م یکنیم و با استفاده از آن فرض و حکم را می نویسیم.
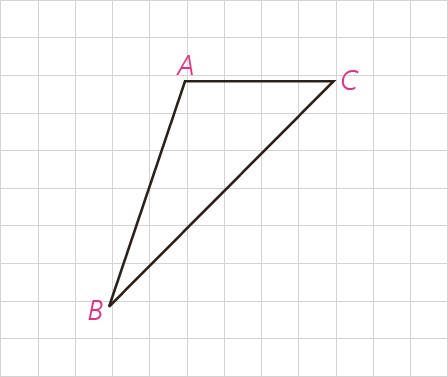
\(\hat A > \hat B\) : فرض
\(BC > AC\) : حکم
اثبات: با برهان غیرمستقیم فرض می کنیم حکم ............... باشد. بنابراین باید ..................... یا ...................... .
نادرست – BC<AC – BC=AC
هر دو حالت را جداگانه بررسی می کنیم و نشان می دهیم هر دو حالت به تناقض منجر می شود.
حالت اول: اگر BC<AC باشد، طبق قضیهٔ ١ باید ...................... که با فرض در تناقض است.
\(\hat A < \hat B\)
حالت دوم: اگر BC=AC باشد، \(A\mathop B\limits^\Delta C\) یک مثلث ................... خواهد بود و می دانیم در این حالت باید \(\hat A = \hat B\) باشد که در تناقض با فرض است. لذا هر دو حالت BC<AC و BC=AC غیرممکن اند؛ بنابراین BC>AC است و حکم درست است.
متساوی الساقین
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
کاملا رایگان
+500 هزار کاربر
همین حالا نصب کن
