جواب مرور فصل 8 صفحه 110 درس 8 ریاضی هفتم (بردار و مختصات)
تعداد بازدید : 86.39Mپاسخ مرور فصل 8 صفحه 110 ریاضی هفتم
-گام به گام مرور فصل 8 صفحه 110 درس بردار و مختصات
-مرور فصل 8 صفحه 110 درس 8
-شما در حال مشاهده جواب مرور فصل 8 صفحه 110 ریاضی هفتم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
مفاهیم و مهارت ها
در این فصل، اصطلاحات زیر به کار رفته اند. مطمئن شوید که می توانید با جملات خود آنها را تعریف کنید و برای هر کدام یک مثال بزنید.
1 بردار
2 راستا
3 بردار انتقال
4 پاره خط جهت دار
۱ بردار:
بردار مثل یه پیکان (فلش) میمونه. این پیکان چندتا چیز مهم رو به ما نشون میده:
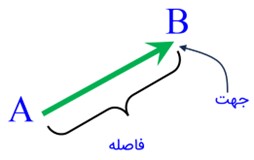
جهت:
نوک پیکان به ما میگه که باید به کدوم سمت بریم (مثلاً راست، چپ، بالا، پایین یا حتی یه جهت کج).
اندازه (طول):
بلندی یا کوتاهی پیکان به ما میگه که چقدر باید در اون جهت حرکت کنیم.
مثال
فرض کن از نقطه A میخوای بری به نقطه B. اگه یه پیکان از A به سمت B بکشی، این یه بردار حساب میشه. جهت پیکان از A به B هست و طول پیکان هم فاصلهی بین A و B رو نشون میده. یا مثلاً وقتی میگی «۳ قدم به سمت شرق»، این خودش یه جورایی داره یه بردار رو توصیف میکنه.

۲ راستا:
راستا یعنی امتداد یا خطی که بردار روش قرار گرفته یا باهاش موازیه. فکر کن یه جادهی صاف و طولانی داری. اون جاده میتونه راستای حرکت یه ماشین باشه.
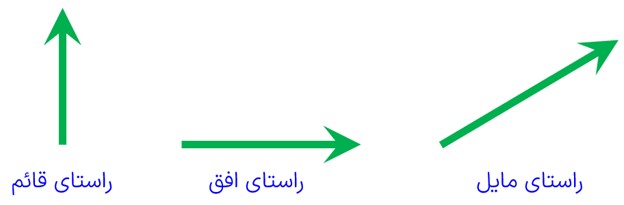
بردارها میتونن راستای افقی (مثل خط افق)، عمودی (مثل یه تیر چراغ برق صاف) یا مایل (کج) داشته باشن.
مثال
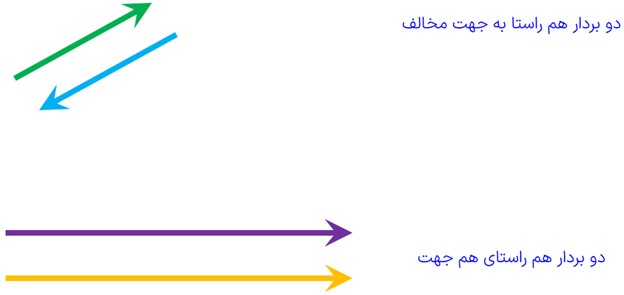
اگه یه بردار از سمت چپ دفترت به سمت راست دفترت کشیده باشی، راستای این بردار افقی هست. اگه دو تا بردار داشته باشیم که هر دو روی خطهای موازی باشن، میگیم همراستا هستن، حتی اگه جهتشون مخالف هم باشه (یکی به راست، یکی به چپ).
۳ بردار انتقال:
بردار انتقال یه نوع خاص از برداره که به ما میگه یه شکل یا یه نقطه رو چطوری از یه جا به یه جای دیگه منتقل کنیم یا جابجا کنیم، بدون اینکه شکلش یا اندازهاش تغییر کنه یا بچرخه. فقط جابجا میشه!
مثال
فرض کن یه مربع روی صفحهی مختصات داری. اگه بخوای این مربع رو ۲ واحد به سمت راست و ۳ واحد به سمت بالا ببری، از یه بردار انتقال استفاده میکنی. این بردار به همهی گوشههای مربع میگه که دقیقاً چقدر و به کدوم سمت حرکت کنن تا مربع به جای جدیدش منتقل بشه. مثلاً برداری که به سمت راست ۲ واحد و به سمت بالا ۳ واحد حرکت رو نشون میده، میشه بردار انتقال ما.
۴ پاره خط جهت دار:
پارهخط جهتدار دقیقاً همون چیزیه که از اسمش پیداست:
پارهخط:
یه تیکه از یه خط راسته که دو تا نقطه ابتدا و انتها داره.
جهتدار:
یکی از اون دو تا نقطه، نقطه شروع حساب میشه و اون یکی نقطه پایان. پس یه جهت مشخص از شروع به پایان داره.
در واقع، هر بردار رو میتونیم با یه پارهخط جهتدار نشون بدیم. نقطهی شروع پارهخط، ابتدای بردار و نقطهی پایان پارهخط، انتهای بردار (نوک پیکان) هست.
مثال
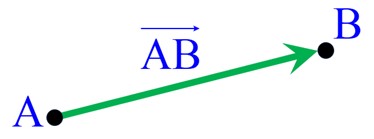
اگه روی کاغذ دو نقطه A و B داشته باشی و یه خط راست از A به B بکشی و یه فلش کوچیک روی B (به سمت خارج از A) بذاری، این یه پارهخط جهتدار از A به B هست. این پارهخط جهتدار، بردار AB رو نشون میده.
در این فصل، روش های اصلی زیر مطرح شده اند. با یک مثال هر کدام را توضیح دهید و در دفتر خود یک خلاصهٔ درس تهیه کنید.
1 ویژگی ها، نام گذاری و نمایش بردار
2 مختصات نقطه در صفحه
3 بردار انتقال
4 جمع متناظر با بردار
5 پیدا کردن مختصات بردار
6 بردار قرینه و بردار صفر
7 4 ناحیۀ محور مختصات
8 بردارهای مساوی
1 ویژگی ها، نام گذاری و نمایش بردار
ویژگیها:
هر بردار سه تا چیز مهم داره:
اندازه (طول):
میگه چقدر بلند یا کوتاهه.
راستا:
خطی که بردار روش قرار داره (افقی، عمودی، یا کج).
جهت (سو):
نوک پیکان نشون میده به کدوم سمت میره.
نامگذاری:
بردارها رو معمولاً با دو حرف بزرگ که ابتدا و انتهاش رو نشون میدن و یه فلش کوچیک بالاشون مینویسن (مثل \(\overrightarrow {AB} \) یعنی برداری که از نقطه A شروع میشه و به نقطه B میره) یا با یه حرف کوچیک انگلیسی و یه فلش بالاش (مثل \(\overrightarrow a \)).
نمایش:
بردار رو با یه پیکان (فلش) روی کاغذ یا صفحه مختصات نشون می دیم.
مثال
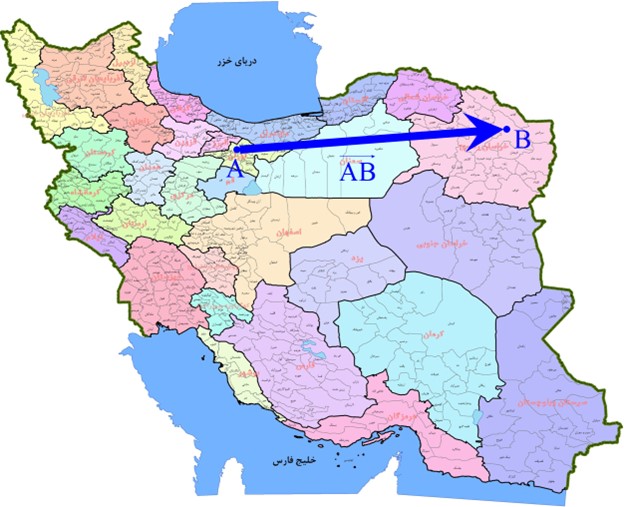
فرض کنید یک هواپیما از تهران (نقطه A) به سمت مشهد (نقطه B) با سرعت و در مسیری مشخص پرواز میکند. این جابجایی را میتوان با بردار \(\overrightarrow {AB} \) نمایش داد.
اندازه بردار: فاصله هوایی مستقیم بین تهران و مشهد.
جهت بردار: از سمت تهران به سمت مشهد.
2 مختصات نقطه در صفحه:
برای تعیین دقیق موقعیت یک نقطه در یک صفحه، از دستگاه مختصات دکارتی استفاده میشود. این دستگاه از دو محور عمود بر هم تشکیل شده است: محور طولها (محور x) که افقی است و محور عرضها (محور y) که عمودی است. محل برخورد این دو محور، مبدأ مختصات نام دارد و با (0 , 0) نمایش داده میشود.
موقعیت هر نقطه با یک زوج مرتب به صورت (x , y) مشخص میشود. عدد اول (x) فاصله افقی نقطه از محور عرضها، و عدد دوم (y) فاصله عمودی نقطه از محور طولها را نشان میدهد.
مثال
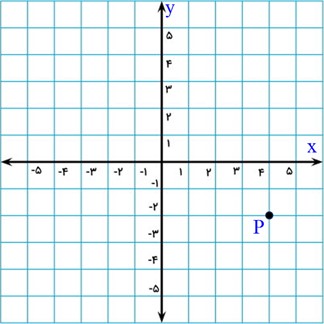
نقطۀ P با مختصات \(\left[ {\begin{array}{*{20}{c}}4\\{ - 2}\end{array}} \right]\) را در نظر بگیرید:
عدد 4 (مؤلفۀ x) نشان می دهد که نقطۀ P به اندازه 4 واحد در جهت مثبت محور x (به سمت راستِ مبدأ) قرار دارد.
عدد -2 (مؤلفۀ y) نشان می دهد که نقطۀ P به اندازه 2 واحد در جهت منفی محور y (به سمت پایین مبدأ) قرار دارد.
3 بردار انتقال:
بردار انتقال برداری است که جابجایی یک نقطه یا یک شکل را از یک مکان اولیه به یک مکان ثانویه توصیف میکند. این بردار، هم جهت و هم میزان این جابجایی را به طور دقیق مشخص میکند.
مثال
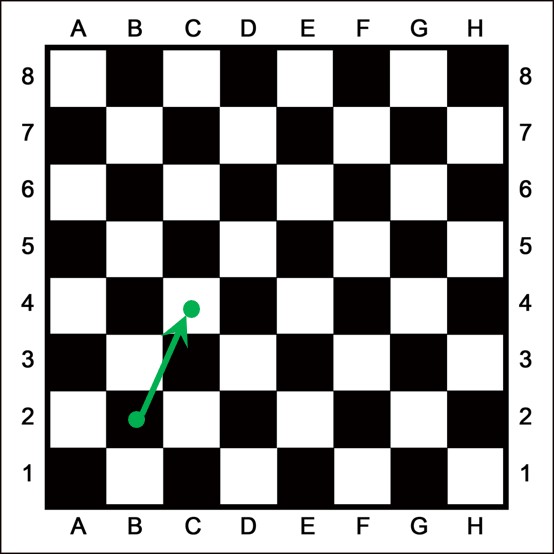
فرض کنید یک مهره شطرنج از خانهB-2 با مختصات \(\left[ {\begin{array}{*{20}{c}}2\\2\end{array}} \right]\) به خانه C-4 با مختصات \(\left[ {\begin{array}{*{20}{c}}3\\4\end{array}} \right]\) روی صفحه شطرنج منتقل میشود. بردار انتقال زیر، این حرکت را نشان می دهد. این بردار بیان می کند که مهره 1 واحد در راستای افق (3-2=1) و 2 واحد در راستای عمودی (4-2=2) جابجا شده است.
4 جمع متناظر با بردار:
منظور از «جمع متناظر با بردار»، همان عملیات جمع برداری است. وقتی دو یا چند بردار را با هم جمع میکنیم، در واقع اثر ترکیبی آنها را محاسبه میکنیم. یکی از روشهای رایج برای جمع دو بردار، روش مثلث است:
انتهای بردار اول را به ابتدای بردار دوم متصل میکنیم. برداری که از ابتدای بردار اول به انتهای بردار دوم رسم میشود، بردار حاصل جمع (یا بردار برآیند) نام دارد.
مثال
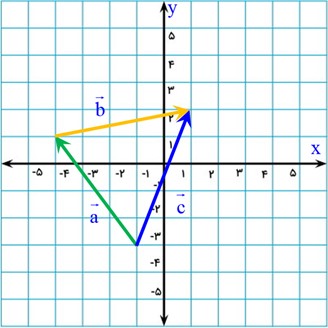
شخصی ابتدا با بردار \(\overrightarrow a = \left[ {\begin{array}{*{20}{c}}{ - 3}\\4\end{array}} \right]\) مسافتی را طی میکند (مثلاً ۴ کیلومتر به شرق) و سپس از همان نقطه، با بردار \(\overrightarrow b = \left[ {\begin{array}{*{20}{c}}5\\1\end{array}} \right]\) مسافت دیگری را طی میکند (مثلاً ۳ کیلومتر به شمال). بردار \(\overrightarrow c = \overrightarrow a + \overrightarrow b \) جابجایی کل این شخص را از نقطه شروع اولیه تا نقطه پایان ثانویه نشان میدهد.
\(\overrightarrow c = \overrightarrow a + \overrightarrow b = \left[ {\begin{array}{*{20}{c}}{ - 3}\\4\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}5\\1\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{ - 3 + 5}\\{4 + 1}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}2\\5\end{array}} \right]\)
5 پیدا کردن مختصات بردار:
اگر مختصات نقطه ابتدای یک بردار، \(A = \left[ {\begin{array}{*{20}{c}}{{x_1}}\\{{y_1}}\end{array}} \right]\)، و مختصات نقطه انتهای آن، \(B = \left[ {\begin{array}{*{20}{c}}{{x_2}}\\{{y_2}}\end{array}} \right]\)، معلوم باشد، مختصات بردار AB به صورت زیر محاسبه میشود:
\(\overrightarrow {AB} = \left[ {\begin{array}{*{20}{c}}{{x_2} - {x_1}}\\{{y_2} - {y_1}}\end{array}} \right]\)
مقدار اول \(({x_2} - {x_1})\)، میزان جابجایی افقی (مولفه x بردار) و مقدار دوم \(({y_2} - {y_1})\)، میزان جابجایی عمودی (مولفه y بردار) را نشان میدهد.
مثال
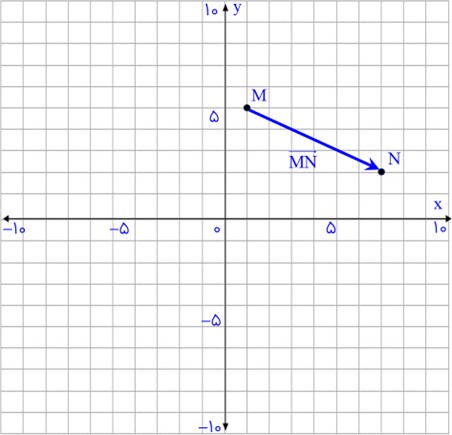
اگر نقطه شروع یک بردار \(M = \left[ {\begin{array}{*{20}{c}}1\\5\end{array}} \right]\) و نقطه پایان آن \(N = \left[ {\begin{array}{*{20}{c}}7\\2\end{array}} \right]\) باشد، مختصات بردار MN عبارت است از:
\(\overrightarrow {MN} = \left[ {\begin{array}{*{20}{c}}7\\2\end{array}} \right] - \left[ {\begin{array}{*{20}{c}}1\\5\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{7 - 1}\\{2 - 5}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}6\\{ - 3}\end{array}} \right]\)
6) بردار قرینه و بردار صفر
بردار قرینه:
بردار قرینه یک بردار v، برداری است که هماندازه باv میباشد اما جهتی دقیقاً مخالف جهت v دارد. اگر مختصات بردار \(\overrightarrow v = \left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right]\) باشد، مختصات بردار قرینه آن، \(\overrightarrow {v'} = - \overrightarrow v = \left[ {\begin{array}{*{20}{c}}{ - x}\\{ - y}\end{array}} \right]\) خواهد بود. حاصل جمع هر بردار با قرینهاش، بردار صفر است:
\(\overrightarrow v + \overrightarrow {v'} = \left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}{ - x}\\{ - y}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{x + ( - x)}\\{y + ( - y)}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}0\\0\end{array}} \right]\)
بردار صفر:
برداری است که اندازه آن صفر است و جهت معینی ندارد. مختصات بردار صفر \(\left[ {\begin{array}{*{20}{c}}0\\0\end{array}} \right]\) است. این بردار نشاندهنده عدم جابجایی است؛ یعنی نقطه ابتدا و انتهای آن بر هم منطبق هستند.
مثال
اگر بردار \(\overrightarrow d = \left[ {\begin{array}{*{20}{c}}{ - 2}\\5\end{array}} \right]\) باشد، بردار قرینۀ آن \(\overrightarrow {d'} = \left[ {\begin{array}{*{20}{c}}2\\{ - 5}\end{array}} \right]\) می باشد:
\(\overrightarrow d + \overrightarrow {d'} = \left[ {\begin{array}{*{20}{c}}2\\{ - 5}\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}{ - 2}\\5\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{2 + ( - 2)}\\{ - 5 + 5}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}0\\0\end{array}} \right]\)
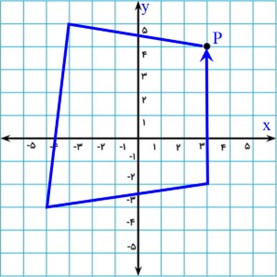
اگر یک جسم از نقطه \(P = \left[ {\begin{array}{*{20}{c}}3\\4\end{array}} \right]\) شروع به حرکت کند و پس از طی مسیری دوباره به همان نقطه \(P = \left[ {\begin{array}{*{20}{c}}3\\4\end{array}} \right]\) بازگردد، بردار جابجایی کلی آن، بردار صفر خواهد بود:
\(\overrightarrow {PP} = \left[ {\begin{array}{*{20}{c}}3\\4\end{array}} \right] - \left[ {\begin{array}{*{20}{c}}3\\4\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{3 - 3}\\{4 - 4}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}0\\0\end{array}} \right]\)
7) 4 ناحیۀ محور مختصات
محورهای مختصات، صفحه را به چهار بخش مجزا تقسیم میکنند که هر یک از این بخشها یک ناحیه یا رُبع نامیده میشود. این ناحیهها به صورت قراردادی و در خلاف جهت حرکت عقربههای ساعت شمارهگذاری میشوند:
ناحیه اول: شامل نقاطی است که هم طول (x) و هم عرض (y) آنها مثبت است (x>0 , y>0).
ناحیه دوم: شامل نقاطی است که طول (x) آنها منفی و عرض (y) آنها مثبت است (x<0 , y>0).
ناحیه سوم: شامل نقاطی است که هم طول (x) و هم عرض (y) آنها منفی است (x<0 , y<0).
ناحیه چهارم: شامل نقاطی است که طول (x) آنها مثبت و عرض (y) آنها منفی است (x>0 , y<0). نقاطی که روی یکی از محورها قرار دارند، متعلق به هیچیک از این چهار ناحیه نیستند.
مثال
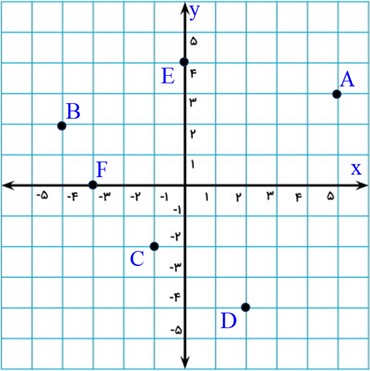
نقطه \(A = \left[ {\begin{array}{*{20}{c}}5\\3\end{array}} \right]\) در ناحیه اول قرار دارد.
نقطه \(B = \left[ {\begin{array}{*{20}{c}}{ - 4}\\2\end{array}} \right]\) در ناحیه دوم قرار دارد.
نقطه \(C = \left[ {\begin{array}{*{20}{c}}{ - 1}\\{ - 2}\end{array}} \right]\) در ناحیه سوم قرار دارد.
نقطه \(A = \left[ {\begin{array}{*{20}{c}}2\\{ - 4}\end{array}} \right]\) در ناحیه چهارم قرار دارد.
نقطه \(E = \left[ {\begin{array}{*{20}{c}}0\\4\end{array}} \right]\) روی محور عرض ها (محور y) و نقطه \(F = \left[ {\begin{array}{*{20}{c}}{ - 3}\\0\end{array}} \right]\) روی محور طول ها (محور x) قرار دارد.
8 بردارهای مساوی:
دو بردار زمانی مساوی هستند که هم اندازه (طول) یکسانی داشته باشند و هم جهت آنها کاملاً یکسان باشد. محل قرارگیری یا نقطه شروع بردارها در تساوی آنها تأثیری ندارد.
مثال
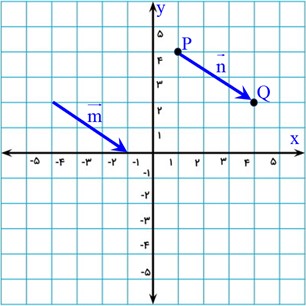
فرض کنید بردار \(\overrightarrow m = \left[ {\begin{array}{*{20}{c}}3\\{ - 2}\end{array}} \right]\) است. بردار دیگری، n، از نقطه \(P = \left[ {\begin{array}{*{20}{c}}1\\4\end{array}} \right]\) به نقطه \(Q = \left[ {\begin{array}{*{20}{c}}4\\2\end{array}} \right]\) رسم شده است. مختصات بردار n عبارت است از:
\(\overrightarrow n = \overrightarrow {PQ} = \left[ {\begin{array}{*{20}{c}}4\\2\end{array}} \right] - \left[ {\begin{array}{*{20}{c}}1\\4\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}3\\{ - 2}\end{array}} \right]\)
از آن جایی که مختصات بردارهای m و n هر دو \(\left[ {\begin{array}{*{20}{c}}3\\{ - 2}\end{array}} \right]\) است، بنابراین \(\overrightarrow m = \overrightarrow n \) . این دو بردار، با وجود داشتن نقاط شروع متفاوت، نشاندهنده یک جابجایی یکسان (۳ واحد به راست و ۲ واحد به پایین) هستند.
تمرین های ترکیبی
در صورتی که بتوانید تمرین های ترکیبی زیر را انجام دهید، مطمئن می شوید که این فصل را به خوبی آموخته اید.
1 الف نقاط به مختصات \(A = \left[ \begin{array}{l}1/5\\\;\;2\end{array} \right]\;\;B = \left[ \begin{array}{l} - 1\\\;2\end{array} \right]\;\;C = \left[ \begin{array}{l}0\\3\end{array} \right]\) را پیدا کنید.
ب نقطه A را با بردار BC منتقل کنید و مختصات نقطه منتقل شده را بنویسید.
پ بدون رسم شکل، ابتدا مختصات بردار BC را پیدا کنید.
ت بدون رسم شکل، انتقال را انجام دهید.
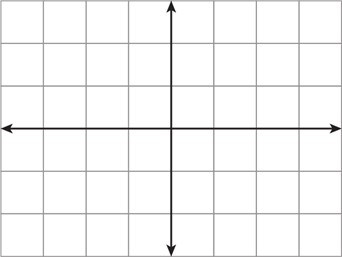
الف
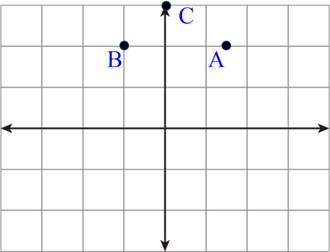
ب
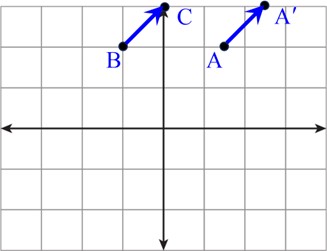
پ
\(\overrightarrow {BC} = \left[ {\begin{array}{*{20}{c}}0\\3\end{array}} \right] - \left[ {\begin{array}{*{20}{c}}{ - 1}\\2\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{0 - ( - 1)}\\{3 - 2}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}1\\1\end{array}} \right]\)
ت
\(A' = A + \overrightarrow {BC} = \left[ {\begin{array}{*{20}{c}}{1/5}\\2\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}1\\1\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{2/5}\\3\end{array}} \right]\)
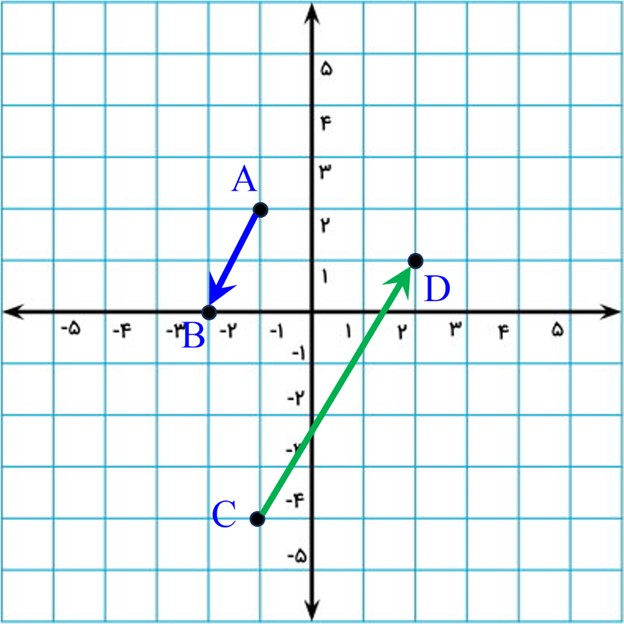
2 بردار خواسته شده را رسم کنید:
الف بردار \(\overrightarrow {AB} = \left[ \begin{array}{l} - 1\\ - 2\end{array} \right]\) ابتدا در \(\left[ \begin{array}{l} - 1\\\;2\end{array} \right]\)
ب بردار \(\overrightarrow {CD} = \left[ \begin{array}{l}3\\5\end{array} \right]\) انتها در \(\left[ \begin{array}{l}2\\1\end{array} \right]\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















