جواب تمرین صفحه 92 درس 7 ریاضی هفتم (توان و جذر)

عددهای بسیاری را می توان قرار داد. برای نمونه عددهای زیر را قرار می دهیم:

\(\begin{array}{l}{a^b} \times {a^c} = {a^{b + c}}\\\\\left\{ \begin{array}{l}a = 4\\\\b = 3\\\\c = 2\end{array} \right. \Rightarrow {4^3} \times {4^2} = {4^{3 + 2}} = {4^5}\\\\\left\{ \begin{array}{l}a = 3\\\\b = 2\\\\c = 2\end{array} \right. \Rightarrow {3^3} \times {3^2} = {3^{3 + 2}} = {3^5}\end{array}\)

\(\begin{array}{l}{a^c} \times {b^c} = {\left( {a \times b} \right)^c}\\\\\left\{ \begin{array}{l}a = 5\\\\b = 4\\\\c = 2\end{array} \right. \Rightarrow {5^2} \times {4^2} = {(5 \times 4)^2} = {20^2}\\\\\left\{ \begin{array}{l}a = 3\\\\b = 5\\\\c = 2\end{array} \right. \Rightarrow {3^2} \times {5^2} = {(3 \times 5)^2} = {15^2}\end{array}\)

\(121 = {11^2}\)

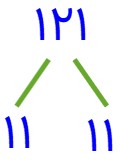
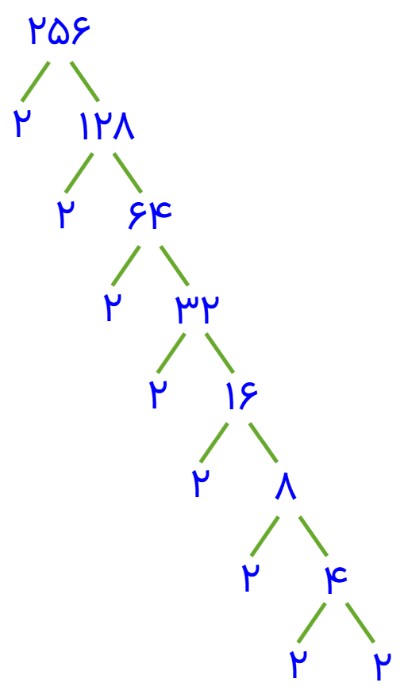
\(\begin{array}{l}256 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 = \\\\{2^8}\end{array}\)

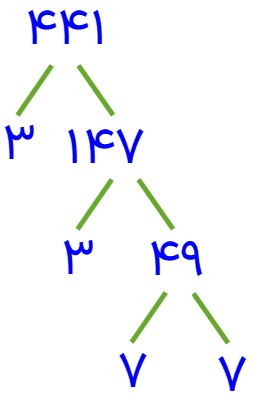
\(\begin{array}{l}441 = 3 \times 3 \times 7 \times 7 = {3^2} \times {7^2} = \\\\{(3 \times 7)^2} = {21^2}\end{array}\)

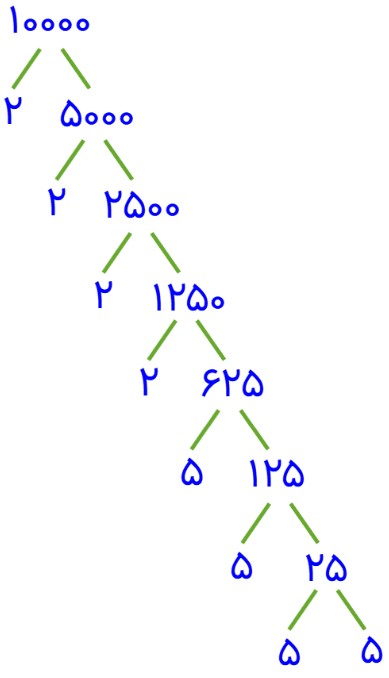
\(\begin{array}{l}10000 = 2 \times 2 \times 2 \times 2 \times 5 \times 5 \times 5 \times 5 = \\\\{2^4} \times {5^4} = {(2 \times 5)^4} = {10^4}\end{array}\)

الف

\({2^3}\) : حجم مکعبی به ضلع 2 سانتی متر را محاسبه کنید.

ب

\(2 \times 3\) : عدد 6 از حاصل ضرب کدام دو عدد اوّل به دست می آید؟

ج

\({5^2}\) مساحت مربعی به ضلع 5 سانتی متر را به صورت یک عدد توان دار نشان دهید.

در مقایسه اعداد توان دار به یکی از سه صورت زیر عمل می کنیم:

1) در صورت امکان، پایه همه اعداد را با هم برابر می کنیم.

2) در صورت امکان، توان همه اعداد را با هم برابر می کنیم.

3) اگر نتوانیم پایه ها و یا توان ها را با هم برابر کنیم، باید مقدار عددها را بدست بیاوریم و سپس آن ها را با هم مقایسه کنیم.

در مورد اعداد داده شده نمی توانیم پایه ها و یا توان ها را با هم برابر کنیم؛ بنابراین مقدار عددها را بدست می آوریم:

\({3^5} = {3^3} \times {3^2} = 27 \times 9 = 243\)

\(\begin{array}{l}{4^{10}} = {4^3} \times {4^3} \times {4^4} = \\\\64 \times 64 \times 256 = 1,048,576\end{array}\)

\({6^0} = 1\)

\({8^1} = 8\)

\({9^2} = 9 \times 9 = 81\)

\(\begin{array}{l} \Rightarrow 1 < 8 < 81 < 243 < 1,048,576\\\\ \Rightarrow {6^0} < {8^1} < {9^2} < {3^5} < {4^{10}}\end{array}\)

\({4^3} \times {4^4} = {4^{12}}\)

نادرست است؛ زیرا:

\({4^3} \times {4^4} = {4^{3 + 4}} = {4^7} \ne {4^{12}}\)

\({3^2} \times {2^3} = {6^5}\)

نادرست است؛ زیرا:

\(\begin{array}{l}\left\{ \begin{array}{l}{3^2} \times {2^3} = 9 \times 8 = 72\\\\{6^5} = {6^2} \times {6^3} = 36 \times 216 = 7776\end{array} \right.\\\\ \Rightarrow {3^2} \times {2^3} \ne {6^5}\end{array}\)

\({4^3} + {2^3} = {6^3}\)

نادرست است؛ زیرا:

\(\begin{array}{l}\left\{ \begin{array}{l}{4^3} + {2^3} = 64 + 8 = 72\\\\{6^3} = 216\end{array} \right.\\\\ \Rightarrow {4^3} + {2^3} \ne {6^3}\end{array}\)

\({4^3} \times {4^4} = {4^7}\)

درست می باشد؛ زیرا:

\({4^3} \times {4^4} = {4^{3 + 4}} = {4^7}\)

\({3^2} \times {2^2} = {6^2}\)

درست می باشد؛ زیرا:

\({3^2} \times {2^2} = {(3 \times 2)^2} = {6^2}\)

\({4^1} + {3^1} = {7^1}\)

درست می باشد؛ زیرا:

\({4^1} + {3^1} = 4 + 3 = 7 = {7^1}\)

\(\left( { - {2^3}} \right) \times {7^3} = {\left( { - 14} \right)^3}\)

درست می باشد؛ زیرا:

\(\begin{array}{l}\left( { - {2^3}} \right) \times {7^3} = \left( { - 8} \right) \times {7^3} = \\\\{\left( { - 2} \right)^3} \times {7^3} = {\left( {( - 2) \times 7} \right)^3} = \\\\{\left( { - 14} \right)^3}\end{array}\)

\({\left( {\frac{2}{3}} \right)^0} \times {\left( {\frac{2}{3}} \right)^7} = {\left( {\frac{2}{3}} \right)^7}\)

درست می باشد؛ زیرا:

\({\left( {\frac{2}{3}} \right)^0} \times {\left( {\frac{2}{3}} \right)^7} = {\left( {\frac{2}{3}} \right)^{0 + 7}} = {\left( {\frac{2}{3}} \right)^7}\)

البته به صورت دیگری هم می توان درستی تساوی بالا را نشان داد:

\({\left( {\frac{2}{3}} \right)^0} \times {\left( {\frac{2}{3}} \right)^7} = 1 \times {\left( {\frac{2}{3}} \right)^7} = {\left( {\frac{2}{3}} \right)^7}\)

\(\frac{2}{3} \times \frac{2}{3} \times \frac{2}{3} = {\left( {\frac{2}{3}} \right)^3}\)

\(\frac{{2 + 2 + 2}}{3} = \frac{6}{3} = 2\)

\(\frac{{3 \times 2}}{3} = \frac{6}{3} = 2\)

\(\frac{2}{3} \times 3 = \frac{6}{3} = 2\)

\(\frac{2}{3} + \frac{2}{3} + \frac{2}{3} = \frac{{2 + 2 + 2}}{3} = \frac{6}{3} = 2\)

\(\frac{2}{3} + 3 = \frac{2}{3} + \frac{9}{3} = \frac{{11}}{3}\)

بنابراین \(\frac{2}{3} \times \frac{2}{3} \times \frac{2}{3}\) برابر با عبارت \({\left( {\frac{2}{3}} \right)^3}\) می باشد.

الف

\(\begin{array}{l}4096 \times 65536 = {4^6} \times {4^8} = \\\\{4^{6 + 8}} = {4^{14}}\end{array}\)

ب

\(\begin{array}{l}{4^{10}} = {4^5} \times {4^5} = 1,024 \times 1,024\\\\ \Rightarrow 1000 < {4^5} < 1100\\\\ \Rightarrow 1,000 \times 1,000 < {4^5} \times {4^5} < 1,100 \times 1,100\\\\ \Rightarrow 1,000,000 < {4^{10}} < 1,210,000\end{array}\)

عدد \({4^{10}}\) بین دو عدد 1,000,000 و 1,210,000 می باشد. این دو عدد 7 رقمی هستند؛ بنابراین عدد \({4^{10}}\) نیز 7 رقمی می باشد.

حال به همین صورت عمل می کنیم و بررسی می کنیم که عدد \({4^{20}}\) چند رقمی می باشد:

\(\begin{array}{l}{4^{20}} = {4^{10}} \times {4^{10}}\\\\ \Rightarrow 1000 < {4^5} < 1100\\\\ \Rightarrow 1,000 \times 1,000 < {4^5} \times {4^5} < 1,100 \times 1,100\\\\ \Rightarrow {(1,000)^2} < {4^{10}} < {(1,100)^2}\\\\ \Rightarrow {(1,000)^2} \times {(1,000)^2} < {4^{10}} \times {4^{10}} < {(1,100)^2} \times {(1,100)^2}\\\\ \Rightarrow {(1,000)^4} < {4^{20}} < {(1,100)^4}\\\\{(1,000)^4} = 1,000,000,000,000\\\\{(1,100)^4} = 1,464,100,000,000\end{array}\)

عدد \({4^{20}}\) بین دو عدد 1,000,000,000,000 و 1,464,100,000,000 می باشد. این دو عدد 13 رقمی هستند؛ بنابراین عدد \({4^{20}}\) نیز 13 رقمی می باشد.

الف

\(\begin{array}{l}{3^2} - {1^2} = {\left( {} \right)^3}\\\\{3^2} - {1^2} = 9 - 1 = 8 = {2^3}\\\\ \Rightarrow {3^2} - {1^2} = {\left( 2 \right)^3}\end{array}\)

\(\begin{array}{l}{6^2} - {3^2} = {\left( {} \right)^3}\\\\36 - 9 = 27 = {\left( 3 \right)^3}\\\\ \Rightarrow {6^2} - {3^2} = {\left( 3 \right)^3}\end{array}\)

\(\begin{array}{l}{10^2} - {6^2} = {\left( {} \right)^3}\\\\100 - 36 = 64 = {\left( 4 \right)^3}\\\\ \Rightarrow {10^2} - {6^2} = {\left( 4 \right)^3}\end{array}\)

\(\begin{array}{l}{15^2} - {10^2} = {\left( {} \right)^3}\\\\225 - 100 = 125 = {\left( 5 \right)^3}\\\\ \Rightarrow {15^2} - {10^2} = {\left( 5 \right)^3}\end{array}\)

\(\begin{array}{l}{21^2} - {15^2} = {\left( {} \right)^3}\\\\441 - 225 = 216 = {\left( 6 \right)^3}\\\\ \Rightarrow {21^2} - {15^2} = {\left( 6 \right)^3}\end{array}\)

با پر کردن جاهای خالی، الگوی بدست آمده به این صورت می شود که در تمام عبارت های فوق، پایه ها از هم کم شده اند و یک واحد به توان اضافه می شود؛ برای نمونه به مثال زیر توجه کنید:

\({21^2} - {15^2} = {(21 - 15)^{2 + 1}} = {(6)^3}\)

ب

خیر، درست می باشد؛ زیرا:

\(\begin{array}{l}{3^3} - {1^3} = {2^4}\\\\\left\{ \begin{array}{l}{3^3} - {1^3} = 27 - 1 = 26\\\\{2^4} = 16\end{array} \right.\\\\ \Rightarrow {3^3} - {1^3} \ne {2^4}\end{array}\)

\(\begin{array}{l}{2^5}\;\bigcirc \;8 = 4\\\\32\;\bigcirc \;8 = 4 \Rightarrow \bigcirc \equiv \div \\\\ \Rightarrow {2^5}\; \div \;8 = 4\end{array}\)

\(\begin{array}{l}{3^2}\;\bigcirc \;{7^2} = 58\\\\9\;\bigcirc \;49 = 58 \Rightarrow \bigcirc \equiv + \\\\ \Rightarrow 9\; + \;49 = 58\end{array}\)

\(\begin{array}{l}{\left( { - 7} \right)^0}\;\bigcirc \;{8^1} = {3^2}\\\\1\;\bigcirc \;8 = 9 \Rightarrow \bigcirc \equiv + \\\\{\left( { - 7} \right)^0}\; + \;{8^1} = {3^2}\end{array}\)

\(\begin{array}{l}{2^6}\;\bigcirc \;16 = {2^0}\;\Delta \;{2^2}\\\\64\bigcirc \;16 = 1\;\Delta \;4 \Rightarrow \left\{ \begin{array}{l}\bigcirc \equiv \div \\\\\Delta \equiv \times \end{array} \right.\\\\ \Rightarrow {2^6}\; \div \;16 = {2^0}\; \times \;{2^2}\end{array}\)