شاه کلید نکات
شاه کلید سوال
1 الف مسیر رفتن از نقطه A به B را به صورت زیر بیان کنید:
_____ واحد در جهت _____ محور xها و _____ واحد در جهت _____ محور yها
ب مختصات بردار AB را بنویسید. \(\overrightarrow {AB} = \left[ \begin{array}{l}\\\end{array} \right]\)
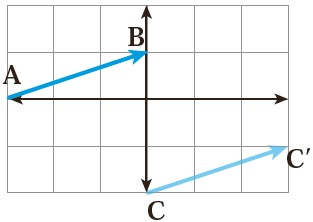
پ با همین بردار نقطه C را به نقطه ′C منتقل کردیم. مختصات بردار ′CC را مشخص کنید.
الف
3 واحد در جهت مثبت محور xها و 1 واحد در جهت مثبت محور yها
ب
\(\overrightarrow {AB} = \left[ \begin{array}{l}3\\1\end{array} \right]\)
پ
به دلیل اینکه نقطۀ C بوسیلۀ بردار AB به نقطۀ C’ منتقل شده است، پس خواهیم داشت:
\(\overrightarrow {CC'} = \overrightarrow {AB} = \left[ \begin{array}{l}3\\1\end{array} \right]\)
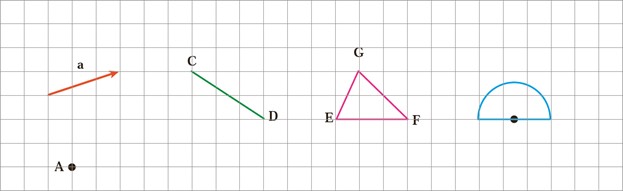
2 هر یک از شکل های زیر را با بردار \(\overrightarrow a \) منتقل کنید (هم راستا، هم جهت و هم اندازه حرکت کنید.)
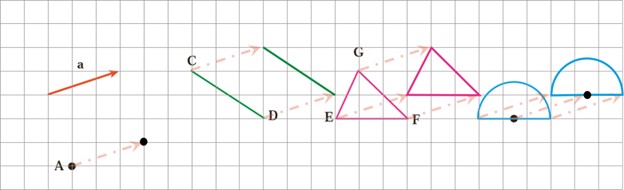
3 در محور مختصات زیر مثلث ABC را با بردار a انتقال دهید و مثلث جدید را ′A′ B′ C بنامید. مختصات رأس ها را بنویسید.
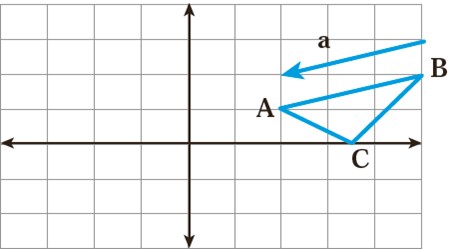
\(\begin{array}{l}A = \left[ \begin{array}{l}\\\end{array} \right]\;\;\;B = \left[ \begin{array}{l}\\\end{array} \right]\;\;\;C = \left[ \begin{array}{l}\\\end{array} \right]\\\\A' = \left[ \begin{array}{l}\\\end{array} \right]\;\;\;B' = \left[ \begin{array}{l}\\\end{array} \right]\;\;\;C' = \left[ \begin{array}{l}\\\end{array} \right]\end{array}\)
مختصات بردار انتقال a را هم بنویسید: \(\overrightarrow a = \left[ \begin{array}{l}\\\end{array} \right]\) چه رابطه ای بین رأس های مثلث، قبل و بعد از انتقال وجود دارد؟
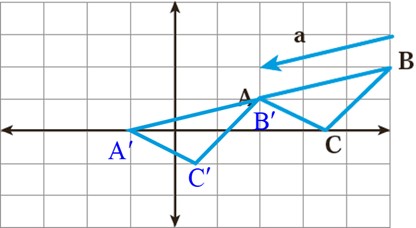
\(\begin{array}{l}A = \left[ \begin{array}{l}2\\1\end{array} \right]\;\;\;B = \left[ \begin{array}{l}5\\2\end{array} \right]\;\;\;C = \left[ \begin{array}{l}3/5\\0\end{array} \right]\\\\A' = \left[ \begin{array}{l} - 1\\0\end{array} \right]\;\;\;B' = \left[ \begin{array}{l}2\\1\end{array} \right]\;\;\;C' = \left[ \begin{array}{l}0/5\\ - 1\end{array} \right]\\\\\overrightarrow a = \left[ \begin{array}{l} - 3\\ - 1\end{array} \right]\end{array}\)
همۀ رأس های مثلث انتقال یافته به اندازه 3 واحد از طول و یک واحد از عرض رأس های مثلث اول کمتر هستند:
\(\begin{array}{l}A = \left[ \begin{array}{l}2\\1\end{array} \right]\,\,\,\,\,\mathop \Rightarrow \limits^{\overrightarrow a = \left[ {\scriptstyle - 3\atop\scriptstyle - 1} \right]} \,\,\,\,\,A' = \left[ \begin{array}{l}2 - 3\\1 - 1\end{array} \right] = \left[ \begin{array}{l} - 1\\0\end{array} \right]\\\\B = \left[ \begin{array}{l}5\\2\end{array} \right]\,\,\,\,\,\mathop \Rightarrow \limits^{\overrightarrow a = \left[ {\scriptstyle - 3\atop\scriptstyle - 1} \right]} \,\,\,\,\,B' = \left[ \begin{array}{l}5 - 3\\2 - 1\end{array} \right] = \left[ \begin{array}{l}2\\1\end{array} \right]\\\\C = \left[ \begin{array}{l}3/5\\0\end{array} \right]\,\,\,\,\,\mathop \Rightarrow \limits^{\overrightarrow a = \left[ {\scriptstyle - 3\atop\scriptstyle - 1} \right]} \,\,\,\,\,C' = \left[ \begin{array}{l}3/5 - 3\\0 - 1\end{array} \right] = \left[ \begin{array}{l}0/5\\ - 1\end{array} \right]\end{array}\)
4 برای هر یک از بردارهای زیر مختصات ابتدا و انتهای بردار را بنویسید.
چه رابطه ای بین ابتدا و انتها و مختصات بردار وجود دارد؟ این بردارها چه ویژگی دیگری دارند؟
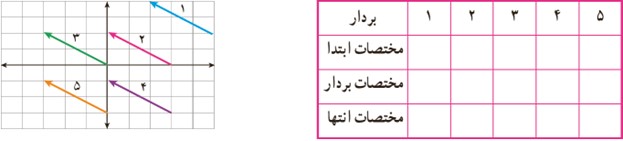
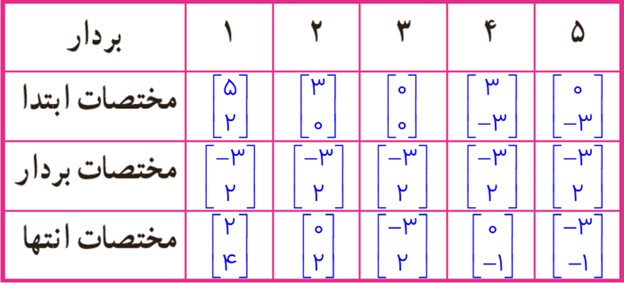
مختصات بردار + مختصات ابتدا = مختصات انتها
همگی بردارها، هم راستا، هم جهت و هم اندازه هستند و همگی بردار \(\left[ {\begin{array}{*{20}{c}}{ - 3}\\2\end{array}} \right]\) را نمایش می دهند.
1736019749.png)
