شاه کلید نکات
شاه کلید سوال
1 مسیر حرکت از A به B، به C، به D، و به E را با بردارهای انتقال مشخص کنید و مختصات هر بردار را بنویسید.
می توانید این بازی را به صورت دونفره انجام دهید. یک نفر نقطه می گذارد و نفر دوم باید بگوید با چه بردار انتقالی نقطه شروع را به نقطه مشخص شده، انتقال می دهد.
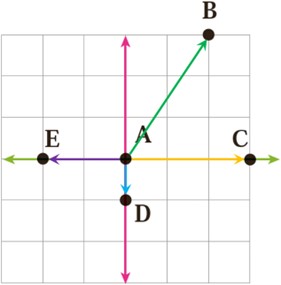
\(\begin{array}{l}\overrightarrow {AB} = \left[ {\begin{array}{*{20}{c}}2\\3\end{array}} \right]\\\\\overrightarrow {AC} = \left[ {\begin{array}{*{20}{c}}3\\0\end{array}} \right]\\\\\overrightarrow {AD} = \left[ {\begin{array}{*{20}{c}}0\\{ - 1}\end{array}} \right]\\\\\overrightarrow {AE} = \left[ {\begin{array}{*{20}{c}}{ - 2}\\0\end{array}} \right]\end{array}\)
2 بردارهای مساوی را مشخص کنید.
\(\begin{array}{l}w = x = l = \left[ {\begin{array}{*{20}{c}}0\\{ - 4}\end{array}} \right]\\\\t = z = \left[ {\begin{array}{*{20}{c}}{ - 3}\\2\end{array}} \right]\\\\u = v = \left[ {\begin{array}{*{20}{c}}3\\1\end{array}} \right]\end{array}\)
3 الف بردار قرینه هر بردار را بکشید و تساوی ها را کامل کنید.
\(\overrightarrow d = \left[ \begin{array}{l}\\\end{array} \right]\; \Rightarrow \;\overrightarrow d ' = \left[ \begin{array}{l}\\\end{array} \right]\)
ب چگونه مختصات قرینه یک بردار نوشته می شود؟
پ با توجه به شکل بالا حاصل عبارت مقابل را به دست آورید.
\(\overrightarrow d + \overrightarrow d ' = \left[ \begin{array}{l}\\\end{array} \right]\; + \left[ \begin{array}{l}\\\end{array} \right] = \left[ \begin{array}{l}\\\end{array} \right]\)
الف
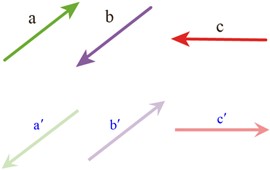
\(\overrightarrow d = \left[ \begin{array}{l}4\\ - 2\end{array} \right]\; \Rightarrow \;\overrightarrow d ' = \left[ \begin{array}{l} - 4\\2\end{array} \right]\)
ب
برای به دست آوردن مختصات قرینۀ یک بردار، کافی است هر دو مؤلفه آن را قرینه کنیم:
\(\overrightarrow d = \left[ \begin{array}{l}4\\ - 2\end{array} \right]\; \Rightarrow \;\overrightarrow d ' = \left[ \begin{array}{l} - ( - 4)\\ - ( - 2)\end{array} \right] = \left[ \begin{array}{l} - 4\\2\end{array} \right]\)
پ
\(\overrightarrow d + \overrightarrow d ' = \left[ \begin{array}{l}4\\ - 2\end{array} \right]\; + \left[ \begin{array}{l} - 4\\2\end{array} \right] = \left[ \begin{array}{l}0\\0\end{array} \right]\)
4 در محور مختصات زیر در کاشی شمارهٔ n مختصات گوشه ای را که با علامت \(\bigcirc \) مشخص شده است، به صورت جبری بنویسید.
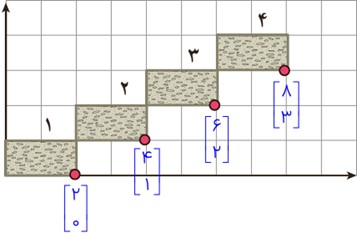
\(\begin{array}{*{20}{c}}1&2&3&4&{}&n\\{\left[ {\begin{array}{*{20}{c}}2\\0\end{array}} \right]}&{\left[ {\begin{array}{*{20}{c}}4\\1\end{array}} \right]}&{\left[ {\begin{array}{*{20}{c}}6\\2\end{array}} \right]}&{\left[ {\begin{array}{*{20}{c}}8\\3\end{array}} \right]}&{}&{\left[ {\begin{array}{*{20}{c}}{2n}\\{n - 1}\end{array}} \right]}\end{array}\)
5 در یک بازی روی صفحه شطرنجی، سعید مهره خود را از خانه ای به مختصات \(\left[ \begin{array}{l} - 2\\\;3\end{array} \right]\) ابتدا 3 خانه به سمت راست و سپس 4 خانه به سمت پایین آورد. در حرکت دوم او مهره اش را 2 خانه به سمت چپ آورد. هم اکنون مهره سعید روی کدام نقطه صفحه قرار دارد؟
ابتدا بردار 3 خانه به سمت راست و 4 خانه به سمت پایین را می نویسیم:
\(\overrightarrow a = \left[ {\begin{array}{*{20}{c}}3\\{ - 4}\end{array}} \right]\)
حال بردار بعدی را که 2 خانه به سمت چپ هست می نویسیم:
\(\overrightarrow b = \left[ {\begin{array}{*{20}{c}}{ - 2}\\0\end{array}} \right]\)
حال بردار برآیند را که از جمع این دو بردار بدست می آید، را می یابیم:
\(\overrightarrow c = \overrightarrow a + \overrightarrow b = \left[ {\begin{array}{*{20}{c}}3\\{ - 4}\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}{ - 2}\\0\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}1\\{ - 4}\end{array}} \right]\)
حال مختصات نقطه نهایی را به کمک مختصات نقطه ابتدایی و این بردار برآیند بدست آمده، می یابیم:
\(\begin{array}{l}A = \left[ {\begin{array}{*{20}{c}}{ - 2}\\3\end{array}} \right]\,\,\,\,\,\mathop \Rightarrow \limits^{\overrightarrow c = \left[ {\begin{array}{*{20}{c}}1\\{ - 4}\end{array}} \right]} \,\,\,\,\,A' = \left[ {\begin{array}{*{20}{c}}{ - 2 + 1}\\{3 + ( - 4)}\end{array}} \right]\\\\ \Rightarrow A' = \left[ {\begin{array}{*{20}{c}}{ - 1}\\{ - 1}\end{array}} \right]\end{array}\)
6 اگر نقطه A به مختصات \(\left[ \begin{array}{l}x\\y\end{array} \right]\) را با بردار انتقال \(\left[ \begin{array}{l}a\\b\end{array} \right]\) منتقل کنیم تا به نقطه B برسیم، مختصات نقطه B را به صورت جبری بنویسید.
مختصات بردار + مختصات ابتدا = مختصات انتها
\(B = \left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}a\\b\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{x + a}\\{y + b}\end{array}} \right]\)
1736019749.png)
