آیا تمام سوالات فعالیت صفحه 68 ریاضی دوازدهم تجربی، مطابق با آخرین تغییرات کتب درسی پاسخ داده شده است ؟

بله، تمام جواب ها به فعالیت صفحه 68 ریاضی دوازدهم تجربی مطابق با آخرین تغییرات کتب درسی 1402 - 1401 است.

آیا جواب ها به صورت آموزش محور و کامل بیان شده اند ؟

بله، جواب سوالات به صورت کاملا تشریحی و با هدف یادگیری و تسلط به مبحث بیان شده اند.

جواب فعالیت صفحه 68 درس 4 ریاضی دوازدهم تجربی (مشتق)

تعداد بازدید : 78.78M

پاسخ فعالیت صفحه 68 ریاضی دوازدهم تجربی

گام به گام فعالیت صفحه 68 درس مشتق

فعالیت صفحه 68 درس 4

شما در حال مشاهده جواب فعالیت صفحه 68 ریاضی دوازدهم تجربی هستید. ما در تیم مای درس، پاسخ‌نامه‌های کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کرده‌ایم. اگر به دنبال به‌روزترین پاسخ‌ها برای این صفحه هستید و می‌خواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخ‌های گام به گام، به گنجینه‌ای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مای‌درس را نصب نمایید.

الف تابع \(f\left( x \right) = - {x^2} + 10x\) داده شده است، اگر \(0 \le x \le 10\) نقاط \(A(2,f(2)) \)، \(B(6,f(6))\)، \(C(5,f(5))\)، \(D(4,f(4))\) و \(E(3,f(3))\) را روی منحنی در نظر می گیریم. شیب خطی که از نقاط A و B می گذرد یعنی m_AB از دستور زیر به دست می آید:

\({m_{AB}} = \frac{{{v_B} - {v_A}}}{{{x_B} - {x_A}}} = \frac{{f\left( 6 \right) - f\left( 2 \right)}}{{6 - 2}} = \frac{{24 - 16}}{4} = \frac{8}{4} = 2\)

به همین روش m_AC و m_AD و m_AE را به دست آورید.

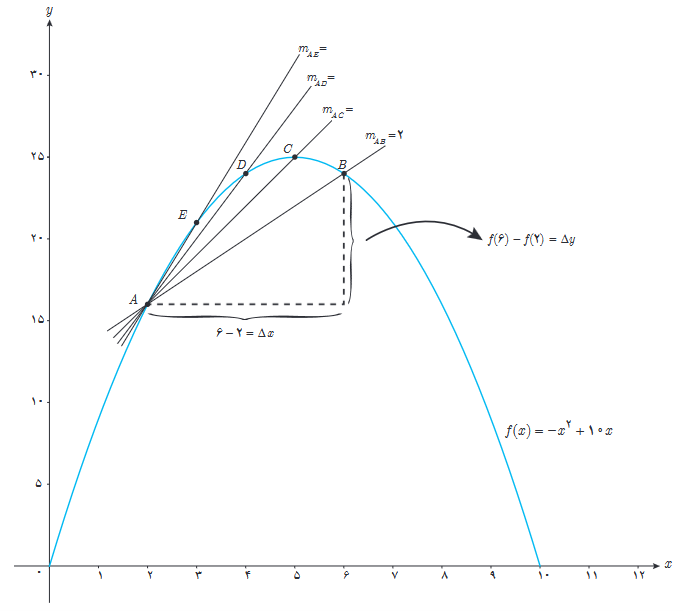
\(\begin{array}{l}A\left| {\begin{array}{*{20}{c}}2\\{16}\end{array}\quad ,\quad } \right.B\left| {\begin{array}{*{20}{c}}6\\{24}\end{array}\quad ,\quad } \right.C\left| {\begin{array}{*{20}{c}}5\\{25}\end{array}\quad ,\quad D} \right.\left| {\begin{array}{*{20}{c}}4\\{24}\end{array}\quad ,\quad E} \right.\left| {\begin{array}{*{20}{c}}3\\{21}\end{array}} \right.\\\\{m_{AC}} = \frac{{{y_C} - {y_A}}}{{{x_C} - {x_A}}} = \frac{{25 - 16}}{{5 - 2}} = \frac{9}{3} = 3\\\\{m_{AD}} = \frac{{{y_D} - {y_A}}}{{{x_D} - {x_A}}} = \frac{{24 - 16}}{{4 - 2}} = \frac{8}{2} = 4\\\\{m_{AE}} = \frac{{{y_E} - {y_A}}}{{{x_E} - {x_A}}} = \frac{{21 - 16}}{{3 - 2}} = \frac{5}{1} = 5\end{array}\)

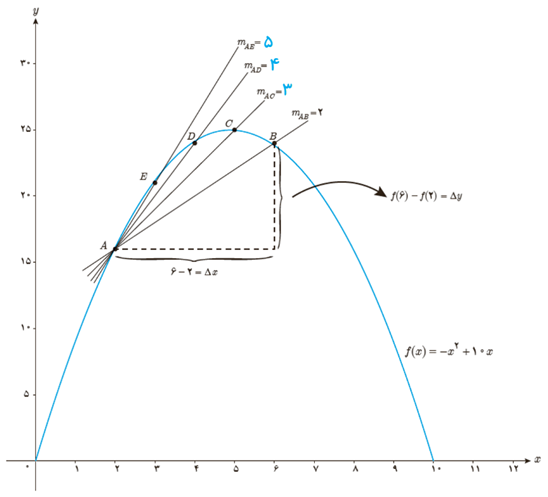
همان طور که می دانید برای محاسبه شیب خط AB نسبت تغییر عمودی را به تغییر افقی به دست می آوریم. اگر این تغییرات را به ترتیب با Δy و Δx نمایش دهیم، داریم:

\({m_{AB}} = \frac{{\Delta y}}{{\Delta x}}\)

در هنگام محاسبه شیب های بالا، توضیح دهید که Δxها چگونه تغییر می کنند؟

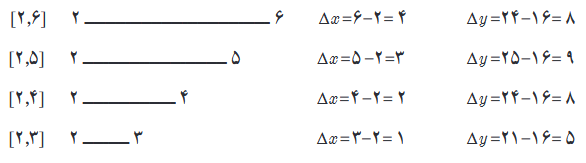
مقدارشان کوچکتر می شود.

ب حال فرض کنید که با ادامه روندی که در قسمت (الف) اختیار کردیم، نقاط بیشتری را نزدیک به A انتخاب کنیم. شیب خطوط به دست آمده به شیب خط مماس بر منحنی در نقطه A نزدیک می شود. برای درک بهتر این موضوع، منحنی \(f\left( x \right) = - {x^2} + 10x\) در فاصله [2,3] رسم شده است. در ادامه نمودار تابع در بازه [2,2/4] رسم شده است.

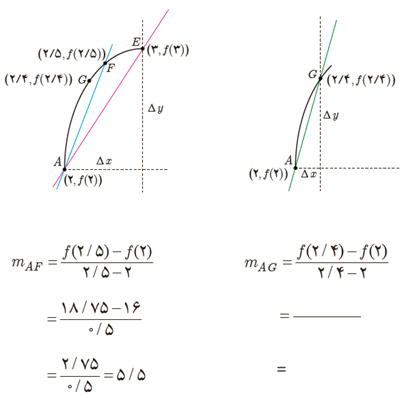
\(\begin{array}{l}{m_{AG}} = \frac{{f(2/4) - f(2)}}{{2/4 - 2}}\\\\ = \frac{{18/25 - 16}}{{2/4 - 2}} = \frac{{2/25}}{{0/4}}\\\\ = 5/625\end{array}\)

اگر به همین ترتیب بازه های کوچک تری در نظر بگیریم، شیب خطوط به دست آمده به شیب خط مماس بر منحنی در نقطه A نزدیک می شود. برای درک بهتر این موضوع، با تکمیل جدول و مقایسه شیب خط های قاطع، شیب خط مماس را حدس بزنید.