جواب مرور فصل 2 صفحه 26 درس 2 ریاضی هفتم (عددهای صحیح)

1 عدد علامت دار

عددهایی هستند که که دارای علامت های مثبت و منفی هستند. به این اعداد، اعداد علامتدار می گوییم. اعداد علامتدار مانند:

1+ که یعنی یک واحد بزرگ تر از صفر؛ همان طور که می بینیم در عدد علامتدار 1+، ابتدا علامت + نوشته می شود و سپس در سمت راست آن، عدد 1 می آید.

حال یکی دیگر از عددهای علامتدار را مثال می زنیم:

3- که یعنی 3 واحد کوچک تر از صفر؛ همان طور که می بینیم در عدد علامتدار 3-، ابتدا علامت – نوشته می شود و سپس در سمت چپ آن، عدد 3 می آید.

بیاییم مثال های دیگری برای اعداد علامتدار بنویسیم:

5+ یعنی 5 واحد بزرگ تر از صفر.

7- یعنی 7 واحد کوچک تر از صفر.

100+ یعنی 100 واحد بزرگ تر از صفر.

200- یعنی 200 واحد کوچک تر از صفر.

به اعداد علامتداری که علامت آن ها + باشد، اعداد مثبت و به اعداد علامتداری که علامت آن ها – باشد، اعداد منفی می گوییم. در مثال های بالا، اعداد 1+، 5+ و 100+ همگی اعداد مثبت و 3-، 7- و 200- همگی اعداد منفی می باشند.

2 عدد صحیح

اگر اعداد علامتدار مثبت و عدد صفر و اعداد علامتدار منفی را بخواهیم در یک دسته بنویسیم، اعداد صحیح بوجود می آید. همان طور که گفتیم، این اعداد از سه قسمت تشکیل می شوند:

الف اعداد مثبت که بزرگتر از صفر هستند.

ب عدد صفر

پ اعداد منفی که کوچکتر از صفر هستند.

اعداد صحیح را با نماد Z نوشته و آن را به صورت زیر نمایش می دهیم:

\(\mathbb{Z} = \{ \cdots \,,\, - 3\,,\, - 2\,,\, - 1\,,\,0\,,\, + 1\,,\, + 2\,,\, + 3\,,\, \cdots \} \)

3 قرینهٔ عدد

هنگامی که علامت سمت چپ عددی را تغییر دهیم، می گوییم قرینۀ آن عدد را بدست آورده ایم؛ مثلاً قرینۀ عدد 1+ برابر 1- است یا قرینه عدد 5-، عدد 5+ می باشد. همچنین چون اعداد بدون علامت همان عدد مثبت هستند، مثلاً 5 همان 5+ است، پس قرینه عدد 5 هم 5- می شود.

4 گستردهٔ عدد صحیح

برای نوشتن گسترده هر عدد صحیح بایستی به دو مورد توجه کنیم:

الف علامت عدد

ب ارزش مکانی هر رقم در عدد مورد نظر

به عنوان مثال، گسترده اعداد زیر را نوشته ایم تا نحوه کار را یاد بگیریم:

\(\begin{array}{l}3125 = 3 \times 1000 + 1 \times 100 + 2 \times 10 + 5\\\\ - 75 = - (7 \times 10 + 5 \times 1) = - (70 + 5) = - 70 - 5 = ( - 70) + ( - 5)\end{array}\)

۱ قراردادی برای جهت‌های مثبت و منفی

این مفهوم، اساس زبان عددهای صحیح است. ما در طبیعت با مفاهیم متضاد روبرو هستیم: گرما و سرما، بالا و پایین، سود و زیان. برای اینکه بتوانیم این تضادها را در ریاضی نشان دهیم، یک جهت را مثبت (+) و جهت مخالف آن را منفی (-) در نظر می‌گیریم.

مثال: در هواشناسی، دمای بالای صفر را با علامت مثبت و دمای زیر صفر را با علامت منفی نشان می‌دهیم. دمای «۳ درجه بالای صفر» به صورت 3+ و دمای «۶ درجه زیر صفر» به صورت 6- نوشته می‌شود.

۲ محور عددهای صحیح و مرتب کردن آن‌ها

همچنان که اعداد طبیعی و حسابی را می توانیم بر روی محور نمایش دهیم، برای نمایش اعداد صحیح نیز می توانیم از محور اعداد استفاده کنیم:

عدد صفر را به عنوان مبدأ در نظر می گیریم. سمت راست صفر را با اعداد صحیح مثبت و سمت چپ صفر را با اعداد صحیح منفی نمایش می دهیم.

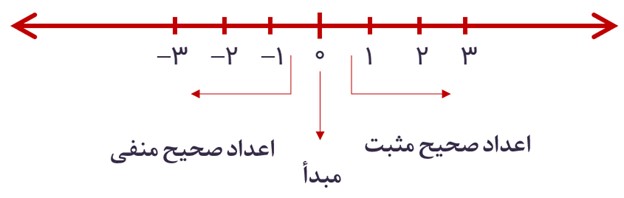
بر روی محور اعداد، هر چه به سمت راست حرکت کنیم، اعداد بزرگتر می شوند و هر چه به سمت چپ حرکت کنیم، اعداد کوچکتر می شوند. مثلاً عدد 2+ از عدد 5- بزرگتر است؛ زیرا این عدد بر روی محور اعداد صحیح در سمت راست 5- قرار می گیرد. همچنین عدد 10- از عدد 5- کوچکتر است؛ زیرا این عدد در سمت چپ 5- قرار می گیرد.

نکته

الف عدد صفر کوچکتر از همه اعداد مثبت و بزرگتر از تمام اعداد منفی می باشد.

ب تمام اعداد صحیح مثبت از تمام عددهای منفی بزرگتر هستند.

پ عددهایی که دارای اعشار هستند، مانند 0/32 یا 10/24- و همچنین کسرهایی مانند \( + 5\frac{1}{4}\) یا \( - 3\frac{1}{3}\) که نشان دهنده واحد کامل بر روی محور اعداد نیستند، عدد صحیح نمی باشند.

مثال: حال با این توضیحاتی که دادیم می خواهیم اعداد صحیح زیر را از کوچک به بزرگ مرتب کنیم:

\( - 1{\rm{ }},{\rm{ }} + 6{\rm{ }},{\rm{ }} + 3{\rm{ }},{\rm{ }} - 2{\rm{ }},{\rm{ }} - 3{\rm{ }},{\rm{ }} - 10{\rm{ }},{\rm{ }} + 11\)

می دانیم که اعداد مثبت از صفر و از اعداد منفی بزرگتر هست و همچنین بر روی محور اعداد صحیح، عددی که در سمت راست عددی دیگر قرار می گیرد، از آن بزرگتر است. بنابراین ابتدا اعداد بالا را بر روی محور اعداد صحیح مشخص می کنیم:

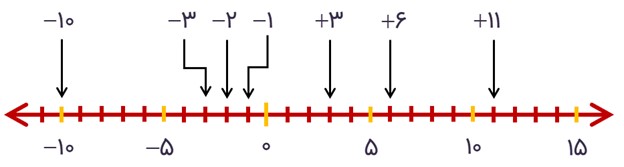
بنابراین داریم:

\( - 10 < - 3 < - 2 < - 1 < + 3 < + 6 < + 11\)

در نتیجه ترتیب اعداد صحیح از کوچک به بزرگ به صورت زیر می شود:

\( - 10{\rm{ }},{\rm{ }} - 3{\rm{ }},{\rm{ }} - 2{\rm{ }},{\rm{ }} - 1{\rm{ }},{\rm{ }} + 3{\rm{ }},{\rm{ }} + 6{\rm{ }},{\rm{ }} + 11\)

۳ قرینهٔ قرینهٔ یک عدد صحیح

قرینه قرینه هر عدد، خود آن عدد است.

مثال:

\(\begin{array}{l} - ( - ( + 1)) = - ( - 1) = + 1\\\\ - ( - ( - 17)) = - ( + 17) = - 17\\\\ - ( - ( + 103)) = - ( - 103) = + 103\\\\ - ( - ( - 85)) = - ( + 85) = - 85\end{array}\)

۴ هر عدد صحیح مثبت، یک عدد طبیعی است

عددهای طبیعی همان عددهایی هستند که با آن‌ها شمارش را یاد گرفتی (۱, ۲, ۳, ...). عددهای صحیح مثبت دقیقاً معادل همین‌ها هستند. علامت مثبت (+) را می‌توانیم برای آن‌ها ننویسیم.

مثال: عدد صحیح 7+ همان عدد طبیعی 7 است. پس 7+ = 7

۵ تبدیل تفریق به جمع

این یک استراتژی هوشمندانه برای ساده کردن محاسبات است. به جای تفریق یک عدد، می‌توانیم قرینه آن عدد را جمع کنیم. این کار از بروز اشتباه جلوگیری می‌کند.

مثال: عبارت \( - 5 - ( - 2)\) را در نظر بگیر. برای حل، عمل تفریق را به جمع تبدیل کرده و قرینه عدد دوم 2- را که 2+ است، جایگزین می‌کنیم:

\( - 5 - ( - 2) = - 5 + ( + 2) = - 3\)

۶ جمع و تفریق روی محور

محور اعداد به ما کمک می‌کند تا حرکت ناشی از جمع و تفریق را ببینیم. برای عددهای مثبت به راست و برای عددهای منفی به چپ حرکت می‌کنیم.

مثال:

\(\left( { + 7} \right) + \left( { + 5} \right) = + 12\)

اگر بخواهیم هر دو حرکت را بر روی یک محور نشان دهید، به صورت زیر می شود:

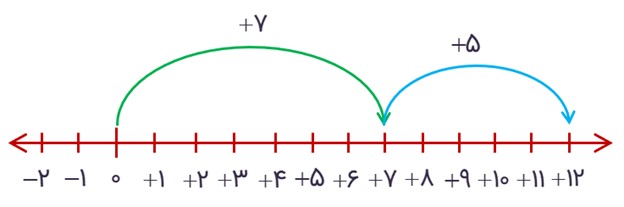
\(\left( { + 3} \right) + \left( { - 4} \right) = - 1\)

اگر بخواهیم هر دو حرکت را بر روی یک محور نشان دهید، به صورت زیر می شود:

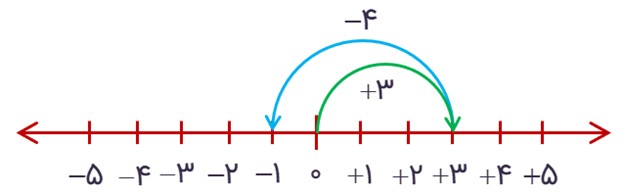
۷ جمع و تفریق با دایره‌های سیاه و سفید

این یک روش تصویری برای درک مفهوم خنثی شدن عددهای مثبت و منفی است. هر دایره سفید (⚪) را  1+ و هر دایره سیاه (⚫) را 1- در نظر می‌گیریم. یک جفت دایره سیاه و سفید، اثر هم را خنثی کرده و حاصلشان صفر می‌شود.

مثال: برای محاسبه \(( - 4) + ( + 2)\) دو دایره سفید (⚪⚪) و چهار دایره سیاه (⚫⚫⚫⚫) را کنار هم می‌گذاریم. دو جفت سیاه و سفید همدیگر را خنثی می‌کنند و چیزی که باقی می‌ماند، دو دایره سیاه (⚫⚫) است. پس حاصل  2- می‌شود.

۸ مقایسه و مرتب کردن عددهای صحیح

برای مقایسه دو عدد صحیح، موقعیت آن‌ها را روی محور اعداد در نظر می‌گیریم. عددی که در سمت راست قرار دارد، همیشه بزرگ‌تر است.

مثال: می‌خواهیم اعداد  \( - 5\,\,\,,\,\,\, + 2\,\,\,,\,\,\,0\,\,\,,\,\,\, - 1\) را مرتب کنیم. با نگاه به محور اعداد، ترتیب آن‌ها از کوچک به بزرگ (از چپ به راست) به این صورت است:

\( - 5\,\,\,,\,\,\, - 1\,\,\,,\,\,\,0\,\,\,,\,\,\, + 2\)

۹ جمع و تفریق دو عدد صحیح

پس از تمرین با محور و دایره، می‌توانیم قوانین کلی را استخراج کنیم:

جمع دو عدد هم‌علامت: عددها را بدون علامت با هم جمع کرده و همان علامت مشترک را برای حاصل قرار می‌دهیم.

مثال:

\(\begin{array}{l}( - 4) + ( - 8) = - (4 + 8) = - 12\\\\( + 5) + ( + 6) = + (5 + 6) = + 11\end{array}\)

جمع دو عدد با علامت مختلف: عددها را بدون علامت از هم کم کرده (بزرگ‌تر منهای کوچک‌تر) و علامت عددی را برای حاصل می‌گذاریم که مقدارش (بدون علامت) بزرگ‌تر بوده است.

مثال:

\(\begin{array}{l}( + 9) + ( - 4) = + (9 - 4) = + 5\\\\( - 12) + ( + 8) = - (12 - 8) = - 4\end{array}\)

(چون ۹ از ۴ بزرگ‌تر است، علامت حاصل مثبت شد. همچنین به این علت که عدد 12 از 8 بزرگتر می باشد، علامت حاصل منفی شد.)

۱۰ تعیین علامت در ضرب و تقسیم

قانون علامت‌ها در ضرب و تقسیم بسیار ساده و قطعی است:

حاصل ضرب یا تقسیم دو عدد هم‌علامت (هر دو مثبت یا هر دو منفی) مثبت است.

حاصل ضرب یا تقسیم دو عدد با علامت‌های مختلف، منفی است.

۱۱ ضرب و تقسیم دو عدد صحیح

برای انجام این عملیات، دو مرحله ساده را طی می‌کنیم:

الف ابتدا با استفاده از قانون بالا، علامت جواب را تعیین کن.

ب سپس، عددها را بدون در نظر گرفتن علامتشان در هم ضرب یا بر هم تقسیم کن.

مثال:

\(( - 8) \times ( + 3) = - 24\)

(علامت‌ها مختلف است پس منفی؛ ۸ ضربدر ۳ می‌شود ۲۴)

\(( - 14) \div ( - 7) = + 2\)

(علامت‌ها یکسان است پس مثبت؛ ۱۴ تقسیم بر ۷ می‌شود ۲)

۱۲ انجام عملیات به صورت ذهنی

وقتی بر قوانین بالا مسلط شدی، توانایی محاسبات ذهنی در تو شکوفا می‌شود. کلید موفقیت در این بخش، شکستن عملیات پیچیده به مراحل ساده‌تر و به کار بردن سریع قوانین علامت‌هاست.

مثال: برای محاسبه ذهنی \(:\,( - 20) + ( + 50) - 10\)

1 ابتدا \( - 20 + 50\) را حساب می‌کنیم که می‌شود 30+

2 سپس \( + 30 - 10\) را حساب می کنیم که می شود 20+

۱۳ انجام عملیات به صورت تقریبی و با ماشین حساب

تقریب زدن: برای اعداد بزرگ، می‌توانیم آن‌ها را به نزدیک‌ترین عدد رند گرد کنیم تا یک تخمین سریع از جواب به دست آوریم.

مثال: حاصل \(( - 127) + ( + 270)\) تقریباً برابر است با \(( - 100) + ( + 300) = + 200\) . این کار برای بررسی سریع درستی جواب بسیار مفید است.

ماشین حساب: برای محاسبات دقیق، از ماشین حساب استفاده می‌کنیم. برای وارد کردن اعداد منفی، معمولاً از کلید -/+ استفاده می‌شود.

۱۴ حل مسائل مربوط به عددهای صحیح

اینجاست که تمام مهارت‌های بالا به کار می‌آیند. مهم‌ترین قدم در حل یک مسئله، ترجمه درست عبارت‌های فارسی به زبان ریاضی (عبارت‌های جبری) است.

مثال: یک زیردریایی ۴۵۰ متر پایین‌تر از سطح دریا (450-) قرار دارد. زیردریایی دیگری ۱۵۰ متر بالاتر از آن است. موقعیت زیردریایی دوم کجاست؟

ترجمه به ریاضی: \( - 450 + 150\)

حل:

\( - 450 + 150 = - 300\)

پاسخ: زیردریایی دوم در عمق ۳۰۰ متری (۳۰۰ متر زیر سطح دریا) قرار دارد.

۱ دنیای اقتصاد و امور مالی

در حساب‌های بانکی و مسائل مالی، عددهای صحیح نقش کلیدی دارند.

سود و زیان: سود در یک معامله با عدد مثبت و زیان با عدد منفی نشان داده می‌شود.

موجودی حساب بانکی: واریز پول به حساب شما یک حرکت مثبت (+) و برداشت پول یک حرکت منفی (-) است. اگر موجودی شما منفی شود، به این معنی است که به بانک بدهکار هستید.

۲ سفر در زمان با خط تاریخ

مورخان از عددهای صحیح برای نمایش وقایع تاریخی روی یک محور زمان استفاده می‌کنند. معمولاً یک رویداد مهم به عنوان مبدأ (صفر) انتخاب می‌شود و وقایع قبل و بعد از آن با اعداد منفی و مثبت مشخص می‌شوند.

مثال: در تقویم میلادی، سال تولد حضرت مسیح (ع) به عنوان مبدأ در نظر گرفته می‌شود. اتفاقات قبل از میلاد با اعداد منفی و اتفاقات بعد از میلاد با اعداد مثبت نمایش داده می‌شوند.

۳ هیجان در دنیای ورزش

در بسیاری از ورزش‌ها برای نمایش آمار و عملکرد تیم‌ها یا بازیکنان از عددهای صحیح استفاده می‌شود.

تفاضل گل: در فوتبال، تفاضل گل یک تیم (تعداد گل‌های زده منهای گل‌های خورده) با یک عدد صحیح نشان داده می‌شود. تفاضل مثبت نشانه عملکرد هجومی خوب و تفاضل منفی نشانه ضعف دفاعی است.

امتیاز در گلف: در ورزش گلف، امتیاز بازیکنان نسبت به تعداد ضربات استاندارد (Par) سنجیده می‌شود. امتیاز کمتر از استاندارد با عدد منفی (مثلاً ۲- که بسیار خوب است) و امتیاز بیشتر با عدد مثبت (مثلاً ۱+ که خوب نیست) نشان داده می‌شود.

۴ کشف رازهای علم و فناوری

فیزیک و شیمی: در علم فیزیک، بارهای الکتریکی ذرات با اعداد صحیح بیان می‌شوند. الکترون‌ها بار منفی (۱-) و پروتون‌ها بار مثبت (۱+) دارند.

آسانسور و طبقات ساختمان: همانطور که در تمرین‌های کتاب دیدی، طبقات بالای همکف مثبت، طبقه همکف صفر و طبقات زیرین (پارکینگ) منفی هستند.

\(\begin{array}{l}( - 18 \div 2) \times ( - 3 - 7) + ( - 6) = \\\\( - 9) \times ( - 10) + ( - 6) = \\\\ + 90 + ( - 6) = + 84\end{array}\)

\(\begin{array}{l} - 8 - ( - 4) = - 8 + ( + 4) = \\\\ - (8 - 4) = - 4\end{array}\)

\(\begin{array}{l} - 16 - ( + 4) = - 16 + ( - 4) = \\\\ - (16 + 4) = - 20\end{array}\)

\( - 20 + 5 = - (20 - 5) = - 15\)

\(\begin{array}{l} - 100 + 20 - 4 = - 100 + 16 = \\\\ - (100 - 16) = - 84\end{array}\)

\( = - 2\) دمای هوای تبریز

\( = 3 \times ( - 2) = - 6\) دمای هوای اردبیل

\( = (( - 2) + ( - 6)) \div 2 = \) میانگین دمای هوای دو شهر

\(( - 8) \div 2 = - 4\)