جواب فعّالیت 4 صفحه 58 درس 3 هندسه دهم (چند ضلعی ها)
تعداد بازدید : 80.84Mپاسخ فعّالیت 4 صفحه 58 هندسه دهم
-گام به گام فعّالیت 4 صفحه 58 درس چند ضلعی ها
-فعّالیت 4 صفحه 58 درس 3
-شما در حال مشاهده جواب فعّالیت 4 صفحه 58 هندسه دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
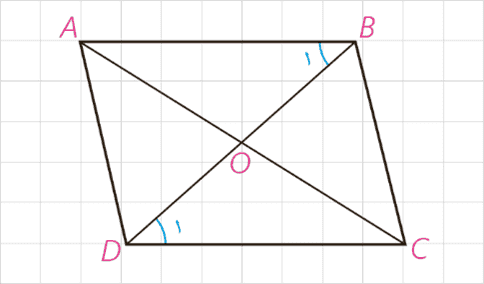
الف فرض کنید در یک چهارضلعی دو قطر منصف یکدیگر باشند. چگونه نشان می دهید این چهارضلعی متوازی الاضلاع است؟
ب نقطه تقاطع دو قطر را O می نامیم. \(\Delta AOB \cong \Delta OCD\). چرا؟
پ اندازه \(\angle {B_1}\) برابر اندازهٔ ……… است. در نتیجه، ضلع AB موازی ضلع .......... است. دو مثلث دیگر را درنظر بگیرید و به طور مشابه نشان دهید دو ضلع دیگر نیز موازی اند.
بنابراین؛
الف
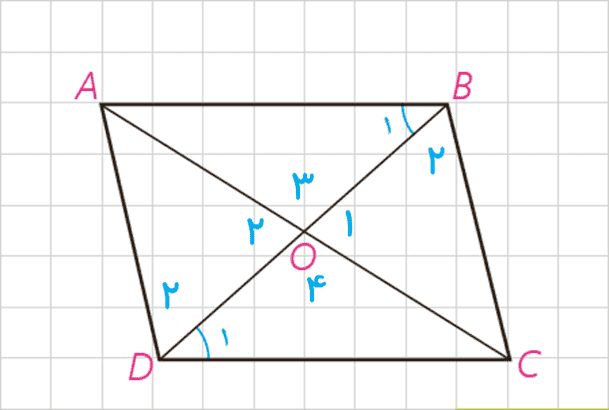
ابتدا موازی بودن دو ضلع AB و CD را نشان می دهیم:
AB=CD
متقابل به رأس \({\hat O_1} = {\hat O_2}\)
OB=OC
بنا به حالت (ض ز ض) \(\Rightarrow O\mathop A\limits^\Delta B \cong O\mathop C\limits^\Delta D\)
\(\Rightarrow {\hat B_1} = {\hat D_1} \Rightarrow AB||CD\)
حال موازی بودن دو ضلع AD و BC را نشان می دهیم:
AD=BC
متقابل به رأس \({\hat O_3} = {\hat O_4}\)
OD=OC
بنا به حالت (ض ز ض) \(\Rightarrow O\mathop A\limits^\Delta B \cong O\mathop C\limits^\Delta D\)
\(\Rightarrow {\hat B_2} = {\hat D_2} \Rightarrow AD||BC\)
در نتیجه به این دلیل که اضلاع چهارضلعی ABCD دو به دو با یکدیگر موازی هستند، این چهارضلعی یک متوازی الاضلاع می باشد.
ب
AB=CD
متقابل به رأس \({\hat O_1} = {\hat O_2}\)
OB=OC
بنا به حالت (ض ز ض) \(\Rightarrow O\mathop A\limits^\Delta B \cong O\mathop C\limits^\Delta D\)
پ اندازه \(\angle {B_1}\) برابر اندازهٔ …\({\widehat D_1}\)… است. در نتیجه، ضلع AB موازی ضلع ...CD... است. دو مثلث دیگر را درنظر بگیرید و به طور مشابه نشان دهید دو ضلع دیگر نیز موازی اند.
به روش مشابه ثابت می شود:
AD=BC
متقابل به رأس \({\hat O_3} = {\hat O_4}\)
OD=OC
بنا به حالت (ض ز ض) \(\Rightarrow O\mathop A\limits^\Delta B \cong O\mathop C\limits^\Delta D\)
\(\Rightarrow {\hat B_2} = {\hat D_2} \Rightarrow AD||BC\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















