جواب کار در کلاس صفحه 35 درس 2 هندسه دهم (قضیۀ تالس، تشابه و کاربردهای آن)
تعداد بازدید : 80.73Mپاسخ کار در کلاس صفحه 35 هندسه دهم
-گام به گام کار در کلاس صفحه 35 درس قضیۀ تالس، تشابه و کاربردهای آن
-کار در کلاس صفحه 35 درس 2
-شما در حال مشاهده جواب کار در کلاس صفحه 35 هندسه دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
در شکل مقابل، با فرض MN||BC، طبق قضیهٔ تالس داریم: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) حال عکس قضیهٔ تالس را به زبان ریاضی بنویسید.
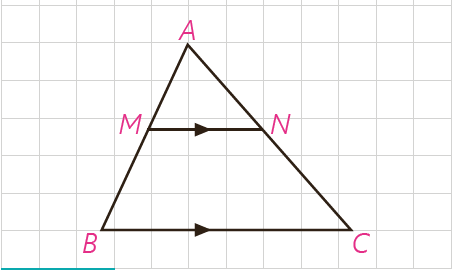
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\;\; \Rightarrow \;\;MN||BC\)
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) : فرض کنیم بر خلاف حکم MN موازی BC نیست. پس از نقطهٔ M پاره خط MN’ را موازی BC رسم می کنیم. حال با توجه به قضیهٔ تالس داریم:
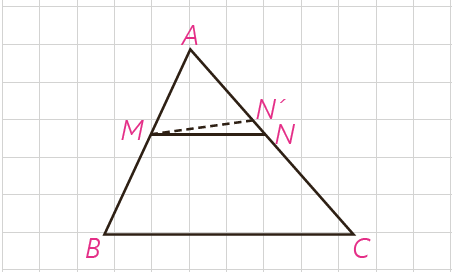
\(MN'||BC\; \Rightarrow \;\frac{{AN'}}{{AC}} = \frac{{\;....\;}}{{\;....\;}}\)
از مقایسهٔ این تناسب، با فرض مسئله نتیجه می شود \(\frac{{\;......\;}}{{\;......\;}} = \frac{{\;......\;}}{{\;......\;}}\) و در نتیجه: AN’=AN و بنابراین N بر N’ منطبق است و MN همان MN’ است که موازی BC است.
\(MN'||BC\; \Rightarrow \;\frac{{AN'}}{{AC}} = \frac{{AM}}{{AB}}\)
از مقایسهٔ این تناسب، با فرض مسئله نتیجه می شود \(\frac{{AN'}}{{AC}} = \frac{{AN}}{{AC}}\) و در نتیجه: AN’=AN و بنابراین N بر N’ منطبق است و MN همان MN’ است که موازی BC است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















