1736019749.png)
گام به گام تمرین صفحه 36 درس 2 هندسه دهم (قضیۀ تالس، تشابه و کاربردهای آن)
تعداد بازدید : 61.02Mپاسخ تمرین صفحه 36 هندسه دهم
-گام به گام تمرین صفحه 36 درس قضیۀ تالس، تشابه و کاربردهای آن
-تمرین صفحه 36 درس 2
-1 در شکل مقابل پاره خط MN موازی با BC رسم شده است. درستی و نادرستی هر عبارت را مشخص کنید:
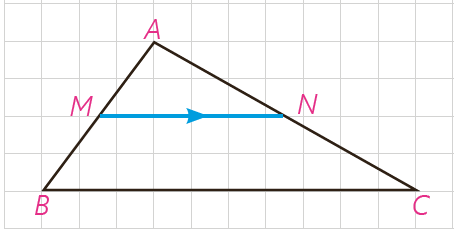
الف \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}} = \frac{{MN}}{{BC}}\)
ب \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\)
پ \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\)
ت \(\frac{{AM}}{{BM}} = \frac{{MN}}{{BC}}\)
ث \(\frac{{MB}}{{AB}} = \frac{{NC}}{{CA}} = \frac{{MN}}{{BC}}\)
ج \(\frac{{MB}}{{MA}} = \frac{{NC}}{{NA}}\)
چ \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\)
ح \(\frac{{MB}}{{AB}} = \frac{{MN}}{{BC}}\)
الف \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}} = \frac{{MN}}{{BC}}\)
نادرست
ب \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\)
درست
پ \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\)
درست
ت \(\frac{{AM}}{{BM}} = \frac{{MN}}{{BC}}\)
نادرست
ث \(\frac{{MB}}{{AB}} = \frac{{NC}}{{CA}} = \frac{{MN}}{{BC}}\)
نادرست
ج \(\frac{{MB}}{{MA}} = \frac{{NC}}{{NA}}\)
درست
چ \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\)
درست
ح \(\frac{{MB}}{{AB}} = \frac{{MN}}{{BC}}\)
نادرست
2 در شکل مقابل DE||BC، باتوجه به اندازه پاره خط ها، طول های DE و AB را به دست آورید.
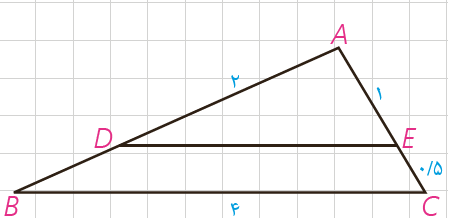
\(\frac{{AD}}{{AB}} = \frac{{DE}}{{BC}} = \frac{{AE}}{{AC}} \Rightarrow \frac{2}{{AB}} = \frac{{DE}}{4} = \frac{1}{{1/5}}\)
\(\Rightarrow \left\{ \begin{array}{l}AB = 3\\DE = \frac{8}{3}\end{array} \right.\)
3 در شکل مقابل MN||BC؛ مقادیر x و y را به دست آورید.
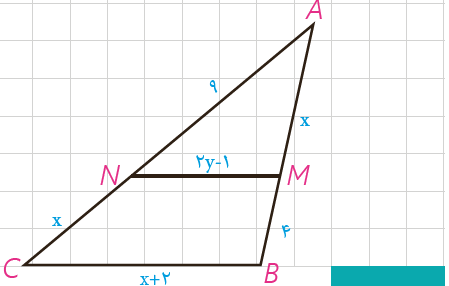
\(\frac{9}{{9 + x}} = \frac{x}{{x + 4}} = \frac{{2y - 1}}{{x + 2}} \Rightarrow \frac{9}{{9 + x}} = \frac{x}{{x + 4}}\)
\(\Rightarrow 9x + 36 = 9x + {x^2} \Rightarrow {x^2} = 36 \Rightarrow x = 6\)
\(\frac{x}{{x + 4}} = \frac{{2y - 1}}{{x + 2}} \Rightarrow \frac{6}{{10}} = \frac{{2y - 1}}{8}\)
\(\Rightarrow 2y - 1 = \frac{{24}}{5} \Rightarrow y = \frac{{29}}{{10}}\)
4 در شکل مقابل می دانیم 'AB=A'B و 'BC||B'C با استفاده از قضیهٔ تالس و عکس آن ثابت کنید: 'AC||A'C
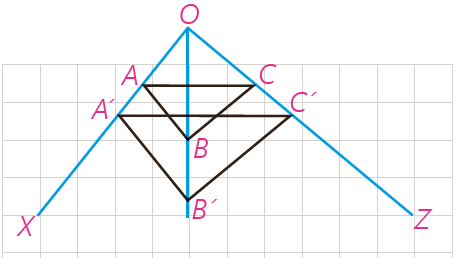
\(\left\{ \begin{array}{l}\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}}\\\frac{{OC}}{{OC'}} = \frac{{OB}}{{OB'}}\end{array} \right. \Rightarrow \frac{{OA}}{{OA'}} = \frac{{OC}}{{OC'}}\)
(عکس قضیه تالس) \(\Rightarrow AC\parallel A'C'\)
5 در شکل مقابل می دانیم BC||DE و BE||DF، به کمک قضیهٔ تالس در مثلث های ADE و ADF و مقایسهٔ تناسب ها با یکدیگر، ثابت کنید: AE2=AC.AF (به عبارت دیگر AE واسطه هندسی بین AC و AF است)
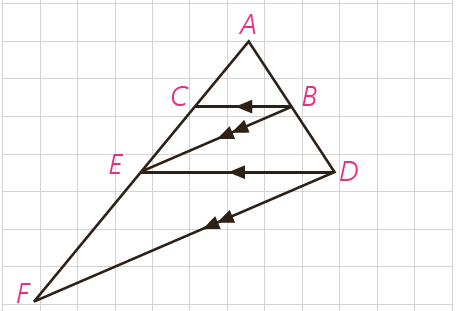
\(\left\{ \begin{array}{l}\frac{{AB}}{{AD}} = \frac{{AC}}{{AE}}\\\frac{{AB}}{{AD}} = \frac{{AE}}{{AF}}\end{array} \right. \Rightarrow A{E^2} = AC.AF\)
6 کی ازکاربردهای قضیهٔ تالس از زمان های دور تاکنون، محاسبهٔ فاصله های غیرقابل دسترس بوده است؛ به عنوان مثال برای تعیین یک ارتفاع بلند مانند ارتفاع یک درخت بلند در زمانی معین، طول سایهٔ درخت را روی زمین اندازه می گیریم؛ سپس یک قطعه چوب کوتاه را که به آن شاخص می گویند، طوری به صورت عمودی جابه جا می کنیم که سایهٔ آن روی امتداد سایهٔ درخت قرار گیرد و نوک سایهٔ شاخص نیز بر نوک سایهٔ درخت منطبق شود؛ به طور مثال اگر طول سایهٔ درخت 60 متر، طول سایهٔ شاخص 3 متر و طول شاخص 1 متر باشد، بلندی درخت چند متر است؟
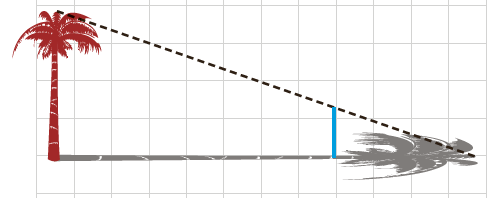
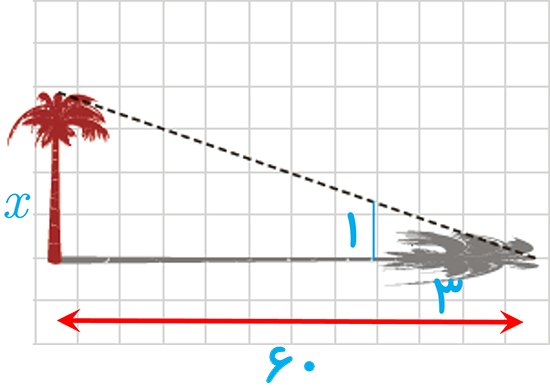
\(\frac{3}{{60}} = \frac{1}{x} \Rightarrow x = \frac{{60}}{3} = 20\)
7 در ذوزنقه مقابل MN||AB||CD، ثابت کنید:
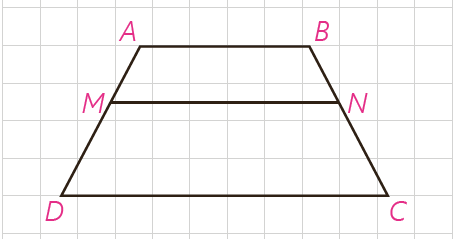
(قضیۀ تالس در ذوزنقه) \(\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}\)
(راهنمایی: یکی از قطرها را رسم کنید.)
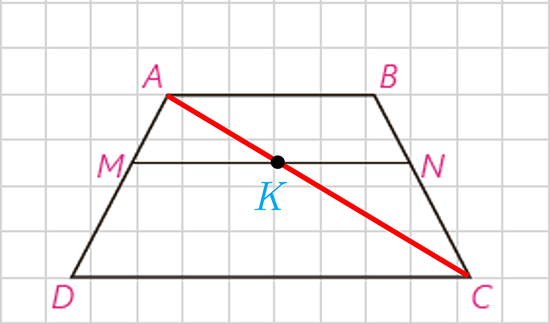
\(\left\{ \begin{array}{l}\frac{{AM}}{{MD}} = \frac{{AK}}{{KC}}\\\frac{{BN}}{{NC}} = \frac{{AK}}{{KC}}\end{array} \right. \Rightarrow \frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}\)
8 ابعاد یک زمین استاندارد والیبال 9 متر در 18 متر است که توسط خط میانی به دو مربع 9×9 تفکیک می شود و تور والیبال مردان با ارتفاع 2/43 متر روی خط وسط نصب شده است. یک بازیکن با قد 180 سانت یمتر و در فاصلهٔ دو متری تور، به هوا می پرد و توپی را که در ارتفاع 30 سانتی متری بالای سرش است با ضربه آبشار مماس بر تور وسط روانه زمین حریف می کند و توپ روی خط انتهای زمین حریف می نشیند. این بازیکن برای ضربه زدن چقدر به هوا پریده است؟
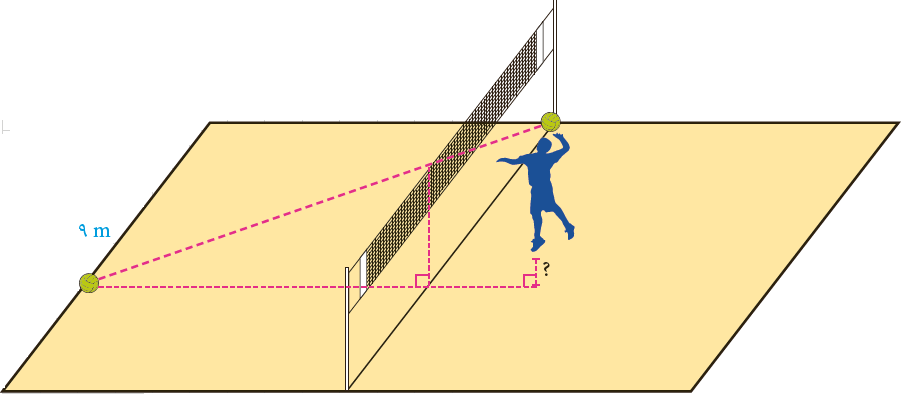
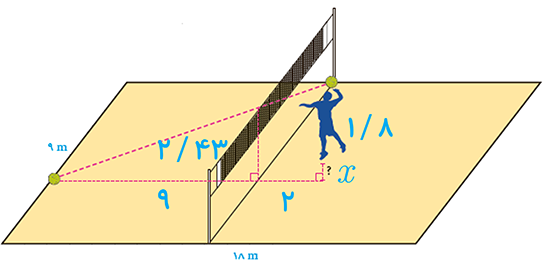
\(\frac{9}{{9 + 2}} = \frac{{2/43}}{{x + 1/8 + 0/3}} \Rightarrow \frac{9}{{11}} = \frac{{2/43}}{{x + 2/1}}\)
\(\Rightarrow 9x + 18/9 = 26/73 \Rightarrow x = 0/87\)
بازیکن 87 سانتی متر به هوا پریده است.
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
