1736019749.png)
گام به گام سؤال متن صفحه 45 درس 2 هندسه دهم (قضیۀ تالس، تشابه و کاربردهای آن)
تعداد بازدید : 62.9Mپاسخ سؤال متن صفحه 45 هندسه دهم
-گام به گام سؤال متن صفحه 45 درس قضیۀ تالس، تشابه و کاربردهای آن
-سؤال متن صفحه 45 درس 2
-اثبات: اگر درستی حکم را برای یکی از ارتفاع ها (میانه ها، نیمسازها) ثابت کنیم، درستی آن قابل تعمیم به سایر ارتفاع ها (میانه ها، نیمسازها) است. (چرا؟)
الف ارتفاع ها
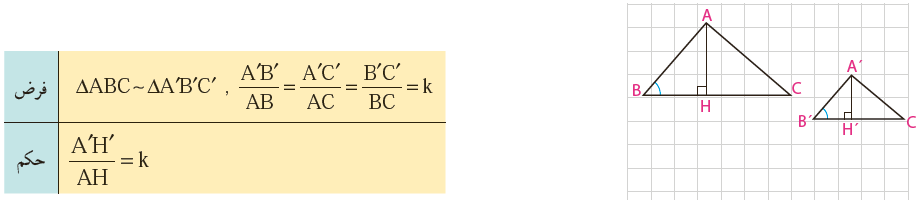
چرا \( \angle B = \angle B'\) بنابراین: \(\Delta ABC \sim \Delta A'B'H'\) (چرا؟) از آنجا درستی حکم را نتیجه گیری کنید.
ب میانه ها
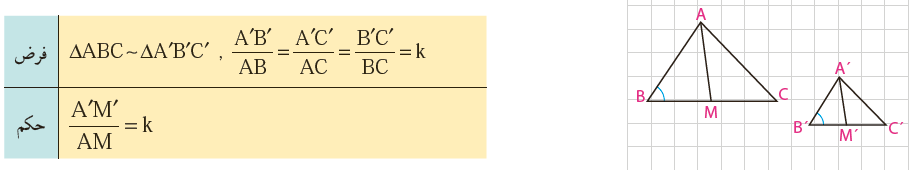
چرا \(\angle B = \angle B'\)؟
\(\frac{{B'M'}}{{BM}} = \frac{{\frac{1}{2}}}{{\frac{1}{2}}} = \frac{{\,\,\,\,\,}}{{}} = k{\mkern 1mu} \Rightarrow {\mkern 1mu} \frac{{A'B'}}{{AB}} = \frac{{B'M'}}{{BM}}\)
بنراین \(\Delta A'B'M' = \Delta ABM\) (چرا؟) از آنجا درستی حکم را نتیجه بگیرید.
ج نیمسازها
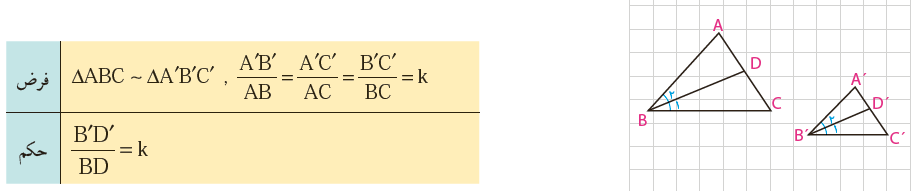
چرا \(\angle A = \angle A'\)، چرا \(\angle {B_1} = \angle {B_1}'\) ؟
بنابراین \(\Delta A'B'D' = \Delta ABD\) (چرا؟) از آنجا درستی حکم را نشان دهید.
الف
زیرا:
\(\begin{array}{l}A\mathop B\limits^\Delta C \sim A'\mathop {B'}\limits^\Delta C' \Rightarrow \left. {\begin{array}{*{20}{l}}{\widehat B = \widehat B'}\\{\widehat H = \widehat H' = 90^\circ }\end{array}} \right\}\\\\ \Rightarrow A\mathop B\limits^\Delta H \sim A'\mathop {B'}\limits^\Delta H'\\\\ \Rightarrow \frac{{A'B'}}{{AB}} = \frac{{A'H'}}{{AH}} = k\end{array}\)
ب
زیرا :
\(A\mathop B\limits^\Delta C \sim A'\mathop {B'}\limits^\Delta C' \Rightarrow \widehat B = \widehat {B'}\)
\(\frac{{B'M'}}{{BM}} = \) \(\frac{{\frac{1}{2}B'C'}}{{\frac{1}{2}BC}}\) \(= \frac{{B'C'}}{{BC}} = K\)
بنابر برابری یک زاویه و تناسب اضلاع همان زاویه :
\(A\mathop B\limits^\Delta M \sim A'\mathop {B'}\limits^\Delta M' \Rightarrow \frac{{A'B'}}{{AB}} = \frac{{A'M'}}{{AM}} = k\)
ج
زیرا :
\(\begin{array}{l}A\mathop B\limits^\Delta C \sim A'\mathop {B'}\limits^\Delta C'\\\\ \Rightarrow \left. \begin{array}{l}\widehat A = \widehat {A'}\\\widehat B = \widehat {B'} \Rightarrow \widehat {\frac{B}{2}} = \widehat {\frac{{B'}}{2}} \Rightarrow \widehat {{B_2}} = \widehat {{{B'}_2}}\end{array} \right\}\\\\ \Rightarrow A\mathop B\limits^\Delta D \sim A'\mathop {B'}\limits^\Delta D'\\\\ \Rightarrow \frac{{A'B'}}{{AB}} = \frac{{A'D'}}{{AD}} = k\end{array}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه
همین حالا نصب کن
