جواب تمرین صفحه 42 درس 2 هندسه دهم (قضیۀ تالس، تشابه و کاربردهای آن)
تعداد بازدید : 81.09Mپاسخ تمرین صفحه 42 هندسه دهم
-گام به گام تمرین صفحه 42 درس قضیۀ تالس، تشابه و کاربردهای آن
-تمرین صفحه 42 درس 2
-شما در حال مشاهده جواب تمرین صفحه 42 هندسه دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 در هر یک از شکل های زیر، تشابه مثلث ها را ثابت کنید و از آنجا مقادیر y ، x را مشخص کنید:
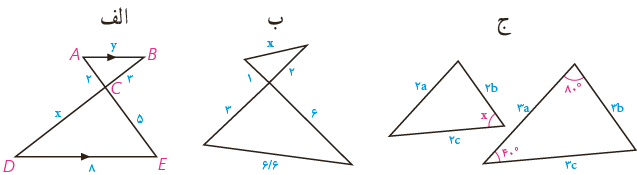
الف
تساوی هر سه زاویه (دو به دو با هم)
\(\frac{x}{3} = \frac{5}{2} = \frac{8}{y} \Rightarrow x = \frac{{15}}{2} \Rightarrow y = \frac{{16}}{5}\)
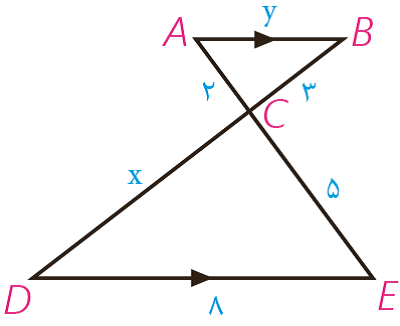
ب
تناسب دوضلع با نسبت تناسب: \(\frac{1}{2}\) و برابری زاویه بین
\(\frac{x}{{6/6}} = \frac{2}{6} = \frac{1}{3} \Rightarrow x = 3/3\)
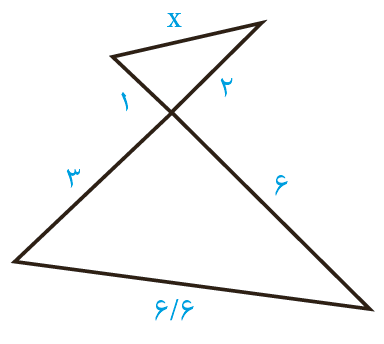
ج
تناسب هر سه ضلع با نسبت تناسب:
\(x = {180^\circ } - \left( {{{40}^\circ } + {{80}^\circ }} \right) = {60^\circ }\)
2 در مثلث قائم الزاویهٔ ABC \(\left( {\widehat A = {{90}^\circ }} \right)\) ارتفاع AH را رسم کرده ایم. به کمک روابط طولی در مثلث قائم الزاویه در هر یک از موارد زیر با توجه به مفروضات داده شده، مقادیر مجهول را محاسبه کنید.
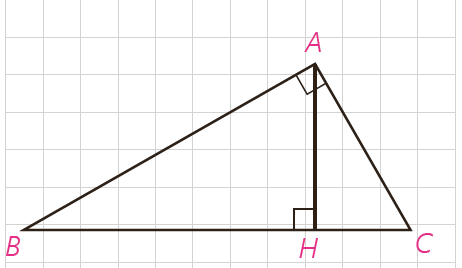
1 BH=9 , CH=4 , AH=? , AB=? , AC=?
2 AB=8 , AC=6 , BH=? , CH=?
1 \(\frac{{BH}}{{AH}} = \frac{{AH}}{{CH}} \Rightarrow \frac{9}{{AH}} = \frac{{AH}}{4}\)
\( \Rightarrow A{H^2} = 9 \times 4 = 36 \Rightarrow AH = 6\)
\(AB = \sqrt {B{H^2} + A{H^2}} = \sqrt {{9^2} + {6^2}} = 3\sqrt {13}\)
\(AC = \sqrt {B{H^2} + A{H^2}} = \sqrt {{4^2} + {6^2}} = 2\sqrt {13}\)
2 \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{8^2} + {6^2}} = 10\)
\(\Rightarrow \frac{1}{2}AH \times 10 = \frac{1}{2} \times 8 \times 6 \Rightarrow AH = \frac{{24}}{5}\)
\(\frac{{BH}}{{AH}} = \frac{{AB}}{{AC}} \Rightarrow \frac{{BH}}{{\frac{{24}}{5}}} = \frac{8}{6} \Rightarrow BH = \frac{{32}}{5} = 6/4\)
\(CH = BC - BH = 10 - 6/4 = 3/2\)
3 در شکل روبه رو \(\angle {A_1} = \angle B\) و AC=4 و BD=6، طول BC را به دست آورید.
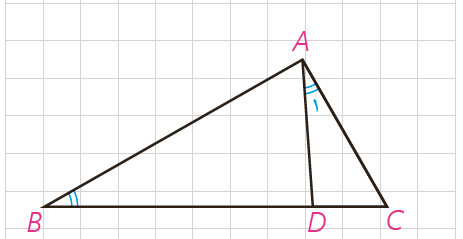
\(\widehat B = \widehat {{A_1}}\) , \(\widehat C =\) مشترک
\(\Rightarrow A\mathop B\limits^\Delta C \sim A\mathop D\limits^\Delta C \Rightarrow \frac{{DC}}{{AC}} = \frac{{AC}}{{BC}} = \frac{{AD}}{{AB}} \)
\(\Rightarrow A{C^2} = DC \cdot BC\)
\(\Rightarrow {4^2} = \left( {BC - BD} \right)BC \)
\(\Rightarrow 16 = \left( {BC - 6} \right)BC \Rightarrow BC = 8\)
4 در شکل مقابل، مثلثی با اضلاع 13 و 14 و 15 رسم شده است. به کمک قضیهٔ فیثاغورس در مثلث های ABH و ACH، مقادیر x و y را به دست آورید و از آنجا مساحت مثلث را محاسبه کنید.
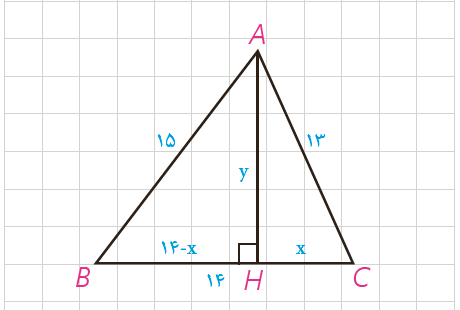
\(\left. \begin{array}{l}{15^2} = {\left( {14 - x} \right)^2} + {y^2} = 225\\{13^2} = {x^2} + {y^2} = 169\end{array} \right\}\)
\( \Rightarrow 225 - {\left( {14 - x} \right)^2} = 169 - {x^2}\)
\(\Rightarrow 225 - 196 - {x^2} + 28x = 169 - {x^2}\)
\(\Rightarrow 28x = 140 \Rightarrow x = 5\)
\(\Rightarrow {y^2} = 169 - {x^2} = 169 - 25 = 144 \Rightarrow y = 12\)
5 در حیاط یک دبیرستان، دو درخت بلند وجود دارد. معلم هندسه از دانش آموزان خواست که برای تعیین ارتفاع این دو درخت روشی را ارائه کنند. در اینجا روش های دو دانش آموز را می بینید. با توجّه به اطلاعات داده شده ارتفاع هر درخت را تعیین کنید.
الف روش ترانه: ترانه یک چوب 2/5 متری را به صورت عمودی روی زمین در جایی محکم کرد. طول سایهٔ چوب در آن زمان 1/5 متر بود. هم زمان طول سایهٔ درخت 2 متر بود. با توجه به شکل ارتفاع این درخت چند متر است؟
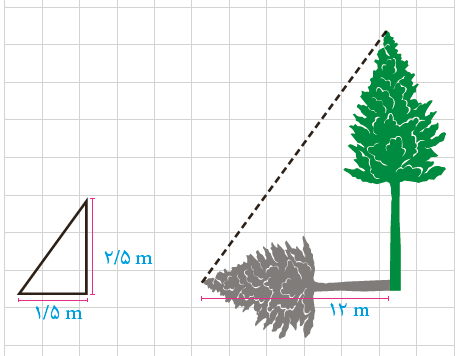
ب روش شهرزاد: شهرزاد آینه ای کوچک را که در مقیاس بزرگ می توان یک نقطه در نظر گرفت، (نقطۀ O در شکل) روی زمین و در مسیر خط راستی که از پای درخت تا پای خودش کشیده است، قرار داد؛ سپس روی این خط آنقدر به جلو و عقب حرکت کرد تا بتواند، تصویر نوک درخت را در آینه ببیند. با توجّه به آنچه از خواص آینه ها و انعکاس نور می دانید، بگویید چگونه می توان با داشتن طول های AO و BO روی زمین و اندازهٔ قد شهرزاد (فاصله چشم او تا زمین)، ارتفاع درخت را به دست آورد. اگر قد شهرزاد 160 سانتی متر و فاصلهٔ پای او از آینه 2/5 متر و فاصلهٔ آینه از پای درخت 20 متر باشد، ارتفاع درخت چند متر است؟
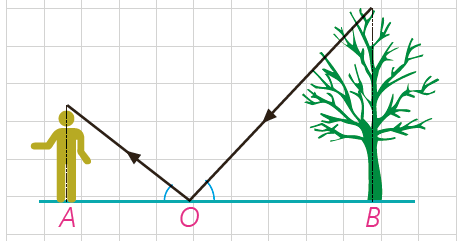
الف
\(\frac{h}{{2/5}} = \frac{{12}}{{1/5}} \Rightarrow h = 20\)
ب
\(\frac{h}{{1/6}} = \frac{{20}}{{2/5}} \Rightarrow h = 12/8\)
6 با قضیه فیثاغورس آشنا شدید. این قضیه می گوید اگر زاویهٔ A از مثلثی مانند ABC، قائمه باشد، آنگاه a2=b2+c2
الف عکس این قضیه را بنویسید.
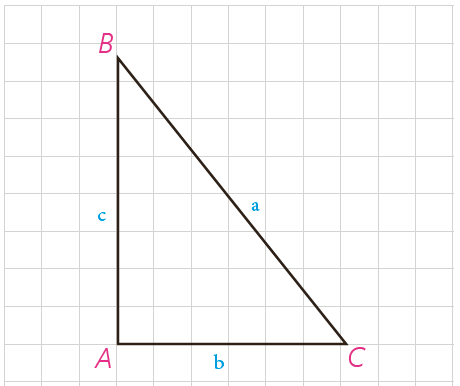
ب با انجام دادن مراحل زیر نتیجه بگیرید که عکس قضیه فیثاغورس نیز درست است.
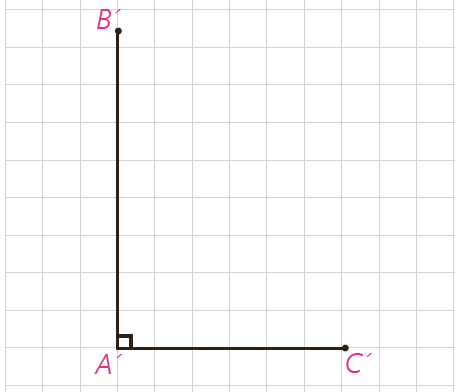
1) فرض کنیم مثلث ABC داده شده است و رابطهٔ a2=b2+c2 بین اندازهٔ طول های اضلاع آن برقرار است.
2) پاره خط های 'A'B و 'A'C را مطابق شکل مقابل به گونه ای درنظر بگیرید که A'=90° و A'C'=AC و A'B'=AB
3) با استفاده از قضیه فیثاغورس در مثلث 'A'B'C اندازۀ پاره خط 'B'C را به دست آورید و ثابت کنید B'C'=BC
4) توضیح دهید چرا 'ABC=A'B'C و نتیجه بگیرید A=90°
ج قضیه فیثاغورس و عکس آن را به صورت یک قضیهٔ دو شرطی بیان نمایید.
الف
اگر در مثلث ABC رابطه \({a^2} = {b^2} + {c^2}\) برقرار باشد، آن گاه زاویه A قائمه خواهد بود.
ب
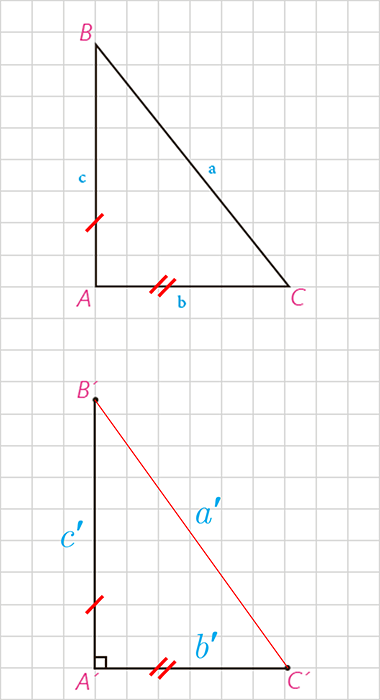
طبق فرض: \({a^2} = {b^2} + {c^2}\)
\(\widehat {A'} = {90^ \circ } \Rightarrow \left\{ \begin{array}{l}{{a'}^2} = {{b'}^2} + {{c'}^2} = {b^2} + {c^2} = {a^2} \Rightarrow a' = a\\b' = b\\c' = c\end{array} \right.\)
\(\Rightarrow\) بنا به حالت (ض ض ض)
\(\Rightarrow A\mathop B\limits^\Delta C \cong A'\mathop {B'}\limits^\Delta C' \Rightarrow \widehat A = \widehat {A'} = {90^ \circ }\)
ج اگر در مثلث ABC ،زاویه A قائمه باشد، آنگاه رابطه \({a^2} = {b^2} + {c^2}\) برقرار است و برعکس .
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















