جواب تمرین صفحه 48 درس 2 هندسه دهم (قضیۀ تالس، تشابه و کاربردهای آن)
تعداد بازدید : 80.73Mپاسخ تمرین صفحه 48 هندسه دهم
-گام به گام تمرین صفحه 48 درس قضیۀ تالس، تشابه و کاربردهای آن
-تمرین صفحه 48 درس 2
-شما در حال مشاهده جواب تمرین صفحه 48 هندسه دهم هستید. ما در تیم مای درس، پاسخنامههای کاملاً تشریحی و استاندارد را مطابق با آخرین تغییرات کتاب درسی 1404 برای شما گردآوری کردهایم. اگر به دنبال بهروزترین پاسخها برای این صفحه هستید و میخواهید بدون نیاز به اتصال به اینترنت، علاوه بر پاسخهای گام به گام، به گنجینهای از مطالب درسی دسترسی پیدا کنید، حتماً اپلیکیشن مایدرس را نصب نمایید.
📥 دانلود اپلیکیشن مایدرس
برای دسترسی آفلاین، سریع و بدون نیاز به اینترنت به گنجینهای از گامبهگامها و نمونه سوالات، اپلیکیشن را نصب کنید.
1 طول های اضلاع یک مثلث 10 و 12 و 15 سانتی متر است و طول بلندترین ضلع مثلثی متشابه آن، 10 سانتی متر است. محیط مثلث دوم را به دست آورید.
\(k = \frac{{15}}{{10}} = \frac{P}{{P'}} = \frac{3}{2} \)
\(\Rightarrow P = 15 + 12 + 10 = 37 \)
\(\Rightarrow \frac{{37}}{{P'}} = \frac{3}{2} \Rightarrow P' = \frac{{74}}{3}\)
2 در شکل روبه رو BC||MN است و مساحت ذوزنقهٔ MNCB هشت برابر مساحت مثلث AMN است. نسبت \(\frac{{MB}}{{MA}}\) را به دست آورید.
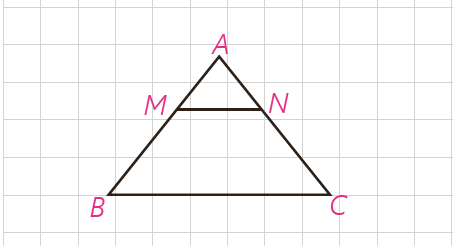
\(\frac{{{S_{MNCB}}}}{{{S_{AMN}}}} = \frac{8}{1} \Rightarrow \frac{{{S_{MNCB}} + {S_{AMN}}}}{{{S_{AMN}}}} = \frac{{8 + 1}}{1} \)
\(\Rightarrow \frac{{{S_{ABC}}}}{{{S_{AMN}}}} = 9 = {k^2}\)
\(\Rightarrow k = 3 = \frac{{AB}}{{MA}} \Rightarrow \frac{{MB}}{{MA}} = \frac{{AB - MA}}{{MA}} = \frac{{3 - 1}}{1} \)
\(\Rightarrow \frac{{MB}}{{MA}} = 2\)
3 در شکل روبه رو می دانیم BE=2DE است. اولاً x و y را به دست آورید. ثانیاً نسبت مساحت مثلث BCD به مساحت ABE را بیابید.
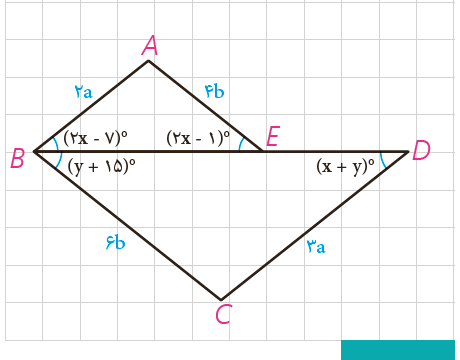
\(\frac{{AB}}{{CD}} = \frac{{AE}}{{BC}} = \frac{{BE}}{{BD}} \)
\(\Rightarrow \left\{ \begin{array}{l}2x - 7 = x + y \Rightarrow x - y = 7\\2x - 1 = y + 15 \Rightarrow 2x - y = 16\end{array} \right. \)
\(\Rightarrow \left\{ \begin{array}{l}x = 9\\y = 2\end{array} \right.\)
\(\frac{{{S_{BCD}}}}{{{S_{ABE}}}} = {\left( {\frac{{BD}}{{DE}}} \right)^2} = {\left( {\frac{{BE + DE}}{{DE}}} \right)^2} \)
\(= {\left( {\frac{{BE}}{{DE}} + 1} \right)^2} = {\left( {2 + 1} \right)^2} = {3^2} = 9\)
4- در مثلث قائم الزاویهٔ ABC \(\left( {\widehat A = {{90}^\circ }} \right)\) ارتفاع AH را رسم می کنیم. می دانید که \(\Delta ABH \sim \Delta ABC \sim \Delta ACH\) است. با توجّه به این موضوع،
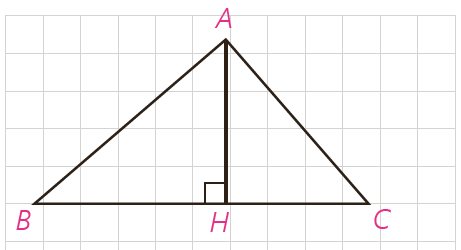
الف ثایت کنید:
\(\frac{{{S_{ABH}}}}{{{S_{ABC}}}} = {\left( {\frac{{AB}}{{BC}}} \right)^2}\;\;,\;\;\frac{{{S_{ACH}}}}{{{S_{ABC}}}} = {\left( {\frac{{AC}}{{BC}}} \right)^2}\)
ب با جمع کردن دو طرف تساوی های بالا و ادامهٔ کار، درستی قضیهٔ فیثاغورس را نتیجه گیری کنید.
الف
\(\frac{{{S_{ABH}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}AH \cdot BH}}{{\frac{1}{2}AB \cdot AC}} = \frac{{AH \cdot BH}}{{AB \cdot AC}} = \frac{{BH}}{{AB}} \times \frac{{AH}}{{AC}} \)
\(= \frac{{AB}}{{BC}} \times \frac{{AB}}{{BC}} = {\left( {\frac{{AB}}{{BC}}} \right)^2}\)
\(\frac{{{S_{ACH}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}AH \cdot CH}}{{\frac{1}{2}AB \cdot AC}} = \frac{{AH \cdot CH}}{{AB \cdot AC}} = \frac{{AH}}{{AB}} \times \frac{{CH}}{{AC}} \)
\(= \frac{{AC}}{{BC}} \times \frac{{AC}}{{BC}} = {\left( {\frac{{AC}}{{BC}}} \right)^2}\)
ب
\(\frac{{{S_{ABH}}}}{{{S_{ABC}}}} + \frac{{{S_{ACH}}}}{{{S_{ABC}}}} = \frac{{{S_{ABH}} + {S_{ACH}}}}{{{S_{ABC}}}} = \frac{{{S_{ABC}}}}{{{S_{ABC}}}} \)
\(= {\left( {\frac{{AB}}{{BC}}} \right)^2} + {\left( {\frac{{AC}}{{BC}}} \right)^2} = \frac{{A{B^2} + A{C^2}}}{{B{C^2}}}\)
\(\Rightarrow 1 = \frac{{A{B^2} + A{C^2}}}{{B{C^2}}} \Rightarrow B{C^2} = A{B^2} + A{C^2}\)
5 مطابق شکل، روی یک ساختمان، یک آنتن به ارتفاع 3/2 متر نصب شد ه است. در فاصله 60 متری ساختمان، یک تیر برق 6 متری قائم وجود دارد و یک ناظر وقتی در فاصله 20 متری تیر م یایستد، انتهای آنتن و انتهای تیر برق را در یک راستا می بیند. اگر بدانیم فاصلهٔ چشمان ناظر از زمین 1/6 متر است، بلندی ساختمان را محاسبه کنید.
(از چشم ناظر خط راستی موازی زمین رسم کنید تا تیر برق و ساختمان را قطع کند. از قضیۀ تالس کمک بگیرید.)
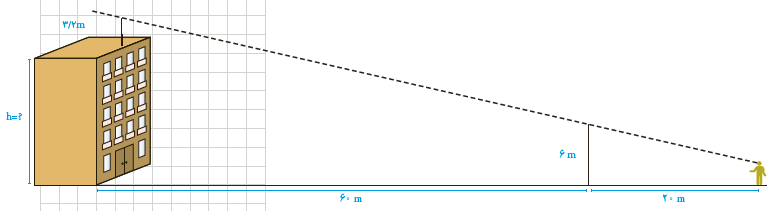
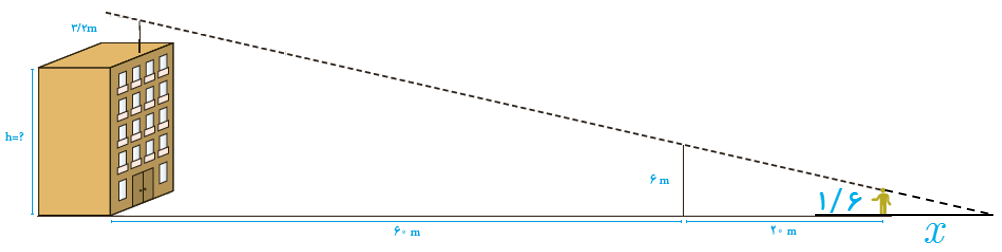
\(\frac{x}{{1/6}} = \frac{{20 + x}}{6} \Rightarrow 6x = 32 + 1/6x\)
\( \Rightarrow 4/4x = 32 \Rightarrow x = \frac{{32}}{{4/4}} = \frac{{80}}{{11}}\)
\(\frac{x}{{1/6}} = \frac{{80 + x}}{{h + 3/2}} \Rightarrow h.x + 3/2x = 128 + 1/6x \)
\(\Rightarrow h = \frac{{128 - 1/6x}}{x} = \frac{{128}}{x} - 1/6\)
\(h = \frac{{128}}{{\frac{{80}}{{11}}}} - 1/6 = 17/6 - 1/6 = 16\)
6 در دوربی نهای قدیمی، موقع عکس برداری، روی یک حلقهٔ فیلم تعداد محدودی (مثلاً سی و شش عدد) تصویر منفی ثبت، و سپس این فیلم ظاهر می شود و عکس ها از روی آن چاپ می شوند. اگر فرض کنیم عرض یکی از این فیلم ها، 35mm و فاصلهٔ آن درون دوربین تا عدسی، 4/2cm و فاصله عدسی تا درختی که از آن عکس می گیرد، 6m باشد، اندازهٔ واقعی درختی که از آن عکس گرفته می شود، چند متر است؟
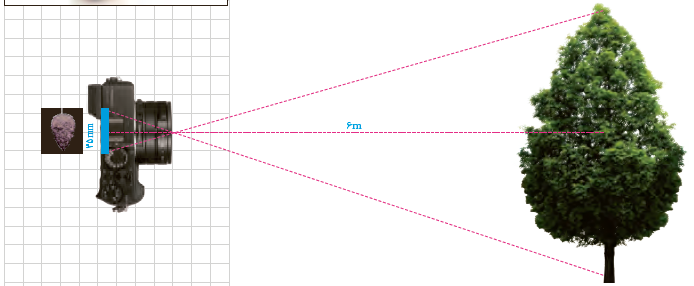
\(\frac{{3/{5^{cm}}}}{{4/{2^{cm}}}} = \frac{{{h^m}}}{{{6^m}}} \Rightarrow h = \frac{{3/5 \times 6}}{{4/2}} = {5^m}\)
مای درس ، برترین اپلیکیشن کمک درسی ایران
پوشش تمام محتواهای درسی پایه چهارم تا دوازدهم- آزمون آنلاین تمامی دروس
- گام به گام تمامی دروس
- ویدئو های آموزشی تمامی دروس
- گنجینه ای از جزوات و نمونه سوالات تمامی دروس
- فلش کارت های آماده دروس
- گنجینه ای جامع از انشاء های آماده
- آموزش جامع آرایه های ادبی، دستور زبان، قواعد زبان انگلیسی و ... ویژه



1736019749.png)















