جواب تمرین های ترکیبی صفحه 124 درس 9 ریاضی هفتم (آمار و احتمال)

1 آمار

علمی است که در آن اطلاعات خاصی را جمع آوری سازماندهی و بررسی میکنند به عنوان مثال، سرشماری کشور که خود نوعی آمارگیری و جمع آوری اطلاعات از کل خانوارهای کشور است.

2 جمع آوری داده

عملی است که اطلاعات خاصی را از گروه یا جامعه مورد مطالعه بدست میآید را جمع آوری داده گویند. مانند عملی که سرشماران در هر سرشماری انجام می دهند.

3 نمونه گیری

عملی است که بوسیله آن از چند جامعه که دارای نمونههای زیادی هستند چند نمونه را انتخاب کنند و اطلاعات را از آن چند نمونه بدست آورند و بر اساس همان اطلاعات آن چند جامعه را با هم مورد مقایسه قرار دهند. به عنوان مثال از چند شغل مختلف که افراد زیادی را شامل میشوند چند نفر را از هر شغل انتخاب کرده و درآمد کسب شده از آن شغل ها را با هم مقایسه کنند.

4 اتفاق های هم شانس

اتفاق هایی که میزان احتمال رخ دادن آن با هم برابر باشند. مثلا در پرتاب یک سکه احتمال اینکه سکه رو بیاید و یا پشت بیاید هم شانس هستند.

5 احتمال

میزان شانس رخ دادن یک اتفاق در برابر کل اتفاقهایی که ممکن است در یک آزمایش خاص رخ دهد که عددی است همواره بین صفر تا یک به عنوان مثال احتمال رو آمدن سکه در یک پرتاب برابر باد است.

1 سازماندهی داده ها در جدول

سازماندهی داده ها در جدول جمع بندی و طبقه بندی اطلاعاتی خاص که یک یا چند ویژگی خاص آنها با هم مقایسه می شوند. به عنوان مثال اطلاعات جمع آوری شده از جواد در مثال اول همین درس:

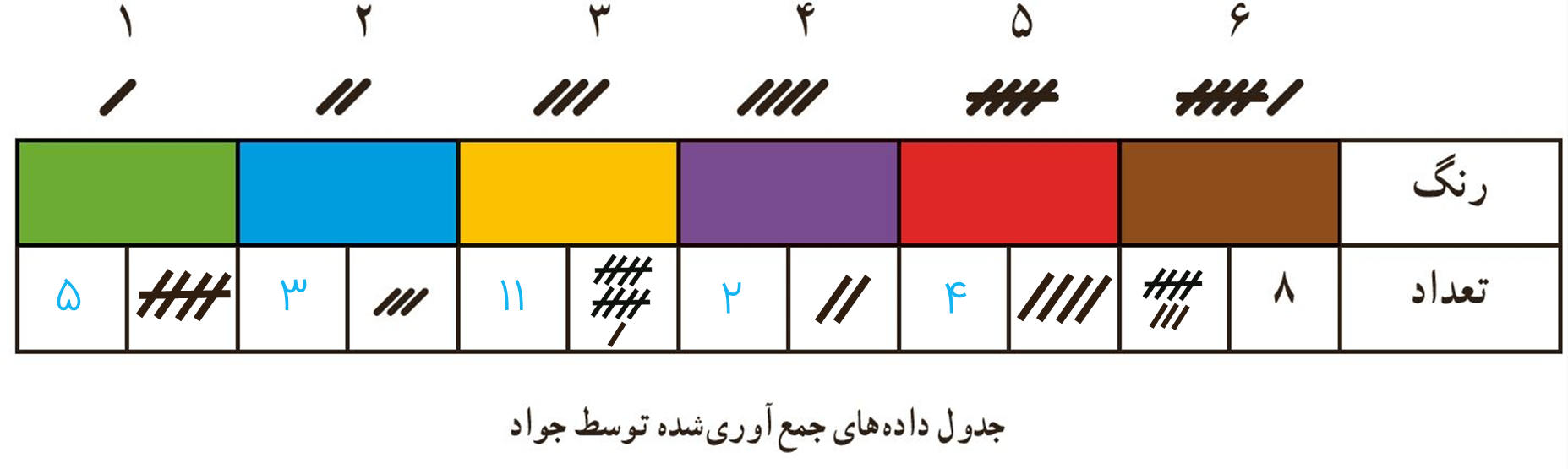
2 رسم نمودار ستونی

صورتی از نمایش اطلاعات طبقه بندی شده که یک یا چند ویژگی خاص آنها با هم مقایسه می شوند. به عنوان مثال اطلاعات جمع آوری شده از محمد در مثال اول همین درس:

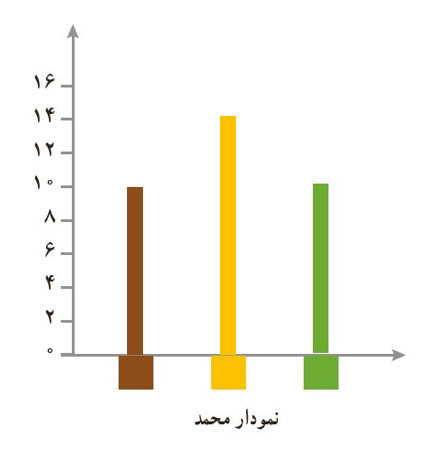
3 رسم نمودار خط شکسته

صورت دیگری از نمایش اطلاعات طبقه بندی شده که یک یا چند ویژگی خاص آنها با هم مقایسه می شوند که به وسیله نقطه و خط رسم میشود به عنوان مثال نمودار زیر میزان تغییرات میانگین دمای ماهانه یزد در ۱۲ ماه سال است:

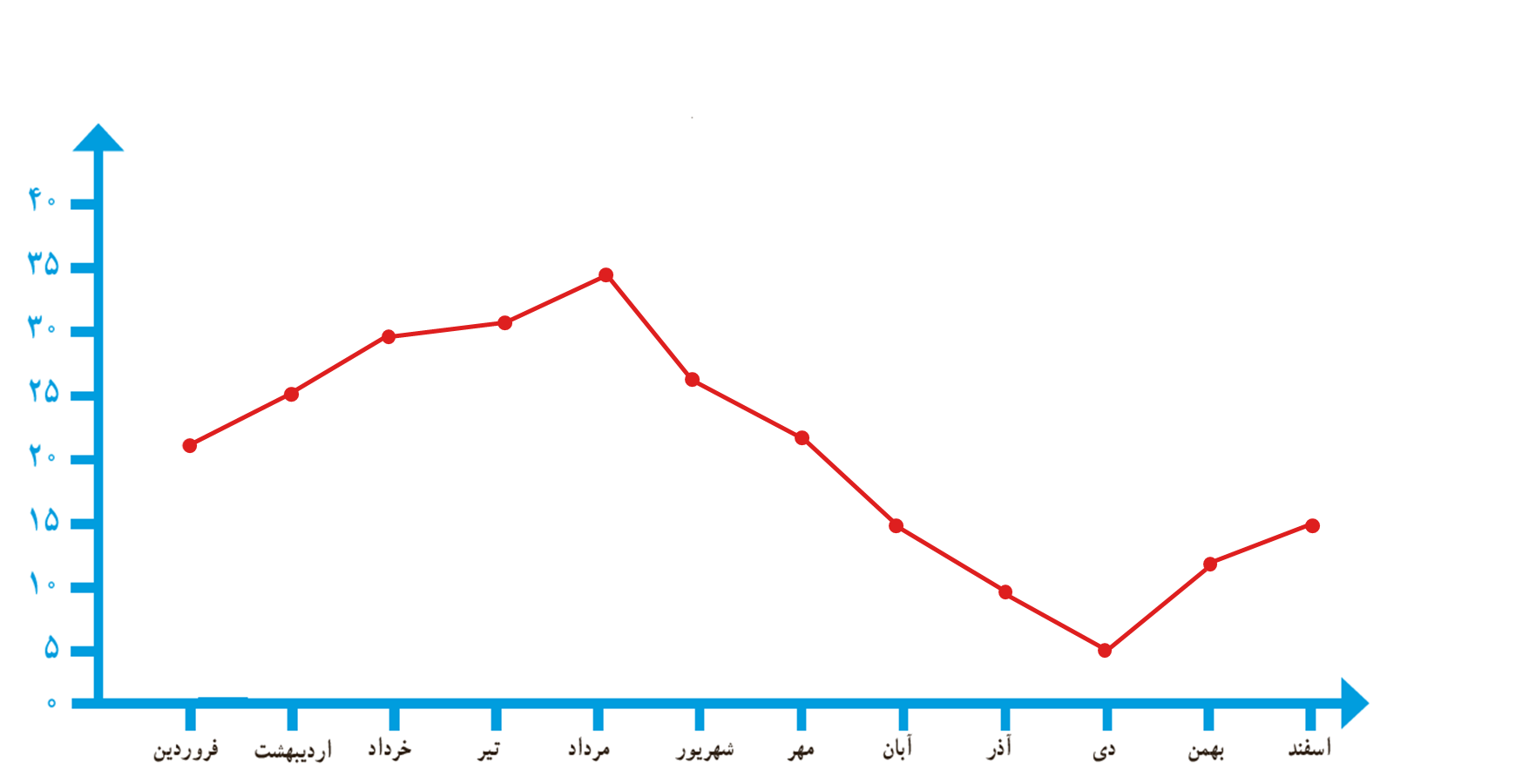
4 رسم نمودار تصویری

صورت دیگری از نمایش اطلاعات جمع آوری شده است که در این نوع نمودار بعضی از اطلاعات نشان می دهد که یک مقدار مشخص به چه نسبتی به بخشهای کوچکتر تقسیم شده است. در این موارد میتوان تقسیم شدن را روی یک شکل مثلا دایره نشان داد و سهم هر بخش را روی دایره مشخص کرد به عنوان مثال نمودار دایره ای آمار کتابخوانی در مدرسه راهنمایی شهید مؤذن پور به صورت زیر است:

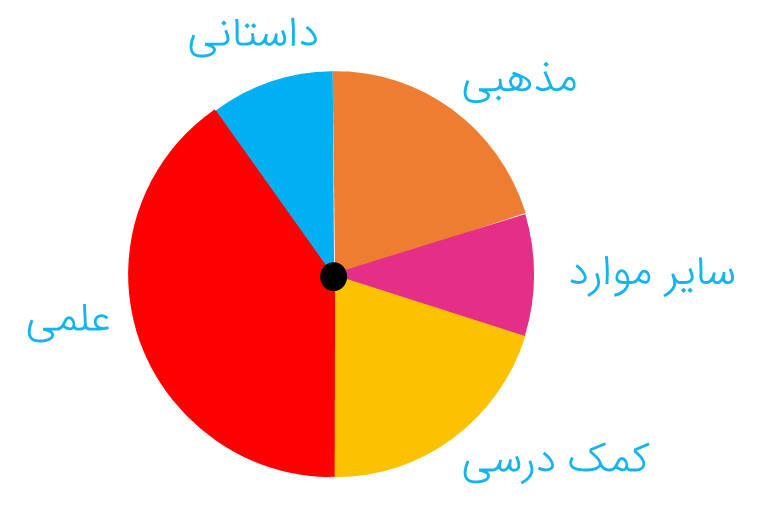
5 کاربرد هر یک از نمودارها در مسائل مختلف

نمودار ستونی برای نمایش بیشترین داده و کمترین داده به کار میرود به عنوان مثال نمودار ستونی بارندگی سالیانه در ماههای مختلف سال.

از نمودار خط شکسته برای نمایش تغییر در بازارهای مالی قیمت طلا ،نفت سهام و ... کاربرد دارد.

از نمودار تصویری برای نمایش نسبت تجمع نسبی داده ها استفاده می کنند به عنوان مثال نمودار دایره ای میزان علایق دانش آموزان به انواع کتاب.

6 انتخاب نمودار مناسب برای موضوع موردنظر

ابتدا هدف از نمایش نمودار را در نظر میگیریم اگر هدف نشان دادن میزان کوچکی و بزرگی میزان داده های آماری باشد از نمودار ستونی استفاده میکنیم اگر هدف نمایش میزان تغییرات دادههای آماری باشد، از نمودار خط شکسته استفاده میکنیم اگر هدف نمایش اطلاعات به صورت کلی باشد از نمودار تصویری استفاده می کنیم.

7 تشخیص حتمی، ممکن یا غیرممکن بودن یک اتفاق

اگر یک اتفاقی را در نظر بگیریم که در همه شرایط مورد نظر همواره اتفاق میافتد این اتفاق برای رخداد بعدی حتمی خواهد بود. اگر گاهی اتفاق میافتد و گاهی اتفاق نمی افتد این اتفاق برای رخداد بعدی ممکن خواهد بود و اگر هرگز اتفاق نمی افتد این اتفاق مورد نظر برای رخداد بعدی غیر ممکن خواهد بود به عنوان مثال کمتر از ۷ ظاهر شدن بر روی تاس بعد از پرتاب اتفاق حتمی خواهد بود اگر عددی زوج ظاهر شود این اتفاق ممکن خواهد بود و اگر بزرگتر از ۷ ظاهر شود این اتفاق غیر ممکن خواهد بود.

8 پیدا کردن احتمال رخ دادن یک اتفاق

برای اینکه احتمال رخ دادن یک اتفاق را بدست آوریم ابتدا همه حالتهای ممکن را می یابیم سپس حالت های مورد نظر را از میان حالتهای ممکن پیدا میکنیم احتمال رخ دادن اتفاق مورد نظر برابر است با نسبت تعداد حالت های مورد نظر به تعداد حالت های ممکن بنابراین احتمال رخ دادن یک احتمال برابر خواهد بود با نسبت تعداد حالت های مطلوب به روی تعداد حالت های ممکن.

به عنوان مثال در ظاهر شدن عدد زوج در پرتاب تاس تعداد حالتهای مطلوب برابر ۳ و تعداد حالت های ممکن برابر ۶ می باشد. در نتیجه احتمال ظاهر شدن عدد زوج در پرتاب تاس برابر \(\frac{1}{2}\) می باشد.

9 آزمایش و ثبت نتایج مربوط به یک اتفاق تصادفی

می خواهیم درستی یا نادرستی یک حتمالی را بررسی کنیم به آزمایش و ثبت نتایج می پردازیم. هر چه تعداد آزمایشها و ثبت نتایجها بیشتر باشد با اطمینان بیشتری میتوانیم بگوییم که این احتمال چقدر به واقعیت نزدیک تر است و یا چقدر از آن دور است. به عنوان مثال جدول زیر که در کار در کلاس کامل شد مربوط می شود به آزمایشهایی که در خارج کردن یک مهره از یک کیسه که درون آن یک مهره قرمز و دو مهره آبی وجود داشت.

10 مقایسهٔ احتمال رخ دادن یک اتفاق با نتایج آزمایش ها

نوبت آزمایش رنگ مهره ق مقایسه احتمال رخ دادن یک اتفاق با نتایج آزمایشها هنگامی که نتایج یک آزمایش به خصوص را ثبت کردیم آن را با میزان احتمال رخ دادن همان اتفاق بررسی می کنیم تا مشاهده کنیم که نتایج عملی چقدر با نتایج نظری بر روی کاغذ مطابقت می.کند هر چه این تطابق نزدیک تر باشد. مقداری که برای احتمال رخ دادن اتفاق بدست آوردیم صحیح تر است و هرچه این تطابق کمتر باشد، نادرستی آن معلوم می شود به عنوان مثال از بررسی آزمایش خارج کردن یک مهره از کیسه حاوی یک مهره قرمز و دو مهره آبی، متوجه شدیم که درستی احتمال چقدر با نتایج آزمایش مطابقت می کند:

\( = \frac{6}{{10}} = \frac{3}{5}\) نتیجه آزمایش خارج شدن مهره آبی                                    \( = \frac{2}{3}\) احتمال خارج شدن مهره آبی

\( = \frac{4}{{10}} = \frac{2}{5}\) نتیجه آزمایش خارج شدن مهره آبی                                   \( = \frac{1}{3}\) احتمال خارج شدن مهره قرمز

1

 \(= \frac{6}{{10}} = \frac{3}{5}\) تعداد اعداد زوج ظاهر شده به کل آزمایش ها

 \( = \frac{3}{6} = \frac{1}{2}\) احتمال عدد زوج ظاهر شدن بعد از پرتاب تاس

3 خیر؛ همیشه این طور نیست.

4 بله؛ امکان دارد برابر باشند.

5 بله؛ هر چقدر تعداد آزمایشها بیشتر شود نتایج بدست آمده با مقدار احتمال برابر می شوند.